The last bit of evidence from physics which I'll discuss is the "no-boundary" proposal of Jim Hartle and Stephen Hawking (and some related ideas). The Hartle-Hawking proposal was described in Hawking's well known pop book, A Brief History of Time. This is an excellent pop description of Science, which also doubles as a somewhat dubious resource for the history of religious cosmology, as for example in this off-handed comment:
[The Ptolemaic Model of Astronomy] was adopted by the Christian church as the picture of the universe that was in accordance with Scripture, for it had the great advantage that it left lots of room outside the sphere of fixed stars for heaven and hell.
![^{[citation\,needed!]}](http://www.wall.org/~aron/blog/wp-content/plugins/latex/cache/tex_5bcaab41e3170d86c9052a23fde1103a.gif)
Carroll, after making some metaphysical comments about how outdated Aristotelian metaphysics is, and how the only things you really need in a physical model are mathematical consistency and fitting the data—this is Carroll's main point, well worthy of discussion, but not the subject of this post—goes on to comment on the Hartle-Hawking state in this way:
Can I build a model where the universe had a beginning but did not have a cause? The answer is yes. It’s been done. Thirty years ago, very famously, Stephen Hawking and Jim Hartle presented the no-boundary quantum cosmology model. The point about this model is not that it’s the right model, I don’t think that we’re anywhere near the right model yet. The point is that it’s completely self-contained. It is an entire history of the universe that does not rely on anything outside. It just is like that.
Temporarily setting aside Carroll's comment that he doesn't actually think this specific model is true—we'll see some possible reasons for this later—the first thing to clear up about this is that the Hartle-Hawking model doesn't actually have a beginning! At least, it probably doesn't have a beginning, not in the traditional sense of the word. To the extent that we can reliably extract predictions from it at all, one typically obtains an eternal universe, something like a de Sitter spacetime. This is an eternal spacetime which contracts down to a minimum size and then expands: as we've already discussed in the context of the Aguirre-Gratton model.
This is because the Hartle-Hawking idea involves performing a "trick", which is often done in mathematical physics, although in this case the physical meaning is not entirely clear. The trick is called Wick rotation, and involves going to imaginary values of the time parameter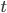 
. The supposed "beginning of time" actually occurs at values of the time parameter that are imaginary! If you only think about values of 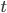which are real, most calculations seem to indicate that with high probability you get a universe which is eternal in both directions.
Now why is the Hartle-Hawking model so revolutionary? In order to make predictions in physics you need to specify two different things: (1) the "initial conditions" for how a particular system (or the universe) starts out at some moment of time, and (2) the "dynamics", i.e. the rule for how the universe changes as time passes.
Most of the time, we try to find beautiful theories concerning (2), but for (1) we often just have to look at the real world. In cosmology, the effective initial conditions we see are fairly simple but have various features which haven't yet been explained. What's interesting about the Hartle-Hawking proposal is that is a rather elegant proposal for (1), the actual initial state of a closed universe.
One reason that the Hartle-Hawking proposal is so elegant is that the rule for the initial condition is, in a certain sense, almost the exact same rule as the rule for the dynamics, except that it uses imaginary values of the time 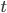instead of real values. Thus, in some sense the proposal, if true, unifies the description of (1) and (2). However, the proposal is far from inevitable, since there is no particularly good reason (*) to think that this special state is the only allowed state of a closed universe in a theory of quantum gravity. There are lots of others, and if God wanted to create the universe in one of those other states, so far as I can see nothing in that choice would be inconsistent with the dynamical Laws of Nature in (2).
(Hawking has a paragraph in his book asserting that the proposal leaves no room for a Creator, but I'll put my comments on that into a later post!)
In the context of a gravitational theory, imaginary time means that instead of thinking about metrics whose signature is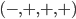 
, as normal for special or general relativity, we think about "Euclidean" (or "Riemannian") signature metrics whose signature is 
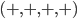. So we have a 4 dimensional curved space (no longer spacetime).
The assumption is that time has an imaginary "beginning", in the sense that it is finite when extended into the imaginary time direction. However, because there is no notion of "past" or "future" when the signature of spacetime, it's arbitrary which point you call the "beginning". What's more, unlike the case of the Big Bang singularity in real time, there's nothing which blows up to infinity or becomes unsmooth at any of the points.
All possible such metrics are considered, but they are weighted with a probability factor which is calculated using the imaginary time dynamics. However, there are some rather hand-waving arguments that the most probable Euclidean spacetime looks like a uniform spherical geometry. The spherical geometry is approximately classical, but there are also quantum fluctuations around it. When you convert it back to real time, a sphere looks like de Sitter space: hence the Hartle-Hawking state predicts that the universe should look have an initial condition that looks roughly like de Sitter space, plus some quantum fluctuations.
I say handwaving, because first of all nobody really knows how to do quantum gravity. The Hartle-Hawking approach involves writing down what's called a functional integral over the space of all possible metrics for the imaginary-time goemetry. There are an infinite-dimensional space of these metrics, and in this case nobody knows how to make sense of it. Even if we did know how to make sense of it, nobody has actually proven that there isn't a classical geometry that isn't even more probable than the sphere. Worst of all, it appears that for some of the directions in this infinite dimensional space, the classical geometries are a minimum of the probability density rather than a maximum! This gives rise to instabilities, which if interpreted naively give you a "probability" distribution which is unnormalizable, meaning that there's no way to get the probabilities to add up to 1.
So Hartle and Hawking do what's called formal calculations, which is when you take a bunch of equations that don't really make sense, manipulate them algebraically as if they did make sense, cross your fingers and hope for the best. In theoretical physics, sometimes this works surprisingly well, and sometimes you fall flat on your face.
Unfortunately, it appears that the predictions of the Hartle-Hawking state, interpreted in this way, are also wrong when you use the laws of physics in the real universe! The trouble is that there are two periods of time when the universe looks approximately like a tiny de Sitter space, (a) in the very early universe during inflation, and (b) at very late times, when the acceleration of the universe makes it look like a very big de Sitter space. Unfortunately, the Hartle-Hawking state seems to predict that the odds the universe should begin in a big de Sitter space is about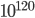 
times greater than the odds that it begins in the little one. That's a shame because if it began in the little one, you would plausibly get a history of the universe which looks roughly like our own. Whereas the big one is rather boring: since it has maximum generalized entropy, nothing interesting happens (except for thermal fluctuations). St. Don Page has a nice article explaining this problem, and suggesting some possible solutions which even he believes are implausible.
Alex Vilenkin has suggested a different "tunnelling" proposal, in which the universe quantum fluctuates out of "nothing" in real time rather than imaginary time. This proposal doesn't actually explain how to get rid of the initial singularity, and requires at least as much handwaving as the Hartle-Hawking proposal, but it has the advantage that it favors a small de Sitter space over a big one. From the perspective of agreeing with observation, this proposal seems better. And it has an actual beginning in real time, something which (despite all the press to the contrary) isn't true for Hartle-Hawking.
(*) There is however at least one bad reason to think this, based on a naive interpretation of the putative "Holographic Principle" of quantum gravity, in which the information in the universe is stored on the boundary. A closed universe has no boundary, and therefore one might think it has no information, meaning that it has only one allowed state! (The argument here is similar to the one saying the energy is zero.) At one time I took this idea seriously, but I now believe that such a strong version of the Holographic Principle has to be wrong. There are lots of other contexts where this "naive" version of the Holographic Principle gets the wrong answer for the information content of regions, and actual calculations of the information content of de Sitter-like spacetimes give a nonzero answer. So I'm pretty sure this isn't actually true.
Hi Dr. Wall,
From what I've read elsewhere ,the Hartle hawking model does involve the beginning of the universe, but has the origin of the universe without a singular beginning point (as it does in other models).
Also ,Dr. Craig would say the imaginary time is just a computational device and in real time (in the actual world) , it would imply a beginning to the universe.
For example see this section on quantum cosmology in the paper here. Deltete and Guy have an interesting paper on how to interpret imaginary time models as well.
You say that "the Hartle-Hawking model doesn't actually have a beginning!" Perhaps you mean that the Hartle-Hawking model doesn't actually have a beginning point or initial singularity? Is the four-dimensional "rounded off" state not the beginning? Indeed, Hawking and Mlodinow themselves use the term "beginning" when describing the no-boundary condition as similar to the South Pole:
"Suppose the beginning of the universe was like the South Pole of the earth, with degrees of latitude playing the role of time. As one moves north, the circles of constant latitude, representing the size of the universe, would expand. The universe would start as a point at the South Pole, but the South Pole is much like any other point. ... In this view, the universe appeared spontaneously, starting off in every possible way" (Stephen Hawking and Leonard Mlodinow, The Grand Design [London: Bantam Books, 2010], 172-174).
Here Hawking and Mlodinow's description implies that such a "no-boundary" universe has a start or beginning (perhaps by tunnelling into existence). This is how John Barrow interprets the no-boundary model:
"This type of quantum universe has not always existed; it comes into being just as the classical cosmologies could, but it does not start at a Big Bang where physical quantities are infinite and where further initial conditions need to be specified." (John D. Barrow, New Theories of Everything: The Quest for Ultimate Explanation, 2nd ed. [Oxford: Oxford University Press, 2007], 91).
Furthermore, although Hartle and Hawking convert time into space for the early universe, some sort of time would still exist because the universe is described as constantly changing and evolving into a larger and larger universe. But such a pre-Big Bang quantum gravity region cannot be eternal - can it? - because such a state is unstable and so quantum fluctuations will cause it to expand or contract from eternity. So I am not sure if a beginning is absent in the Hartle-Hawking model.
Dear LaplaceDemon and James,
Yes, you can find lots of other people saying that the Hartle-Hawking state has a beginning. That's why I put that statement in bold: to clarify a misconception propagated by many other scientists about this subject. The Hawking and Mlodinow quote is talking about what happens if you go off in the imaginary time direction. Not what happens if you go in the real time direction! The universe still exists at arbitrarily large negative values of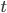
(with high probability), it just doesn't exist for arbitrarily large imaginary values of 
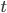. (Here I'm being sloppy since I haven't said what my definition of the 
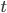coordinate is, but I hope it gives a rough idea. The correct statement would refer to "compact" and "noncompact" geometries.) There could potentially still be singularities in some regions of real space, it's just that things cap off smoothly in the imaginary time direction.
I think part of the confusion here is that people sometimes talk as if imaginary time were an earlier phase in the history of the universe. So they seem to be telling this just-so story: first time was imaginary, and then it became real at a later phase in history (by means of some unknown change-over process which is never discussed). That is NOT the right way to think about it.
Instead you should think of time as being 2 dimensional. It is now complex rather than real. There is a real axis and an imaginary axis. Imaginary time does not come "before" real time, instead they are at 90 degrees to each other. There is no magical point in time on the real axis for which the HH tells you that real time takes over. Rather, the HH state defines a consistent history of the entire evolution of the universe through real time. You can take any path through the complex plane that you like, none of them is better than the others.
HH is just as much a prescription of the "current" state of the universe as it is a prescription of the "early" state of the universe. There is no distinction, because in a gravitational theory like GR different times are really just different ways of representing the same state. That's what the Wheeler-DeWitt equation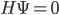
tells us. HH give us a prescription for constructing a particular state obeying the Wheeler-DeWiit equation: that state in turn gives us the entire history of the universe.
Most physicists regard the use of imaginary time purely as a "computational device" as Craig says, so that imaginary time isn't, well, real, and the only thing that really exists is real time. If we accept that point of view, then the HH state is simply one particular state which happens to be (probably) eternal with respect to real time.
On the other hand, if it turned out that it was a Law of Nature (with capital letters) that the universe is in the Hartle-Hawking state, and if the only convenient way to express this Law is using the device of imaginary time, then maybe that would be evidence that imaginary time should be regarded as ontologically real, and not just a calculational device.
I doubt that this reply has cleared everything up: the fact that I had to go on at such length indicates it probably won't do so. But feel free to ask follow-up questions. I wouldn't want to create more misconceptions in the process of dispelling others.
Aron,
You say that "The Hawking and Mlodinow quote is talking about what happens if you go off in the imaginary time direction. Not what happens if you go in the real time direction!" That is exactly the point. Hawking's description of the universe in Euclidean time (or imaginary time) implies that the universe has a beginning at the "South Pole".
But, similarly, as I understand the no-boundary model, real time is finite (and not eternal). It seems, then, irrelevant whether or not we think of time as two-dimensional, since both time dimensions are finite and have a beginning. Perhaps this is why Hartle and Hawking claim that "one can interpret the functional integral over all compact four-geometries bounded by a given three-geometry as giving the amplitude for that three-geometry to arise from a zero three-geometry, i.e., a single point. In other words, the ground state is the amplitude for the Universe to appear from nothing" (Hartle and Hawking, "Wave function of the Universe," Physical Review D 28, no. 12 [1983], 2961).
So, unless the so-called B-theory of time is true, I'm not sure how the universe can be eternal if time is not eternal.
You also claim that if imaginary time is not real (doesn't really exist) "then the HH state is simply one particular state which happens to be (probably) eternal with respect to real time." But how, exactly, does that follow? If imaginary time is simply imaginary and does not reflect reality, then the HH no-boundary proposal is imaginary and does not reflect reality. We can thus only describe the universe literally in terms of real time. And Hawking has made clear that in real time, the universe has a beginning and an end at singularities.
Anyway, the Hartle-Hawking model is a fascinating idea. It would be great if you could write up a post where you give your own criticism of the model.
James,
When you say, "as I understand", do you mean that you gathered this from the quotes of other scientists, more famous than me, who have popularized this model? Well, they were lying to you, and I'm telling you the truth! (OK, they weren't really lying, but rather oversimplifying. I'm sure their motives were as pure as the driven snow, but the end result in their readers' minds is the same.)
Would it help if I said that Jim Hartle, who goes to UCSB, is a personal friend of mine, and that I've seen him give seminars about the HH proposal in which it was quite clear that he believes the states predicted are eternal with respect to real time, and have a "bounce"?
To be fair, the details of the HH predictions depend on the precise laws of physics, and also make assumptions about how to solve the mathematical equations which might (for the various reasons I mentioned in the post) be wrong. So it's always possible that the actual predictions of the HH proposal will turn out to be different from what people expect. I'm not claiming infallibility here, but what I am claiming is a knowledge, via professional expertise and social networking (not to mention working through the physics myself) that it is generally expected that the HH proposal gives a state somewhat like de Sitter spacetime. And it is a fact that de Sitter (in real time, not imaginary time) is eternal and has a bounce in it.
Perhaps you are thinking of the following statement in Hawking's Brief History:
But this statement cannot mean what it appears to at first sight, because earlier in the same chapter Hawking indicates that we don't know whether or not the whole universe will end in a Big Cruch singularity. He must just mean that HH is consistent with the existence of singularities (including those in black holes), not that they necessarily exist in HH with high probability.
Hawking's statement which is so close to being true that I can see why he said it even though it is misleading. The second sentence indicates the context of his statement: it is a contrastive one. He is comparing real time to imaginary time, in which there are no singularities at all, and then indicating that his proposal does not remove singularities from the real spacetime (if they happen to exist in the spacetime produced, is the unspoken condition).
Hmm, I thought I did just write a post (the one you are replying to) in which I indicated some severe problems facing the proposal. To my mind there's nothing left to say about that, except that the HH proposal is a beautiful idea, so that it's a shame that it doesn't seem to work (as normally implemented).
Aron,
Yes. More precisely, I am using their descriptions of this model, especially from Hawkings, to conceptually visualise such a universe as best I can. Perhaps it is too easy to misinterpret these descriptions, or perhaps many of these descriptions are misleading (which will be disappointing). By the way, I'm not sure what fame has to do with it.
No, not really. I guess it is incumbent on me to try to fully understand the mathematics behind the model - this will help!
It is unfortunate that some quotes are misleading.
Fair enough. I misunderstood your post to be a brief reflection on the model (perhaps because of your statement: "Hawking has a paragraph in his book asserting that the proposal leaves no room for a Creator, but I'll put my comments on that into a later post!", a post which I am looking forward to).
I love Vilenkin's book and having that to fall back on, a lot of what you've said I think I actually get (esp. About smaller and larger de sitter space!). Although he definitely gives the impression that he believes his model has a beginning. I'm definitely going to recommend this blog to people. Thanks!
Aron and James,
Correct me if I'm wrong, but, it seems to me that the disagreement between the two of you on the eternality of the HH model lies in the theories of time to which one chooses to subscribe: Aron has stated that he is a B-Theorist; I am assuming that you, James, like myself are also an A-Theorist. So when Aron says,
I take it that Hartle believes this because he subscribes to a B-theory of time in which the entire 4-dimensional spatiotemporal block just exists tenselessly. Thus, it can be said that this block just exists eternally.
However, having a beginning does not necessitate having a beginning point. Time begins to exist just in case for any finite temporal interval, there are only a finite number of equal temporal intervals earlier than it. That condition is fulfilled for the HH model.
Jack,
My point (and Hartle's) wasn't based on A-theory or B-theory. (Most physicists probably aren't even aware of that controversy.) He was talking about models which contract and then have a bounce and then expand again. (If we define "eternal" so that all spacetimes are eternal, that would be a very boring use of the word; there would be no point in saying it except when arguing with an A-theorist.)
No, that condition is not fulfilled for the HH model. Viewed with respect to real time, it goes back to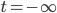
(with high probability). That's what I'm saying.
Aron,
When you say,
are you saying that real time in the HH is sempiternal?
Yes.
Well, it's hard to argue about this with a guy who knows Hartle personally; if he says it, I can't see how is not true. And if so, then you are completely right about this misunderstanding being widespread; tons of the literature that I've read interprets the HH model as being finite in its duration.
I found the slides for Jim's talk about bouncing universes here.
[Update: The audio file is also available now.]
No, that condition is not fulfilled for the HH model. Viewed with respect to real time, it goes back to t=−∞ (with high probability). That's what I'm saying.
This is very interesting. Can you give a source that confirms this explicitly? I have tried to look for this myself, but I'm afraid the information might be buried beneath too much simplification and omission.
It looks like this paper has some discussion of the point:
J. Hartle, T. Hertog, "Arrows of Time in the Bouncing Universes of the No-boundary Quantum State". (see also Ref. [13-16])
It looks like Hawking and collaborators originally considered the probability predictions for a class of nonbouncing cosmologies, and it was later suggested that the bounces are dominant. That may account for some of the confusion.
Another reference is here (see text just below Eq. 10)
A. Vilenkin, "The quantum cosmology debate".
When people say that Hartle-Hawking predicts an inflating de Sitter universe, that almost gets you there since the complete de Sitter spacetime has a bounce. To be fair, there's some uncertainty in how to interpret and calculate results in the HH proposal, so tomorrow somebody might come along with an argument that HH predicts some other type of cosmology. But in any case, the basic conceptual point would still be true: that finiteness in imaginary time is not the same concept as finiteness in real time.
HI dear Aron. some comments .first of all to say that wick rotation is just a computational tool is not a prior correct . It is absolutely likely that imaginary time exists and even be more real that real time at very high energies and curvatures ( planck scale / also this point of view depends on someone view about nature of mathematical structures and objects , if someone like me advocate a pythagorean or platonism view about mathematics so imaginary time or transforming of time direction to spatial direction is not just a trick but something that happens in reality / also often it is said that universe in this model emerges from nothing ! it is not correct , indeed HH proposal tries to give a proper answer to Leibniz famous question why is there anything at all ? HH proposal proves that this question if has a meaningful answer at all , it is doubtless an acausal,a-temporal and a-spatial explanation . and the most primitive era of HH proposal is not nothing rather actually a real something but a peculiar one : a timeless , causation-less ,static. it should be emphasized also to say that HH proposal has no notion of beginning or has notion of a beginning is wrong. both of this words are temporal and so inappropriate in this proposal, it is more better to say emerging of a Lorentzian spacetime from a 4D Euclidean space is a phase transition that we can pose some initial conditions on it exactly at transition point , namely point of silence/ see article asymptotic silence in quantum gravity theories by Jakub Mielczarek ) . Indeed I don't see the term real or imaginary very helpful and it leads to some confusions even among experts . When Hawking says real time replaces with imaginary time ,Hawking means any notion of time simply doesn't exist , instead the notion of time ( real time ) is just exactly a 4 dimension or direction of space . in other word concept of spacetime looses its meaning altogether and we now encounter with just a quantum version of 4D Euclidean space ( Euclidean space is absolutely timeless,causation-less,spaceless ,devoids of any notion of evolution,change ,dynamics and process and utterly static / in 4D Euclidean space there is just 4 spatial directions and so points don't stand in any priority or posteriority relations to each other ( that is very definition of causality in any form ) . Hartle-Hawking no-boundary proposal is truly a very radical and fundamental proposal in all of history and if it would be proved in future , it will have very profound and striking implications for both physical and philosophical (metaphysical ) cruxes . Also recently HH proposal has gotten very strong supports from loop quantum cosmology , string theory ,causal dynamical triangulation and even Horava-Lifshitz Gravity theories . last words : HH proposal simply tries to say many of our fundamental and necessary notions no longer applicable to universe ( at least at the most fundamental ontological level ) . for example as I mentioned above words such as causality ,time ,evolution ,dynamics ,change , motion are totally meaningless concepts at so-called planck scale .
ALL THE BESTS ,
KAVEH
It is absolutely likely that imaginary time exists and even be more real that real time at very high energies and curvatures
And what reasons are there to think that expanding the real numbers into the complex numbers not only does not go too far, but also far enough? Why not go further and replace the complex numbers with the Wiener algebra? It seems just as arbitrary to me.
So is what you say of the Hartle-Hawking model (it being eternal) true of Linde and Vilenkin's?
Vilenkin's model has a beginning of time, yes. (Assuming it is well defined at all). His model assumes that the laws of physics allow the universe to begin in real time, and is defined using a path integral over all such spacetimes. If you look at the wavefunction which he draws for his model in Fig. 1 of his quantum cosmology debate article which I linked to above, you'll see that his wavefunction has only an outgoing expanding piece (his arrow pointing right), with no contracting phase.
In the case of Linde, it's harder to judge since his model is afflicted with terrible instabilities, even worse than Hartle-Hawking, and it's not really clear that there is a well-defined answer at all. But in the simplified model considered by Vilenkin where only the overall size (the "scale factor") of the universe is allowed to vary, it is well-defined, and it seems to me that it predicts a universe which might or might not have a beginning (some significant probability for each).
Whereas in the case of the Hartle-Hawking model, the probability that it has a beginning is extremely tiny (approximately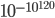
). Assuming that real beginnings are allowed at all, which is a critical assumption of Vilenkin's model but not of the other two models.
Mr. Wall
I find your comments and subtle attempts at de-bunking somewhat disingenuous. Any sensible model we, as creatures within this particular space/time, can create for the beginning of the Universe comes of course to a beginning. And "sensible" here is a key word. There is no doubt that, from our perspective, and based on our senses, that the Universe is about 14 billion (of our) years old. Thus, from our perspective, as creatures and inhabitants of the Universe, clearly it had a beginning, in "our" time, as observed from our perspective. Arguing about which model is better, and which ones "fail" or are weaker, in your view, only serves to obscure the work that has gone into those models and conjectures, and is a misuse of all those arguments to inappropriately argue for an even less convincing "outside" (god-like) "model" for an origin. Hawking plainly states that since it is impossible, from our perspective, to know anything about conditions "before" the origin, due to the singularity, discussing such a moment in time is more than difficult and it is likely that any meaningful explanation of an origin must therefore be somewhat creative. The point he makes is that the calculations work just fine with so-called "imaginary" numbers.
"Imaginary numbers" are no less real than other types of "numbers" and they are quite functional. If those numbers work in the equations, and they do, then his proposal works well enough. The question here is fallibility. Hawking's test in that regard, so far, or at least as I understand it, is that the equations work well enough, and that approach may be all we can do, for now. It is an enormously positive step to get out from under some "god" based origin for the universe. Any falling back to such a god based origin is a return to ignorance and the Middle Ages, or worse.
Mr. Stone,
I find your comments and subtle attempts at de-bunking to be somewhat confused.
Yes, any sensible model we can construct will say that the universe as we know it began about 14 billion years ago. But some of us physicists are interested in the question of what happened before that. Because we are curious, and (quite apart from any religious or anti-religious motivations we may also have) we want to know what really happened! The Hartle-Hawking model purports to be a physical model of what happened at the beginning, and therefore it is fair game for scientific critique. I personally think that the Hartle-Hawking model is a very beautiful idea, but it's difficult to get around the idea that it seems to make wrong predictions, and that certain aspects are mathematically ill-defined (as I said in my post).
The idea that "Arguing about which model is better...or are weaker...only serves to obscure the work that has gone into those models and conjectures" seems to me to be a complete misunderstanding of what scientists do. The main "work" that cosmologists do on models and conjectures, after they make them up in the first place, is to argue about which ones are better...that's how Science progresses! The best compliment you can give to a cosmologist is to take their idea seriously enough to try to refute it.
You don't need to convince me (or any other physicist) that complex numbers play an important role in physics. But that does not necessarily imply that a beginning in "imaginary time" is the same thing as a beginning in "real time". Imaginary time comes up elsewhere in quantum physics, and there it is usually regarded as a trick for defining a ground state or a thermal state, or for calculating tunnelling amplitudes, not as an assertion about how time really works. But if the HH proposal were correct, that might well be a good reason to reconsider whether we ought to take imaginary time more seriously than that...
In any case, you can't forget that I'm writing this blog post for a popular audience. Many people are quite surprised to hear that the Hartle-Hawking state goes back infinitely in "real time" (see the comment thread above) so it seems worthwhile to point this out to people. Yet I happened to mention God in my post, and therefore you accuse me of explaining the science disingenuously, as if I didn't care about getting it right.
You say, "it is an enormously positive step to get out from under some "god" based origin for the universe." In other words, you've decided in advance which direction counts as "positive" and are now looking for evidence which supports that particular conclusion.
You do realize that "People in the Middle Ages believed X, therefore X is false" is a logical fallacy, right?
Richard,
To be disingenuous is to be insincere, by pretending to know less about something than we actually do. So essentially what you're saying is that Aron's comments are an appeal to ignorance (Argumentum ad Ignorantiam). By that definition science is as well. You don't seem to know how science actually works.
When we argue about which models are better and which weaker it isn't to "obscure the work that has gone into those models and conjectures..." It's to separate fact from BS. I hate to be the one to have to break it to you, but hard work alone does not guarantee that one's beliefs or models are actually based in facts... and for that matter, neither does condescendingly redefining ignorance as anything "god based" without regard for said facts. And speaking of facts, now would be a good time for a few...
For starters, it is not true that from our perspective, nothing can be known about conditions before the origin "due to the singularity"--we cannot know about it because there was no "before." That is the point Hawking was making, and it has nothing whatsoever to do with singularities. The universe may or may not have a singularity in its past, and even if it does past-temporal world-lines may not all end at it (the Hartle-Hawking model allows for singularities as well but allows for them to be avoided as a past-temporal boundary). There are hundreds (if not thousands) of mathematically consistent models for the origin and evolution of the universe. Some involve singularities, some don't. Some are past eternal, some aren't. I will grant you that the overwhelming majority of observationally supported models do involve a beginning and the burden of proof is on those who say it didn't (a fact that makes most atheists squirm, special pleading about god-like models being "less convincing" notwithstanding). But those models are as diverse as the cosmologists who dreamed them up... and they cannot all be true regardless of whether "the equations work well enough" or not. You see... this is why we actually test them against observational data and get rid the ones that don't fit the data.
As for the Hartle-Hawking model working "well enough," well guess what my friend... it doesn't! It "works" only in the sense of providing a mathematically workable solution to the Wheeler-Dewitt equation--itself a semi-classical approximation rather than a real quantum gravity theory. The Wick rotation involved (whence comes the "imaginary" time) leads to eigenstates with well-defined space-times without which it wouldn't be possible to generate convergent path integral formulations of the wave function of the universe. But the wave function that actually results from it yields a universe that originates not in a big bang, but as an astronomically large de-Sitter space that looks nothing like the one we actually live in!
Unfortunately, facts don't care what strikes you or I as "less convincing." They don't care about our opinions of what belongs in the Middle Ages either. They tend to be stubborn that way. Which makes your use of the word "sensible" all the more telling. Einstein once defined "common sense" as the repository of prejudice incurred by the average person before their 18th birthday. It seems he was right. ;-)
You know, whatever else might be said about the beliefs of the Middle Ages, at least people in those days based their worldviews on their direct experience of the real world. It wasn't until 20th Century atheism came along that we encounter folks who actually think that pompous opinion, equivocation of terms, and pretty math alone trump real world facts.
Hi Aron,
Enjoyed and appreciate your explanation of the HH proposal. I've a question:
Do you think that the proposal might be interpreted as making the claim that that the universe has a limit but no boundary (or a limit that is not a boundary)? I'm thinking especially of the South Pole geometric analogy, where the South Pole is a limit that can be approached (and used for orientation), but not a boundary that can be transgressed.
Cheers.
Niel,
If we take the imaginary time thing seriously, the analogy to the South Pole is a fairly good one. Mathematically, the statement is that the origin of the universe would be described using a 4 dimensional geometry in which all 4 directions are like "space" and none of them are like "time"; see here for more details about what I mean by that.
Pingback: God loves the odd number – pi2e trillion digits of pi
Pingback: D’après Aurélien Barrau, Univers multiples. La gravitation quantique chapitre 9) | Thomassonjeanmicl's Blog
Pingback: O Discreto Charme do ‘Modelo Cíclico’ | Questões Cosmológicas
Hallo Aron,
I have a little unclarity. Paul Davies wrote in one of his books that in a bouncing chain of universes, each new universe increases (due to the bouncing) its average entropy: therefore an infinite chain of bouncing universes is not possible: one cannot escape the problem of beginning: we still need to postulate a state of very low entropy at the beginning of this chain. Is this not also a problem for Hawking-Hartle model? How do they avoid it?
Wish you all the best!
There is also here an interview with Villenkin from 2012: http://now.tufts.edu/articles/beginning-was-beginning . How does Villenkin view (that the beginning of the universe (or multiverse) is inescapable) fits with Hawking-Hartle view that, in real time, their model implies infinity in both directions?
valentin,
The Hartle-Hawking state does not have an infinite sequence of bounces. Instead, it seems to have a single bounce; the universe expands forever to the future of the bounce, and prior to the bounce it is contracting. (This corresponds to a geometry called the "de Sitter" solution.) As for entropy, in de Sitter the generalized entropy is actually maximal at all times---which is of course bad from the perspective of getting a cosmology like our own!
As for the BGV theorem, it only applies to universes which are expanding (at least on average) for all time. Hence it does not apply directly to a bouncing cosmology, except to say that the expanding phase of the universe must have had a beginning (which it did, at the bounce, since prior to the bounce the universe was contracting).
Thanks, Aron!
In any case, even with this explanation I have some unclarities. I am not a specialist in physics; I have studied philosophy (with a PhD in Thomas Kuhn's epistemology). At the present time I write a book about some arguments for the existence of God (especially in Alvin Plantinga's philosophy); for this reason it would be a great help for me to understand the problem as good as possible. For example, it is intuitively very unclear to me how can an universe infinitely contract (as the idea of an eternal contraction before the bounce would suggest). Has this infinite contraction 'started' from an infinitely - in volume - universe? Is such an infinite volume conceivable? Otherwise, any contraction starting from a finite volume seems to me to suggest a beginning. Or maybe is it rather this infinitely in past 'starting point' of the contraction a finite volume, but somehow asymptotic never reaching a certain limit, like a hyperbola (or a similar geometrical figure)? This would be a first problem. Another one would be: if there is a single bounce, and before it was an infinite time, it seems to me that he have here the question: how it is possible that an unique and non-repeatable event could happen in an infinite duration; to me, in an infinite time a bounce should be repeatable - in fact it should be infinitely repeatable (because in an infinite time, if something could happen, it would surely happen: any why only once?). Origenes had also (in antiquity) another problem related to this situation: how to conceive an event - for example God's creation - in an infinite time: why in this case it happened not 5 millions years later, or 33 billions year earlier (as it actually did)...To conceive an unique event in an eternal time is very hard; therefore he believed in a cyclical universe (Augustine solved later the problem elegantly, by suggesting that God created not just the universe, but also the time together with it).
Valentin,
Good questions! Here are a few thoughts that I hope will be helpful...
First, it's worth noting that these are philosophical rather than scientific questions. Whether actual infinities are possible (as opposed to mathematical ones) is a hotly debated topic among philosophers (and one that's probably beyond the scope of this discussion). Physicists don't generally concern themselves with such matters. For them, the task at hand is to model nature in ways that tell us something about its inner workings. To that end, the only building blocks required are a conceptual paradigm of some sort, reliable observational data that can be quantified parametrically, and a set of differential equations and boundary conditions that describe those observations well enough to make predictions. That's what Hartle and Hawking did here--they started with a quantum mechanical paradigm for the universe and came up with a model that's mathematically viable based on what we know. Beyond that, the fact that it's past/future infinite doesn't really tell us whether the universe itself is. Now it is true that at first blush an actual past/future infinite universe is a reasonable conclusion to draw from such a model, assuming of course that it actually works. But for a variety of reasons (having to do with topology, and also beyond the scope of this discussion) that isn't necessarily the case.
Second, as Aron noted, Hartle and Hawking had to use a mathematical trick called a Wick rotation to get their solution. For lack of a better word, it was a mathematical "kludge" that allowed them to solve a set of differential equations that would otherwise have been divergent and unsolvable. This approach is standard fare in relativistic quantum field theories, which begin with Hamiltonian equations similar to the Wheeler-DeWitt equation (except that they aren't global--for the whole universe). But in these cases it's treated as "scaffolding" needed for workable answers. Once that work has been done, the scaffolding is removed and the solutions restored to temporally real states. Here we're seeking a spacio-temporally global wave function for the universe, so Hartle and Hawking decided to leave the scaffolding in and ponder whether it has actual physical significance. Well, maybe it does... and maybe it doesn't! [For what it's worth, Hawking himself has admitted that it's probably nothing more than a neat mathematical trick.] In any event, IMHO the whole question is moot because, as Aron pointed out, the Hartle-Hawking model doesn't work... it leads to a universe that bears little resemblance to the one we actually find ourselves in! It's in enough trouble already, and questions of real vs. mathematical infinities will only bounce the rubble.
Third, the Hartle-Hawking model is often touted as a quantum gravity model of the universe, but (and this cannot be emphasized enough) it is not! We do not have anything like a viable theory of quantum gravity yet. What Hartle and Hawking actually did was find a solution to the Wheeler-DeWitt equation, which is a semi-classical boundary constraint that we think any viable quantum gravity theory will have to converge to asymptotically below the Planck energy. Whether the universe actually does so or not remains to be seen, and there's some debate as to whether the Wheeler-DeWitt equation is even a consequence of the right path to such a theory. These days most physicists see quantum mechanics as more "fundamental" to bedrock reality than general relativity, so the usual approach to so-called "theories of everything" is to look for ways to "quantize" gravity. But some folks (most notably Roger Penrose) have suggested that the equivalence principle of GR should be treated as more fundamental than the current quantum mechanical framework. If so, the right approach may instead be to "gravitationalize" quantum mechanics. That might sound like hair-splitting equivocation, but the two are paradimatically different and lead to radically different formalisms.
Whichever path one pursues, when the true quantum grativational nature of the universe is revealed to us it's not at all clear that there will be a place for either the Wheeler-DeWitt equation, or whatever mathematical tricks we feel compelled to fall back on today. Neither God, nor His creation are under any constraint to adhere to our needs and expectations for either. :-)
[As always Aron, feel free to fix any errors or omissions here!]
PS - One clarification I could've made better... A past/future infinite universe is a consequence of undoing the Wick rotation in the usual QFT manner. Leaving it in and treating "imaginary" time as more fundamental than real time is what leads to the "no boundary" solution, in which we have a universe that's future, but not past infinite.
Aron,
I have recently read (Rüdiger Vaas: Stephen Hawking korrigiert sein Modell von Urknall), that one of the implications of the Hartle-Hawkins model from 2007-2008 is a reversal (at the bounce) of the arrow of time (in a termodinamical sense): the 'former' universe (which contracted 'before' the bounce), had a different direction of time compared with our (expanding) universe. Moreover, Hawkings saw this idea (at least in the middle of 2007, before completion of Hawkings-Hartle model, as 'a mathematical artefact' ). Are these statements true? And - especially - is the idea convincing? It seems to me to lead in the direction of the critics you raised on this post: that in de Sitter space 'the generalized entropy is actually maximal at all times'.
(In fact, it seems that with the idea of the reversal of arrow of time Hawking struggled for a long time: he wrote an article in 1985 'Arrow of time in Cosmology' in which - against the large consensus of other fellow scientists - he argued for a changing of the arrow of time (when our universe contracts); after a while, he changed in this respect his mind: at the conference 'The beggining of time' (1996) he affirmed that he has dropped this idea. Now it seems that - with the 2008 Hawking-Hartle model - he (grudgingly) returns to it again...
Scott,
many thanks for the clarification!
I would like to add to the discussion an observation: an important point of the debate was whether, according to Hawking, once we return from the imaginary time to the real time, the universe needs to have a beginning (and inevitably we return to a singularity in real time) or if not, on the contrary, once we return to real time we have rather a bounce and an universe which infinitely contracts until the bounce (after which our actual universe starts expanding).
To me, this debate could be solved if one takes into consideration the observation that indeed in his initial no-boundary model (from 1982-1983) Hawkings affirmed that once we return in real time, the singularity is inevitable. In this sense I offer a quotation from Hawking's conference 'The Beginning of Time' (from 1996):
'If space and imaginary time are indeed like the surface of the Earth, there wouldn't be any singularities in the imaginary time direction, at which the laws of physics would break down. And there wouldn't be any boundaries, to the imaginary time space-time, just as there aren't any boundaries to the surface of the Earth. This absence of boundaries means that the laws of physics would determine the state of the universe uniquely, in imaginary time. But if one knows the state of the universe in imaginary time, one can calculate the state of the universe in real time. One would still expect some sort of Big Bang singularity in real time. So real time would still have a beginning. But one wouldn't have to appeal to something outside the universe, to determine how the universe began.'
However, in 2007-2008, Hawking (and Hartle) modify the initial model: the idea of a no-boundary model, of an instanton, remains; but now the modell also takes into consideration the ideas of inflation and dark energy. As a result, the consequence of the model is rather a bounce than a singularity. One has indeed before the bounce an universe that infinitely contracts (see Hartle-Hawking-Hertog article 'The Classical Universes of the No-Boundary Quantum State' from 2008) - an eventually where the arrow of time is reversed.
So, in a sense, both sides of the debate are right...I am open for any correction if I am wrong...
"at which the laws of physics would break down."
They don't actually break down. It is only that the "laws of physics" are our guesses that hold good in certain regimes, say of temperature or density. When these limits are crossed, the "laws of physics" naturally give nonsensical answers and need to be replaced with a better guess.
This is what singularity means--an extrapolation made using a guess that gives nonsensical answer. All it means is that a better guess needs to be made. A mathematical singularity has no connection with "creation of the universe". This point can not be emphasized strongly enough.
Physics is not competent to pronounce on creation of the universe. Physics requires a running universe even to start. All physics does, is to correlate one configuration of particles or fields at time T1 with another configuration at time T2 It makes no sense if there aren't particles at T2.
This dictum of CS Lewis is most edifying:
The sciences bring to the facts the philosophy they claim to derive from them.
From Pilgrim's Regress
valentin,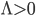
, which leads with high probability to de Sitter solution, which is singularity free, but with smaller probabilities for other things...
You are right that Hawking seems to have changed his positions several times. But in the original Hartle-Hawking paper, they consider a positive cosmological constant
I think the arrow of time reversing at a bounce, is a lot more plausible than the arrow reversing if the universe recollapses (which it currently looks like it won't). But if the entropy is maximal at all times, then there isn't an arrow of time at all! (So any model which predicts that is wrong.)
Scott,
Thanks for your physics remarks to valentin, at a time when I was having greater difficulty typing. I really appreciate your backup support here!
Mostly what you say is correct (or at least, a valid point of view summarizing our current state of ignorance!), but one small correction is that the Wick rotation of de Sitter space would be a (4-dimensional) sphere*, which is actually finite in all directions---there is no distinction between past and future until you rotate back to Lorentzian signature.
*or for purposes of the no-boundary proposal, one hemisphere, ending at the equator. (The no-boundary proposal should really be called the "just-one-boundary" proposal, as opposed to a normal path integral where you have both an initial and a final boundary.)
Thanks Aron! Actually, it was the "one-boundary" 4-D hemisphere that I had in mind, as that's the one that seems to be compared most with the usual big bang singularity models (and the one Hawking made a pretty picture of in A Brief History of Time). I could've been clearer about the 4-D part though. :-)
BTW, how are your hands doing? And how's the interview process going?
Aron,
Is "arrow of time" something empirical in physics? Is there ANY "arrow of time" apart from one we are familiar with?
When you talk about "arrow of time reversing at a bounce", do you mean that entropy starts to decrease rather than increase?
Hi Mactoul,
Yes, there is an arrow of time and it is empirical apart from our existence and perception of it. To see why we need to consider where it comes from.
The laws of physics tell us how things evolve in time, but the equations that capture that evolution don't have a preferred time direction. Imagine dropping a wine glass off a 10th story balcony. It's path to the ground will be described by,
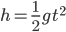
Where h is the glass's height at time t, and g is the gravitational constant. If you plot this function on an h-t graph (t being the abscissa) it will form a parabola. Now the thing is, that graph can be read from right to left as meaningfully as it can be from left to right, and (more to the point here) it is symmetrical about the h axis--the equation works just as well if we substitute -t for t. The same is true for the equations that would describe the wine glass shattering into 1000 pieces and scattering on the ground around the impact site before coming to rest. As far as the laws of physics are concerned, there's no reason why a shattered wine glass couldn't suddenly reassemble itself and leap off the ground into your hand on the 10 floor. So why is it that we never observe such things?The reason of course, is that there are a gazillion more ways to drop a wine glass and shatter it than the reverse. The same is true of light, sound, and other things reaching our senses and registering in our brains rather than the reverse, so this also generalizes to our experience as well. Thus the increasing disorder defined by entropy and the Second Law of Thermodynamics are what gives the universe its arrow of time. As long as the unfolding of some events are more likely than others in one time direction, there will be a valid distinction between past and future whether observers like us are present or not.
There's one caveat to this... Entropy is generally defined as a measure of disorder arising from the transfer of heat in a thermodynamic sense. But there's more to it than that. Apart from a handful of exotic exceptions (e.g. - inflation), the field equations of GR only allow gravity to be attractive, and the equations are non-linear as well (at the risk of stretching things a bit, in one sense you could say that gravity itself gravitates). This also results in a preferred historical direction of events. As time unfolds we only observe the universe's physical matter being drawn together. Everything else held constant, some day it'll all end up in one gigantic black hole. We do not observe the reverse. This is why Hawking was ultimately was able to show that there's a direct analogy between entropy and the area of a black hole's event horizon, thus proving a thermodynamic connection between the two. This allows us to define a black hole's Beckenstein Hawking entropy. Thus, entropy is gravitational as well as molecular.
Imagine a flat universe devoid of matter (or alternately, one filled with a uniform bath of radiation at one temperature, and a cosmological constant just large enough to statically offset the 4-D curvature resulting from its energy). Past and future would have no meaning in such a universe because nothing would ever change there. Every event on its space-time manifold looks just like every other. Time would be distinct, but only in the sense of having a different metric signature (-1 as opposed to 1, or in the case of wick-rotated imaginary time -i). No clock would unambiguously discriminate between past and future, any more than a ruler would unambiguously separate one direction as forward rather than backward. But as long as a universe contains mass-energy, and some sequences of events are more likely in one time direction than another, there will be an arrow of time whether that universe contains observers like us or not.
As always, if I'm mistaken (and in this case I may well be) I trust he'll correct me. But regarding the arrow of time reversing at a bounce, I believe what Aron is referring to is a suggestion that's been made by a few folks that if the universe has (or "had") a recollapsing phase, entropy might've decreased during it (at least the gravitational part)--sort of like running the movie backwards--giving a different arrow of time. If so, a bounce might have reset that to the direction of increasing entropy. But if entropy actually did run backwards in such a phase and we were present, it's not clear to me that our perceptions of past vs. future would be any different than they are now. And if a bounce (or bounces) were to occur at a singularity, it seems to me that it would be more meaningful to speak of a bunch of universes emerging from one singularity with their own time arrows, rather than one bouncing repeatedly into some indefinite future. In any event all of that is moot because as Aron said, it doesn't look like the universe is headed toward a recollapse anyway.
Best. :-)
PS - One qualification to my last. As I've written it, my equation defines "height" negatively, as pointing downward from where the wine glass was dropped. While that made my point clearer, it's not a very useful definition of "height." :-) In the more usual sense of the word, the equation would technically be
![h = h_{0}\left [ 1 - \frac{1}{2}gt^{2} \right ]](http://www.wall.org/~aron/blog/wp-content/plugins/latex/cache/tex_cc14dd488783e0a498cdeccb372af6fe.gif)
WhereScott,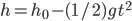
.
You put the parenthesis in the wrong place. Should be
Ugh... obviously! [Smacks his head with a mixing spoon...] I was in too big a hurry to correct the other. Thanks Aron! :-)
Scott, you say the discussion of the bounce is moot because it does not look like the universe will recollpase. I dont see why this make this moot at all. You could easily have an hourglass universe. i.e just a one time bounce with infinite expansion and infinite contraction on either side of the bounce point. This would be perfectly consistent with the universe not re contracting in the future so those observations our completely irrelevant to whether there was a bounce in our past. Its like saying I can't have come from Australia because Im not going to Australia. that just doesn't make any sense.
What we can say is that many people working in many different approaches to quantum gravity ( both string and loops ) have suggested that singularities are replaced with bounces. In other words singularities are simply forbidden in the fundamental theory. We believe that In GR there is a singularity in our past , that gives you then, if these ideas are correct, at least one bounce. If there is a singularity in our future that could give more than one bounce.
I agree that the leading candidate for dark energy is a cosmological constant. If thats correct then the universe wont re collapse. But how confident are we that we really understand dark energy ? I think not very confident at all, in which case, we should not rule out the possibility that dark energy might something that changes over time so we can't rule a re collapse. Even though I agree its not the favoured scenario. So even that statement that the universe isn't going to recollaps is not really on a strong enough footing to make this discussion moot, even if it were relevant for a past bounce, which for the reasons explained above it is not.
As for the arrow of time at the bounce. I've heard several suggestions. One is that the arrow time reverses at the bounce. This means if there are observers on the other side of the bounce they see time going forward but from our perspective we think they are in our past and vice versa. This is known as the Janus universe. In this scenario the entropy goes down if you are looking at getting closer to the bounce point.
At a recent conference on time at the Permitter Institute Abhay Ashtekar suggested something which seems to be quite different, like an entropy rest at the bounce, 23 minutes and 11 seconds into this video:
http://pirsa.org/displayFlash.php?id=16060112
So the entropy is going up in the contracting phase as you get close to the bounce point, but doesn't go through into the expanding phase.
A further alternative is that the entropy goes up from pre bounce to post bounce but just our local entropy is small I think this is what happens in ekpyoritc models, which are different as they are cyclic rather than a one time bounce.
Thats my understanding anyway.
As far as I can see no one knows which of these scenarios are right.
Hallo Aron,
I have another unclarity regarding our subject: you wrote on your post that:
“Alex Vilenkin has suggested a different "tunnelling" proposal, in which the universe quantum fluctuates out of "nothing" in real time rather than imaginary time. This proposal…has an actual beginning in real time…”
However, W.L. Craig and James Sinclair argued that Vilenkin’s model does not work, because the initial state of the universe explanatorily prior to tunneling, postulated by him, cannot be equated with nothingness: a truly quantum tunneling from nothing implies that the function (which describes the quantum tunneling) should have only one term, the posterior one - and this is not the case for Vilenkin's model. I offer you in what follows the quotation:
“Vilenkin invites us to envision a small, closed, spherical universe filled with a so-called false vacuum and containing some ordinary matter. If the radius of such a universe is small, classical physics predicts that it will collapse to a point; but quantum physics permits it to “tunnel” into a state of inflationary expansion. If we allow the radius to shrink all the way to zero, there still remains some positive probability of the universe’s tunneling to inflation…Vilenkin equates the initial state of the universe explanatorily prior to tunneling with nothingness. But postulating such an equivalence is grossly misleading…For Vilenkin…quantum tunneling is at every point a function from something to something ...For quantum tunneling to be truly from nothing, the function would have to have only one term, the posterior term. Another way of seeing the point is to reflect on the fact that to have no radius (as is the case with nothingness) is not to have a radius, whose measure is zero. Thus, there is no basis for the claim that quantum physics proves that things can begin to exist without a cause, much less that universe could have sprung into being uncaused from literally nothing.” (In Blackwell Companion to Natural Theology, p. 183).
My question would be if the aforementioned assessment is right - at least from the perspective of an A theory of time. Could not someone say that, for example, that “no radius” (the nothingness of Craig and Sinclair) CAN in fact be legitimately be equated with an universe whose radius’ measure is zero? Conversely, can we say indeed, without any incoherence – at least from the perspective of an A theory of time -, that according to Vilenkin, it is possible that an universe may appear from nothing, through quantum tunneling (I understand by nothing the absence of space and time – and also of God; I guess, even if we would eventually allow that with this nothingness might also co-exist numbers, mathematics, logic, Platonic ideas, eventually the abstract laws of science, all these would make no difference to the story, because they are abstract objects unable to make any difference to our story).
"One clarification I could've made better... A past/future infinite universe is a consequence of undoing the Wick rotation in the usual QFT manner. Leaving it in and treating "imaginary" time as more fundamental than real time is what leads to the "no boundary" solution, in which we have a universe that's future, but not past infinite."
I think this was the answer I went here to find. I'm a post-doc physicist myself, but cosmology is not my forte. I had the question emerge in an informal debate regarding imaginary time: what would an observer actually see?
First, a question the quoted answer raised, though: I was under the impression that there still emerges a singularity in real time. Would this give a singularity in an 'hourglass' configuration? Someone suggested that but I felt like the answer given was not entirely clear.
So, in that case, suppose some being (to borrow from Einstein 'what sort of being is immaterial for our purposes') is sitting in the universe at what, from our point of view, is the point when the universe looked like a small deSitter space (or space-time if you prefer). Suppose this extends backwards to what we would call the 'beginning' of the universe. Call this point O. Now, let us consider that observer's world-line. Let us construct that world-line by supposing that it extends to 'us' sitting here on Earth in 2017. Call this point 'U' (for 'us'). Now, consider the observer at some 'earlier' point in the world-line, defined in this case by moving along his world-line such that the motion is opposite the direction that would lead toward U. Call this point E. Make it such that intervals OE and OU are equal in magnitude (that is, their ds^2 values are equal). I go through all this trouble because I know enough about cosmology to know that you have to be careful defining things like 'direction' in cosmological contexts. Now, let us assume OU is time-like in the 'normal' Minkowski space-time sense, without consideration for imaginary time.
So suppose that observer at some 'earlier' point on his world-line then progresses along that world-line towards the point. Under the HH model, what will this observer observe? The interval OE would also be time-like under the traditional definitions, but under imaginary time it's not clear if the phrase 'timelike' has any meaning.
Let us make some more specific examples. Suppose we give this observer a 'light clock', where time is measured by how long it takes light to bounce between 2 mirrors. Einstein used these to illustrate SR, though I suspect Aron knows that. Would it continue to dutifully tick away from his point of view? It seems unreasonable to think it wouldn't, unless the observers world-line has a terminus, but HH claims it wouldn't if imaginary time is 'real', to my understanding.
Next, suppose the observer at point E sends out a light pulse. Would it be possible for him to observe this pulse at point U? At point O? What if the pulse is emitted at point U? What if we add a second, parallel observer: could a world-line be constructed such that the pulse at E is visible from two separate points on the new world-line? If it is, what would this observer say about the light-clock?
Sorry for all these questions: it's not a criticism of you. I've never understood what Hawking and Hartle were trying to say about 'imaginary time', even after getting a PhD in physics myself (though the differing speciality doesn't help), and this way of formulating the question occurred to me when I encountered this article. Hope you can at least elucidate the questions, if not the answers. XP
Personally, because of these questions, I don't see 'imaginary time' as working quite the way HH seems to imply, but as I'm not sure I understand what HH is saying, I can't be sure...
And related to this, another problem: Sinclair and Craig suggest that the contemporary quantum cosmologists are averse to the Copenhagen interpretation of quantum physics, because it implies an ultramundane observer to collapse the wave function of the universe (I would add that probably they would probably also reject the idea of the measure instrument collapsing the wave function at the beginning). John Polkinghorne stated in his Short Introduction to Quantum Theory that the majority of the physicists today are inclined toward a neo-Copenhagen interpretation of quantum physics. Is it this also the case with the contemporary quantum cosmologists?
valentin,
The question of whether a 0-radius universe is the same as no spacetime, depends on the subtle question of whether quantum gravity allows topology change (most people in the field think yes in at least some contexts), and if so whether the nucleation of a universe from no space at all is an example of an allowed transition. This really depends on the details of the quantum gravity theory. Vilenkin is really only saying, if it is possible, then here is what would happen next.
While Vilenkin isn't religous, I don't think he's trying to make any sort of metaphysical statement about the non-existence of God, nor is he trying to make a statement about absolute nothingness a la Krauss. That's not really what respectable physics models do. Think of it more like: "Here's an interesting candidate for the initial state of the universe? I wonder what predictions it makes?"
I would say that most physicists don't think about issues of interpretation very much!
When somebody identfies as "Copenhagen", that often just means that they think a lot of the founders of QM had some good things to say, but they haven't thought about it in much detail. "Copenhagen" is really just mismash of a bunch of things Bohr, Heiseberg, Born etc. said, and calling it an interpretation is a little bit like calling "Chinese Traditional" a religion.
I think people who work on quantum cosmology are a bit more likely to be interested in questions of interpretation, and are probably more likely to lean towards things like the many worlds interpretation.
By the way, it is really really hard to make sense of quantum cosmology with an A-theory of time. Like, the fundamental equation of the theory, the Wheeler-de Witt equation, pretty much states explicitly that the wavefunction includes a contribution from all possible times. And like GR, there is no natural notion of simultaneity.
A Henderson,
The HH state predicts the universe is in a de Sitter spacetime, which is a Lorentzian solution with no beginning of time or singularity. As long as we make all our measurements in Lorentzian spacetime, the universe has no beginning. It's only if we "analytically continue" in the imaginary time direction that spacetime looks like a sphere, with 4 space dimensions (and also no singularity).
Also, it doesn't really make sense to talk about observers and lightrays on a Euclidean sphere.
It's important not to get confused by those diagrams where you see half a sphere joined to half a de Sitter solution. Are you familiar with complex analysis and analytic continuation from your physics education? If so, what's really going on here is analogous to an arbitrary choice of "contour", where you suddenly choose to start going in the imaginary direction instead of the real one. I'd say that physics is what happens along the real time axis, and imaginary time is just a mathematical fiction which is sometimes useful for defining "special" states.
Thanks for responding. Ok, so it's an analytic continuation. I was missing that piece I think.
I've encountered analytic continuation, but I never did much with it. I think we touched on it in Quantum II (grad level), but I didn't go on to Field Theory and I don't recall my other classes mentioning it. I took intro to complex analysis at one point, but it was was back in undergrad, and I've not used it much sense.
Apparently I was picturing it wrong, and so phrased the question poorly, but your response suggests an answer, or at least a question. If there is no sense in talking about observers, in what way can it reflect reality? Any solution of general relativity should at least be able to describe light-like geodesics, or in what way is it a solution? If a theory cannot make actual predictions of what would be seen, then it's hard to see how it COULD reflect reality.
Your next paragraph, however, answers that question at least from your end: It doesn't reflect reality, it's a mathematical fiction. If it's not possible to situate an observer in the HH model, that suggests that that's an inevitable interpretation.
I don't think I'm familiar with the diagrams you're talking about, though. I've usually seen that solution just as a sphere, and I guess assumed it was analogous to the "closed" solution, where you can view the sphere as either 2 spatial dimensions and one time-like one.
Anyway, thanks for answering. I'm still not completely clear but my thought that the HH universe couldn't reflect reality has been strengthened.
Thanks a lot for your answer, Aron! I was very interested to know what Vilenkin would answer to Craig's objection.Regarding the way in which quantum cosmologist interpret quantum physics, if their only acceptable interpretation to it is the 'many worlds' one, then, as I have read, they might have here a problem: among the other interpretations, the 'many worlds one' seems to be, according to some physicists, the most fishy. Polkinghorne, for example, wrote about it: 'this is a proposal of astonishing ontological prodigality. Poor William of Occam must be turning in his grave at the thought of such a multiplication of entities.'
Aron
I would have also, if possible, another question: I do not understand very clear the distinction between an A-theory of time and a B-theory of time. Could you recommend me some bibliography in this respect?
valentin: You know, I had a debate with someone about this awhile back. Unfortunately we didn't have time for me to figure out the disconnect and explain it to him, but it amounted to this: I said that a quantum multiverse has to explain why we only perceive one path. He seemed to reject the entire premise that that was true, which I never figured out, as unless he is some sort of higher life form, he also only experiences a single reality.
@A Henderson, as a matter of fact, tomorrow I will be posting the second installment in my series on interpretations of quantum mechanics here, and among other things, it will be tackling that very question. :-)
valentin,
I didn't mean to imply that all quantum cosmologists accept MWI (and I certainly do not). But, perhaps as a direct result of working in their field, they tend to be more sympathetic to interpretations that allow them to talk about the wave function of the entire universe, as if it were a closed system.
As for A vs. B theories of time, I've discussed them before in the first 3 posts of this series.
Many thanks Aron!
Sorry to bring up an old horse but I just noticed this old quote from Hawking
"Only if we could picture the universe in terms of imaginary time would there be no singularities.... When one goes back to the real time in which we live, however, there will still appear to be singularities"
Hawking, Brief History of Time, pp. 138-139.
Im wondering how you square that with your comment that in real time there is bounce not a singularity? Has Hawking got it wrong, has the understanding of the model changed? or...?
howie,
is positive (which makes it easier to have a bounce rather than a beginning of time).
Yes, he (probably) had it wrong. (Stephen Hawking is a great man, but he is not the Pope of Science.) I think Hawking was overconfident in his book about the interpretation of the HH state, and since then it has been discovered that the cosmological constant
However, in the original paper they primarily examine the case of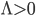
, and say it represents de Sitter spacetime, and it is uncontroversially true that dS has a bounce.
Pingback: No Boundary Proposed or not? – The nth Root
Thank you so much for taking the time to reply. But I guess like in all good science, one answer opens up more questions. I thought De Sitter space was just empty space filler only with a cosmological constant. Have I got this wrong? As i understand it the cosmological constant causes space to expand at an accelerated rate. So I don't see how De Sitter Space leads to a bounce. I thought in order to get a bounce you needed some exotic matter or some quantum geometry effect like in loop quantum gravity. Can you explain ? I am very confused.
Hello. It's me again.
1- Can i understand vilenkin's model as a "classical" universe that emerges from a prior existing quantum state?
If so, how do we know that this "state" from which the universe tunneled from began?
Howie,
> I thought De Sitter space was just empty space filler only with a cosmological constant.
That is correct.
>As i understand it the cosmological constant causes space to expand at an accelerated rate. So I don't see how De Sitter Space leads to a bounce.
In one coordinate presentation of de Sitter space, space at one time is a sphere of radius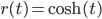
, where 
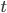is proportional to the proper time as seen by a family of observers who remain stationary on the sphere. Since ![\cosh(t) = [e^{t} + e^{-t}]/2](http://www.wall.org/~aron/blog/wp-content/plugins/latex/cache/tex_7be3a814dc7fdf94f17f241ecdbb1af1.gif)
is a function that goes down and then up again, in this coordinate system it looks like there is a contracting phase, followed by a single bounce to an expanding phase. The second derivative of this function, i.e. its acceleration, is always positive. (Perhaps you thought I was saying that there is a bounce after the expanding phase; if so you were right to be confused because there isn't anything like that.) It should be pointed out however, that dS is a maximally symmetric spacetime, so every point is related by a symmetry to every other point. Thus it is a coordinate-dependent question whether a given point is in the expanding or contracting phase. But if you add matter to dS (so that it is no longer exact dS) this symmetry goes away.
(There is another coordinate presentation of dS where space at one time is a Euclidean plane, which is perpetually exponentially expanding like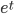
, but this version is not complete, it turns out to be only half of the complete dS as described in the previous paragraph.)
There exist various singularity theorems which rule out cosmologies which replace the Big Bang singularity with a Big Bounce. However, for various reasons described in the post I linked to, none of them apply to dS (or nearly dS) cosmology! In particular, dS is spatially finite, and a positive cosmological constant violates the Strong Energy Condition.
Pingback: A Speaker for Stephen Hawking (1942-2018) – The American Catholic
Hi, Dr. Wall. You stated that “Alex Vilenkin has suggested a different "tunnelling" proposal, in which the universe quantum fluctuates out of "nothing" in real time rather than imaginary time. This proposal…has an actual beginning…”
The problem here is that it seems atheists are correct in pointing out that no quantum model allows the universe to come from absolute nothingness. The Vilenkin proposal, for instance, use the WheelerDeWitt (WDW) version of quantum gravity and in the WDW formalism, one represents the quantum state of the universe as Ψ on superspace. How can one claim that something arises from nothing, when this nothing is at minimum, minisuperspace?
Furthermore, there are many deep problems with the WDW view here as Singh Kohli explained in his article "Comments on: A Universe from Nothing" https://arxiv.org/pdf/1405.6091.pdf
What do you think about this paper? I await your response.
Sheers.