A reader who wishes to be anonymous writes in with the following question:
I heard your paper referenced in the Carroll vs Craig debate, attempted to read it, then looked you up and found your blog (which I really like!!). I’m fascinated by the origin of the universe and think it is a great argument for a creator. I have a question I’m hoping you can help me with, or better yet, do a blog post on so I have something to reference!
Frequently when I debate an atheist online, they will bring up the argument that the net energy of the universe is zero and so the First Law of Thermodynamics was not violated at the origin of the universe since energy was still conserved. As they explain it, the positive energy of matter is countered by the negative energy of gravity. Our universe formed from a freak quantum fluctuation and is the ultimate free lunch. I understand this at a very simple level, but what I do not understand is how a zero-energy universe matches what we observe. If matter only makes up ~5% of the universe, 30% if you include dark matter, then how does the universe have a net energy balance of zero if 70% of it is dark energy pushing the universe apart through repulsive gravity? It seems the expansion of the universe indicates a net positive energy. Could you please give a simple layperson explanation for why folks like Hawking, Krauss, Guth, etc claim the universe has a net energy of zero? It feels like there is a slight-of-hand going on and dark energy is being excluded, but I don’t know enough or have any sources to point to that say otherwise.
Dear Reader, thanks for your question. I notice there's an interesting inversion here from the Carroll-Craig debate. In that debate, St. Craig was trying to argue that the universe had a beginning, and Carroll was trying to outmaneuver him with the "Quantum Eternity Theorem", saying that the universe couldn't have begun unless its total energy is zero. He then opened himself up to the retort that the energy probably is zero.
On the other hand, in your debate, it's the atheist who seems to be championing the position that the energy of the universe is zero. Presumably this is because he wants to say that the universe emerged from a Nothing somewhat like the one Krauss' has in mind (though all this talk of Nothing doing things as if it were Something keeps reminding me of "The Nothing" in The Neverending Story...) and therefore `no room for a Creator' etc. In this case the theist might argue that Energy Conservation makes this impossible (absent a miracle), opening herself up to the retort that the energy probably is zero.
So perhaps if you and Craig were locked in a room together, you might discuss whether a physics-type beginning of the universe is helpful or unhelpful, when arguing for Theism. Alternatively, there could be a Krauss-Carroll debate about whether there's less "room" for a Creator with or without a beginning of time (both of them granting that the idea is absurd either way). One could more or less construct such a debate just from their remarks directed against Theism already linked to on this blog. Carroll could argue that in models like Aguirre-Grattan:
There is no room in such a conception [an eternal universe with the entropy lowest in the middle] for God to have brought the universe into existence at any one moment.
and Krauss could respond that:
It has become clear that not only can our universe naturally arise from nothing, without supernatural shenanigans, but that it probably did.
and Carroll could retort that:
That is not what the universe does even in models where the universe has a beginning, a first moment. Because the verb popping, the verb to pop, has a temporal connotation, is the word I'm looking for. It sounds as if you waited a while, and then, pop, there was the universe. But that's exactly wrong. The correct statement is that there are models that are complete and consistent in which there is a first moment of time. That is not the same as to say there was some process by which the universe popped into being.
Apologies to Krauss and Carroll for wrenching their remarks totally out of context, but I believe I have not done any violence to their actual views. If you'd rather see what the real Carroll actually said about Krauss' conception, you can find that on his blog here.
But that wasn't your question. Setting aside which team benefits more from it, what does physics say about whether the energy is zero?
As I said when discussing the "Quantum Eternity Theorem", there are lots of different concepts of energy in General Relativity, and even the experts sometimes find the relationships between them tricky to think about. It's no wonder laypeople get confused when the "experts" make definitive sounding pronouncements about the subject. If the energy at every point in the universe is positive, how could it possibly be true that the total adds to zero?
Well, the ``simple layperson'' explanation is that in cosmology, there's contributions to the energy both from 1) matter (baryons, dark matter, dark energy, etc.) and 2) from spacetime, stored in the gravitational fields. There's a notion of energy density where you only count category #1, and then the energy density is positive. But this notion isn't very useful for discussing things like energy conservation, since it isn't conserved in situations where space is changing with time (e.g. expanding). There's another notion where we count both #1 and #2, and then it turns out that the contribution from #2 is negative and (in a finite sized "closed" universe) the total is zero.
That's the best I can do without launching into technicalities. But I can't resist trying to say more about the real story, even if what follows may not really count as a simple layperson explanation.
Perhaps it would be easiest to explain if we start with a theory that's simpler than GR. GR is in many ways quite similar to an easier theory of physics, namely Maxwell's equations. Like the gravitational field, the electromagnetic field is sourced by a particular type of matter. Gravitational fields are produced by the flow of energy and momentum through a spacetime, while electric and magnetic fields are produced by the flow of charge.
Let's just think focus on one of the Maxwell equations right now, the Gauss Law. This is a special type of Law of Physics called a constraint. That means, instead of telling you how things change with time, it places restrictions on what is allowed to be the case at a single moment of time.
The Gauss Law is written in equations like this:
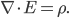
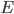is the electric field vector at any given point, and 
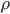is the rate at which charge is flowing through time at a given point. Which is a really fancy way of saying, the charge density. 
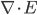means 
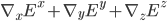, where 
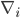means taking the derivative with respect to the 
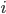-th spatial coordinate.
But maybe you hate equations: if so you are in good company. When I was at St. John's College we read a funny letter in which St. Faraday wrote to St. Maxwell, saying that he loved his work, but why did he have to write it using math? St. Faraday, you see, lived in the time where you could still be a respectable scientist and explain everything using words. Very carefully chosen words, expressing precise quantitative relationships.
Anyway, Faraday figured out this brilliant way to visualize the Gauss Law, which we still use as a crutch today. Instead of thinking of 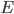as a vector, you can think of it as a density of electric field lines passing through a point. The direction of the vector says which direction the lines are going in, and the magnitude says how many there are. I'm sure you've seen electric and magnetic field lines before, but if not, here are some pretty pictures on Google.
The Gauss Law says that electric field lines can only begin or end on charges. The number of electric field lines coming out of (into) a charge, is proportional to the positive (negative) charge of the particle. (We say "number" to make it easy to visualize, but in fact the field lines form a continuum.)
This means that if you have a region of space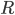 
, you can do a census of the total charge in that region, simply by measuring the total amount of electric field lines coming into or out of that region. One can write this as an equation too:
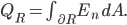
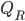is the total charge inside the region , 
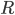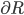is fancy-schmancy notation for the boundary of , 
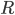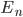is the number of electric field lines poking out per unit area, and 
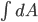tells you to integrate that over the whole area to get the total number of electric field lines poking out. (Faraday would have said, why work so hard to invent these silly symbols when you could just say "count the number of electric field lines poking out"?) We physicists call an integral like this a boundary term, because—go figure—it's the integral over a boundary of a region.
We are now in a position to appreciate the following interesting truth. Suppose the universe is closed. (That means, finite in size but without any boundary. For example, space at one time could be shaped like a giant hypersphere; as we all know a sphere is finite in size but has no end. Or like one of those video games where if you go off the edge of the screen on one side, you "wrap around" and appear on the other side, so that there isn't really an edge there.) In a closed universe, the total electric charge is always EXACTLY ZERO.
If you're Faraday, that's because each electric field line has to either circle around in loops, or else begin on a positive charge and end on a negative charge. So everything has to balance out. If you're Maxwell, it's because if you take the region 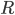to be the whole universe, then 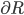is the empty set, and so the Gauss Law just says 
.
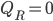This doesn't necessarily have to be true if space is infinitely big. You could just have a single electric charge sitting in infinite empty space, and this would be OK because the field lines beginning at the charge would go out to infinity, so they don't need another endpoint.
Now what about GR? It turns out that things work in a very similar way, only using energy instead of charge. If the universe were a single star or a galaxy sitting in an otherwise empty infinite space, then the gravitational ``field lines'' coming out of the mass extend out to infinity. This allows the total "ADM" energy of the spacetime to be nonzero. In fact, there is a Positive Energy Theorem in GR which says that, for reasonable types of matter, this energy is always positive for any state besides the vacuum (which has 0 energy).
On the other hand, if the universe is closed, then the total energy is zero because there's no boundary for gravitational field lines to go off to. But how can this be, when the cosmologists tell us that the universe consists of about 5% ordinary matter, about 25% dark matter and 70% dark energy, and each of these components of energy is positive?
(I hate the term ``dark energy'', by the way, since it makes people think it's related to dark matter. The two are nothing alike. Dark matter is just some other kind of stuff, which clumps into structures. The so-called dark energy is most likely just a cosmological constant, i.e. a constant positive energy density throughout all of space.)
To answer this, I need to remind you of how Einstein's equation of GR works. The Einstein equation says how energy and momentum lead to spacetime curvature. It can be written like this
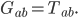
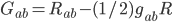is called the Einstein tensor; basically it's a 4x4 symmetric matrix which encodes certain properties of the curvature of spacetime. On the other hand, 
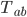is the stress-energy tensor of matter. This is also a 4x4 symmetric matrix, which encodes the rate at which momentum in the 
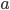-direction is flowing in the 
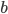-direction. (The 
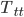component, where both indices are chosen to be time, is just the energy density, since energy is momentum in the time direction.)
A key point here is that 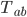only counts the energy and momentum in matter. It does not count the energy and momentum stored in the gravitational field (although by convention, these days most people include the cosmological constant or ``dark energy'' in 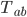). When the cosmologists tell you about the "energy budget" of the universe, they are only really talking about 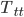. They are ignoring the contribution from the gravitational field, which also contributes to the total energy of the universe. It turns out that in a closed universe, the gravitational part (due to 
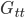) counts negatively and this exactly cancels the matter contribution.
Defining the total energy of the universe is, as I said, quite tricky, since in the Hamiltonian formalism energy is related to time, and you have to make an arbitrary decision about what counts as the ``time'' direction. You have to decide this separately for every single point, so there's actually a lot of arbitrariness here. Once you've picked a time coordinate, if you want to evaluate the total energy on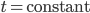 
slice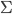 
, the total energy 
ends up being given by something like the following integral over the volume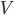 
of space:
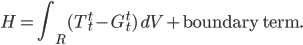
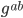.) The boundary term is an integral 
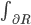of something I'm not bothering to write down.
Now the t-t component of the Einstein equation, a.k.a. the Hamiltonian constraint, tells us that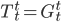 
. So the whole thing boils down to a boundary term, and in a closed universe that has to be zero. Thus, the ambiguity about time doesn't matter in the end, since "0" is conserved no matter what.
Epic. You should make youtube videos. Carroll, Craig, David Deutsch, Massimo Pigliucci, Antonie Suarez, luke Barnes, Michio Kaku, John Templeton foundation and Tom Campbell etc. do it.
I'm loving this series. Great stuff.
So for a closed universe the total energy must sum to zero? It appears you answer is yes because the boundary term has to be zero in a closed universe. Can you explain to us laymen why the boundary term has to be zero in a closed universe?
Perhaps I can provide a basis for a laymen’s example by describing a scenario of taking all the mass of the universe uniformly spread over the surface of a sphere with a very large radius so the mass is all very far apart so the gravity force is essentially zero. So then the gravity energy would be zero. Then let all this mass come to the center by gravity. Since the mass is coming closer together the gravity potential is decreasing, but the gravity is causing the acceleration which increases the kinetic energy by the same amount of decrease in gravity energy. So then when all the mass meets simultaneously at the center the negative gravity energy is equal to the positive kinetic energy summing to a total energy of zero. So the initial big crunch ending point would have a zero total energy. Reverse this scenario you have a big bang starting with zero total energy.
So through this picture I can see how the total energy could be zero, but I do not see why it has to be zero. Aron does the math you explained also describe this scenario? What would be the boundary term in this scenario? Can you describe an open, flat or closed universe using this scenario? This scenario leaves out dark energy. How could dark energy being added to this scenario and the energy still total to zero? The key question is can you explain by this scenario why a closed universe total energy must always sum to zero?
The zero energy seems to come from this definition of zero gravity energy which Ref. 1 says is just a convention. Is it really just a convention to define zero gravity energy when the masses are so far apart so the Gravity force is zero?
Ref. 1: https://en.wikipedia.org/wiki/Gravitational_potential
I realize in my scenario I left out the energy of the mass = m * c^2. Since you are using the math of GR which determined E = m * c^2 then perhaps you can still somehow use this scenario to explain by a picture why a closed universe total energy must always sum to zero.
David, Luke,
Thanks for the compliments.
Personally I find text a much more conducive medium (to the extent that I was unwilling to sit through the Craig-Carroll debate until I found a transcript), so for the time being I'll stick with that.
Dear Steve,
The reason why a boundary term has to vanish in a closed universe is simple, almost a tautology. A boundary term is by definition an integral over the boundary of space. If space is closed, it has no boundary (i.e. the boundary is the empty set) and so the result is zero. It's like adding together a sum of zero terms; the result is always zero.
Now let me make sure I understand your scenario. Spacetime has 4 dimensions, so space has 3. When you say that the matter is uniformly spread out over a very large sphere, you mean a 2 dimensional sphere, yes? So that the matter is not uniform over all 3 dimensions of space, but is confined to a 2 dimensional subspace located an equal distance from a central point.
I want to observe that this is very different from the example of a closed universe I mentioned, in which the matter is uniformly distributed over a hyperspherical geometry. That is, the geometry of the universe would be shaped just like the surface of a sphere sitting in a 4 dimensional space, but this is just an analogy because the extra spatial direction has no actual existence---GR is about the intrinsic geometry of space and time as measured by beings within it; it does not postulate that space is bent within any higher dimensional space...
In your example, space is open, not closed. We know this because the density of matter is very thin, and therefore the corresponding geometry should be very close to flat Euclidean space. But flat Euclidean space has a "boundary" at infinity, so the gravitational field lines can go off to infinity. Hence the total energy does not have to be zero in your example; instead it should be positive.
And it is positive, for the reason you mention: you have to include the mass-energy of the stuff using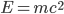
. So the total energy is positive, and of course is conserved as the spherical shell begins to collapse. When it reaches the center it will form a black hole, not a big crunch (time will end only in the center of the black hole, not everywhere). If you want a closed universe with a big crunch, you'd have to have a different distribution of matter, e.g. a uniform matter distribution which would tend to cause space to be curved like a hypersphere.
Your Ref. 1 is discusisng the gravitational potential in the context of Newtonian gravity. In this context it is true that you can add a constant potential everywhere and it doesn't change anything, because the force is the derivaive of the potential. The convention that the potential goes to zero far from any matter is often a good one, but it is still a convention.
In GR there is an analogue of this issue, but it is more subtle. In GR the gravitaitonal potential is basically the rate at which time is flowing at a particular point. However, this quantity is somewhat ambiguous since it depends on your choice of "time" coordinate, and we are free to use whatever coordinate system we like. If you had a clump of matter like you describe, you could choose to use a weird coordinate system where, even far from the matter, time flows at a faster or slower speed than 1 real second per coordinate second. It might be a silly thing to do, but it's not against the rules.
Hi Luke:
I couldn’t agree with you more. What an excellent blog. I have been looking for one like this for a long time. I tell what I like about it: Although we all know St. Aron’s Christian bias, but he does not let it intrude into his physics and, as one with a mathematical background, I like that separation of Church and State.
As for the format I’m old fashioned and I like the written word because good writing demands clarity and coherence I must add honesty, and so I like reading Aron’s pieces and the comments.
I would like Aron to put all of this meaty stuff in a book.
Would you, Aron?
Thank you.
Pingback: A Response to Aron Wall’s Zero Energy Universe Article – Chaining Reality
I have posted a response to Dr. Wall's article on this link:
[link is no longer valid]
[Name Removed],
I appreciate all the kind things you said about me in your response. But I'm afraid I have to be blunt and say that I don't really see much point in debating this issue with Dr. Kohli by proxy. Until you yourself know the math behind the ADM formalism of General Relativity, I don't see how you can be in a position to know that I have "missed the point".
Presumably Dr. Kohli does not deny that the Hamiltonian density (which is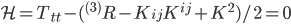
up to a total derivative term) vanishes in a closed universe. This is not really debated among cosmologists. He must just be disputing whether this is in fact a reasonable thing to call "energy". But that is just a question of definitions. As I acknowledged in my main post, there are multiple possible concepts that go by the name of energy. Some of them are well defined in an expanding universe, others are not.
The fact that the Wheeler-de Witt equation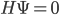
seems to imply the absense of time evolution is a well-known issue in the quantum gravity community, sometimes called the "frozen formalism" or "the problem of time". I (and I think most other physicists working in the field) take this as a sign of the fact that there is uniquely defined "t" coordinate, rather than as a sign that there is no dynamics, or that the WdW equation needs to be modified.
Also, at several points in your response, you seem to be confusing the electric charge with the energy. At certain points in my explanation I was using the former as an analogy to the latter, but these are not the same thing!
Sir , I've heard many people claim that the first law of thermodynamics proves that the energy/matter must always exist in some form or another, since it cannot be created or destroyed. This would mean that energy/matter had no beginning, and will have no end. Is this a valid claim? Or is there something I'm misunderstand about the conservation law?
Dr. Wall,
Thank you for this post. I have been trying to get my mind around the proposition that the universe has a sum total of 0 energy and I think that this post is helping to clarify that. I am one of those people who only understand basic math but are much more adept at abstract representation and I'm still having some trouble seeing the practical aspect of a 0-energy universe. I understand that matter/energy is conserved and that it seems as though that process results in the transition of various "things" from one state to another; heat, mass, etc. Meaning that we do not "add" heat we transform it into/from something else. (perhaps that is wrong)
The problem I have in wrapping my head around this notion is that if the actual energy level of the universe is truly zero where is the expansion/stretching energy coming from? I have heard that there was a precise amount of matter and anti-matter where there was slightly more in quantity than anti-matter. It was a close-to-zero number, but not zero itself.
Perhaps that is the source of my confusion. It seems as though I can make sense of things if the sum total of energy in the universe is *almost* zero, like matter/anti-matter, but I have a hard time making sense of it if it is only-and-exactly zero to explain an expanding universe. From a philosophical perspective it sounds to me like equivocating a true "nothing" and a "vacuum". Is it an "actual" zero or a "close enough to zero that we can say zero?"
A second aspect of this that doesn't make sense (since I'm here writing anyway), is that it seems as though some physicists confuse 0 with NULL, using them interchangeable. Would that be accurate?
Kevin,
Any time an object is in motion (i.e. changing with time) then it has kinetic energy. The expansion of space with time is no exception. However, it turns out that in general relativity, the energy stored in expanding (or contracting) space is negative, not positive. This is a quirky result, but it follows from standard rules for how to calculate the energy in general physics theories.
So in our cosmology, each point in space has a negative energy density due to the expansion of space. However, by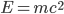
there is also positive energy density due to the mass of matter (ordinary stuff and also dark matter). Finally, there is a positive energy density of ordinary empty space (called the "cosmological constant" or "dark energy"). One of Einstein's equations of general relativity implies that the sum of these positive and negative contributions have to exactly cancel. Hence, the energy density of the universe is zero, and the accounting all works out.
(By the way, it turns out that antimatter has positive energy just like matter does.)
I don't know what you mean by NULL, but there is a very important distinction between a quantity being zero, and a quantity being undefined. In this case it is zero. But that of course does not mean that the universe does not exist, any more than having a bank account with a debit account and a credit card debt where the two sum to 0 dollars would mean that your bank account is "nothing".
It seems to me that if you sum the Gaussian Curvature across Spacetime that the result of an appropriate cross section will yield a value of Zero. Even the ultra large scale of the observable universe reveals vast bubbles of empty Spacetime encapsulated by walls of fibrous matter. The curvature of the voids are negative, the cross sections are zero and the locations of matter are positive(folded Spacetime).
The recent measurements revealing that the known universe has a curvature of zero makes a compelling argument for Infinite Spacetime where the Universe is in a state of Infinite magnitude and eternal duration. This means that the Universe was never, never created on the scale of the totality so there is no event where God created the Universe. When you define God as the creator of the Universe and prove that the Universe was never created, then the only conclusion is the Nonexistence of God is a fact!
Robert,
Your second paragraph doesn't follow from the first at all.
Just because space is infinitely big, doesn't mean time lasted forever. In fact the Penrose singularity theorem specifically applies to universes that are spatially infinite.
Also, measurements can only indicate that the curvature is very close to zero, but never that it is exactly zero. And even if the curvature of space is zero, doesn't mean that space is infinitely big. It could have a nontrivial topology, like a torus.
Finally, there is no reason why a universe of infinite magnitude and eternal duration could not have been created by God. God's power and wisdom are infinite so his mind can embrace as a "totality" even an entity which has infinite spacetime volume. (In fact, St. Georg Cantor has demonstrated how it is logically possible to consider an infinite set as complete, and construct from it even bigger types of infinities.
Theologically speaking, "creation" refers not to a first moment of time, but rather to the fact that all reality is metaphysically dependent on God to exist.
Hello.
I have one doubt (I apologize if it has already explained): if the negative energy of the gravity field of a star is extremely low comparing to the positive energy of the matter it is made up of, then the positive energy of a galaxy must be much higher than its negative energy.
Therefore, why in the universe as a whole both quantities are the same and cancell each other? Who adds the extra negative energy to compensate this?
Polatw,
Your objection presupposes the intuition that it is possible to calculate the total energy of the universe by dividing the universe up into regions and adding up the energy in each region. This is an extremely reasonable intuition, but it turns out to be very problematic in general relativity, since it is not really possible to define the energy in a coordinate independent way in each region. As I said in the previous post in this series:
In the special case where we have an expanding FRW cosmology, we can define the energy density due to matter in a relatively unproblematic way, and this is positive everywhere. But if we try to include the gravitational energy (which is needed to have a valid conservation law) in a region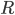
we find out that we need to make a bunch of arbitrary choices and the result ends up being 0 except for a term that depends in a weird way on the boundary of 
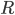(and the choice of some clock ``time'' on this boundary). By weird, I mean you can't just add up all the local energies and get a good answer for the whole universe.
It's a very unsatisfactory situation, but there are two special cases where you get a pretty good answer. The first case is if you imagine that the universe contained only a single galaxy sitting in the middle of empty space, and you try to measure the total mass of the universe by the strength of its gravitational field very far away, as you go out to infinity. In that case, you get that the total energy is always positive---matching your intuition. This is called ADM mass. The second case where things work out simply is if the universe has no spatial boundary at all (e.g. if space is a giant hypersphere). In that case, if you take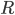
to be the entire universe, there is no boundary and so the total energy is zero.
But if you want to talk about the energy of part of the universe, there ends up being no very satisfactory way to do that. This is a weird consequence of the coordinate invariance of general relativity.