A bunch of people have been asking me about the interpretation of QM. Now, every interpretation of QM predicts (or claims to predict) the same experimental results in any experiment (or at least, any realistically feasible experiment). Otherwise they wouldn't be rival interpretations, they would be rival theories, and we would just do an experiment to see who is right.
So before discussing what QM actually means, it's good to get the ground rules down—the ones that all physicists agree are the right ones to use to predict the results of actual experiments.
Let's suppose we're doing a physics experiment, which I am going to describe in an extremely abstract way, because that's the kind of person I am. A (somewhat idealized) way to describe a certain class of experiments is as follows: We start out by preparing the initial configuration of the apparatus to be in some particular configuration (or "state"), let's call it A. For example, we start with a radioactive atom. We can let the experimental apparatus evolve on its own, isolated from the rest of the world, until it reaches some final configuration. Then we look inside, e.g. 10 minutes later, and check what the current state of the experiment is. Perhaps the atom has now decayed into something else. Let's call this final configuration B.
Several aspects of this description are clearly idealizations. There are always some limitations in our ability to control and/or know the initial condition A; the system is never going to be completely isolated from the rest of the world no matter how hard I try. And in some experimental setups this may be a good thing—that is, we may want to deliberately reach in to measure and/or adjust the system, part way through its "time evolution". (Unlike biologists, we physicists use the word evolution any time anything changes!) And, at the end of the process, we're never going to be able to measure the final outcome with perfect precision either.
But I'm a theorist so I can ignore the messiness of real life, whenever it pleases me to do so.
Now if the laws of physics were deterministic (and if we know what they are, and we know the initial state completely precisely...) then in principle we could simply solve all of the relevant equations and find out what exactly the final state would be. So after 10 minutes, any given A will become some particular B with probability 1.
(In practice, this calculation is often impossible because of phenomena like chaos where (in some systems, not others) the final outcome depends very, very sensitively on the initial conditions. For chaotic systems, you need to know the initial conditions to exponential precision in order to predict the future. This is why we can't predict the weather accurately for more than about a few days out, because the number of digits accuracy you'd need to measure things to is proportional to the number of days!)
But the actual laws of physics are stranger than that. They are not deterministic. I think I've read that some Philosophers of Science claimed that Determinism was an important assumption underlying the possibility of doing Science at all. Well, Determinism is false, and yet we scientists still have jobs. I know, 20-20 hindsight, but it was still a dumb thing to say (if anyone in fact ever said it, which I haven't done the research to confirm...).
So let's try again. Once again, we'll set up our experiment in a particular initial state A. But now, there are several possible final states B, B', B'' etc. Let's suppose we want to calculate the probability for some specific one: B. So the sane, sensible way of doing this, would be to think of all the different ways that A could evolve in time to become B. To actually do calculations, you apply the rules of probability theory:
NORMAL PROBABILITY THEORY:
- For any particular process by which A can evolve to B (a history), we survey all the events which happened in that history, and calculate the probability of each individual event (using our knowledge of the laws of physics, as worked out from experiment or theory) Then we multiply those probabilities to calculate the probability of that particular history.
. - If there is more than one distinct history going from A to B, then we add up the probabilities of each history (since each of them are separate possible ways to get B), to get the total probability of observing B.
. - At the end of the day, the probabilities for all possible final outcomes should add up to 1.
Note that, since probabilities are between 0 and 1, multiplying them makes them smaller, as befits situations where multiple unlikely things need to happen to get from A to B. On the other hand, adding them makes them bigger, as makes sense if there's more than one way for something to happen.
This is the sort of probability theory which would make sense a priori to our rational minds. The kind from which you can prove sensible results like Bayes' theorem. But the universe doesn't really work that way either!
One way to think about QM is that it's like a Behind the Looking Glass version of probability theory, where things almost work like how you expect them to, but not quite. The basic weird idea of quantum mechanics that instead of assigning each path from A to B a probability (which is a real number between 0 and 1) you assign to each path an amplitude (which is a complex number whose absolute value is less than or equal to 1).
A complex number can be thought of as just a vector lying in a two-dimensional plane. In order to specify it, you need to know how long it is (the "absolute value" of the complex number) and what direction it points in (the "phase" of the complex number). Of course, if the absolute value is zero, then the phase is meaningless, since the complex number is just 0.
In QM, the absolute value squared of an amplitude represents the probability for an event to happen. This is called the Born rule, and it is the necessary interface for getting actual predictions about the world out of the theory.
So let's suppose you have two different possible ways to go from A to B. (A classic example is the double slit experiment, where a particle passes through a screen which has two holes in it, and then reaches one of several possible locations on the detector.)
If the two possible histories have the same phase, then they constructively interfere and the probability of B happening is more than you would expect, from adding up the probabilities of the two histories. On the other hand, if the two possible histories have opposite phases, then they destructively interfere, and the final probability is less than you would expect. In fact, if the amplitudes are equal and opposite, then the total probability of getting to B is exactly 0!
(More generally, amplitudes constructively interfere if they are at an acute angle in the complex plane, and destructively interfere if they are at an obtuse angle. For right angles, the Pythagorean Theorem + the Born Rule tells you that you get the naive expected answer from just adding up the probabilities.)
So, to summarize, instead of doing the thing that makes sense, you do this instead:
QUANTUM PROBABILITY THEORY:
- For any particular process by which A can evolve to B (a history), we survey all the events which happened in that history, and calculate the amplitude for each individual event (using our knowledge of the laws of physics, as worked out from experiment or theory.) Then we multiply those amplitudes to calculate the probability of that particular history.
. - If there is more than one history going from A to B, then we add up the amplitudes of each history (since each of them are separate possible ways to get B), to get the total probability of ending up at B.
. - The probability of observing B is given by taking the absolute value squared of the total amplitude. Unlike amplitudes, this is always a real number between 0 and 1. Also, the laws of physics are chosen so that, at the end of the day, the probabilities of all possible final outcomes still add up to 1. (This requirement is called unitarity). QM may be weird, but it's not that weird.
(You may wish to go back and compare this, point by point, with the Not-Batshit-Crazy-Probability-Theory earlier in the post.)
So, if you have a system with N different initial states (and therefore N possible final states), you can specify the time evolution over any given time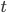 
by writing all of the possible transition amplitudes from each possible initial state A, A', A''... to B, B', B''... in an N x N matrix 
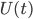, with complex numbers in each slot. If you know about the math of matrices, this matrix is required to be unitary: 
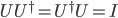. That's what enforces unitarity, the rule that probabilities add to 1 no matter which state you start with.
Now, if you wanted to know which specific states are allowed, or which specific unitary matrix to use, then you need to specify a particular quantum mechanical theory, e.g. a harmonic oscillator, or Quantum Electrodynamics., or the Standard Model. QM is a framework for constructing theories, not a specific theory. Just like Newton's Law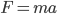 
, or the rules of classical physics, are a general framework; only experiments can tell you which particular forces actually exist in Nature.
In the next post of the series, I'll spell out some of the implications of this framework, and then maybe I'll be in a position to talk about interpretation.
I'm really looking forward to this series, Aron.
Hi-lar-i-ous.
This is very clear--are you going to do Feynman path integrals?
Thanks, Aron
Nice. Is this going to be a whole series of posts on interpretations of QM?
Happy new Year BTW :)
Great stuff Aron! I'm really looking forward to this series too. If I may, I have a few requests for enlightenment too. I'd love to get your take on the following,
1) Many Worlds... Like you I think it's crazy, but a lot of folks claim it's the most "economical" interpretation at least in part because it avoids wave function collapse (although it isn't the only one that does this). The idea seems to be that the mathematical economy of not having to deal with "measurement" trumps the philosophical nightmare of relinquishing unique histories. On the other hand, decoherence doesn't strike me as mathematically economical either. What are your thoughts on this?
2) Consistent Histories, which from what I've seen seems to be the most popular alternative to MW and Copenhagen...?
3) Non-locality (vis 'a vis Bell's Theorem)... especially spacio-temporal non-locality (which to me at least seems potentially relevant to questions of free will vs. B-theory time).
4) Your take on counterfactual definiteness in all this.
Btw, in case you haven't already seen it Wikipedia has a great tabular summary of the alternatives and their features. As always, thanks! :-)
Andrew, Scott,
My main goal (after explaining the physics) was to explain why I don't like MWI. Assessing every single interpretation out there sounds like a lot more work than I'd planned! But obviously I'll have to say something about my own, very tentative beliefs about interpretation.
Bob,
The three rules that I wrote down for Quantum Probability Theory, are very closely related to the Feynman path integral. It's almost the same thing.
The main additional idea is that, if you really consider every possible path that a particle could use to go from point A to point B over a given time, (not just e.g. the straight lines passing through particular slits) then not only is the space of all possible paths continuous, it's even infinite dimensional! So you have to assign an infinitesimal amount of amplitude to each particular path, and then figure out a way to integrate them all over this whole infinite-dimensional space of paths.
This is called functional integration and it's a lot scarier than the normal kind of integration they teach in basic Calculus classes. In fact this is the real reason for all the infinities which tend to pop up all over QFT. Although for the quantum mechanics of a finite set of nonrelativistic particles, it's not so bad.
(Perhaps you know this already from your own physics training, but of course you won't be the only person reading my response.)
Thanks Aron for the spiel on Feynman path integrals. I knew some of that, but not all, the bit about functional integration. My Ph.D. is in chemical physics (E.B. Wilson, Jr.) and my research has been in magnetic resonance, so perhaps I'm not entitled to be a "real" physicist, even though I've published papers in QM.
Thanks Aron. I don't think you would want to address every interpretation either... that would be a chore! But given that Copenhagen and MWI both have major issues, practical and philosophical, it's worth asking what the best alternative to both is among the others. I mentioned Consistent Histories only because last time I checked it seemed to be the one most commonly discussed. No one seems to take Bohm's Hidden Variables approach seriously anymore... not after Bell's Theorem anyway. Never mind all of 'em... is there at least one that you think stands out practically and philosophically as a good alternative to Copenhagen and MWI?
[Maybe none of the available alternatives will turn out to be workable... Personally, if it comes down to Copenhagen or MWI I'll take Copenhagen any day of the week... :-) ]
Aron, like the rest of the comments, I am grateful you will be tackling this question. Eagerly looking forward to it and from all I've read above, it will be good education.
Hi Scott, I am very much fascinated by Louis de Broglie's pilot-wave theory (1927). It's not exactly de Broglie-Bohm (1952), but also hidden variables, right? I've read some interesting fluid dynamics analogous experimental confirmation (at MIT under John Bush) of parts of the interpretation. Bell supported de Broglie's theory as "seems so natural and simple, to resolve the wave-particle dilemma in such a clear and ordinary way, that it is a great mystery that it was so generally ignored" (1986). Well, after all he was the one who pointed out flaws in von Neumann's proof of the probabilistic interpretation. Any further thoughts?
Thanks, I've been waiting for this series Aron since you intimated this back in 2014.
Raschid,
Pilot-wave theory certainly seems intriguing. As a "hidden variable" theory it resolves quantum paradoxes by attributing quantum behavior to underlying deterministic variables that for practical rather than philosophical reasons cannot be observed, but at the price of accepting non-locality in physics. I don't know all that much about it so I can't speak with any authority. But if I understand things correctly, the main reasons it hasn't gained much traction are that it requires "empty waves" that cannot be observed, and it only accounts for a limited number of quantum phenomena compared to more traditional interpretations. Most physicists seem to consider it a fascinating and fruitful area for research, but ultimately ad-hoc and of limited utility compared to more traditional interpretations. The work of Bush, Couder, and others is promising, but the extent to which their macroscopic observations extrapolate to the subatomic realm is unclear. Wired magazine has a pretty decent article on it and how it's viewed by the physics community. To be honest, I don't feel informed enough about it yet to have a strong opinion, but at first blush I'd take it in a heartbeat over MWI even though the latter avoids empty waves. Aron, do you have any thoughts on this that aren't soon to appear in a coming installment?
Ah yes, this is in fact the article I read! Thanks for your thoughts, Scott. Yes, the Couder experiment can only serve as analogy at this point and as you say "the extent to which their macroscopic observations extrapolate to the subatomic realm is unclear". On the other hand here's another recent paper from Nature http://tinyurl.com/jjgzoe7 Hensen et al, Delft University of Technology to which The Economist refers marking "an end to hidden variables", which, anyway it says, "most physicists reckon the idea... flawed". I am always skeptical when the media gets too excited and so I linked the paper itself for your reference. Anyway, I hope to gain better understanding through this series to try to evaluate the interpretations myself even as a layman.
Scott & Raschid,
Well most physicists probably don't think much about Bohmian interpretations at all, but I think among those that do, a big annoyance is that it (a) requires faster than light signalling, and (b) it requires picking a particular basis (e.g. position vs. momentum) in the Hilbert space, which seems kind of arbitrary. (I'm pretty sure the most natural basis to pick in QFT will be different than that in QM, by the way, since in QFT the analogue of "position" is the value of the fields at each point.) On the other hand, at least it has a nice probability interpretation.
Regarding the droplets-on-liquid analogy in that link, I strongly suspect it only works for single particle quantum mechanics, and breaks down when there are interference effects involving 2 or more particles. If there are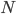
particles in a 
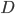-dimensional space, then there are 
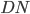position degrees of freedom and so the wavefunction lives in a 
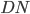-dimensional space. But normal physical waves in a material only live in a 
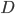-dimensional space. (Normally 
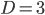in free space QM, but 
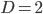for particles moving around on the surface of a liquid.)
I have another comment/question. Are you going to touch on information theory as a foundation for quantum mechanics? I've been doing some reading--Zeilinger, Christopher Timpson's thesis--some of the math is over my head, but my general impression is that while the mathematical framework can be established, the physics is left out. But perhaps I'm unperceptive. In any case it would be a very fine thing if you could bring your intelligence and knowledge to bear on this--it seems to be a hot topic.
This is an absolutely magnificent exposition. Thank you. -Leon