In Time as the Fourth Dimension?, I explained how to calculate the distance (or duration) squared between any two points of spacetime, using a spin-off of the Pythagorean theorem:
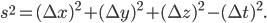
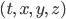 that don't change the formula for
that don't change the formula for 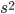 .
.
Well, it turns out that I lied. The formula isn't actually true, except in the special case that there is nothing in the universe. A significant reservation, I know. Instead, what's true is that the geometry of space is a field, meaning that it varies from place to place, depending on where you are! However, if you zoom in really close at any particular point, it looks similar to the formula I told you.
The field that says what geometry is like at any given place and time is called (brace yourself) the gravitational field. In order to describe it, we use something called the metric, which indicates what the geometry of spacetime looks like at any given point. The way this works is, suppose we have two points 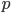 and
and 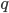 which are very close to each other. Suppose we want to know the distance between these points.
which are very close to each other. Suppose we want to know the distance between these points.
Since the points are really close to each other, we call the distance between them 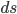 , where the
, where the 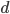 is just a reminder that we're using Calculus to study infinitesimal quantities. If you don't know Calculus, just pretend these are really small numbers. We want to figure out what
is just a reminder that we're using Calculus to study infinitesimal quantities. If you don't know Calculus, just pretend these are really small numbers. We want to figure out what 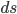 is, if we know the infinitesimal coordinate differences
is, if we know the infinitesimal coordinate differences 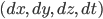 . The way we do this is by generalizing the heck out of the Pythagorean theorem. I'll write it down, and then explain what it means:
. The way we do this is by generalizing the heck out of the Pythagorean theorem. I'll write it down, and then explain what it means:
![(ds)^2 = g_{xx}\,(dx)^2 + g_{yy}\,(dy)^2 + g_{zz}\,(dz)^2 + g_{tt} \,(dt)^2 + \\ 2[ g_{xy}\,dx\,dy + g_{xz}\,dx\,dz + g_{xt}\,dx\,dt + g_{yz}\,dy\,dz + g_{yt}\,dy\,dt + g_{zt}\,dz\,dt].](http://www.wall.org/~aron/blog/wp-content/plugins/latex/cache/tex_db669a03022d92c818e3bbe67f915b2f.gif)
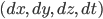 . There are 4 different ways to pick the first
. There are 4 different ways to pick the first 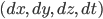 , and 4 different ways to pick the second, which gives
, and 4 different ways to pick the second, which gives 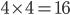 possible combinations in all. However, multiplication is commutative so e.g.
possible combinations in all. However, multiplication is commutative so e.g. 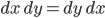 . So I added terms like that together; that's where the factor of 2 came from. Taking that into account, there's 10 terms in all.
. So I added terms like that together; that's where the factor of 2 came from. Taking that into account, there's 10 terms in all.
The funny 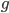 things with subscripts are just functions of spacetime, i.e. they are just numbers that depend on where you are, i.e. they are fields. In the special case where we pick these numbers to be
things with subscripts are just functions of spacetime, i.e. they are just numbers that depend on where you are, i.e. they are fields. In the special case where we pick these numbers to be 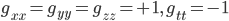 and the rest zero, we get the geometry I told you about, which goes by the aliases "Minkowski space", "flat spacetime", and "Special Relativity". In all other cases we have what is colloquially called "curved spacetime" which is the province of "General Relativity".
and the rest zero, we get the geometry I told you about, which goes by the aliases "Minkowski space", "flat spacetime", and "Special Relativity". In all other cases we have what is colloquially called "curved spacetime" which is the province of "General Relativity".
The formula above looks kind of ugly, but we can prettify it by choosing good notation. We collectively refer to all ten of these gravitational fields as the metric, denoted 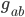 , where subscripts like
, where subscripts like 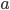 and
and 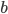 can refer to any of the four coordinate labels. (People often call these labels
can refer to any of the four coordinate labels. (People often call these labels 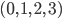 instead of
instead of 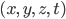 to avoid confusion, since the metric itself says which of the coordinate directions behave more like space, and which behave more like time, and this can vary from place to place!) Then we write the four coordinate differences
to avoid confusion, since the metric itself says which of the coordinate directions behave more like space, and which behave more like time, and this can vary from place to place!) Then we write the four coordinate differences 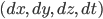 collectively as
collectively as 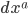 , where the superscript says which of the four it is. Finally, we make up a rule called the Einstein summation convention, that if we ever see the same letter as both a subscript and as a superscript, we add up all of the four possible ways for them to be the same (i.e. both 0, both 1, both 2, or both 3). These are just changes in how we write things, not substantive changes, but they let us rewrite that long ugly equation like this:
, where the superscript says which of the four it is. Finally, we make up a rule called the Einstein summation convention, that if we ever see the same letter as both a subscript and as a superscript, we add up all of the four possible ways for them to be the same (i.e. both 0, both 1, both 2, or both 3). These are just changes in how we write things, not substantive changes, but they let us rewrite that long ugly equation like this:
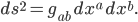
Suppose we want to find the distance (or duration) between two points which are NOT infinitesimally close to each other. In that case, we have to choose a path between the two points, since the amount of distance (or duration) depends on which path you choose, and in a curved spacetime there's not necessarily one "best" path. This shouldn't seem that strange, since even in everyday life we know perfectly well that the distance between San Francisco and L.A. depends on which highway you take, and the distance between Tokyo and New York depends on which way around the globe you fly. (It's totally intuitive for distances, but when the duration depends on the route you take through spacetime, people call it the Twin Paradox and act all shocked!)
So this is the first main idea of General Relativity: the geometry of spacetime is a field which varies from place to place. This field affects matter by determining the paths that things take through space and time, but it also is affected by matter—we call this gravity. The second main idea is that coordinates are an arbitrary choice; I'll tell you about this later. The third main idea is the Einstein equation which says how matter affects the metric. I haven't told you anything about this equation yet, but once I do, you would in principle be able to calculate everything about the gravitational field from that one equation.
There can also be distortions of the spacetime geometry which exist independently of matter. These gravity waves are to gravity what light is to electromagnetism, ripples in the field which travel through empty space, and can be emitted and absorbed. The propagation of these waves is also determined by the Einstein equation. Since gravity comes from massive objects, gravity waves are emitted when extremely large masses oscillate, for example when two neutron stars orbit each other. We know gravity waves are there, but we haven't detected them directly. However, we hope to detect them soon with the LIGO experiment.
UPDATE: I realized that I never said how you would calculate the distance between two points, once you choose a path. The answer is that you chop the path into lots of tiny little line segments, and find the length of each line segment using the metric. Then you add them all up. If you know Calculus, this can be done using an integral.

To lie is to state something that you know to be false as truth. Did you do that?
That was a joke. If you click on the link you'll see what I really meant.
I certainly knew that Special Relativity isn't completely true. But it is an approximate truth, which is helpful for leading people on to greater truth. So I guess you could say I was lying when I said I lied ;-). But of course, jocular falsehoods which one expects the audience to recognize as jokes aren't really lies, since there is no intent to deceive.
Please fix the typo in the expanded main equation above.: (ds)2=gxx(dx)2+gyy(dy)2+gzz(dz)2+gtt(dt)2+2[gxydxdy+gxzdxdz+gxtdxdt+2yzdydz+gytdydt+gztdzdt].
2yzdydzshould be gyzdydz
Sorry I can enter subscripts in this box (or at least I don't know how)
Thanks, David. It should be fixed now.
You can write equations in LaTeX as long as you put them inside of a pair of double dollar signs. You can break it out into its own line by adding a ! after the first double dollar sign.
Dear Aron: Regarding gravitational waves, shouldn't the pulse of neutrinos from Supernova 1987A be regarded as a gravitational wave? Rapid change in the gravitational field releasing a wave of energy at the speed of light. Neutrinos, 99% of the energy of the crushed star, must be the unbound remnants of destroyed nucleons. All the gravitational energy of the star becomes unbound and released at speed c. SN1987A tells us neutrinos travel at c.
I know particle physicists want neutrinos to have a rest-mass because of "flavor-oscillation". That would slow the neutrinos down. That's really shaky theorizing, in the face of SN1987A. Your thoughts?
Dear Roy,
Just because neutrinos are produced at a time when there are rapid changes in the gravitational field, does not mean that they are gravity waves! In the Standard Model + GR, neutrinos are a completely different kind of beast than gravity waves. Neutrinos are spin-1/2 and interact with ordinary matter via the weak force. Gravity waves are spin-2 and don't interact via the weak force (and thus we couldn't possibly detect them with neutrino experiments). They are completely different things.
The neutrinos from SN1987A did indeed travel at the speed of light up to experimental error. But if the mass of the neutrino is sufficiently small, energetic neutrinos would still travel very very close to the speed of light, so we couldn't tell the difference. According to Wikipedia's summary of an article on SN1987A, the experimental results are consistent at 95% with any neutrino mass smaller than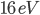 . Whereas, in order to explain flavor oscillatons, you only need masses of about
. Whereas, in order to explain flavor oscillatons, you only need masses of about 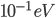 or so. So that's consistent.
or so. So that's consistent.