Interpreting the Quantum World I: Measurement & Non-Locality

In previous posts Aron introduced us to the strange, yet compelling world of quantum mechanics and its radical departures from our everyday experience. We saw that the classical world we grew up with, where matter is composed of solid particles governed by strictly deterministic equations of state and motion, is in fact somewhat “fuzzy.” The atoms, molecules, and subatomic particles in the brightly colored illustrations and stick models of our childhood chemistry sets and schoolbooks are actually probabilistic fields that somehow acquire the properties we find in them when they’re observed. Even a particle’s location is not well-defined until we see it here, and not there. Furthermore, because they are ultimately fields, they behave in ways the little hard “marbles” of classical systems cannot, leading to all sort of paradoxes. Physicists, philosophers, and theologians alike have spent nearly a century trying to understand these paradoxes. In this series of posts, we’re going to explore what they tell us about the universe, and our place in it.

To quickly recap earlier posts, in quantum mechanics (QM) the fundamental building block of matter is a complex-valued wave function 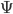$\Psi$ whose squared amplitude is a real-valued number that gives the probability density of observing a particle/s in any given state. 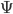$\Psi$ is most commonly given as a function of the locations of its constituent particles, 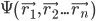$\Psi\left ( \vec{r_{1}}, \vec{r_{2}}... \vec{r_{n}} \right )$, or their momentums, 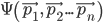$\Psi\left ( \vec{p_{1}}, \vec{p_{2}}... \vec{p_{n}} \right )$ (but not both, which as we will see, is important), but will also include any of the system’s other variables we wish to characterize (e.g. spin states). The range of possible configurations these variables span is known as the system’s Hilbert space. As the system evolves, its wave function wanders through this space exploring its myriad probabilistic possibilities. The time evolution of its journey is derived from its total energy in a manner directly analogous to the Hamiltonian formalism of classical mechanics, resulting in the well-known time-dependent Schrödinger equation. Because 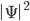$\left | \Psi \right |^{2}$ is a probability density, its integral over all of the system’s degrees of freedom must equal 1. This irreducibly probabilistic aspect of the wave function is known as the Born Rule (after Max Born who first proposed it), and the mathematical framework that preserves it in QM is known as unitarity. [Fun fact: Pop-singer Olivia Newton John is Born’s granddaughter!]

Notice that 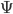$\Psi$ is a single complex-valued wave function of the collective states of all its constituent particles. This makes for some radical departures from classical physics. Unlike a system of little hard marbles, it can interfere with itself—not unlike the way the countless harmonics in sound waves give us melodies, harmonies, and the rich tonalities of Miles Davis’ muted trumpet or Jimi Hendrix’s Stratocaster. The history of the universe is a grand symphony—the music of the spheres! Its harmonies also lead to entangled states, in which one part may not be uniquely distinguishable from another. So, it will not generally be true that the wave function of the particle sum is the sum of the individual particle wave functions,

$\Psi\left ( \vec{r_{1}}, \vec{r_{2}}... \vec{r_{n}} \right ) \neq \Psi\left ( \vec{r_{1}} \right )\Psi\left ( \vec{r_{2}} \right )... \Psi\left ( \vec{r_{n}} \right )$

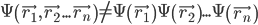
until the symphony progresses to a point where individual particle histories decohere enough to be distinguished from each other—melodies instead of harmonies.

Another consequence of this wave-like behavior is that position and momentum can be converted into each other with a mathematical operation known as a Fourier transform. As a result, the Hilbert space may be specified in terms of position or momentum, but not both, which leads to the famous Heisenberg Uncertainty principle,

$\Delta x\Delta p \geqslant \hbar/2$

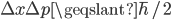
where 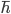$\hbar$ is the reduced Planck constant. It’s important to note that this uncertainty is not epistemic—it’s an unavoidable consequence of wave-like behavior. When I was first taught the Uncertainty Principle in my undergraduate Chemistry series, it was derived by modeling particles as tiny pool ball “wave packets” whose locations couldn’t be observed by bouncing a tiny cue-ball photon off them without batting them into left field with a momentum we couldn’t simultaneously see. As it happens, this approach does work, and is perhaps easier for novice physics and chemistry students to wrap their heads around. But unfortunately, it paints a completely wrong-heading picture of the underlying reality. We can pin down the exact location of a particle, but in so doing we aren’t simply batting it away—we’re destroying whatever information about momentum it originally had, rendering it completely ambiguous, and vice versa (in the quantum realm paired variables that are related to each other like this are said to be canonical). The symphony is, to some extent, irreducibly fuzzy!

So… the unfolding story of the universe is a grand symphony of probability amplitudes exploring their Hilbert space worlds along deterministic paths, often in entangled states where some of their parts aren’t entirely distinct from each other, and acquiring whatever properties we find them to have only when they’re measured, many of which cannot simultaneously have exact values even in principle. Strange stuff to say the least! But the story doesn’t end there. Before we can decipher what it all means (or, I should say, get as close as doing so as we ever will) there are two more subtleties to this bizarre quantum world we still need to unpack… measurement and non-locality.

Measurement

The first thing we need to wrap our heads around is observation, or in quantum parlance, measurement. In classical systems matter inherently possesses the properties that it does, and we discover what those properties are when we observe them. My sparkling water objectively exists in a red glass located about one foot to the right of my keyboard, and I learned this by looking at it (and roughly measuring the distance with my thumb and fingers). In the quantum realm things are messier. My glass of water is really a bundle of probabilistic particle states that in some sense acquired its redness, location, and other properties by the very act of my looking at it and touching it. That’s not to say that it doesn’t exist when I’m not doing that, only that its existence and nature aren’t entirely independent of me.

How does this work? In quantum formalism, the act of observing a system is described by mathematical objects known as operators. You can think of an operator as a tool that changes one function into another one in a specific way—like say, “take the derivative and multiply by ten.” The act of measuring some property 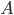$A$ (like, say, the weight or color of my water glass) will apply an associated operator 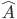$\hat A$ to its initial wave function state 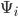$\Psi_{i}$ and change it to some final state $\Psi_{f}$,

$\hat A \Psi_{i} = \Psi_{f}$

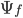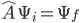
For every such operator, there will be one or more states 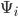$\Psi_{i}$ could be in at the time of this measurement for which 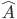$\hat A$ would end up changing its magnitude but not its direction,

$\begin{bmatrix} \hat A \Psi_{1} = a_{1}\Psi_{1}\\ \hat A \Psi_{2} = a_{2}\Psi_{2}\\ ...\\ \hat A \Psi_{n} = a_{n}\Psi_{n} \end{bmatrix}$

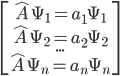
These states are called eigenvectors, and the constants 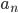$a_{n}$ associated with them are the values of 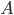$A$ we would measure if 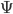$\Psi$ is in any of these states when we observe it. Together, they define a coordinate system associated with 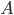$A$ in the Hilbert space that 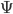$\Psi$ can be specified in at any given moment in its history. If 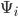$\Psi_{i}$ is not in one of these states when we measure 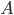$A$, doing so will force it into one of them. That is,

$\hat A \Psi_{i} \rightarrow \Psi_{n}$

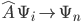
and 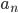$a_{n}$ will be the value we end up with. The projection of 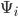$\Psi_{i}$ on any of the 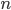$n$ axes gives the probability amplitude that measuring 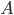$A$ will put the system into that state with the associated eigenvalue being what we measure,

$P(a_{n}) = \left | \Psi_{i} \cdot \Psi_{n} \right |^{2}$

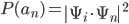
So… per the Schrödinger equation, our wave function skips along its merry, deterministic way through a Hilbert space of unitary probabilistic states. Following a convention used by Penrose (2016), let’s designate this part of the universe’s evolution as 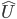$\hat U$. All progresses nicely, until we decide to measure something—location, momentum, spin state, etc. When we do, our wave function abruptly (some would even be tempted to say magically) jumps to a different track and spits out whatever value we observe, after which 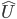$\hat U$ starts over again in the new track.

This event—let’s call it $\hat M$—has nothing whatsoever to do with the wave function itself. The tracks it jumps to are determined by whatever properties we observe, and the outcome of these jumps are irreducibly indeterminate. We cannot say ahead of time which track we’ll end up on even in principle. The best we can do is state that some property 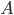$A$ has such and such probability of knocking 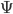$\Psi$ into this or that state and returning its associated value. When this happens, the wave function is said to have “collapsed.” [Collapsed is in quotes here for a reason… as we shall see, not all interpretations of quantum mechanics accept that this is what actually happens!]

Non-Locality

It’s often said that quantum mechanics only applies to the subatomic world, but on the macroscopic scale of our experience classical behavior reigns. For the most part this is true. But… as we’ve seen, 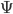$\Psi$ is a wave function, and waves are spread out in space. Subatomic particles are only tiny when we observe them to be located somewhere. So, if $\hat M$ involves a discrete collapse, it happens everywhere at once, even over distances that according to special relativity cannot communicate with each other—what some have referred to as “spooky action at a distance.” This isn’t mere speculation, nor a problem with our methods—it can be observed.

Consider two electrons in a paired state with zero total spin. Such states (which are known as singlets) may be bound or unbound, but once formed they will conserve whatever spin state they originated with. In this case, since the electron cannot have zero spin, the paired electrons would have to preserve antiparallel spins that cancel each other. If one were observed to have a spin of, say, +1/2 about a given axis, the other would necessarily have a spin of -1/2. Suppose we prepared such a state unbound, and sent the two electrons off in opposite direction. As we’ve seen, until the spin state of one of them is observed, neither will individually be in any particular spin state. The wave function will be an entangled state of two possible outcomes, +/- and -/+ about any axis. Once we observe one of them and find it in, say, a “spin-up” state (+1/2 about a vertical axis), the wave function will have collapsed to a state in which the other must be “spin-down” (-1/2), and that will be what we find if it’s observed a split second later as shown below.

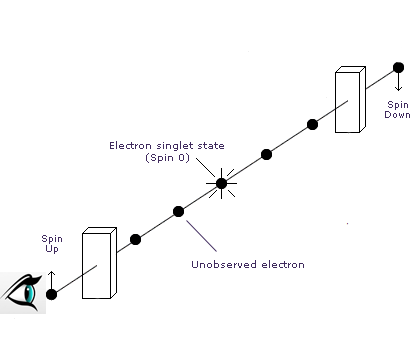But what would happen if the two measurements were made over a distance too large for a light signal to travel from the first observation point to the second one during the time delay between the two measurements? Special relativity tells us that no signal can communicate faster than the speed of light, so how would the second photon know that it was supposed to be in a spin-down state? Light travels 11.8 inches in one nanosecond, so it’s well within existing microcircuit technology to test this, and it has been done on many occasions. The result…? The second photon is always found in a spin state opposite that of the first. Somehow, our second electron knows what happened to its partner… instantaneously!

If so, this raises some issues. Traditional QM asserts that the wave function gives us a complete description of a system’s physical reality, and the properties we observe it to have are instantiated when we see them. At this point we might ask ourselves two questions;

1)  How do we really know that prior to our observing it, the wave function truly is in an entangled state of two as-yet unrealized outcomes? What if it’s just probabilistic scaffolding we use to cover our lack of understanding of some deeper determinism not captured by our current QM formalism?

2)  What if the unobserved electron shown above actually had a spin-up property that we simply hadn’t learned about yet, and would’ve had it whether it was ever observed or not (a stance known as counterfactual definiteness)? How do we know that one or more “hidden” variables of some sort hadn’t been involved in our singlet’s creation, and sent the two electrons off with spin state box lunches ready for us to open without violating special relativity (a stance known as local realism)?

Together, these comprise what’s known as local realism, or what Physicist John Bell referred to as the “Bertlmann’s socks” view (after Reinhold Bertlmann, a colleague of his at CERN). Bertlmann was known for never wearing matching pairs of socks to work, so it was all but guaranteed that if one could observe one of his socks, the other would be found to be differently colored. But unlike our collapsed electron singlet state, this was because Bertlmann had set that state up ahead of time when he got dressed… a “hidden variable” one wouldn’t be privy to unless they shared a flat with him. His socks would already have been mismatched when we discovered them to be, so no “spooky action at a distance” would be needed to create that difference when we first saw them.

In 1964 Bell proposed a way to test this against the entangled states of QM. Spin state can only be observed in one axis at a time. Our experiment can look for +/- states about any axis, but not together. If an observer “Alice” finds one of the electrons in a spin-up state, the second photon will be in a spin-down state. What would happen if another observer “Bob” then measured its spin state about an axis at, say, a 45-deg. angle to vertical as shown below?

The projection of the spin-down wave function on the eigenvector coordinate system of Bob’s measurement will translate into probabilities of observing + or – states in that plane. Bell produced a set of inequalities bearing his name which showed that if the electrons in our singlet state had in fact been dressed in different colored socks from the start, experiments like this will yield outcomes that differ statistically from those predicted by traditional QM. This too has been tested many times, and the results have consistently favored the predictions of QM, leaving us with three options;

a)  Local realism is not valid in QM. Particles do not inherently possess properties prior to our observing them, and indeterminacy and/or some degree of “spooky action at a distance” cannot be fully exorcised from $\hat M$.

b)  Our understanding of QM is incomplete. Particles do possess properties (e.g. spin, location, or momentum) whether we observe them or not (i.e. – counterfactuals about measurement outcomes exist), but our understanding of $\hat U$ and $\hat M$ doesn’t fully reflect the local realism that determines them.

c)  QM is complete, and the universe is both deterministic and locally real without the need for hidden variables, but counterfactual definiteness is an ill-formed concept (as in the "Many Worlds Interpretation" for instance).

Nature seems to be telling us that we can’t have our classical cake and eat it. There’s only room on the bus for one of these alternatives. Several possible loopholes have been suggested to exist in Bell’s inequalities through which underlying locally real mechanics might slip through. These have led to ever more sophisticated experiments to close them, which continue to this day. So far, the traditional QM frameworks has survived every attempt to up the ante, painting Bertlmann’s socks into an ever-shrinking corner. In 1966, Bell, and independently in 1967, Simon Kochen and Ernst Specker, proved what has since come to be known as the Kochen-Specker Theorem, which tightens the noose around hidden variables even further. What they showed, was that regardless of non-locality, hidden variables cannot account for indeterminacy in QM unless they’re contextual. Essentially, this all but dooms counterfactual definiteness in $\hat M$. There are ways around this (as there always are if one is willing to go far enough to make a point about something). The possibility of “modal” interpretations of QM have been floated, as has the notion of a “subquantum” realm where all of this is worked out. But these are becoming increasingly convoluted, and poised for Occam’s ever-present razor. As of this writing, hidden variables theories aren’t quite dead yet, but they are in a medically induced coma.

In case things aren’t weird enough for you yet, note that a wave function collapse over spacelike distances raises the specter of the relativity of simultaneity. Per special relativity, over such distances the Lorentz boost blurs the distinction between past and future. In situations like these it’s unclear whether the wave function was collapsed by the first observation or the second one, because which one is in the future of the other is a matter of which inertial reference frame one is viewing the experiment from. Considering that you and I are many-body wave functions, anything that affects us now, like say, stubbing a toe, collapses our wave function everywhere at once. As such, strange as it may sound, in a very real sense it can be said that a short while ago your head experienced a change because you stubbed your toe now, not back then. And… It will experience a change shortly because you did as well. Which of these statements is correct depends only on the frame of reference from which the toe-stubbing event is viewed. It’s important to note that this has nothing to do with the propagation of information along our nerves—it’s a consequence of the fact that as “living wave functions”, our bodies are non-locally spread out across space-time to an extent that slightly blurs the meaning of “now”.  Of course, the elapsed times associated with the size of our bodies are too small to be detected, but the basic principle remains.

Putting it all together

Whew… that was a lot of unpacking! And the world makes even less sense now than it did when we started. Einstein once said that he wanted to know God’s thoughts, the rest were just details. Well it seems the mind of God is more inscrutable than we ever imagined! But now we have the tools we need to begin exploring some of the way His thoughts have been written into the fabric of creation. Our mission, should we choose to accept it, is to address the following;

1)  What is this thing we call a wave function? Is it ontologically real, or just mathematical scaffolding we use to make sense of things we don’t yet understand?

2)  What really happens when a deterministic, well-behaved 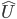$\hat U$ symphony runs headlong into a seemingly abrupt, non-deterministic $\hat M$ event? How do we get them to share their toys and play nicely with each other?

3)  If counterfactual definiteness is an ill-formed concept and every part of the wave function is equally real, why do our observations always leave us with only one experienced outcome? Why don’t we experience entangled realities, or even multiple realities?

In the next installment in this series we’ll delve into a few of the answers that have been proposed so far. The best is yet to come, so stay tuned!

References

Penrose, R. (2016). Fashion, faith, and fantasy in the new physics of the universe. Princeton University Press, Sept. 13, 2016. ISBN: 0691178534; ASIN: B01AMPQTRU. Available online at www.amazon.com/Fashion-Faith-Fantasy-Physics-Universe-ebook/dp/B01AMPQTRU/ref=sr_1_1?ie=UTF8&qid=1495054176&sr=8-1&keywords=penrose. Accessed June 11, 2017.