Having pointed out that the BVG theorem presupposes the existence of a classical spacetime, Carroll goes on to cite some evidence that the universe did not have a beginning, based on quantum mechanics (QM):
If you need to invoke a theorem, because that’s what you like to do rather than building models, I would suggest the quantum eternity theorem. If you have a universe that obeys the conventional rules of quantum mechanics, has a non-zero energy, and the individual laws of physics are themselves not changing with time, that universe is necessarily eternal. The time parameter in Schrödinger’s equation, telling you how the universe evolves, goes from minus infinity to infinity. Now this might not be the definitive answer to the real world because you could always violate the assumptions of the theorem but because it takes quantum mechanics seriously it’s a much more likely starting point for analyzing the history of the universe. But again, I will keep reiterating that what matters are the models, not the abstract principles.
First of all, some background. In QM, there's a gizmo called the wavefunction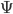 
. This is the thing that tells you what are the probabilities for any particular thing to be happening, at any given moment. It involves specifying a complex number 
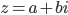for each possible configuration of the universe. Complex numbers are two-dimensional, so they have both an absolute value (or magnitude) 
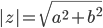and a phase (or direction) in the two dimensional plane. The square of the absolute value 
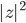gives you the probability to be in that state, while the phase (or direction) of the complex number is an additional weird extra piece of information which is special to QM. (There's some deep conceptual issues about what the wavefunction "really" means, but let's not get into that here.)
In ordinary QM, the wavefunction of the universe changes with time. If you want to work out how it changes with time, you need to know the formula for the total energy of the universe, written out as a function of the positions and momenta of all the particles or fields. Once you know what 
is, you can then use Schrödinger's equation:
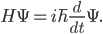
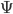is in a state with a specific energy 
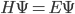(this is called an energy eigenstate), then its phase just spins around and around, at a rate proportional to the energy 
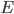divided by Planck's constant 
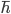. That's rather boring, since it would mean that none of the probabilities actually change at all. On the other hand, if you have a state where the energy has quantum uncertainty (meaning that it is actually a superposition of states with definite energy) then more interesting things can happen due to interference patterns between the different energy eigenstates.
So, if you know what H is (that specifies the dynamics of your theory) and you know what the wavefunction 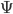is at some specific time 
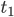, and if you assume that this theory is valid at all moments of time, then you can work out what 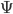is at any other moment of time, past or future. And in particular, you know what it would have been at a time 
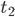which is arbitrarily earlier than 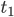is. Hence—so Carroll's argument goes—the universe cannot have had a beginning.
That's all the Quantum Eternity Theorem (QET) says. It's a little bombastic for Carroll to even refer to this as a "theorem", since it's just an elementary restatement of one of the most basic principles of QM. As Carroll said in his post-debate reflections:
For convenience I quoted my own paper as a reference, although I’m surely not the first to figure it out; it’s a fairly trivial result once you think about it.
You could still imagine that God miraculously created the universe at a given moment of time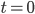 
, and that the laws of physics only apply after that moment of time. Then physics as such would have nothing to say about the actual Beginning, but only what happens after that. There's no logical contradiction in saying that, but it might make some people uncomfortable if—so far as we can tell from Science—the universe has to have lasted forever. In some ways, this is the position Christians were in prior to Modern Science, when the study of the heavens seemed to indicate that the universe just kept going on and on, like a clock that never needs winding up. Back then, Christians mostly believed there was a Beginning for philosophical reasons, or else because it said so in the Bible. We now know that the Universe developed from a simpler form, and that it has only existed in its currently observable form for about 13.8 billion years. The scientific case for a Beginning is certainly much more conclusive now than it was then, since back then there wasn't much of a scientific case at all!
But if Carroll's QET does apply, then no matter how many fireworks there were at the "Big Bang", it could only really have been the universe passing from one form to another. So is he right?
Probably not. Carroll himself states the important loophole in his reasoning, although he does it in a kind of a cryptic way so that only another physicist like me knows what it really means. Let's have it again:
If you have a universe that obeys the conventional rules of quantum mechanics, has a non-zero energy, and the individual laws of physics are themselves not changing with time, that universe is necessarily eternal.
What Carroll neglected to say during the debate, is that there's very good reason to believe that the energy of the universe is zero (if it is defined at all).
It's actually rather tricky to make precise the concept of "energy" in General Relativity. The reason is that energy is defined with respect to how things change with time, and time is a rather slippery concept in GR. There isn't just one notion of time, but rather any choice of "t" coordinate you might choose is equally valid. If there's no well-defined concept of time, then there's also no well-defined concept of energy, and the QET won't apply.
So when people do refer to energy in GR, they need to be in some type of special situation that allows them to invoke the concept. Here are the cases people talk about most often:
- If we zoom in close to one point, we can adopt a particular local inertial reference frame and define the energy of an object using that local coordinate system. But Special Relativity tells us there are several equally good notions of time, and even those are only good in the neighborhood of a single point, so this won't work for the QET.
. - If you have a spacetime which is approximately unchanging with respect to some special time coordinate "t", you can define the energy of objects with respect to that time coordinate, as long as their gravitational field is small. This is called the Killing energy, but this is also inapplicable in cosmology since the universe is not anywhere close to static (it is expanding).
. - If you have a system of objects sitting by themselves inside an otherwise empty infinite space, then you can use the notion of time defined by a clock which is very far away from the system. This is called the ADM energy, and it tells you the effective gravitational mass of the system as measured from far away. But this is also inapplicable to cosmological settings, since so far as we know the universe is not a clump of matter in an empty space.
. - Finally, if you have a closed universe (one with no boundary) then there is an unambiguous notion of energy associated with the gravitational Hamiltonian . However, it is exactly zero for all physically allowed states: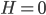
!
The conventional view of researchers in quantum gravity—with, apparently, the exception of Carroll himself—is that the same thing is likely to be true in quantum gravity. That is, instead of the usual Schrödinger's equation, the dynamics of the theory are encoded in the Wheeler-DeWitt equation:
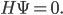
Now since tells us how 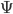changes with time, the Wheeler-DeWitt equation tells us that the quantum state does not change with time at all! That's weird, since we all know that things do change with time.
Does that mean that Zeno was right and time is an illusion? Well, we have to be very careful with interpretation here. The real reason why this happens in gravitational theories is because the choice of spacetime coordinates is arbitrary—you are free to label your spacetime points with any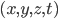 
coordinates you like: there is not one "best" way to do it. (Although I've been focusing on General Relativity, physicists expect similar issues to pop up in almost any decent theory of gravity. So long as it does not reintroduce a notion of absolute Newtonian time, there will necessarily be a "Hamiltonian constraint" saying that the only physically allowed states of a closed universe are those for which .)
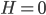So when we say that the wavefunction doesn't change with time, what this really means is that the choice of time coordinate is arbitrary. "Time" needs to be measured relative to some physical clock. There is no absolute "t" coordinate relative to which everything else moves, So, I think I would say that in this case, the QET "applies", but in a totally trivial way, and when you unpack its real meaning, it doesn't tell us anything about whether or not there was any time before the Big Bang. Thus the formalism of ordinary QM is not applicable.
To summarize, in a closed cosmology, the energy is zero, and in an open cosmology it might not even be defined. Thus Carroll's appeal to the QET probably doesn't make sense.
As I said to Carroll in the comments to his post-debate reflections:
Regarding the QET, to my mind the most conservative belief about quantum gravity is that it is—like GR—governed by a Hamiltonian constraint rather than an ordinary Hamiltonian (as in standard QM). In this setup, it’s not obvious that the QET applies.
What’s more, since there is no “absolute time” in GR, there are lots of different, inequivalent ways to evolve space forwards in time. As Wheeler put it, time is many fingered. This concept of time evolution will be much more subtle to quantize, and it’s far from obvious (to me, at any rate) that it’s forbidden for time to begin or end. In any case, this is quantum gravity, so none of us really know what we’re talking about!
And he replied:
Aron– That’s certainly a respectable point of view. It’s basically choosing the option that the energy is zero, which is definitely a possibility. And if that does turn out to be the case, time can certainly “end,” but in a very funny sense, since “time” was only emergent to begin with.
But the other option, that the energy is not zero and the ordinary time-dependent Schrödinger equation applies, is at the very least equally reasonable (perhaps more so). Our best-understood example of quantum gravity is the AdS/CFT correspondence, where the theory is most carefully defined in terms of the Hamiltonian of the boundary theory — in which perfectly conventional Schrödinger evolution applies. My suspicion is that quantum gravity will work similarly in other cases as well. But as you say, it’s quantum gravity, so we’re allowed to speculate but not allowed to act like we know the answer.
AdS/CFT is a famous duality between an ordinary QM theory (the CFT) and a gravitational (string) theory with a negative cosmological constant. In this case, there is a well-defined nonzero , but that is because you have a bunch of matter sitting in an otherwise empty AdS space, so you can use the ADM definition of the Hamiltonian. (This duality tells us very interesting things about general aspects of quantum gravity, but it probably doesn't apply directly to our own universe, which has a positive cosmological constant, among other considerations.)
GR predicts (A) that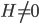 
for matter in AdS space, and (B) that 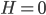for closed universes. It doesn't make any sense to me to say that because string theory agrees with GR about (A), it probably disagrees with GR about (B). To me, the most conservative thing to say is that both of these facts continue to be true. Furthermore, case (B) is far more likely to describe the real universe than (A) is.
Although, as we both said to each other, no one really knows for sure how the correct theory of quantum gravity is going to be formulated. Of course, there is nothing wrong with Carroll putting forward his personal opinion in the debate—I can hardly complain about that after Craig put forward my opinions! But I think he could have been more clear that it was his personal opinion, and that, given more "conventional" beliefs about quantum gravity, the QET probably can't be applied in cosmological settings.
[9/22/14: a few minor wording changes—AW]
Aron,
Well done again, Sir.
Just like to make a few observations and ask a few question.
In the Carroll-Craig debate, Carroll said in his opening speech . “I want to argue that naturalism is far and away the winner when it comes to cosmological explanation. And it comes down to three points. First, naturalism works—it accounts for the data we see. Second, the evidence is against theism. Third, theism is not well defined.” Having read your Blogs and your responses on to readers’ questions, I have to say that the totality is a devastating refutation of Naturalism. Isn’t it interesting that energy isn’t such an easy thing to define after all? Which brings me to Carroll’s special pleading of non-zero energy of the universe to make the argument of an eternal universe work.
Aron, Don’t we need a model that explains why the energy is non-zero instead of assuming the condition exists? Is this assumption necessary to make the mathematics "manageable".
It seems that until some new theory supplants the Big Bang and is supported by observations, I think the notion of a beginning of the universe and time remains unrefuted.
Zero energy (the positive energy from matter exactly balanced by negative energy from gravity) is taken to mean the universe consists of nothing. In physics “nothing” is “something” as your blog, “A Universe from Nothing? Posted on December 7, 2012, “A Universe from Nothing”, and David Albert’s review of the book in the New York Times, March 23, 2012.).
Why do so many smart physicists continue to write this fallacy?
Good stuff! Would love to hear more about some pre-Big Bang models that are aimed at getting around the BGV such as Emergent Models and Aguirre-Gratton, and whether we know anything that falsifies them.
Thanks
Craig responded in part to Carroll’s argument from the QET for an eternal past by saying that the QET tells us that if there is a prior moment then we can describe that moment, it does not tell us whether that prior moment existed (http://www.reasonablefaith.org/does-quantum-mechanics-indicate-an-eternal-universe). Is this correct? (Forgive me if you have answered this in your essay above and I just missed it.)
Dennis,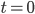
. So only times with 
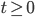exist.
It's really an ambiguous question. Suppose that the universe began at a particular moment of time; call it
Now the basic premise of Carroll's QET is the Schrodinger equation, which I wrote in the post above. If we say it's a "law of nature" that the Schrodinger equation has to be true for all values of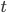
, then there must exist times 
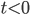for it to apply to. On the other hand, if we phrase the "law of nature" so that it is only valid at moments when there is time, then there is no contradiction with it only applying at times 
.
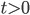I think I addressed this issue in the paragraph beginning "You could still imagine that God miraculously created the universe at a given moment of time t=0, and that the laws of physics only apply after that moment of time."
So I agree with St. Craig that there's a way to phrase things where a beginning of time is consistent with the Schrodinger equation, but I don't quite agree with his phrasing when he says that "in order to know whether there is such a[n earlier] moment we must look to empirical evidence." If the premises of the QET are true (though I think they probably aren't) then there is at least an answer to the question of what would have occured before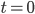
if one continued to apply the Schrodinger equation to those earlier times, and I see no way that purely empirical physics considerations could rule out those times actually existing.
Aron,
I have just been listening to the Craig Carroll debate where Craig stated that you have formulated, " a new singularity theorem". Is it the case the you have done so and could you direct me to the journal where it is published. Was the publication peer reviewed?
Thank you
Dear GS,
Yes, it's true. The article in question is published in Classical and Quantum Gravity, which is a peer-reviewed, high quality journal. (However, you might be surprised how often wrong stuff makes it past peer-review! It's not a magic bullet by any means.) It was also highlighted by one of the CQG editors.
You can find the article online at the journal webpage or on the arxiv.
My article extends the Penrose singularity theorem to situations involving quantum fields, which can have negative energy densities. The main assumption is that the Generalized Second Law of thermodynamics holds for all causal horizons, for which there is significant theoretical evidence. There's also some other technical assumptions discussed in the article. I also have a section speculating that these assumptions might be applicable to full quantum gravity, but this can't be proven since nobody understands quantum gravity.
I've also described aspects of the article in parts II and VI of this series, and also in a Scientific American blog post.
Aron,
Thanks for this article. I found it after reading Craig's question of the week article.
Since we are discussing Quantum Physics, I would really love to hear about your views on the orthodox or copenhagen interpretation of Quantum Mechanics.
I'm not sure if you have heard, but there is a you-tube channel called "InspiringPhilosophy" and he is an idealist Christian who uses some quantum mechanical findings to infer the existence of a mind (God).
I know I may be asking for too much, but please allow me to beg you to watch some of the videos in this playlist of his and give me your own personal opinions on his work? I really would love the input of someone with your expertise on this!
https://www.youtube.com/playlist?list=PL1mr9ZTZb3TViAqtowpvZy5PZpn-MoSK_
One video you may especially like is the one called "the introspective argument" or "Quantum Physics debunks materialism".
I really hope you view these!
In Section III, you mentioned a contracting and then expanding (but, I'm assuming, non-cyclic) universe as an alternative of infinite age to the one hypothesized as expanding from a beginning. A long thread on the Physics Forum mentioned that such a "one shot" contraction to a bounce into expansion was characteristic of those cosmological alternatives that rely on quantum mechanics rather than relativity. I find any beginning to everything inconceivable, but, to me, it would be simpler to say that the expansion arose from a state lacking any averaged tendency toward either. Why the takeoff roll through a contracting phase?
I'm out of my league here, so any needed correction/elaboration to the following would be appreciated...
If I'm reading this right, Carroll's argument for QET is heavily dependent on AdS/CFT, which as Aron pointed out, probably doesn't apply to our universe anyway. If so, it's interesting that AdS/CFT has been running afoul of real-world data as well. Over at Backreaction Sabine Hossenfelder discusses recent attempts to model LHC heavy ion collision data with it (specifically the impact of quark gluon plasma viscosity on the hadronized jets emitted by such collisions). As luck would have it, the AdS/CFT predictions for these runs do not match the data either quantitatively or qualitatively. Add to that the fact that LHC Run 1 has taken us well into the regime where we should've found ample evidence of Minimal SuSY superpartners by now, and so far it would appear the real-world hasn't been kind to AdS/CFT or its M-theory underpinnings. I would imagine this doesn't explicitly disprove Carroll's version of QET, but in the very least it ought to put the burden of proof squarely on his shoulders.
Of course, explorations of M-theory and AdS/CFT are still in their infancy, and I don't know how relevant any of this is to cosmological questions. And although M-theory does require some form of SuSY it need not be the Minimal version. But it seems to me that these things don't bode well for AdS/CFT, M-theory, QET or M-theory-based multiverse scenarios as viable answers to fine tuning. Unfortunately, one of the problems with M-theory is that it's pliable enough to accommodate virtually any dataset thrown at it, rendering it virtually untestable for the foreseeable future. (No doubt, this is why Carroll and others are crusading for the elimination of real-world testability as a requirement for science). Is there anything I'm missing here...?
In any event, LHC Run 2 is now under way and is slated to push into the 13-14 TeV collision range. If it fails to turn up a gluino or other SuSY superpartner it'll be interesting to see how Carroll and other M-theory true believers respond. 50 bucks says that within a month of run completion there'll be multiple papers at Arxiv predicting that Run 3 will turn up the desired evidence, and they'll be even more convinced that QET and the M-theory multiverse are on a more solid footing than anything real-world-facts folks could ever come up with... especially if they believe in God. ;-)
Ed,
You could try to construct a universe which remains in a static configuration for a long time, and then starts to expand, but that raises some troublesome questions. For example, if the static universe is really unchanging with time until it decays to the expanding phase, and if it has some finite probability to decay at any time, then it is impossible for it to have been in the static phase for an infinite amount of time. (Alex Vilenkin has some talks and papers discussing models like these.)
Also, it's generally very hard to stabilize such universes. For example, Einstein constructed a static universe where he balanced the attraction due to matter's gravity with repulsion due to a cosmological constant, but this turns out to be unstable. If it shrinks a little bit, there is a runaway contraction to a singularity, and if it grows a bit, there is a runaway expansion.
Whereas de Sitter space is a very natural solution to GR which contracts and then expands.
Scott,
I think it's important to sharply distinguish between:
1) string theory or AdS/CFT as an effective phenomenological model for the strong interactions
2) string theory as a candidate theory of quantum gravity at the Planck scale,
and
3) string theory or AdS/CFT as a (probably) mathematically consistent structure, serving as a toy model for quantum gravity ideas, some of which may be useful even if the real world is described by a different theory of quantum gravity.
There's lots of good (mathematical) evidence for the validity of (3), which is enough I think to motivate a nonzero Hamiltonian in asymptotically AdS spacetimes. But in that respect AdS/CFT is no different from classical GR, and classical GR predicts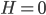
in a closed universe.
That string theory is valid at the Planck scale is a plausible hypothesis, supported by the great difficulty in constructing other good theories of quantum gravity, but it is not supported by any kind of direct experimental evidence. And as you say, the LHC evidence for things like low energy supersymmetry is weak. (Supersymmetry could be broken at higher energy scales, which would be fine so far as string theory is concerned, but makes it no longer useful for explaining the fine tuning of the Higgs mass.) In any case, this would require finding solutions to string theory with a positive cosmological constant, so AdS/CFT would not directly apply although it may still give clues about various questions like e.g. do black holes lose information?
Whether or not AdS/CFT is useful for describing the phenomenology of quark-gluon plasmas is a completely separate question, which stands or falls independently of the other things. (It uses the "CFT" side of the duality, not the "AdS quantum gravity" side.) Some of the CFT's which have useful holographic duals are qualitatively similar to QCD in certain respects, but there are also a lot of important differences (lots of supersymmetry instead of none, a very large number of colors instead of 3, the quarks interact with the gluons differently than in QCD, etc.) So there was no good reason to expect anything more than qualitative predictions for heavy ion collision physics, and if it turns out that the fit is terrible, I don't think that's particularly surprising, or evidence against the consistency of AdS/CFT as a mathematical structure.
Aron, thanks... this spoke directly to my questions. As you might have guessed from my comments, while the AdS/CFT issues with modeling QCD interactions seem significant to me, I wasn't sure to what extent they're relevant to quantum gravity, cosmology and M-theory in general, if at all. To be honest, 3) never occurred to me, although it should have since AdS/CFT is useful for making many otherwise intractable problems solvable and toy models are a lot more useful than many folks realize. I didn't realize that M-theory requires Minimal SuSY to explain the fine tuning of the Higgs mass either.
As always, great stuff Sir! Since last fall I honestly I think I've learned more theologically relevant physics and philosophy from this blog than I had in my entire life before then. And speaking of M-theory and the Higgs, I'm anxiously awaiting your series on fine tuning and the multiverse. I'm planning on an essay or two of my own covering some of that as well. If I finish mine before you do yours I may hit you up for a sanity check. Thanks again, and keep up the stellar work! :-)
Btw, for the record I agree that string theory (or more specifically M-theory) is very plausible, and perhaps even as they say, "the best game in town" for a potential quantum gravity theory. The framework is elegant and in theory at least predicts things that might physically exist (e.g. extra dimensions, compactified Calabi-Yau spaces, and the associated vacua). But it's so fluid that it can be made to agree with/predict virtually anything, and I don't see how we're ever going to get beyond that without probing on distance scales comparable to those of its compactifications. Last time I saw any estimates of such, this would require an LHC roughly the diameter of the solar system, which needless to say ain't happening any time soon. If there's another way to get useful predictions out of any string theory I have no idea what they would be, and as near as I can tell no one else does either. And much as I love the inflationary paradigm and hate to admit it, in the absence of any useful candidates for an inflaton (beyond some generic scalar field) the same can be said for it as well (although to be fair, BICEP2 + Planck does appear to have ruled out a lot of inflationary models, specifically those involving higher scalar-to-tensor ratios).
My real complaint isn't with M-theory per se, but with folks like Sean "Can-I-Build-A-Model?" Carroll who insist that none of this matters. As long as we can dream up any old scenario that can be stretched to fit whatever we see (or even can't), anyone who thinks twice before jumping on the M-theory bandwagon risks being labeled as an anti-science obscurantist. It also annoys me that they unquestioningly assume that Inflation = Eternal Inflation + String Landscape + Anthropic Multiverse. While it is true that most inflationary scenarios are eternal, not all are... and in fact, most of those that survived BICEP2 + Planck aren't (e.g. the Starobinsky model). And whatever the final quantum gravity theory turns out to be, unless it actually takes us beyond the Standard Model (which, I might add, virtually nothing observationally supportable to date has), even eternal inflation will only yield universes similar to ours, which won't do much to address all those fine-tuning issues they so quickly side-step. It seems to me that whether Carroll et al. admit it or not, to them the real appeal of all this is less scientific than "a-theological."
But now I'm off topic. I'll save further such thoughts for the much-anticipated Fine-Tuning/Multiverse series... coming soon to a blog near you! :-)
Pingback: Did the Universe Have a Beginning? – Carroll vs Craig Review (Part 1) | Letters to Nature
This seems to be as good a place as any to ask a question about closed universes.
See, in a lot of popular science books, they teach you that an "open" universe is one where space is infinite, saddle-shaped, and keeps expanding forever; a "flat" universe is infinite, plane-shaped, and the rate of expansion eventually peters out to zero; and a "closed" universe is finite, sphere-shaped, and eventually contracts in a big crunch. They then talk about the cosmological constant and "dark energy," which make our universe expand at an accelerating rate, something that doesn't fit the taxonomy of possibilities for the universe's topology, and which they do not relate back to that taxonomy in any way.
Can a universe with lots of dark energy be a closed universe? Will a closed universe with dark energy keep on expanding and accelerating, or will it eventually collapse in a big crunch like a "normal" closed universe? Is the three-type Taxonomy only relevant given certain energy conditions? (Strong/weak/null)
Oh, and I almost forgot:
are there any good reasons to think that the universe is closed in the first place, other than Kalam-esqe arguments against actual infinities?
David,
I responded to your question here.
Pingback: L’argument du Kalam [Argument cosmologique] – Défense du théisme
Aron,
You write
"You could still imagine that God miraculously created the universe at a given moment of time t=0, and that the laws of physics only apply after that moment of time."
Why does it needs to be imagined? Surely
i) Creation of the universe is not an empirical event for
a) It is not observable even in principle.
b) Physics deals only with the correlation of configuration of matter at time t to the configuration at a
different time. This is all the equations and theories of physics are about. The creation of the matter is
outside the remit of physics.
ii) The laws of physics apply in the universe that exists. Thus there is no sense in which any theory or law of physics could describe the actual creation of the universe.
As you note, the Big Bang scenario, though often wrongly understood as describing creation of universe, does nothing of the sort.
But still, this clear picture that the creation of universe is an non-observable event in principle, and thus outside the remit of physics, this clear picture is confused in a lot of people including cosmologists.
Hello,
I enjoy reading your responses to the Carroll v. Craig debate.
For this part though, I don't think Carroll was at all trying to say that QET was an accurate model of our universe or demonstrated that our universe existed before the Big Bang. I believe the point Carroll was trying to make was to counter Craig's assertion that it is impossible for a natural universe to be infinitely old. Carroll was attacking this premise by trying to show that the QET could be used to construct a "plausible" natural universe that does not have a beginning and will last forever. No God required. He immediately says "Now this might not be the definitive answer to the real world because you could always violate the assumptions of the theorem but because it takes quantum mechanics seriously it’s a much more likely starting point for analyzing the history of the universe."
That was my take when I listened to the debate because he announced right off that he was going to challenge the first premise which was that the universe needed some transcended cause
Thank you,
Matt
Hi @Eddy,
As you said, Carroll wasn't arguing that QET is an accurate model of the universe, but responding to Craig's claim that a natural universe cannot be past/future infinite. However, he never actually did address it. Craig has made many cosmological arguments against our universe actually being past-infinite, but his arguments for the physical impossibility of any such universe are based on the logic of infinities and paradoxes like Hilbert's Hotel. Whatever strengths or weaknesses they may have, those arguments are ultimately philosophical. They have nothing whatsoever to do with physics or cosmology, including QET.
Like most if not all atheist scientists today, Carroll's worldview is built entirely on scientism. In its more extreme forms, scientism asserts that Science alone (note the capital "S") is, quite literally, the only source of knowledge there is, and as such, the last word on virtually any question that could ever conceivably be asked about anything whatsoever. In his case, the Holy of Holies is Physics. Unlike many atheist physicists today, Carroll does have a background in philosophy having minored in it as an undergrad. As such, he avoids most of the philosophically illiterate foolishness preached by some of his colleagues. But even so, he still seems to view philosophy as nothing more than a handmaiden to Physics that can be summarily dismissed at will. The only question that matters, he claimed, is "can I build a model...?" Everything else is meaningless... because, he said, "Our metaphysics must follow our physics. That's what the word metaphysics means." [The last statement is not only false but largely so for reasons that are downright entertaining. But that's a topic for another day].
So, Craig presented Carroll with philosophical arguments for the impossibility of physical infinities... and he responded by begging the question. Physics is the last authority on any conceivable question. --> Infinite QET toy models can be imagined... whether they look anything like the real world or not. --> Therefore Physics trumps philosophy. --> Which makes Physics the last authority on any conceivable question.
He's arguing in a nice, tidy circle. :-)
Hello Scott,
Well I don't think that is what Carroll was trying to say. I don't think Carroll was saying (or would say) physics was the final say on "any conceivable question", but he does believe (and I as well) that the formation and evolution of the universe is well within the wheelhouse of physics. If someone is going to make philosophical assertions about the beginning of the universe, physics has something to say about it. And if empirical evidence or observations do negate a philosophical premises, then yes, science tends to trump philosophy. I think that is pretty evident. So Carroll was trying to demonstrate that the philosophical premise that the universe came into existence, and therefore needed a transcendent cause, is not well supported by our current understanding of physics and cosmology. In fact, based on this current understanding we can have universes who are infinitely old or have come from nothing. You may not agree with the methodology, but that’s your own personal choice. So I don’t think Carroll’s argument was any way circular.
Take care,
Matt
Hi @Matthew,
My apologies for the long, rambling comment. I'm afraid pithiness has never been one of my strong points. :-) But you've raised some valid points and I wanted to do my best to give you a response that's worthy of them. Please note that the topics below are far too large to be treated in any depth here, so I hope you'll forgive me for only be able to offer a lengthy fly-by. I've provided links to more in-depth treatments wherever I could.
For the most part, I agree with your last, but with a few significant caveats. First, I do agree with Carroll, and you, that the formation and evolution of the universe are well within the wheelhouse of physics, and if philosophical assertions are made about its beginning, then physics definitely has something to say about it. I also would agree that if robust observational evidence ever does negate a philosophical premise, then, in that case, Physics trumps it. But this is largely academic. Physics and Philosophy are complementary disciplines, not oppositional ones. They certainly do inform each other, but they come at topics like these from different perspectives. Only in the rarest of circumstances does Physics have occasion to trump any philosophical premise. The number of times that's arguably happened since the Enlightenment can be counted on one hand, and virtually nothing that was addressed during the Carroll/Craig debate falls within that realm (more on that in a moment). Indeed, the very idea of an either/or God vs. Physics dichotomy reflects a fundamental misunderstanding of both. This is addressed in more detail in this post of mine and this series by Aron. I would recommend both to you.
Second, while I do find the kalam cosmological argument compelling, I also agree that it's not without holes and I think Craig is unnecessarily weakening his position by tying himself to it so strongly. To that extent, Carroll has a valid complaint. But that said, although Physics does speak to whether the universe began to exist or not, the question of whether such a beginning requires a transcendent cause is not one Physics itself can speak to (again, I refer you to the posts just linked). It also moves the goal posts. Your original comment was in regard to whether it's impossible for a natural universe to be infinitely old. Though related, that's actually a different question, and one for which Craig offers philosophical arguments that valid or not, Carroll did not address. As Aron clearly demonstrated in this post, QET doesn't speak to either of these questions at all.
Which brings us to the next point... Stated this starkly, I imagine he'd deny it (sincerely, I believe). But Carroll seems to think that as long as his fertile imagination can dream up a mathematically consistent toy model that superficially accounts for some aspect of the natural world, then demonstrable or not, that alone invalidates virtually every other comment or question on the matter that any thinking person could ever conceivably raise. For instance, in the debate he tells us that,
Um, no, that is not what we should ask. What we should ask is, "Can I build a model that accounts for all current observational data and is simpler, more broadly-based, and more robustly predictive than any of its competitors? Toy models of the sort Carroll routinely invokes rarely rise to even one of those bars, much less all of them. To wit, he goes on to say,
Um, no, it has not been done. The no-boundary model he refers to is based on a semiclassical boundary constraint that may or may not reflect a true underlying quantum gravity theory, it requires elaborate and arbitrary mathematical jury-rigging, the end result of which may not even have physical significance. Even if we waive all that, the universe it yields has less than one chance in a Penrose number of resulting in anything other than one so wildly different than the one we actually live in that we couldn't exist. Needless to say, we do exist. :-)
Then there's the QET itself. As Aron recounts in the post, when he pointed out to Carroll that the universe will be governed by a zero-energy Hamiltonian constraint rather than the ordinary Hamiltonian QET is based on, he responded by pointing to the AdS/CFT correspondence as "our best-understood example of quantum gravity," and an example of a non-zero-energy model that to him is "at the very least equally reasonable (perhaps more so)." AdS/CFT is a duality within certain classes of string models that maps a few simple conformal field theories onto an anti-de Sitter space (the AdS part). Not only is it a toy model that doesn't come anywhere near to accounting for the Standard Model, as already noted, the string landscapes it's based on are virtually untestable even in principle. To call this "an example of quantum gravity" (much less our best one) is naive at best, and even if that weren't the case it has one really big problem... it's verifiably false. The 2011 Nobel Prize in Physics was awarded to three physicists who demonstrated observationally that we don't live in an AdS universe.
BTW, speaking of "empirical evidence or observations," it's worth noting that Carroll is a vocal proponent of a school of thought known as post-empiricism which states that apart from a superficial agreement with observation, testability has no place in Physics. If a model can be made to fit current observations then it is de facto true, and attempts to put it to any test are at best, a waste of time. Post-empiricism is popular among string theorists for the obvious reason--because string landscape/multiverse theories are not only untestable even in principle, but fluid enough to be stretch-fit to virtually any observation that could ever conceivably be made. Under post-empiricism they win by forfeit simply because they're beautiful... even though they make no meaningful predictions of any kind whatsoever. Needless to say, such ideas have alarmed the larger scientific community, and led to calls for more dialogue between physicists and... [wait for it]... philosophers. Carroll dismisses all of this as the falsification police not allowing him to "demand ahead of time what kind of theory correctly describes the world" (my emphasis)--as though robust predictions and observational tests are an unreasonable bar for science to have to rise to.
--------------------------------------------------
Ultimately, I agree Carroll wasn't trying to claim that physics is the final say on all questions--at least, not during the debate. But to suggest that this sort of toy model hand-waving gives us permission to dismiss nearly 3000 years of Metaphysics and Theology as "extra metaphysical baggage" is textbook Scientism at its worst and takes hubris to a whole new and terrifying level. So much so, that a term has even been coined for it: physics envy.
My "personal choice" of methodology has nothing to do with any of this. Physics tells us only that it's possible to construct mathematically consistent universe models that are infinitely old. Whether those models or their formal infinities translate to the real world without breaking down, or whether the universe actually is infinitely old is another matter altogether. "I can build pretty toy models --> Therefore God isn't needed --> So my toy models trump Metaphysics and are de facto true..." If there's a better example of circular reasoning I have no idea what it would be.
And as for universes "from nothing," not only is that a misunderstanding of Physics, it's a failure even to grasp the English language. For more on that, see this post of Aron's and Luke Barnes' posts Of Nothing and More Sweet Nothings. Ed Feser has also weighed in on the topic from a philosophical standpoint a number of times, including here and here.
Best.
Hello Scott,
I am trying to make sure I hit your main points and don’t stray too far off the topic, so let me know if I missed anything or if you feel something is unrelated.
From my perspective, both the KCA (Kalam Cosmological Argument) and physics based explanation for the beginning of our local universe are very speculative. I think we can both agree on that? Craig offers a philosophical argument, and I believe Carroll then attempts to address the argument from a physics perspective. Neither of them are very good largely because both sides have to make a number of assumptions. As you say “Physics tells us only that it's possible to construct mathematically consistent universe models that are infinitely old.” Correct, and Craig is saying it’s possible that the universe is finitely old based on certain philosophical arguments – which he tries to reinforce with scientific data. As we have discussed, physics can trump philosophical premise, so what Carroll is essentially saying is that Craig’s philosophical premises for the KCA are not well supported by our current understanding of physics and therefore trumps his philosophical argument (you may or may not agree that he was successful in this regard). You say that Carroll did not answer all of Craig’s philosophical arguments; I am not sure which one specifically you are referring to and I don’t think Carroll should be answering philosophical arguments – he is not a philosopher. You probably will agree that Carroll is weak in the philosophical realm . I think Carroll’s intent was to undercut the philosophical arguments in general by saying the premises for the KCA are incorrect – largely by saying that we have no solid evidence that the universe had to begin. You mention that physics cannot comment on the need for a transcendent cause, but I believe it can – if physics finds that the universe is infinitely old, that eliminates the need for a transcendent cause.
As for the “universe from nothing” I agree, Krauss especially, plays word games, and either he is pretty obtuse when apologists use the word “nothing” or he is intentionally playing word games. I am not going to say that I am a proponent of the universe from nothing theory, and I would say that is the least likely explanation.
I don’t believe Carrol thinks that his toy models = no god. He even says at the end of the debate that people don’t typically base their belief in God on Cosmology – and I believe he even mentions that’s not why he ultimately stopped believing. Craig would say the same thing about the KCA, and I believe he even said that if science knocked down the KCA, and fine tuning argument, he would still believe in God. Which, I believe for Craig to offer these arguments as proof for God is a little disingenuous because they aren’t actually a foundation for his belief . However, if science did point to a “transcendent” cause, I believe it would force Carroll to change his position. Obviously, the evidence would have to be pretty robust and I am not sure what form that evidence would take except perhaps if we exhausted all science and we still couldn’t answer how the universe started.
You seem to take umbrage at Carroll tossing aside Aristotelian causation. I would agree with you on this point. I don’t think his comments were well supported and from my perspective I think he would have a more effective if he didn’t mention this at all.
When I mention preferred methodology, for some people mathematically based models are more convincing than philosophical reasoning. These models really only serve as a demonstration that infinitely old universe cannot be ruled out by science. As we determine a better theory to explain gravity, and gather more data, this could go either way. I believe the prevailing thought within the cosmological community is that we live in some sort of multiverse but the age, size and extent is completely unknown (I could be wrong here). At each step we have been surprised at the size of the universe we live in. At first we thought we were at the center with the sun orbiting the earth. Then we figured out the model of the solar system, then the stars, then our galaxy, then another galaxy, then millions of galaxies, and now it’s in the hundreds of billions of galaxies with hundreds of billions star within each. Thought it’s a bit of an assumption, it seems that finding a multitude of universes would not seem unlikely.
Take care,
Matt
Hi Matthew,
Again, I mostly agree. A couple more quick comments though (or at least, quicker than my last :-) )...
First, to answer your question, one argument against physical infinities that Craig has relied heavily on is Hilbert's Hotel, which purports to show that any attempt to physically instantiate an infinity will run afoul of absurdities that infinite mathematics alone cannot capture. Whatever strengths or weaknesses one thinks that argument has, the QET argument is not a valid response to it. It is itself based on a toy model mathematical infinity, and as such, merely begs the question against that argument. But that said, I do agree that Carroll brought it up primarily as a response to the first premise of the Kalam argument, and to that end, if it didn't suffer from the fatal flaws addressed in this post and comment thread it would've succeeded in that.
Second, it actually isn't true that an infinitely old universe would eliminate the need for a transcendent cause. The traditional cosmological argument (which personally, I think Craig should rely on more than the Kalam) is based entirely on simultaneous causes in the present moment (which the Scholastics referred to as essential causes and physicists refer to as interactions). It makes no reference whatsoever to time-ordered (or accidental) causality even from a few seconds ago. This is also discussed at length in the post of mine I linked above, with further source material.
In fact, St. Thomas Aquinas, who arguably developed the argument better than anyone else in history, famously argued that it wasn't possible to prove that the universe isn't infinitely old. He believed it wasn't, but he took that on faith based on the Bible (which he had other reasons for considering authoritative). Apart from that, however, he believed that observation and rational arguments alone could not demonstrate it. Popular versions of the argument based on a temporal first cause are modern caricatures of it that continue to persist largely because secular critics find them easier to respond to than the actual one.
Best.
Hello Scott,
I am probably sounding like a broken record at this point, but I don't think Carroll's intention was at all to say that the QET theorem is any way like our universe or even a possible explanation of our universe. When I go back and read the transcripts, I see how someone might get the impression that is the case. Carroll is simply refuting the argument that it is not impossible for a natural universe to be infinite - challenging the BVG Theorem that WLC typically relies on to say an infinitely old universe is impossible.
As for the rest of your response I believe - from a cosmological perspective - relies on a great deal of speculation. It certainly is an interesting thought experiment to consider if the universe is infinitely old or not. I suspect it is probably timeless. Maybe one day soon we might have a complete theory of gravity and we could have a little bit better insight into the formation of the universe before the Big Bang.
Regards,
Matt
Aron, thank you for writing this. It has now been six years since the debate. I finally decided to write my own analysis of the debate. It's called "Sean Carroll's Dishonesty: The Debate of 2014." I mentioned this blog post. You can read it at https://freethinkingministries.com/sean-carrolls-dishonesty-the-debate-of-2014/
Dear Aron!
You write the following:
“You could still imagine that God miraculously created the universe at a given moment of time t = 0, and that the laws of physics only apply after that moment of time.”
I’m a bit confused about it, since I thought that Relativity theory does not allow an absolute scale of time. How do we choose the moment of time t=0 then?
Mr C
It's just an arbitrary convention. Pretend I said "...created the universe at a given moment of time (let's call this t = 0), and that..."
Dear Aron,
Sure, I understand that the moment is chosen just for convenience. However, if we say that, for instance, the Earth was created just five minutes ago, when were created other planets, the Sun, and all the stars? I guess, it's a purely physical question, since I also don't really understand how people define the age of universe with regard to GR. There's no absolute scale of time, right? That's the basic source of my confusion.
I'll be glad if you clarify this moment.
Mr. C
It's a good question. (But I'm going to ignore the hypothetical about the universe being created 5 minutes ago, and give the answer for our best models of cosmology.)
In general, there are many different possible notions of the "time" coordinate in general relativity, and there is not usually a compelling reason to pick out one in particular.
However, it is an observational fact that, at very large distances, the universe appears to be homogeneous (the same in every place) and isotropic (the same in every direction). This obviously isn't true at the scale of solar systems, or galaxies, or even clusters of galaxies (since these involve clumps of matter) but if you zoom out to even bigger scales, then you can ignore the clumpiness and treat the density of matter as being uniform.
In this approximation, and ONLY in this approximation, one can define a specially privileged time coordinate called "cosmic time". This is defined to agree with the time that would be measured by clocks that are at rest relative to the uniform matter (called the "cosmic rest frame").
So when cosmologists say that the Big Bang happened about 13.8 billion years ago, they mean in this particular coordinate scheme. (Although there is a small amount of ambiguity due to the fact that the uniformity assumption isn't perfect, I believe this ambiguity is small compared to observational error, so it is usually ignored.)
Dear Aron,
Many thanks for your explanation! I was trying to make sense out of Omphalos hypothesis with regard to GR (I’m not a creationist, btw, I was just investigating a pure logical possibility), and the notion of time confused me quite a bit.