You've probably heard that time is the fourth dimension. What does it mean? It should seem rather fishy that time should be the same sort of thing as a spatial dimension. We all know that you can only go in one direction in time—towards the future! Time is measured in seconds, space in meters, etc. It turns out though, that time can be thought of as the same sort of thing as space, but not exactly: there's just one tiny change that makes everything turn out different.
Let's start with two dimensional boring old Euclidean geometry of the sort one learns about in high school. It's called two dimensional because you can specify the location of a point using two numbers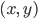 
. Now the most important equation—from which everything else about geometry follows—is the Pythagorean theorem. This allows you to compute the distance 
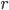between any two points 
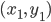and 
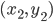. If we define 
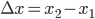and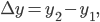 
then we can think of 
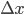and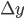 
as the sides of a right-angled triangle. Then the Pythagorean theorem says that then the distance is
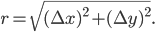
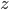coordinate: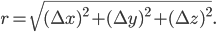 
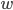since we're out of letters at the end of the alphabet) and then write down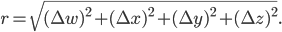 
What has not yet arrived is spacetime. Each of these dimensions are all exactly the same (it doesn't matter which one we call "first", "second", "third", or "fourth" because of rotational symmetry). There is no notion of past or future. To get a time coordinate, we have to do something to make it special. And what we do is very simple, we just put in a minus sign:
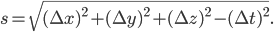
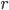as the separation 
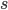, but that's just a change of notation. What you should be noticing instead is how similar this equation looks to the last one. In fact, just as all of Euclidean geometry essentially follows from the Pythagorean theorem, so all of what's called Special Relativity, or the geometry of Minkowski space 
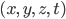essentially follows from this one equation. (Minkowski was the name of Einstein's math teacher, who first pointed out this way of understanding relativity.)
Now, what is the effect of this minus sign? It turns out that it changes things rather a lot. In Euclidean geometry, the thing inside of the square-root is always positive. But because of the minus sign, the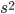 
of two different points can be either positive, negative, or zero:
- If
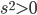, then its square root represents the distance between the two points, just like in Euclidean geometry. In this case we say that the two points are "spacelike" separated. - If
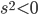, then the thing under the square-root is negative, so when we take the square-root we get an imaginary answer. Fortunately, that's okay! We just flip the sign of the thing under the square root, and intepret it as a duration instead of a distance. In this case the two points are "timelike" separated. - If
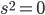, then there is neither distance nor time between the two points. In this case, we say that the two points are "lightlike" separated. That's because rays of light (in a vacuum) travel along paths whose points are lightlike separated—in a sense, because they are travelling equally in space and time, but they experience no time or distance as they travel.
I should say that I'm using units here where the speed of light (normally called 
) is equal to one. That means that e.g. if we measure time in seconds, we have to measure space in light-seconds (the distance light travels in one second). Otherwise, the beautiful equations would get all cluttered up with 's flying all over the place.
We're used to dividing up time into three parts relative to ourselves: past, present, and future. The present is just an infinitesimal sliver, so in a sense this division is into two parts: points to the past have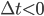 
compared to you, while points to the future have 
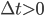compared to you.
However, special relativity tells us you have to chop up spacetime in a more complicated way. Bearing in mind that you each live in a particular place as well as a particular time, you can chop up spacetime into three different regions. The future is points that are timelike separated to you and have 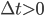; these are the points of spacetime that you can affect. The past is points that are timelike but have 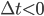; these are the points that can affect you. Then there is elsewhere, the points that are spacelike separated. These points can neither affect, nor be affected, by each other. The three regions are separated by the "light cone", which consists of the points that you could send a lightray to (or from). I'm too lazy to draw a picture right now, but you can see a pretty good explanation here.
Next up, we'll talk about rotations. As always, readers are free to ask me questions in the comments box.
If interpreting the imaginary root requires flipping the sign and taking what would otherwise have been distance as duration instead, does that leave such a thing as true 'distance in spacetime'? Somehow I had gotten it into my head that I could meaningfully talk about 1990, e.g., as being located '23 light years away in spacetime'. I guess that's nonsense. But if so, spacetime seems to lack conceptual unity -- i.e., it's not really one object, because space is still space and time is still just duration, tacked onto the three spatial dimensions. Or is there something I'm not getting?
Mark,
Thanks for your question. But I'm having difficulty answering it because I'm not totally sure how to interpret some of your phrases (such as "true `distance in spacetime' ") and "conceptual unity/one object" in a mathematically precise way. Or worse, I can imagine different possible ways to interpet these phrases, and some of the ways make your statements true and other ways make it false. So instead I'll say a bunch of things that are true and hope it helps.
(Usually when you ask an expert what you think is a simple yes-no question, they hem and haw and eventually say "it depends". Part of becoming an expert is learning the language in which is easiest to formulate the right questions; that's why it's so hard to translate.)
1. Yes, the concept of "distance in space" and "duration in time" are different; the first applies to points which are spacelike separated and the second to points which are timelike separated. There exist ways to meaningfully distinguish between spacelike and timelike given our laws of physics (e.g. there are 3 space dimensions but only one time, some stuff travels slower than light (i.e. in timelike directions) but nothing we know about travels faster than light (i.e. in spacelike directions). In other words, there is no symmetry which flips the notions of distance and duration. (Although you might be able to cook up alternative laws of physics which have a space/time flipping symmetry, like a 1+1 dimensional world with only massless particles so everything moves at the speed of light.)
2. On the other hand, there is no absolute meaning to picking out one particular direction of time as special, or a 3D plane of 3 particular space directions as special. That's because there IS a symmetry which mixes up the time coordinates and space coordinates, the Lorentz boost. See The Ten Symmetries of Spacetime. However, this symmetry does not ever allow you to turn a spacelike direction into a timelike direction. It does allow you to do things like tilt a spacelike direction "timeward" so that it is angled a bit in the time direction, but not so much that it becomes timelike.
When we say that spacetime is unified, we mean (2) and not (1).
3. Is 1990 (on earth) 23 lightyears away? I think it's probably best to think of this as a pure convention. Distance is not duration. However, nothing stops us from using "natural units" where the speed of light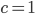
. This amounts to measuring time and space using the same units (say years = lightyears) and then it would be quite literally true that 1990 is 23 units away from us.
On the other hand, nothing stops us from being perverse and adopting units instead where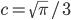
. The equations will look uglier, but all the physics will be the same. In that convention, if we keep lightyears as the unit, it's not going to be true that 1990 is 23 units away. It's just a question of how you choose to measure.
Hi Dear Aron :
So if as far as I understand the issue if signature of spacetime be Euclidean ( ++++) we can definitely and surely say there is no any possible notion of causality,time and change ,indeed 4D Euclidean pure space is necessarily and absolutely A-causal ( Causality-free) ,timeless and changeless , am I right ?
Cheers,
Kaveh
Yes Kaveh, that's more or less right. Although you could still describe a field as "changing" in the sense that its value depends on one of the spatial coordinates, say
. And, given enough "initial data" about the fields at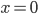 
, you can usually use the field equations to determine the values of the fields at any other value of 
.
In fact, the way field equations defined in Euclidean signature usually work, their solutions are usually analytic, meaning that you can reconstruct the field everywhere if you know the value of the field in any finite sized region, however small. That's quite different from what happens in Lorentzian signature (+++-), where you can modify the fields independently in different locations, and it can't affect you in any way until you wait long enough for a signal to arrive. This is the "causality" property of Lorentzian field theories.
Dear Aron :
Of course I dont think that even we can talk about change,changing in time is not equal to variation in space,so change of field with regard to spatial coordinates is not change at all. There is another point that even many experts couldn't or don't want to believe , if universe at the most fundamental ontological level is described by something such as no-boundary proposal of Hartle-Hawking or tunneling from nothing model of Vilenkin universe absolutely has neither a beginning point (beginning in the sense of geometric or thermodynamic) nor is beginningless ( cyclic/biuncing models,time-loop model and all past infinite models) but is timeless,causality-less ,changeless and spaceless and indeed is a mathematical structure.
beginninglessness indeed in both above mentioned theories universe is timeless,causality-less,changeless and spaceless mmmodel model
Hi Aron, I wonder if you check comments on old posts, and if so whether you'd mind giving brief answers to three questions on time please? I am a regular reader and I understand most of what you write, though with just two years of Physics at University I miss some of the "heavier" stuff.
1. A lot of people say time is measured by change, even defined by change. Would you say this is true, or is it defined mathematically?
2. Can time pass without change?
3. Is it theoretically possible that a universe could exist that has 3 spatial dimensions plus time, but no matter or energy (hence time passes without change), or would such a universe be a physical contradiction?
I hope you don't mind giving a brief answer please, when you have time. Thanks. Eric
Eric,
Yes, I do see comments on old posts. Some might say that your questions are really metaphysical questions. But according to the usual way of thinking about our current laws of physics, the answer is clear:
1. No, it is defined mathematically by the existence of a time dimension in the geometry (which may then be parameterized by a time coordinate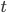
).
2. Yes, in almost every model of physics we have, there exist states where nothing changes with time. These are called "stationary" states, and actually you can prove that for any theory of physics constructed according to the usual rules, if there exists a "vacuum state" (one with the lowest possible energy) then it is necessarily stationary. ("Unstable" theories without a lowest possible energy are usually regarded as undesirable.) There may be other stationary states in addition, depending on the details of the theory.
It is not regarded as any more weird than a state that happens to be symmetric with respect to translating the
coordinate.
3. Yes, empty Minkowski spacetime, with no energy or matter in it, is a valid solution to the equations of both General Relativity and Quantum Field Theory. (The definition of "empty" is rather subtle in QFT due to the presence of quantum fluctuations in the fields which are always there even in the vaccum state; but the precise statement is that there exists a state of lowest energy, which is invariant under a time translation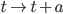
, as well as the other symmetries in the Poincare group.)
Hi Aron, thanks a lot. Yes, they are metaphysical questions, but it seems best to start with the physics. Thanks.
I get scared of natural units. If you wanted to find the geodesic a particle takes I think you'd integrate dS but if its natural units do you have to keep in dt? Im not sure on the details but cant you divide out dt so that you're integrating the inverse of the Lorentz factor (up to a sign convention). Then take a time integral of the Lagrangian?
Andrew,
The units don't really make a difference. It's just, if you don't use natural units, you have to include some factors of c in various places.
And yes, if you want to calculate the proper duration of a timelike geodesic segment in special relativity, you can indeed use the equality:
The first formula is better conceptually, since it's more obviously Lorentz invariant, but the second may make it easier to do the calculation.
I'm not sure why you talk about integrating ds to "find" the geodesic, while it is true that a timelike geodesic has the property of maximizing the value of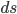
, it's much easier to just use the fact that it is a straight line.