There is a theorem due to Borde, Guth, and Vilenkin which might be taken as evidence for a beginning of time.
Roughly speaking, this theorem says that in any expanding cosmology, spacetime has to be incomplete to the past. In other words, the BGV theorem tells us that while there might be an "eternal inflation" scenario where inflation lasts forever to the future, inflation still has to have had some type of beginning in the past. BGV show that "nearly all" geodesics hit some type of beginning of the spacetime, although there may be some which can be extended infinitely far back to the past.
If we assume that the universe was always expanding, so that the BGV theorem applies, then presumably there must have been some type of initial singularity.
The fine-print (some readers may wish to skip this section):
[BGV do not need to assume that the universe is homogeneous (the same everywhere on average) or isotropic (the same in each direction on average). Although the universe does seem to be homogeneous and isotropic so far as we can tell, they don't use this assumption.
More precisely, let 
be the Hubble constant which says how rapidly the universe is expanding. In general this is not a fully coordinate-invariant notion, but BGV get around that by imagining a bunch of "comoving observers", one at each spatial position, and defining the Hubble constant by the rate at which these observers are expanding away from each other. The comoving observers are assumed to follow the path of geodesics, i.e. paths through spacetime which are as straight as possible, that is without any acceleration.
Now let us consider a different type of geodesic—the path taken by a lightray through spacetime. Now if the average value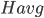 
along some lightlike geodesic is positive, then BGV prove that it must reach a boundary of the expanding region in a finite amount of time. In other words, these lightlike geodesics reach all the way back to some type of "beginning of time" (or at least the beginning of the expanding region of spacetime which we are considering).
We can also consider timelike geodesics, describing the motion of particles travelling at less than the speed of light. For nearly all timelike geodesics, if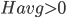 
then that geodesic also begins at a beginning of time. However, the theorem only applies to geodesics which are moving at a finite velocity with respect to the original geodesics which we used to define 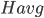. The original set of observers is allowed to extend back infinitely far back in time.
As an example of this, one can consider a spacetime metric of the following form:
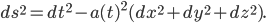
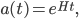
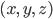. But nevertheless, observers travelling at a finite velocity relative to those hit a beginning of time (or else exit the region of spacetime where this metric is valid).
Since the BGV theorem only refers to the average value of the expansion, it applies even to cosmologies which cyclically oscillate between expanding and contracting phases, so long as there is more expansion (during the expanding phases) then there is contraction (during the contracting phases).
On the other hand, in certain cases even an expanding cosmology may have 0 average expansion, due to the fact that we are averaging over an infinite amount of time. So the BGV theorem does not rule out e.g. a universe where the scale factor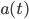 
approaches some constant value in the distant past.]
The fine print is now over.
All right, everyone who skipped the details section is back, yes?
The BGV theorem is sometimes referred to as a "singularity theorem", but it is not really very closely connected to the others, because it doesn't use an energy condition or any other substantive physical assumption. It's really just a mathematical statement that all possible expanding geometries have this property of not being complete.
Carroll correctly observes that the BGV theorem relies on spacetime being classical:
So I’d like to talk about the Borde-Guth-Vilenkin theorem since Dr. Craig emphasizes it. The rough translation is that in some universes, not all, the space-time description that we have as a classical space-time breaks down at some point in the past. Where Dr. Craig says that the Borde-Guth-Vilenkin theorem implies the universe had a beginning, that is false. That is not what it says. What it says is that our ability to describe the universe classically, that is to say, not including the effects of quantum mechanics, gives out. That may be because there’s a beginning or it may be because the universe is eternal, either because the assumptions of the theorem were violated or because quantum mechanics becomes important.
It is quite true that the BGV theorem is proven only for classical metrics, although I see no particular reason to believe that its conclusion (if the universe is always expanding, than it had an edge) breaks down for quantum spacetimes.
However, Carroll's secondary point that the assumptions of the theorem might not hold seems even more devastating. It says that there must be a beginning if the universe is always expanding. So maybe have it contract first, and then expand. That's an easy way around the BGV theorem, and (as Carroll points out) there are a number of models like that. On this point I agree with Carroll that the BGV theorem is not by itself particularly strong evidence for a beginning.
Aron:
Interesting stuff and thank you.
I have a few question.
1) Based on your understanding of all the cosmological model and the hypotheses floating around (including yours), what is the view of most physicists on the question of whether the universe has a beginning and whether the Big Bang is the beginning of time. It seems logical to conclude that if most physicists accept the Big Bang as the standard cosmological theory, then most (must?) accept the notion of a universe with a beginning. But I could be wrong.
2) In “Did the Universe Begin? II: Singularity Theorems” you mentioned "Generalized Second Law" “(GSL), which says that the Second Law of thermodynamics applies to black holes and similar types of horizons.” On the bouncing universe scenario, Stephen Barr writes in “Modern Physics and Ancient Faith”:
“The Second Law of Thermodynamics suggests that the “entropy”, or the amount of disorder, of the universe will be greater with each successive bounce……Given this, it would seem unlikely that the universe has already undergone an infinite number of bounces in the past.”
3) Is the thermodynamics argument of Barr about the bouncing scenario the same as your yours? That is, the universe could not have gone through an infinite number of “Big Crunches and “Big Bangs”, each bounce as fresh as the previous one, and still satisfy the physics of the Second Law of thermodynamics applies. So there is a contradiction.
I realise you’re a busy man and thanks for your time.
The Big Bang Model really refers to the history of the universe after the Big Bang. I would guess most cosmologists would say they don't know for sure whether there really was a beginning, that it sort of looks like there was, but that quantum gravity effects might resolve the singularity. But we don't really do science using opinion polls, so I don't really know. I'm trying to summarize the evidence the best I can.
I'll get to the argument from the Second Law of Thermodynamics in a later post. This is a separate argument from the Penrose Singularity Theorem. It turns out that you can recast both of these arguments in terms of the GSL, but even so they remain seperate arguments. If you apply my singularity theorem to an initial singularity such as the Big Bang, you actually have to use the time-reverse of the GSL, so it's not the same argument. Hopefully I'll be able to explain the distinctions when it comes up.
Aron:
Thank you for the response.
As a non-physicist, please explain in plain English how “quantum gravity effects might resolve the singularity.” I am assuming you mean that using Einstein’s equations (with no “quantum gravity effects”), at t=0 , the result is that both the density of matter and the curvature of space time become infinite. But with the quantum gravity effects, this initial singularity vanishes, so that we cannot speak of a beginning of the universe and therefore a t=0.
I would be keen to know about the plausibility of these alternative models that attempt to explain away a beginning ; what simplifying assumptions are used, and I am not suggesting that the motivation is anti-Biblical, though (from experience) I am not persuaded that personal beliefs and biases have no influence one goes about building a model.
If you would be taking up this topic in your upcoming Posts, I can wait.
A nit.. please fix the typo in the sentence "(or else exist the region of spacetime where this metric is valid)."
I think you 'exit' not exist'
Great blog.
-David
[Fixed. Thanks--AW]
TY,
As you say, Einstein's equations would predict that the curvature of spacetime goes to infinity as we approach the Big Bang. But we also know that if the curvature gets large enough (certainly once the distance scale of curvature is as tiny as the Planck scale) then the classical Einstein equation doesn't apply.
You could tell several different stories about the early universe which might go under the general heading "quantum gravity effects resolving the singularity". For example, it could be that once the curvatures get large enough, there is a "bounce" connecting our expanding universe to a prior contracting phase, which is also approximately classical. Or it could be that time reaches an end, but the curvatures don't go to infinity. Or it could be that once you go back early enough, there is a "region" of spacetime where ordinary classical concepts of spacetime break down and something else replaces them. This "something else" might or might not be eternal to the past (if the question even has a meaning once classical concept of time goes away....) All of this is just unpacking the plain English phrase "We don't know for sure what happens. (Although, in this series I am trying to discuss the limited evidence we have, such as it is.)
Aron,
I was wondering if you would be so kind as to offer a few points of clarification. Is it possible that you might be mistaken to write,
The reason I ask is, based on everything that I have read, it seems to me that the BGV theorem does not rely on spacetime being classical:
Vilenkin would later seem to state this point even more explicitly:
Unless I’m missing something, Vilenkin seems to unquestionably affirm the applicability of BGV to the quantum regime—if we include the relevant data for the quantum regime in our calculation of Hav and still find that Hav>0, then we would know that our spacetime (i.e., the combination of classical and quantum) is necessarily past-incomplete.
Moreover, this exact question came up in Dr. Craig’s debate with Prof. Lawrence Krauss. During his opening statement, Krauss produced a personal email from Vilenkin that read, “Note for example that the BGV theorem uses a classical picture of spacetime. In the regime where gravity becomes essentially quantum, we may not even know the right questions to ask.” Given the apparent conflict with his previous proclamations, Craig personally wrote (http://www.reasonablefaith.org/honesty-transparency-full-disclosure-and-bgv-theorem) to Vilenkin for clarification:
Vilenkin answered:
Nevertheless, I fully acknowledge my limitations regarding subject-matter expertise here and am well-aware of the possibility that I may have misunderstood something. If so, I would appreciate correction.
However, if I am correct in my interpretation of Vilenkin’s assessment of BGV, then it would seem to follow that the theorem is strong evidence for an absolute beginning: if classical spacetime reaches a boundary in the finite past due to Hav over its history equaling >0, then the only way to restore past completeness is to find some plausible mechanism for whatever is on the other side of that boundary to exist eternally in a state of Hav≤0; but my novitiate survey of the literature found no such mechanism. Even leaving aside any philosophical objections that might arise, there still does not seem to be any viable cosmogonic models that did not fail on scientific grounds.
In “emergent universe” scenarios, one of the extreme difficulties (in addition to the fatal philosophical problem of internal incoherence) is crafting a system that somehow either (1) oscillates “forever” or (2) remains static “forever,” and then proceeds to evolve into the expansion phase. As it was noted here (http://arxiv.org/abs/1306.3232):
Here (http://arxiv.org/abs/1204.4658)agrees: even if a mechanism could be found to facilitate the transition from the asymptotically static/periodic state, still, “there do not seem to any matter sources that admit solutions that are immune to collapse.” And one final affirmation (http://arxiv.org/abs/1110.4096):
Another seemingly possible way to evade BGV is via a cyclic model. However, as you touched on, BGV is applicable here provided we average the scale factor over each individual cycle. And if we were to do so, we would surely find Hav>0 due to the effects of entropy increase and accumulation in each successive cycle.
Finally, we come to models positing an infinite contraction. I would like to ask about the part where you say the following:
Sure, it would seem that a model that posits a prior contracting phase certainly evades BVG—the time coordinate τ will vary monotonically from −∞ to +∞ as spacetime contracts for all τ 0. But how does that entail that models of this sort are in fact viable options? In a personal communication with James Sinclair, George Ellis identifies two problems that plague these models:
But let’s leave all of that aside. As it turns out (if I understand correctly), the same incompleteness theorem that proved past incompleteness in a spacetime with H_av>0, will also prove future incompleteness (http://arxiv.org/abs/1403.1599) in a spacetime with H_av<0:
Isn’t it true that the reason BGV proves past incompleteness in a spacetime with Hav>0 correctly explained by the following: if we trace the worldline of a geodesic observer (timelike or null trajectory) as she moves through an expanding spacetime, we will find that the observer slows down relative to a congruence of comoving test particles. Thus, if we follow the observer backwards, we will see that she speeds up relative to the comoving test particles; and the calculation shows that she will reach the speed of light in a finite proper time. Therefore, the geodesic is incomplete to the past.
Consequently, would not the relative velocity between a congruence of comoving test particles and a geodesic observer moving through a contracting spacetime from t = −∞ be measured as increasing? If so, then won’t the observer reach the speed of light in a finite proper time (finite affine length, in the null case)? If she will, then doesn’t that show that she will never make it to the bouncing phase at t = 0? I think that it does, which would therefore entail that, necessarily, no such model positing an infinite contraction could ever make it to the bounce phase and subsequent expansion. Therefore, as it turns out, models of this sort don’t in fact escape BGV.
Jack,
You make some good comments about difficulties with many of the pre-Big Bang models. However, in the case of Aguirre-Gratton, the arrow of time reverses prior to the bounce. This makes Ellis' comments about the need to fine-tune the conditions at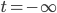
inapplicable, because the "initial conditions" are instead specified at 
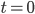, the moment of the bounce. Although this approach raises some philosophical issues of its own, which I plan to discuss later.
Regarding inconsistency with BGV, you write:
That paragraph seems correct to me, but I don't think the next one is right:
Yes, the relative velocity is increasing during the contacting phase, but starting from any specific time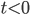
, there is only a finite amount of time before the bounce, so no conflict with the BGV theorem. The infinte length of time contacting in the past can't conflict with BGV any more than an infinite amount of time expanding to the future can do so.
If you consider the case of de Sitter space (which contracts and then expands), you can work out explicitly that there is no contradiction with BGV. (As you get farther and farther away from the bounce, the relative velocity to the comoving particles gets smaller and smaller, and thus you have more and more time before the BGV theorem causes trouble.)
Aron,
Thanks for taking the time to respond to my post. I am aware of the fact that the Aguirre-Gratton model evades BGV due to the highly speculative arrow of time reversal. Additionally I affirm that this model is but one of many that fail to satisfy the only condition assumed by BGV, and thus can be said to evade the theorem. But as I say, a model’s mere avoidance of the condition Hav > 0 is far from a demonstration of its plausibility. And in the AG model what we have is an approach that aims to simply transfer the problem of enforcing low-entropy boundary conditions to the bounce hypersurface, rather than at t=−∞. Far from resolving all the difficulties, this approach actually creates many more (which you touch on in your wonderful paper http://iopscience.iop.org/0264-9381/30/16/165003).
Let’s see if I can sufficiently articulate my contention that the BGV seems to render models positing an infinite contraction geodesically past (future?) incomplete. You’ll recall that I took a moment to briefly outline just how exactly BGV proves kinematic incompleteness for Hav > 0 spacetimes: given that the relative velocity between a geodesic observer and an expanding congruence of comoving test particles decreases over time, it follows that the velocity will increase as we rewind the time while tracing the observer's worldline to the past; and we reach the speed of light in a finite proper time.
With that in mind, my point is simply this: in an assessment of an expanding spacetime, the act of “rewind[ing] the time while tracing the observer's worldline to the past” produces conditions identical to what we find for t < 0 in infinitely-contracting spacetimes—namely, the relative motion between each member of a congruence of comoving test particles is of an approaching sort, unlike the recessionary motion found in expanding spacetimes. Now, you agree with me that “the relative velocity is increasing during the contacting phase.” But tell me this: if BGV proves that the observer will reach the speed of light in a finite proper time, then, given the infinite duration of time from t = -∞ to t = 0, shouldn't the observer reach the speed of light short of arriving at t = 0? How could she not? Not matter how long BGV says that proper time time will be, it is still finite. So an infinite amount of time would surely be sufficient for arriving at the speed of light.
You maintain that, “starting from any specific time t < 0, there is only a finite amount of time before the bounce, so no conflict with the BGV theorem.” I wholeheartedly agree—for any arbitrary point before t = 0 there is only a finite duration until the bounce is reached. But in order to have geodesic completeness, the wordline must necessarily extend all the way back to t = -∞, not just to some arbitrary point t < 0. Therefore, the observer will be measuring the relative velocity between herself and the contracting congruence of comoving test particles for an infinite amount of time. Therefore, given that BGV proves she will reach the speed of light in some finite amount of time, the infinite amount of time she spends in the contracting phase prior to t = 0 is sufficient to necessitate geodesic incompleteness.
Hi Aron,
Thank you for this post and your helpful discussion with Jack Spell. I have a question regarding the Aguirre model. In Alan Guth's paper "Eternal inflation and its implications" ( http://arxiv.org/pdf/hep-th/0702178.pdf?origin=publication_detail ), Guth discusses the Aguirre model and puts it in the category of not being reasonable or plausible. I assumed it was because the model required a reversal in the arrow of time. Can you discuss the Guth paper in this context and do you agree with Guth that the Aguirre model is not reasonable or plausible?
Welcome Ron,
I looked at the Guth paper and I didn't see where he calls the Aguirre-Gratton model not "reasonable" or "plasible". He says in the abstract that under reasonable assumptions, you can prove that inflation had a beginning. He also says on page 14 that under "plausible" assumptions, the universe is finite to the past (due to the BGV theorem). But I don't think that Guth is saying the Aguirre-Gratton model is unreasonable or implausible. "Plausible" just means reasonably likely, and I feel that ito say that some idea is plausible or reasonable, is a relatively weak statment, not nearly as strong as saying that the opposite idea is implausible or unreasonable. That's just how I parse the English terms, other people may feel differently about it. Apparently nowadays Guth thinks the universe probably didn't have a beginning (as mentioned by Carroll in the debate).
Anyway, I'll be giving my own opinion of Aguirre-Gratton and related models in future posts.
Jack writes:
The BGV theorem says that if the observer starts at particular time with a finite nonzero velocity relative to the comoving observers, and then waits a long enough time, she'll reach the speed of light in a finite amount of time. The smaller the initial velocity, the greater the time before there is a problem. But, in the limit that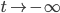
, her starting velocity also gets smaller and smaller. As you go towards 
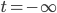, her starting velocity gets infinitesimally small, and the time needed before there is a conflict gets infinitely long. So there is no conflict with the BGV theorem.
If you do the calculation explicitly in the case of de Sitter space, you will see that what I am saying is true.
Aron,
Thanks again for finding the time to respond; I hope you are able to do so further when you return from France. Unfortunately, though, I'm sorry to say I still cannot agree that there is no conflict between BGV and spacetimes positing an infinite contraction. Although, I do want to be clear about something: I am well aware that all of this is a little above my pay grade; thus my disagreement is probably due to ignorance of some fundamental point on my part; so I would greatly appreciate any additional expertise that you might provide to help me gain a proper understanding.
Before engaging in another endeavor to articulate why I believe BGV to conflict with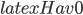
), BGV proves that there will be causal geodesics that, when extended to the past of an arbitrary point, reach the boundary of the inflating region of spacetime in a finite proper time $latex \tau$ (finite affine length, in the null case).
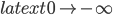is a quantity that is actually infinite (
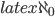) rather than potentially infinite (
).
The measure of temporal duration
If we agree on the veracity of those three statements, then I want us to keep them in mind as we turn to what was said in your last comment. I'll break it down into two parts:
The BGV theorem says that if the observer starts at particular time with a finite nonzero velocity relative to the comoving observers, and then waits a long enough time, she'll reach the speed of light in a finite amount of time. . . .
That seems to be in accord with what was implicit in (2): if the velocity of a geodesic observer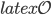
(relative to comoving observers in an expanding congruence) in an inertial reference frame is measured at an arbitrary time 
to be any finite nonzero value, then she will necessarily reach the speed of light at some time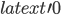 
is to be avoided), then the time coordinate 
will run monotonically from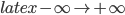 
as spacetime contracts during 
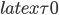. In other words, the limit would not be 
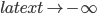because 
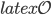wouldn't approach 
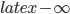; rather, it seems to me 
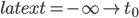would be the limit because 
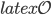would slowly approach 
.
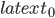Thus, if what I have argued above is correct (and it very well may not be), then the implications are unmistakable: as long as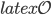
:
is a non-comoving geodesic observer;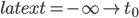
;
;
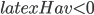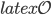will get faster and faster as she approaches the bounce at 
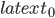. Moreover, since we know that will reach the speed of light in a finite proper time 
, coupled with the fact that the interval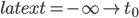 
is infinite, we can be sure the she will reach the speed of light well-before ever making it to the bounce—and therefore cannot be geodesically complete.
is in an inertial reference frame;
is moving from
is tracing a worldline through a contracting spacetime were
it therefore follows that the relative velocity of
Man, my formatting got all out of whack. Go here http://jackspellblog.wordpress.com/2014/06/17/extending-the-bgv-theorem-to-cosmogonic-models-positing-an-infinite-contraction/ to read it,
Jack,
Regarding your summary of the argument:
1. Correct
2. I would add, that BGV prove that this very geodesic is incomplete, assuming it is not comoving with the original set of geodesics used to define the expansion of the universe.
3. Normally physicists leave talk of "actual" vs. "potential" infinite to the philosophers; in any case I don't see how it is relevant to what BGV showed.
Regarding your continued argument that the BGV rules out AG, I think that in your last sentence there is the same problem as before. Let me make an analogy this time.
The following premises are all true: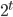
is finite and positive for every finite value of 
.
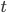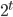doubles in time at each elapsed second (
).
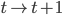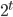is defined for arbitrarily negative times, 
.
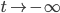I. If a finite positive quantity doubles in time every second, then it becomes greater than 10 in a finite time
II. The quantity
III. The quantity
IV. The function
However, the following argument based on these premises is not: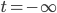
to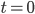 
is infinite, it follows that 
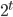will become greater than 10 some finite time after 
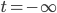. This proves that 
for values of 
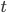well before 
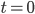, which is a contradiction. Therefore, the function 
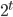is impossible.
V. Since the amount of time from
The mistake in the argument is a change in the order of limits. At any finite time, the amount of time needed is finite, but one cannot conclude that at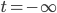
, the amount of time needed is finite, because 
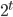is infinitesimal at 
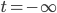. The situation with BGV is exactly like this.
Again I say, your extension of BGV cannot possibly be correct, because if it were correct, it would rule out de Sitter space, but de Sitter space is a perfectly consistent spacetime metric.
This is now my third comment making these same points. If you still do not agree, I suggest you go figure out how to actually do the calculation in the case of de Sitter space. You will see that there is no contradiction.
Aron,
I appreciate you taking the time necessary for your three comments. Still, I do not agree with them. But I do want to thank you, though, for your patience through all of my questioning. Though your last reply seems to indicate that this discussion has ceased to warrant your interest, I would still like to make this effort to provide clarification for several misunderstandings.
It’s unfortunate that you hastily dismissed my inquiry regarding infinites as irrelevant, when this seems to me to be not only relevant, but also at the very heart of this disagreement (as I shall try once more to show). In response to your points in the order they were stated:
1. Finally, something we agree on! :)
I guess I should’ve elaborated a bit. Perhaps if I had done so you would’ve known that the relevant talking in this case is that which is done by the mathematicians.
2. I’m fine with the addition.
3. I suppose that I am to blame for your dismissive attitude here
When I speak of a potential infinite, I am referring to the same thing
the lemniscate
that Cantor called the “variable finite” and denoted with the sign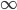 
. The role of this infinite is to serve as an ideal limit and it is most certainly the infinite that you continue to use in this discussion.
Contrast that with an actual infinite. This infinite, pronounced by Cantor to be the “true infinite,” is denoted by the symbol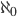
(aleph zero). This infinite represents the value that indicates the number of all the numbers in the series 1, 2, 3, . . . This is the infinite to which I continue to refer in this discussion.
Just to be clear, an actual infinite is a collection of definite, distinct objects, and whose size is the same as the set of natural numbers. A potential infinite contains a number of members whose membership is not definite, but can be increased without limit. Thus, a potential infinite is more appropriately described as indefinite. The most crucial distinction that I am attempting to convey is that an actual infinite is a collection comprising a determinate whole that actually possesses an infinite number of members; a potential infinite never actually attains an infinite number of members, but does perpetually increase.
With that distinction in mind, let’s talk about your analogy.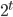
does not double in time at each elapsed second unless the value of 
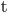is both finite and positive. What you’ve done by plugging in a negative value, far from doubling the quantity each second, actually causes the quantity to be cut in half each second. Mathematically, this premise formulated as such helps shed light on the task of distinguishing a potential infinite from an actual infinite. Namely, while you can continue indefinitely to divide each successive quantity in half, the series of subintervals generated consequently is merely potentially infinite, in that infinity serves as a limit that one endlessly approaches but can never reach. Time, in much the same way as space, is infinitely divisible only in the sense that the divisions can proceed indefinitely, but time is never actually infinitely divided, in exactly the same way that one simply cannot arrive at a single point in space.
I. No dispute here.
II. Again, looks good.
III. Despite what was asserted prior to the first premise, this premise is clearly false: the quantity
I.V. Okay.
V. Even though I believe this analogy to be a very poor likeness of my position, I am optimistic that it can actually be used to show where our misunderstanding lies. In order to construe the analogy properly so that it parallels contracting spacetimes, let’s take a closer look at each premise:
I. We don’t need to do anything to change this premise because it beautifully mirrors the implications of BGV: namely, the part where the relative velocities increase successively, and then the observer reaches the speed of light in a finite time.
from your thought; just forget about them for a moment. Now, the analogy requires that the value be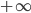 
rather than 
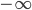for the premises to all to be true. Thus, I would consequently reason as follows:
II. While this premise is true, I’ve already pointed out that if the time is to double each second then the value chosen must be positive. So let’s add in that property.
III. If we make the necessary change called for in (II), then this premise will be correct.
IV. Again, in order to mimic the relative velocities of the Observer and test particles the value chosen must be positive. Otherwise the velocity does not successively increase.
V. And finally, in order to best understand my contention, you must evacuate the notion of limits and
1. If a finite positive quantity doubles every second, then it becomes greater than 10 in a finite duration of time.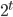
is a finite positive quantity that doubles every second if and only if 
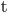is positive.
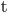is positive.
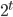is a finite positive quantity that doubles every second. (MP, 2,3)
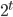becomes greater than 10 in a finite duration of time. (MP, 1,4)
2.
3.
4. Therefore,
5. Therefore,
Having concluded the truth of (5), ask yourself, if the proposition,
6. A finite duration of time has elapsed.
is also true, then how does the conclusion,
7.
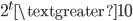
not follow necessarily?
That is the crux of this whole thing, and it has nothing to do with the order of limits. It is simply my perception that, if there were an infinite contraction phase, it therefore follows that there has elapsed an actually infinite duration of time. And if an infinite amount of time is not enough for our Observer to hit lightspeed, nothing is. In any case, what do you understand the following to mean:
As far as de Sitter space goes, my contention wouldn’t rule out dS as a viable metric; it would rule it out as a viable eternal metric. You seem to think that it is eternal, but how do you understand:
and on p.18 here (http://online.kitp.ucsb.edu/online/strings_c03/guth/pdf/KITPGuth_2up.pdf)?
Jack,
As you gathered I don't really have the energy to continue this discussion much further, but here are three parting comments:
1. When I said that the function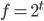
doubles every second, I mean that 
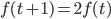. This is true even for negative values of 
.
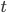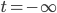, it's finite for any finite 
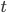), bounces, and then expands again.
2. If the question really comes down to actual vs. potential infinities, why couldn't the proponent of an infinite past just say that it's a potential infinity rather than an actual one?
3. The flat slicing of de Sitter is only a patch of the complete de Sitter space. The complete de Sitter space is described by a geometry where space at one time is a sphere, and it contracts down from infinite size (at
I guess, Aron, it seems to me that the entire issue comes down to the concept of "necessary and sufficient conditions." I would simply ask, Is an actualized infinite amount of time sufficient to necessitate arriving at light speed? If yes, then why is my argument incorrect? If no, then you've basically just undermined and disagreed with the crux of BGV.
Actually, let me rephrase my dilemma:
1. If an actually infinite amount of time is sufficient to reach light speed, then why isn't light speed reached and therefore my argument correct?
2. If an actually infinite amount of time is not sufficient to reach light speed, then what is sufficient to reach it?
Jack,
Starting from any finite nonzero speed, it takes a finite amount of time to reach light speed. The smaller the initial speed, the longer it takes to reach light speed.
Starting from an infinitesimal speed, it takes an infinite amount of time to reach light speed.
The latter is the situation in Aguirre-Grattan and related models. That's all.
Since you insist on using the distinction between actual and potential infinities, I will insist that the infinite past of AG is a potential rather than an actual infinity. That is, there is not a real time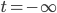
, there are only times with arbitrarily large negative values of 
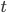. When I say that the speed is infinitesimal at 
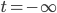, I really mean that 
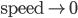as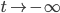 
.
Aron,
You stated:
That's fine. But the point is that the temporal duration prior to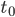
is an infinite amount of time. Thus, even starting at an infinitesimal speed (and therefore requiring an infinite amount of time to reach light speed), light speed will be reached because we would in fact have an infinite temporal interval elapse prior to 
.
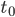As far as your comment that "I will insist that the infinite past of AG is a potential rather than an actual infinity" goes, I have to respectfully say that it seems that you have misunderstood the difference between the two infinites. As I said, the potential infinite is never actualized (i.e., achieved) while the actual infinite is realized. In order for us to have traversed the necessary infinite temporal interval of an infinite contraction, that infinite cannot be merely potential; it must be actual because we would have already traversed it.
Please disregard my last paragraph--I overlooked the part where you where specifying that the AG model is potential. I agree with you completely. I thought you were saying all infinitely contracting models are potential. Sorry.
No, that just doesn't follow. You have to be VERY CAREFUL when making arguments like that about infinity, because there are lots of things that can go wrong. You've probably heard about those paradoxes about things like infinity over infinity. It could be one, but it could also be any other number. You can't just reason about infinity as if it were a finite number; mathematically there are any number of examples where it doesn't work out. Talking about "infinitesimals" is sloppy anyway, and I'm sorry if that confused you. A mathematician would tell you that you should instead formulate all the infintesimal and infinite quantities being considered here as limits of finite quantities.
I've already said more than enough times why it doesn't work in this particular case. The correct conclusion in the case of AG, is that there exists some time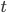
, such that a) there is an infinite amount of time before 
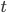, and b) if the universe cannot be contracting on average until 
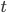. It does not follow that for any time 
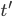, if (a) then (b). These statements are no longer the same statement when the amounts of time involved are infinite.
As I said before, you can see this quite explicitly by thinking about simple examples like the function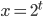
, for which it is true that 
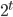exceeds any given value of 
at some sufficiently large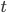 
, and yet false that it exceeds any given value of 
at any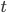 
. (Even though there is an infinite amount of time between 
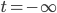and any finite 
).
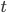This is my absolute last reply on this subject; if you still disagree you can either reread what I've already written or else go to somebody you trust more.
I realize that you said that the previous reply will be your absolute last on this subject, but I’ve asked you twice now for your take on a passage where I believe Vilenkin is in agreement with me. This will be the third time I am asking you to share your thoughts on the following:
If he is not arguing exactly what I have been, what is he arguing?
From the context of his paper, I don't think he was talking about the AG model (in which there is an expanding region in which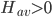
), but rather a model with infinitely many AdS bounces, for which 
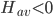throughout the whole spacetime history. He can't possibly have meant that BGV rules out AG, since it doesn't. But if you're still unsure, you can ask him about it.
Obviously I am a pushover who can't enforce my own statements about not arguing anymore. Well, this time for real! :-)
LOL. Yeah, you are a pushover :). Seriously, though, I appreciate all of your time. I have emailed Dr. Vilenkin for clarification and hope that he can find the time to respond.
On a side note, I was not necessarily arguing against the AG Model because it can be interpreted at least two different ways (not to mention one's own theory of time can come into play to further complicate things). Nevertheless, thanks again for all of your thoughts.
You're welcome!
Oops---I responded to this thread again! Look what you made me do! :-)
Aron,
Thanks for this helpful post. My friends and I so appreciate what young cosmologists like you and Luke Barnes ("Letters to Nature") are doing to bring clarity and objectivity to these complicated scientific issues.
After reading your post above, one thing puzzles me. Why, if the BGV theorem is ultimately agnostic on whether the universe is past eternal, did Vilenkin make such a strong statement to the contrary in his book, Many Worlds in One? He writes:
"It is said that an argument is what convinces reasonable men and a proof is what it takes to convince even an unreasonable man. With the proof now in place, cosmologists can no longer hide behind the possibility of a past-eternal universe. There is no escape, they have to face the problem of a cosmic beginning." (p. 176).
Vilenkin toed a similar line when he attended Steven Hawking's 70th birthday party in 2012. New Scientist had an article covering the event under the title, "Death of the Eternal Cosmos," referring not to the future heat death of the universe but rather to the death of the IDEA that the cosmos can be past eternal. It quoted Vilenkin as saying, "All the evidence says the universe had a beginning."
In light of what you've written above, Vilenkin's statement in Many Worlds in One seems quite over the top, and his statement at Hawking's birthday celebration would have to be toned down to the rather tame, "This PHASE of our universe had a beginning."
I don't know if you've ever had a chance to ask him about these things, but I thought perhaps you have since in one of his 2013 papers he mentions you at the end as someone who gave a helpful critique.
Hi Wallace,
I'm not Aron (obviously!) but I wanted to note that Vilenkin has also mentioned through personal correspondence with Bill Craig that there are always caveats and assumptions with any given theorem (http://www.reasonablefaith.org/honesty-transparency-full-disclosure-and-bgv-theorem):
...
I also think Aron's post above didn't claim that the BGV theorem is agnostic on whether the universe had a beginning, so much as that it's inconclusive on its own. The theorem does seem to imply a beginning, but it perhaps requires support for its assumptions (or support demonstrating that a violation of its assumptions leads to problems).
Hi Aron. I noticed on the wiki page of Horava Lifshitz gravity that " the speed of light has an infinite value at high energies.".http://en.wikipedia.org/wiki/Hořava–Lifshitz_gravity
It seems that if this is the case, this would also violate the idea that the BGV proves a beginning. Would you agree?
Dr. Wall,
I'm having trouble understanding whether or not there is any evidence for there being a quantum regime prior to the classical space-time boundary. It seems to me there is no direct evidence for this, so my question is, can there be any empirical evidence for such a regime, or must this ultimately end up being a mathematical exercise that produces a consistent philosophical conclusion?
John-Michael,
It is true that there's no direct evidence for a quantum regime. Our confidence in one comes mainly from two directions.
First, classical general relativity tells us that space-time curvature is determined by mass-energy content in a non-linear way (you could say that gravity itself gravitates). As a consequence, increasing mass-energy densities lead to "runaway" curvature increases that produce singularities and at very high energies the theory itself breaks down... space-time comes to an end. Now there's no reason why the universe cannot produce such singularities, but this may also mean that the theory simply isn't valid any longer and must be replaced. Second, quantum complementarity tells us that precision in time (and therefore space via ct) implies large fluctuations in energy that at a small enough scale are large enough to disrupt the very structure of space-time itself.
Thus, we have two separate well-verified physical frameworks that independently lead us to the conclusion that at short enough distances and high enough energy densities the relativistic and quantum worlds seem to unite and become indistinguishable from each other. Either they unite, or they need to be replaced by something else. Unfortunately, to unpack all of this we must be able to observe distance and energy scales that can only be probed by constructing a large hadron collider the diameter of the solar system and operating it for an extended period. Needless to say, that is not going to happen any time soon.
But that said, there is some indirect evidence that may be within our reach. Inflationary scenarios predict broad power spectrum density fluctuations in the cosmic microwave background (CMB) due to quantum fluctuations in the inflaton potential. These density fluctuations have been observed and they fit the predictions almost perfectly. Those with the longest wavelengths (the lowest multipole harmonics) correspond to the earliest fluctuations with the largest energies. Since inflation is thought to have begun at, or very shortly after the Planck era, these low multipole fluctuations may have been close enough to it to give us a peek at the quantum realm. The catch is that the dynamics of inflation and the energies involved are closely tied to the nature of the inflaton itself... about which we still know next to nothing. Furthermore, while inflation is perhaps the strongest contender for explaining these fluctuations (among other things) it isn't the only one, and as such has yet to be definitively proven. There is another possibility here in that inflation also predicts that these quantum fluctuations will produce small-scale gravity waves that may be detectable as "B-mode" polarizations in the CMB. If found they would truly be a "smoking gun" for inflation. Last spring's BICEP2 results did find B-mode polarizations in the CMB that were initially thought to be due to these gravity waves, and as such caused a great deal of excitement. Unfortunately they turned out to be spurious (a story for another day). But if these primordial inflationary gravity waves ever are discovered, and/or an inflaton is discovered that renders the dynamics of inflation precise, we may well have confirmation of the existence of the quantum regime. Of course, we would still have a long way to go to explore that regime properly.
So to sum up... while there is no direct evidence of the quantum regime, we have very good theoretical reasons for it, and some indirect observational evidence as well. I hope that helps!
As always Aron, if I missed on anything feel free to correct me. :-)
would the B mode really have been a smoking gun for inflation? Perhaps not :
http://arxiv.org/abs/1106.5059
Howie, actually the smoking gun is broad-spectrum gravity waves. I mentioned B-mode polarization in the CMB only because that is one very good way to detect them, assuming of course that noise corrections are good enough. However as you, and this paper note, there are other things that might produce them as well, not the least of which is interstellar dust... which of course, is what happened to the BICEP2 results last year. Other options for gravity wave detection are in the works though--ones that do not have the problematic noise sources that plague B-mode polarized CMB searches by platforms like the BICEP series of experiments. The main point I was making was simply that while there is no direct evidence of a quantum realm, we do have a few windows for perhaps confirming one indirectly... even if we cannot explore it in detail any time soon. Of these, the most notable is probably LIGO (the Laser Interferometry Gravity-wave Observatory). Once the Advanced LIGO platform is fully online (middle of this year) another round of observations will begin... and this time we may get lucky! (Interestingly, my thesis adviser is now director of the LIGO Hanford project!) Best.
Wallace,
I haven't just talked with Alex, I've co-authored a paper with him! (arXiv:1312.3956) But I don't want to put myself forward as the world-expert in what he thinks. I'll just register my own opinion that those particular quotations seem to be overstated, although as St. Robert points out he's put things more moderately elsewhere.
I like the quote about how "a proof is what it takes to convince even an unreasonable man", but I would add that a sufficiently unreasonable man would not be persuaded even by that. Perhaps more relevantly, many important things in life do not admit of proof, and therefore it is not surprising that there are always lots of unreasonable people to disagree with in these areas of life...
John,
Once the curvature/density of the universe is high enough, classical physics breaks down and quantum gravity effects are almost bound to be important. The only way this could be avoided is if something else we don't understand kicks in before that point. So either way, something we don't understand was important in the very early universe!
howie,
That's an excellent question!
(For those not in the loop, Horava-Lifshitz gravity is a speculative quantum gravity model in which, unlike general relativity, there is a preferred rest frame everywhere. There are a number of problems with this approach, but one positive is that it seems to solve the "nonrenormalizability" problem of quantum gravity.)
My first instinct was to say that since the BGV theorem uses relativity in the proof, obviously it won't apply to Horava gravity. My second thought was to try to see if the proof could be modified to extend to this case. But eventually I realized that the answer is quite subtle and interesting...
In GR, the basic concept is that of the metric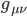
, which is a field that tells us the lengths and times and angles of curves passing through any given point. The concepts of "geodesic" and "proper time" are derived concepts, defined by using the metric. The BGV theorem uses these concepts, since it says that in a universe which contains a family of "geodesics" which are "expanding" away from each other, any "geodesic" which is comoving relative to the original family extends backwards for only a finite amount of "proper time". I've put scarequotes around each concept which is defined using the metric.
Now like GR, Horava gravity has a metric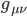
, but it also has some additional structure. The additional structure is a foliation, i.e. a way of slicing spacetime into 3 dimensional surfaces representing space at one time. So at any given point we can define concepts using either the metric or the foliation, or else both. (We can also use the foliation to define alternative metrics besides the one we started with, using what's called a "field redefinition").
Now the BGV theorem is a purely geometrical statement which applies to any metric whatsoever, regardless of where it came from. This means that, if we take any metric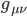
defined in Horava gravity, and define a "geodesic" G and its "proper length" with respect to that particular metric, the BGV theorem will still apply to G, framed in those terms. But there may well be OTHER concepts of "time", defined using the foliation, according to which that same curve G has experienced an infinite amount of time.
Recall that in relativity, things experience less time when they are moving close to the speed of light. But in Horava gravity we can define alternative "clocks" which don't have this property (basically, by defining time at each point in the preferred rest frame at that point.) And according to these types of clocks, these curves may experience an infinite amount of time.
So I think this means it's a little bit ambiguous whether BGV holds or not. It depends on which "curves" you want to think about, and what "clock" you want to measure them with. GR is kind of special because it gives us one particularly natural choice of curves (geodesics) and clocks (proper time).
Given this ambiguity, the real question is which concepts are the most important from a physical point of view, i.e. to ask which concepts are the most useful for various purposes. Ideally these would be somehow associated with the physical behavior of actual matter in Horava gravity. It's not obvious to me what should play the role of a "geodesic" in Horava gravity. It would be interesting to calculate the dynamics of a wave pulse in Horava gravity to see approximately what path it follows. (Of course real matter doesn't exactly follow geodesics in either GR or Horava gravity, since waves spread out and there are often other forces acting...)
My instinct is to think that if a curve has infinite length as measured by any reasonable (locally defined) clock, then it probably isn't physically meaningful to talk about extending it any further than that. So tentatively I would suggest that at least the "spirit" of the BGV result is likely to be violated, but (as you can see from my response) this is not an entirely straightforward question, and it depends to a large extent on how you choose to define things.
Pingback: Did the Universe Have a Beginning? – Carroll vs Craig Review (Part 1) | Letters to Nature
Hello Aron,
I’m sorry to say that I’ve been away from your blog for quite a few months now. After looking over the old posts I regret that I’ve missed so much. I’ve recently been enjoying spending some time posting at W L Craig’s Reasonable Faith forum page. (If you’d like to see some interesting discussion—including my own input—on apologetic topics like religious experience, the Canaanite genocide, why there isn’t overwhelming evidence for Christianity or theism, or Daniel’s prophecy of the 70 weeks, I’ll give you some links.)
I’ve recently been looking at some of Craig’s debates and dialogues with scientists and have run into one question I hope you would be willing to help me with. Since the above topic you discussed in 2014 looked to me to be the closest I could find to my question, I thought I would add it on to this discussion.
From Vilenkin’s email to Krauss which Krause used to debate with Craig:
“Of course there is no such thing as absolute certainty in science, especially in matters like the creation of the universe. Note for example that the BGV theorem uses a classical picture of spacetime. In the regime where gravity becomes essentially quantum, we may not even know the right questions to ask.”
From Vilenkin’s email to Craig after Craig asked for further explanation (Sept 2013):
“The question of whether or not the universe had a beginning assumes a classical spacetime, in which the notions of time and causality can be defined. On very small time and length scales, quantum fluctuations in the structure of spacetime could be so large that these classical concepts become totally inapplicable. Then we do not really have a language to describe what is happening, because all our physics concepts are deeply rooted in the concepts of space and time. This is what I mean when I say that we do not even know what the right questions are.”
Is Vilenkin saying that even assuming an on average expanding universe, we could possibly have a beginningless universe given the quantum fluctuations? Or is he using these possible unknowns afforded by quantum fluctuations as only a means by which a workable, beginningless cyclic model might be allowed? (I’m aware there are other problems with cyclic models which must also be overcome.)
It’s good to get back in contact with you again, Aron.
Dennis
Hi... I don't have a physics education so this is mostly foreign language to me.
Could you explain in more common terms what is wrong with the idea that in time as we know it, cause always comes before effect, and this couldn't have happened an infinite number of times before now or we would not have reached the present...so therefore time must have a first moment, itself being dependent on (or a quality of) something timeless (in a manner different from temperal cause and effect)?
Thanks :)
Annie,
If time goes infinitely far to the past, then there was no first moment. (Just like, if time goes infinitely to the future, there will be no last moment). There are just moments of time which are arbitrarily early.
I think your argument that "this couldn't have happened an infinite number of times before now or we would not have reached the present" presupposes that "we" had to begin at the begining of time and keep going through it until we arrived, like a train going along the railway tracks. But since there was no first moment of time, there is no "we" or any other physical object that actually has to traverse an infinite time.
So maybe cause and effect don't work like that, and all of time simply exists together, like this:
... -3 -> -2 -> -1 -> 0 -> 1 -> 2 -> 3 ...
where each moment (labelled by a number) is the cause of the next moment. If that is impossible, it can't be a simple mathematical inconsistency since the past part of the timeline looks just like the future part, only flipped around backwards. You would have to argue that it is somehow hidden in meaning of the concept "cause" that it cannot go back forever, even though effects might go forwards forever. That would be more of a philosophical argument than a physics one.
There was some additional discussion of this issue in the comments to the post Open and Closed.
Hello Annie,
In physics one speaks of interactions rather than causes & effects. The numbers in Aron's timeline are all said to "co-exist" in some interrelated way. Now many natural processes interact in ways that favor one direction on that timeline. China breaks when we drop it for instance, but we don't observe broken cups and plates suddenly reassembling themselves and jumping into our hands even though the equations of physics allow that. This includes the ways our five senses interact with the world around us as well. Since these processes seem to prefer one direction of the number line they define an arrow of time, and this asymmetrical arrow is what allows us to distinguish one side of an interaction as the "cause" and the other as its "effect" (or past from future). In the absence of such an arrow, none of the numbers in Aron's diagram would occupy any preferred place relative to the others, and the arrows between them could point in either direction or be replaced by dashes. Physicists and philosophers refer to this as the B-Theory of time.
Arguments against an infinite past usually don't involve notions of cause and effect per se (or at least, the best ones don't). They argue instead that the existence of physical infinities (as opposed to mathematical ones) leads to absurdities. The best know example of this is Hilbert's Hotel. These are philosophical arguments and are not strictly based on physics.
There's another theory of time though, in which an argument like the one you've described might be made, and it's known as (surprise, surprise) the A-Theory. According to the A-Theory, only the present moment exists--the past is gone and the future is coming into existence continually. This would be like reading Aron's number line from left to right with your finger, and only the number you were touching at any point would actually exist. A-Theories can be made to work within the framework of our current physics, and philosophers like William Lane Craig have argued for them. However from the standpoint of relativity and quantum mechanics they're messy, and most physicists will tell you they create more problems than they solve. Aron has excellent discussions of these issues here and here.
Hope this helps too! :-)
" According to the A-Theory, only the present moment exists"
Is this a meaningful statement? Or an abuse of the word "exist"?
Simply put, it is the things that can be said to exist--some things are existing at the present moment, other things existed in the past moments (and not now) and yet other things will exist in the future moments.
But to speak of "moments existing" I submit is simply incoherent. The moments do not exist in the same way the things do. Things exist in moments but moments are not something that can be said to exist.
Hello professor wall, I love your blog. I have a questions about BGV theorem. In this blog you said that a way to avoid the theorem as Carroll suggests is to have the universe contract first then expand. Is there anything wrong with the contracting models of the universe that would prevent our universe from contracting in a way to avoid the BGV theorem? I read that models that contract and expand needs a special boundary condition for the bounce to happen. And most models don't offer any mechanism for it. Thank you for your time billy
Pingback: Did the universe have a beginning? - Ozzblog
Pingback: Did the universe have a beginning? Did it arise from nothing?
Hello Prof. Wall, thank you so much for this blog. It's really help me understand a lot about the current discussion when it comes to the "beginning" of the universe. I just had three questions that I was wondering if you could explain or clarify to me. The first is: I was watching "Closer to Truth" yesterday and Dr. Sean Carroll said that we can't trust classical spacetime because it "points to a singularity or points towards infinity" and then he said we can't trust it because it "doesn't mix with quantum mechanics". Is that true, in the way that cosmologists don't trust it anymore because it points to a singularity? What exactly does he mean, and does that therefore invalidate it's explanatory power when referring to the Big Bang? My second question is referring to what he said in his blog post recently about the BGV theorem. He said "The BGV theorem says that, under some assumptions spacetime had a singularity in the past. But it only refers to classical spacetime, so says nothing definitive about the real world". What does he mean by that? And if that's true, does that mean it's inadequate to critique other cosmological models if it only refers to classical spacetime which he already says is not true? Because Dr. Craig uses the BGV theorem in a lot of his lectures to say that the variety of cosmological models all end up having a beginning according to the BGV theorem. Is he mistaken by doing this because that theorem assumes an "invalid" view of the "classical spacetime"? What do you think about the explanatory power of the BGV theorem? And lastly: You're a physicist and a Christian, what are your views on the "beginning" of our universe based on the evidence from cosmology apart from the opening chapters of the Bible? Because there are constantly new theories being created for how the universe could be finite or eternal, do those eternal models seem probable? You're in a sense, one of the few people who can truly understand the advanced technical language of what's truly being said/assumed here by their models, so what do you think is most probable based on the evidence, and how does that effect your faith?
I understand you're probably extremely busy, but I thank you again for your blog. It's been very helpful to me and my walk in searching for Truth.
"On this point I agree with Carroll that the BGV theorem is not by itself particularly strong evidence for a beginning"
Father Spitzer of the Magis Center claims that the BGV theorem proves that the Universe had a beginning. He is in contradiction with Aquinas, who tells us that we cannot prove whether or not the universe had a beginning. I find Aquinas to be a rather amazing thinker, and I knew that in The Summa he answered the question: "Whether It Is an Article of Faith that the World Began" (Ia Q46 A2).
"Objection 4" seems to be metaphorically equivalent to Spitzer's claim that BVG proves the world had a beginning and the "Reply to Objection 4" is metaphorically equivalent to your comment here.
The rest of Aquinas' article is similarly very interesting.
Have you, a reader of the Great Books, read it?
Tom Cohoe. Father Spitzer has never claimed the BVG PROVES the beginning of the universe; only that it supplies excellent additional EVIDENCE for the beginning. You are falling into the falsehood that Aron Wall keeps repeating, is the claim that Craig (Spitzer?) states that "If the BVG is correct, then the universe has a beginning", which is logically equivalent to "If the universe does not have a beginning, then the BVG is wrong". This is complete nonsense the BVG can be true without a beginning - it may only describe the, on average, expanding part of the universe. The point that Spitzer, Craig make is that these models that evade the beginning are mathematical toys, mathematically incoherent, do not describe a space time at all and are even to be regarded as useful computational devices. Carroll does not understand the BVG very well as he consistently claims that the BVG only applies to 'classical spacetimes' those describable by General Relativity - this is completely wrong.
David McKinnon. See here https://www.reasonablefaith.org/writings/question-answer/honesty-transparency-full-disclosure-and-the-borde-guth-vilenkin-theorem/ . Personally I do not think that Aron Wall understands the BVG very well himself. Carroll certainly does not.
Mark Strange,
I would agree with most of what you've said regarding the BGV theorem. I would add a couple of caveats though...
First, I trust he'll correct me if I'm mistaken, but I don't believe Aron has ever said that Craig thinks it proves the universe had a beginning. What he's saying is that in his opinion the theorem isn't as strong an argument for one as Craig thinks it is. As long as there are models like Aguirre-Gratton (and a similar one of Carroll's) that manage to evade it, then however contrived they might be (so far at least), tying arguments for the creation of the universe to it carries some risks. That erodes its evidentiary usefulness to some extent, and he's more worried about that than Craig is.
Second, AFAIK, neither Aron nor Carroll ever said that BGV only applies to general-relativistic spacetimes. What they've said is that the theorem has only been proven for spacetimes that are "classical" in the sense of being pseudo-riemannian--that is, globally differentiable with non-degenerate metrics and geodesics--and also have a well-defined arrow of time. Essentially, that amounts to saying that it's only been proven rigorously for non-quantum spacetimes. That covers a lot more than just general relativity alone.
Aron did say earlier that his "first instinct" was to think BGV was based on GR, but he went on to discuss how the theorem is purely geometrical and applies to any metric whatsoever, regardless of where it came from. In fact, he also stated above that so far at least, like Vilenkin, he sees no reason to assume that BGV breaks down even for quantum spacetimes, and then discussed how it might be applied to one such case, Horava Lifshitz gravity.
---------------------------------------
Tom Cohoe,
I'm not familiar with Father Spitzer or the Magis Center, but even if the BGV theorem did definitively prove that the universe had a beginning that wouldn't contradict Aquinas. His argument was based on Aristotelian metaphysics--specifically, that a cosmological argument can't be based on accidentally-ordered causality alone. That has little to do with physics per se, and needless to say, was formulated long before modern cosmology opened the door to arguments based on theory and observation.
Craig promotes a Neo Lorentzian view of relativity which denies the speed of light is the maximum speed limit of the universe . But The BGV assume the speed of light is the maximum speed limit. So it seems the two are incompatible, so doesn't Craig have to chose which one to let go?
Scott Church,
The "accidents" of "reply to objection 4" are not different than accidents of particular laws of physics proposed as the true laws of the material substrate of the universe. The argument still applies unless you make the additional metaphysical assumption that what is going on is what is modeled in physics but there can be no proof for that - it is just an assumption. The RO4 argument is correct because it argues that there cannot be a proof of the finite absolute history of the world, and the metaphysical assumption obviates proof.
The argument is not a proof about the universe. It is a proof that there is no proof about the universe. The universe could bounce eternally with violations of the assumed laws of physics near the bounce times. It would have zero average expansion and BVG would not apply.
Mark Strange,
Spitzer's enthusiasm for BVG is so overstated that I should be forgiven for saying that he claimed to have a proof. He said "for virtually every conceivable pre big bang universal condition that we can conceive of going back as far as you want you're going to have to have a boundary of past time and eventually you're going to have a boundary which is absolute, a boundary which is a beginning of [garbled word] time itself." Take out the word "virtually" and it looks like a claim of proof to me.
Anyway, I do not see that the differential equations of general relativity exclude solutions in which the universe bounces forever.
howie,
St. Craig is a bit notorious for making arguments based on assumptions which his listeners believe, even if he does not personally share those assumptions.
I don't think being a Neo Lorentzian necessarily requires denying that the speed of light is the maximum speed. It does require breaking Lorentz Invariance though, and in a way which might problematize the interpretation of the BGV theorem (see my earlier answer to you), although not its actual validity as a mathematical theorem since that only requires the existence of an expanding Lorentzian metric.
Hello Dr.Wall,
I hope you are doing well and staying healthy. My name is Bill Gambone and I have been reading your work on your blog and I hope you can help me with a question I have. My question is on a statement Sean Carroll made about the BGV theorem. He states “So maybe have it contract first, and then expand. That's an easy way around the BGV theorem, and (as Carroll points out) there are a number of models like that”
But I always thought it must be on average expanding for BGV to work? Even if it bounces then expands more on average then would BGV still apply? Thank you for your time sincerely Bill
Billy,
Yes, the BGV theorem can be proven even if it only is expanding on average. Presumbaly Carroll was thinking of cases in which this condition does not hold.