In this post, I've put some more technical details about what the concept of imaginary time means, to help clarify the previous post about the Hartle-Hawking No Boundary Proposal. If you don't want to have to understand equations, skip this.
First of all, a bit of remedial math. There are a lot of functions which (even if they teach them to you in school as being functions of real numbers) actually make sense when extended to complex numbers of the form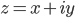 
. I already had to say something about complex numbers earlier in this series. If you know how to add, subtract, multiply, and divide complex numbers, you can pretty easily make sense out of polynomial fractions like 
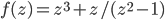, but you can also make sense out of things like sines and cosines and exponentials. For example, if we take an exponential of an imaginary number we get
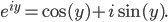
So when you see something in a scientific equation like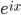 
, that looks like an exponential, but the power is imaginary, that's really something that's spinning around in the complex plane as you change 
, without growing or shrinking in its absolute size. It is a general rule that things which oscillate in the real direction correspond to things which exponentially grow and/or shrink in the imaginary direction, and vice versa.
This process of extending functions to the complex plane is called analytic continuation, and functions which can be so continued are called (wait for it!) analytic. (Not all functions are analytic: those which suffer from abrupt changes, like the absolute value function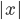 
, are not. 
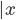changes unpredictably at 
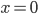; if someone told you what it looks like for 
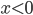, and you tried to extrapolate it to 
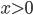you'd guess wrong.
Now it turns out that there is a close mathematical connection between quantum mechanics and thermodynamics (a.k.a. statistical mechanics). Quantum mechanics is all about how the phase of a wavefunction oscillates around as time passes. The rate at which the phase spins around is proportional to the energy 
of the state, as told to us by Schrödinger's equation:
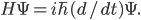
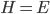spins around as time passes like 
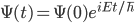, where 
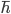is Planck's constant.
On the other hand, statistical mechanics is all about thermal equilibrium states, and the rule of thermal equilibrium is that the probability to be in a given state falls off exponentially with the energy. The probability is proportional to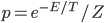 
, where 
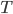is the temperature, and 
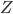is an extra random thing called the "partition function'' you throw in to normalize the probabilities so they add up to 1. It turns out that states like these maximize the entropy given how much entropy they have. If you squint these two exponentials they start looking quite similar to each other, if only you can accept the mystical truth that inverse temperature is like imaginary time:
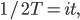
If you start with an initial condition where all states have equal probability, and "evolve'" for a finite quantity of "imaginary'" time, you end up with a thermal state ( after normalizing the total probabilities to be 1 at the end). Better still, if you start with (almost any) state and evolve for an infinite amount of imaginary time, you end up with the "vacuum" state of lowest energy, all other states being exponentially damped by comparison to that one.
Well, this may seem like a bit of mumbo-jumbo, but with the help of that complex number math I mentioned above, you can actually put it on a fairly rigorous footing, for ordinary QM systems, and even for quantum field theories. So of course, Hartle and Hawking had to be more bold than that, and try to apply this idea in the context of quantum gravity.
In quantum gravity (to the extent that we understand it), the dynamics are not governed by an ordinary Hamiltonian. Instead they are governed by a Hamiltonian constraint:
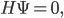
Now the Hartle-Hawking prescription is really just a clever way to calculate one particular state which (at the level of formally manipulating equations that we can't really make sense of) solves the Wheeler-DeWitt equation.
It tells us the wavefunction of the universe, expressing the "quantum amplitude" for any possible metric of space at one time to exist. (The quantum amplitude is just a term for the complex number saying what the wavefunction is for a particular possibility to occur. Take the absolute value squared and you get the probability.) Since there are many ways to slice spacetime into moments of time, all of them have to exist side-by-side in this wavefunction, late moments in time no less than early ones. That's what it means to solve the Wheeler-DeWitt equation!
It's not the only solution to the Wheeler-DeWitt equation, but it's an especially nice one. In some ways it is like a "vacuum" state of the theory, one especially nice state to which others may be compared. (In other ways, it's more like a thermal state, due to the fact that there is only a finite amount of imaginary time evolution, before one reaches the end of imaginary time).
In order to calculate the Hartle-Hawking amplitude that a given geometry for 3 dimensional space (call it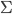 
) will appear ex nihilo (as it were), all you have to do is this:
1. Consider the space of all 4 dimensional curved spatial geometries whose only boundary is ,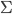
2. For each geometry, integrate the total value of the Ricci scalar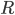 
over the 4 dimensional geometry, call that the action 
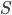, and assign to that geometry the value 
.
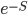3. Figure out how to integrate 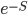over the infinite dimensional space of all possible 4 dimensional geometries. This requires choosing a measure on this space of possibilities, which is quite tricky for infinite dimensional spaces,
4. Cleverly dispose of several different kinds of infinities which pop up, and
5. Consider all possible choices of 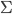and figure out how to normalize it so that the total probability adds to 1 (nobody knows how to do this properly either).
Good luck!
Aron,
I guess a book titled “Did the Universe Begin” is becoming long overdue.
As I have followed your ideas and explanations in these 9 epic blogs (and with more on the way) on this very theme, I am starting to feel that there are good scientific reasons to believe that the universe had a beginning in time, which requires God as the explanation (not a gap filler).
In a Brief History of Time, Hawking argues that the no boundary proposal does away with a Creator because a universe with no boundary or edge, a universe that is self-contained, has no beginning or end. But how robust is this conclusion drawn from so insecure (or unreal?) a notion as imaginary time (in the mathematical sense of complex numbers). We have also seen other sleight-of-hand attempts by cosmologist like Lawrence Krauss to remove God from creation in arguing spontaneous creation out of “quantum vacuum”. And you have refuted that rather succinctly in previous blogs.
I am with those who theists who believe that God is required regardless of whether there is a beginning. Since God is omnipotent what prevent Him from creating a universe with an infinite past? I don't think this generalisation does away with the Kalam argument favoured by St Craig and similar arguments (thermodynamic beginning). Conversely, in Bayesian langauge, they increase the prior probability of the role of a Creator.
Interesting it reminds me of a kind of imaginary time mentioned in my holy book . meaning that :
when the Hour arrives the guilty ones will be deluded thinking they remained dead but for an HOUR but to those to whom knowledge and faith is given they will say : You remained dead until the Creator His decree but you used not to know .
This means that when people will die there will be no passage of time perhaps but stil the soul wil perceive of some kind of time in the case of the wicked ones they will be deluded .
Peace
Dear Abdul,
Thanks for your comment. I should say that my post concerns time which is "imaginary" in the technical mathematical sense of a square root of a negative number, which is unrelated to the meaning of "imaginary" in the sense of delusional or nonexistant.
Nevertheless, you raise an interesting theological question about what is the state of people in between death and the General Resurrection of all human beings at the Final Judgement. From the scientific viewpoint we know that time (as we know it) is part of the physical universe, so if we talk about something outside of the physical universe it is not clear to what extent our temporal concepts still apply to the situation.
Christians believe that the souls of the righteous dead are alive to God, that they are in Christ and therefore live with him. The challenge is to relate these promises to the doctrine that God will raise everyone from the dead physically at the end of this age of history.
Conversely, there is one place in the New Testament which suggests the wicked may be punished immediately following death, but this is in the context of a parable---one of the many fictional story told by Jesus to illustrate a point---and there are very few details given.
The bulk of the New Testament teaching about the afterlife (even in the context of most of the passages cited above) concerns the more important issue of what happens during and after the Resurrection from the dead. There is only a tiny amount about the time in between. Correct me if I am wrong, but I believe the same is true in the Qur'an.
Peace to you too,
Aron
Thank you Aaron for your reply .
The only necessity in which I believe is the Creator . Stephen Hawking said because there is a Law called gravity there is no need for God . I would argue if there was no physical world as we know it there would be no need for gravity lol.
I am aware of the use of imaginary numbers however it seems that some people use this mathematical concept to negate any beginning of the physical word .
Therefor I referred to the verse in quran in its literal sense .(being deluded)
whenever one dies he enters the Barzakh according to Islam .
Linguistically, “Barzakh” means a veil, barrier or partition between two things. So in context of resurrection it is the state between death and resurrection .
They ask you, [O Muhammad], about the Hour: when is its arrival? Say, "Its knowledge is only with my Lord. None will reveal its time except Him. It lays heavily upon the heavens and the earth. It will not come upon you except unexpectedly." They ask you as if you are familiar with it. Say, "Its knowledge is only with Allah , but most of the people do not know."
Allah also says in chapter 40 verse 57:
The creation of the heavens and the earth is definitely a greater thing
than creation of mankind, however, most of mankind knows not. Qur'an 40:57
Qur'an Chapter 33 Verse 63
Men ask you of the Hour, Say the knowledge of it is with God only,
What can convey to you that may be the Hour is near.
Qur'an Chapter 29 Verse 53
They bid you to hasten on the doom.
And if a term had not been appointed, the doom would have definitely come on them.
And it will come upon them suddenly when they perceive not.
Qur'an Chapter 53 Verse 57-59
The threatened hour is near. None beside God can disclose it. Are you surprised then at this statement?
So will it happen soon or over a long period of time? Only God knows , to us it is important to have prepared ourselves before entering that state , because as soon as one enters the Barzakh one's test of life test is over being at a believer or disbeliever .
So whoever follows Jesus son of Mary(puh) should keep follow the commandments and never ascribe partners unto God or to associate Him with creation .
from scientific perspective however it is difficult to prove resurrection directly . No man has been resurrected but resurrection from Islamic perspective is compared to clouds being lead to dead land and reviving the earth and there you have life .
Another view is from Allah His words .
Does man not consider that We created him from a [mere] sperm-drop - then at once he is a clear adversary?
And he presents for Us an example and forgets his [own] creation. He says, "Who will give life to bones while they are disintegrated?"
Say, "He will give them life who produced them the first time; and He is, of all creation, Knowing."
[It is] He who made for you from the green tree, fire, and then from it you ignite.
Is not He Who created the heavens and the earth able to create the like of them? Yea! and He is the Creator (of all), the Knower.
I hope this answers your question . peace be with you Aaron .
Hi Dr Wall, in the discussion of the Hartle-Hawking Model in Dr Craig's book "Reasonable Faith", I find two main points that I would request for your comments:
(1) "By positing a finite (imaginary) time on a closed surface prior to the Planck time rather than an infinite time on an open surface, such models actually seem to support, rather than undercut, the fact that time and the universe had a beginning."
Dr Craig says "Having a beginning does not entail having a beginning point... Time begins to exist just in case for any finite temporal interval, there are only a finite number of equal temporal intervals earlier than it.", So, in this sense, he seems to be saying that even "fuzzing into existence" is also some sort of a beginning.
He cites Dr John Barrow [Theories of Everything]: "This type of quantum universe has not always existed; it comes into being just as the classical cosmologies could, but it does not start at a Big Bang where physical quantities are infinite."
In this sense, he seems to believe that the Hartle-Hawking Model actually still makes a case for a beginning. Thoughts?
(2) "Introducing imaginary numbers for the time variable in Einstein’s equation has the peculiar effect of making the time dimension indistinguishable from space. But in that case, the imaginary time regime prior to the Planck time is not a spacetime at all, but a Euclidean four-dimensional space. Construed realistically, such a four-space would be evacuated of all temporal becoming and would simply exist timelessly..."
I think this is similar to what you discuss about "Euclidian (or "Riemannian") signature metrics" in your entry "Did the Universe Begin? VIII: The No Boundary Proposal", so then Dr Craig says:
(2a) "The question which arises for this construal of the model is whether such an imaginary time regime should be interpreted realistically or instrumentally. On this score, there can be little doubt that the use of imaginary quantities for time is a mere mathematical device without ontological significance. For, first, there is no intelligible physical interpretation of imaginary time on offer..."
Similarly, you also said in the same entry "This is because the Hartle-Hawking idea involves performing a "trick" [Wick Rotation], which is often done in mathematical physics, although in this case the physical meaning is not entirely clear."
(2b) "...time is metaphysically distinct from space, its moments being ordered by an earlier than relation which does not similarly order points in space. But this essential difference is obscured by imaginary time. Thus, “imaginary time” is most plausibly construed as a mathematical contrivance [!] Barrow observes, physicists have often carried out this “change time into space” procedure as a useful trick for doing certain problems in ordinary quantum mechanics, although they did not imagine that time was really like space. At the end of the calculation, they just swop back into the usual interpretation of there being one dimension of time and three dimensions of space." (Theories of Everything)
You also said something that parallels this: "However, there are some rather hand-waving arguments that the most probable Euclidean spacetime looks like a uniform spherical geometry. The spherical geometry is approximately classical, but there are also quantum fluctuations around it. When you convert it back to real time, a sphere looks like de Sitter space: hence the Hartle-Hawking state predicts that the universe should look have an initial condition that looks roughly like de Sitter space, plus some quantum fluctuations."
Dr Craig cites Dr Hawking (Brief History of Time): “Only if we could picture the universe in terms of imaginary time would there be no singularities... When one goes back to the real time in which we live, however, there will still appear to be singularities.”
He also cites Dr Vilenkin (Many Worlds in One) that the use of imaginary time as a mere “computational convenience” without ontological significance.
So agrees Dr Hawking, in other contexts, Dr Craig claims: "The clearest example of Hawking’s instrumentalism is his description in The Nature of Space and Time of particle pair creation in terms of an electron’s quantum tunneling in Euclidean space (with time being imaginary) and an electron/positron pair’s accelerating away from each other in Minkowski spacetime. This description is directly analogous to the Hartle-Hawking cosmological model; and yet no one would construe particle pair creation as literally the result of an electron's transitioning out of a timelessly existing four-space into our classical spacetime."
Do you agree with these statements?
Other Related Comments:
(3) In "Did the Universe Begin? VIII: The No Boundary Proposal" you said
"The Hartle-Hawking approach involves writing down what's called a functional integral over the space of all possible metrics for the imaginary-time geometry. There are an infinite-dimensional space of these metrics, and in this case nobody knows how to make sense of it...So Hartle and Hawking do what's called formal calculations, which is when you take a bunch of equations that don't really make sense, manipulate them algebraically as if they did make sense, cross your fingers and hope for the best."
Is this similar to Dr Feynman's sum-over-histories/sum-over-paths?
This all reminds me of another philosopher, Dr Tim Maudlin's remarks that:
"You have others saying that time is just an illusion, that there isn’t really a direction of time, and so forth. I myself think that all of the reasons that lead people to say things like that have very little merit, and that people have just been misled, largely by mistaking the mathematics they use to describe reality for reality itself. If you think that mathematical objects are not in time, and mathematical objects don’t change — which is perfectly true — and then you’re always using mathematical objects to describe the world, you could easily fall into the idea that the world itself doesn’t change, because your representations of it don’t."
Is this a fair assessment of what's happening in making models?
(4) On Arrow of Time Reversals: Dr Craig says in one of his recent podcasts “I think that is metaphysically absurd. Entropy increase is not to be identified with the direction of time. It is merely a physical measure of time. But time is a metaphysical reality that can exist quite independently of any clocks or physical measures of it...So at the very most, the direction of entropy increase can serve as a measure of time but it is not time itself.”
It isn't clear to me though how these categories (time and entropy) are assumed correlated/analogous or how entropy is a “physical measure of time” and also Dr Craig does not discuss why "at the neck of the hourglass" there is a reversal of entropy conditions and thus the arrow of time reversal.
(5) On deSitter spacetime: I think Dr Carroll alludes to his own model in a recent interview as his "favorite" the "empty space" model; he is referring to a deSitter space that births our universe, right? Is a dS spacetime really eternal in the past both geometrically and thermodynamically, when you said "this is an eternal spacetime which contracts down to a minimum size and then expands..."?
I saw two different illustrations of the Carroll-Chen model online in which (a) there is only one time arrowhead from the “negative” region of the dS “mother universe” through the bottleneck and into the “future” expansion and another showing (b) two different arrow heads mirror each other from the bottleneck with each having its own low to high entropy. Dr Craig calls scenario (a) “non-reductionistic” arrow of time and (b) “reductionistic” arrow of time. What do those mean? Does that distinction make sense in physics?
He comments “In these so-called “time-reverse models” what you’ve really got going on, I think, is a universe in which entropy is decreasing from eternity past for infinite time until it gets to this neck in the hourglass and then entropy begins to increase on the other side of that. That is thermodynamically impossible. It contradicts the second law of thermodynamics…”
Are there nuances here that Dr Craig may not be aware of?
Reply when you can. Thanks doc!
Raschid,
(1) There's a sense in which the Hartle-Hawking state has a beginning, and a sense in which it doesn't. We just need to be clear about the terminology. But as I said earlier in this series, despite Hawking's remarks seemingly to the contrary in popular literature, the Hartle-Hawking state does not in fact seem to have a beginning, when viewed from the perspective of real time.
(2) Yes, most physicists most of the time regard "imaginary time" as just a computational trick which isn't part of the real interpetation of physics. For example, when calculating the creation of electron and positron pairs in an electric field, or when calculating qunatum mechanical tunneling through barriers, the formalism is very useful, but everything could in principle be understood in terms of real time. So generally I'm inclined to agree.
But with the caveat that maybe if imaginary time really did play a fundamental role in the simplest description of our universe, this might be construed as evidence that we should take imaginary time more seriously as a physical concept.
(3) Yes, the "functional integral"/"path integral" is the same thing as Feynman's sum over histories, which is one of the definitions of quantum field theory. Since a "history" involves specifying the values of all the fields at each spacetime point, this involves something like an integral over an infinite dimensional space, which is tricky to define, but it makes sense in some cases.
I agree that mathematical models are not the same as the reality which they model. But I still think that relativity + theology + metaphysical arguments raise serious difficulties with a model in which only one time slice "really exists" at any time, for the reasons I began to discuss in parts I and II of my incomplete series on God and time. (Note the vicious circularity implicit in saying that "only one time exists at any time". Unless we interpret it as a tautology, or invent a new "meta-time" in which regular time can flow, this seems to be a circular definition...)
(4) St. Craig is assuming that the arrow of time we know about through "cause and effect" has nothing to do with entropy increase, but this is not an obvious assumption at all. Our ordinary experiences with cause and effect all involve situations where entropy is increasing. Entropy decrease would violate the normal statement of the Second Law of Thermodynamics, but the question is whether the Second Law is really a fundamental law of nature at all, or only a consequence of the particular initial conditions of our universe.
(5) Empty de Sitter space has no arrow of time at all. It is completely static and in fact has just as many symmetries as Minkowski spacetime.
There is a sense in which de Sitter space has 0 entropy (if you take the whole of de Sitter space) and another sense in which it has a positive entropy (if you restrict to the patch which can be seen by a single "observer", and attribute entropy and a temperature to the horizon beyond which the observer can't see anything). In neither case is the entropy of de Sitter space changing with time.
However, the story changes a bit if you postulate that the de Sitter space is actually unstable, and decays into "bubbles" of some other type of cosmology. If there is a particular time slice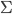
at which we stipulate there are no bubbles, then as we go either to the future or the past, bubbles may begin to form. In such a cosmology there are two thermodynamic arrows of time, pointing away from 
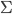in either time direcion.
I don't think that "reductionistic" vs. "nonreductionistic" is at all clear or helpful terminology. That's why I instead refer to "geometric" vs. "thermodynamic" beginnings.
I've been reading some of craig's callender work. He seems to suggest that time in quantum mechanics is essentially the same in newtonian mechanics, which would make it incompatible with the relativistic/minkowskian view of time. How are these to be reconciled? Well, it seems we have to wait to the unification of both. But, he suggests, that the implications of certain semiclassical results(such as the wheeler-de witt equation) which imply that there is no physical parameter "t" at all, would still aplly to QG. What are your views on that?
Flavio,
Well, you can certainly have both Minkowski spacetime and QM: it's called quantum field theory. As for the Hamiltonian constraint and what it implies about time, I discussed it here.
Hey Aron and or Scott,
Would like to see you guys interact with Sean Carroll's latest article trying to address why there is something rather than nothing.
https://arxiv.org/abs/1802.02231
Thanks
Hello Christopher,
As of this writing, I've only had a chance to skim this paper, but so far, I see nothing in it that wasn't addressed in my post on the "god hypothesis and its comment thread. In addition to the larger topic, I also addressed a number of claims Carroll has made elsewhere (e.g. - his book The Big Picture) and reiterates here. Another one of his favorite arguments turns up here as well--the so-called quantum eternity theorem used during his debate with William Lane Craig. Aron has dealt with the quantum eternity theorem at length here. For more on the topic of something-from-nothing, see Luke Barnes' posts Of Nothing and More Sweet Nothings at Letters from Nature, Ed Feser's post Carroll on laws and causation, or any of the sources I cited.
In my post, I mentioned metaphysically illiterate Atheist physicists who think they can explain away 2500 years of Western philosophy simply by redefining the word "nothing" and making magic a sub-discipline of physics. Unlike some of the more notorious such offenders, I certainly wouldn't call Carroll metaphysically illiterate. But ultimately, this paper is just one more example of that. In one sense at least, this only makes it worse. One might forgive people like Lawrence Krauss for their universe-from-nothing arguments because they truly are metaphysically illiterate and can't be expected to know any better. But it's strange that someone like Carroll doesn't--he minored in philosophy as an undergraduate and as noted, is known for his thoughtfulness and attention to metaphysical topics. There is, however, a well-known belief among many physicists that their recondite profession gives them a uniquely privileged access to Truth (note the capital "T") above and beyond all other human endeavors--a phenomenon often referred to as physics envy. Much as I admire Carroll for his contributions to physics, and his willingness to address metaphysical topics so many of his colleagues flippantly dismiss, he does seem to have a particularly bad case of it.
Best.