My own suspicion is that the Universe is not only queerer than we suppose, but queerer than we can suppose. – J.B.S. Haldane (Possible Worlds and Other Papers, 1927)
I was born hopelessly curious and under the tutelage of a nurturing teacher and parents who surrounded me with books, I fell in love with physics in the 2nd grade—when all my friends were enthralled with Batman, jets, and G.I. Joe. What drew me to it was the wonder of mysteries I couldn’t wrap my budding mind around, and chief among these was the notion that space, and time could be curved. I remember pouring over my parent’s Time-Life encyclopedia set which among other things, contained a full-color plate titled “Three kinds of space” featuring gridded surfaces shaped like a sphere, a pancake, and a saddle labeled +1, 0, and -1 respectively (the Friedmann constants, although of course, I didn’t know that then). I remember gazing at them struggling to understand… How can length, breadth, height, and duration be bent…? What does that even mean…? The question became even more mind-numbing when I later discovered that there can be spaces with more than three or four dimensions—indeed, an infinite number of dimensions—and these can all be curved as well. It wasn’t until well into graduate school that I started to get a shaky footing in that recondite landscape.
As three-dimensional beings, most of us grasp curvature visually. We can see curved lines and sheets against the backdrop of three dimensions because they bend into the other dimension/s. But how can three-dimensional space (or more properly four-dimensional space-time) bend when there are no other dimensions to bend into? The key to understanding this is to approach the question not by trying to visualize higher-dimensional spaces, but by exploring them with a mathematically based thought experiment physicists and mathematicians refer to as parallel transport. Let’s introduce two explorers: Flat Freddy who lives in a two-dimensional flat universe, and his sister Curved Cathy who lives in a curved one. For them, there is no third dimension much less any higher ones.
Parallel Transport
Let’s start with Freddy, placing him at the vertex of a triangle with two parallel vectors oriented along his direction of travel, one red and one green (Figure 1).
Figure 1
Now, let him go for a walk around the triangle’s perimeter in the direction the vectors are pointing, leaving the green vector behind, and taking the red one with him while ensuring that for the entire journey it remains oriented in the same direction (as we will soon see, this matters). Completing the first leg of the journey, he arrives at point B (Figure 2) with his red vector still parallel to the green one, and unchanged from its original orientation (light red).
Figure 2
Then, let’s have him journey an equal distance to the right at a 90-degree angle. When he arrives at point C, his red vector is still parallel to the green one and its previous orientations (Figure 3).
Figure 3
Finally, let’s take Freddy back home and reunite his two vectors. When Freddy checks his compass, he sees that point A is to his left and back at a 45-degree angle to the BC leg he just covered. When he arrives home again, he finds that his red and green triangles are still parallel to each other, exactly as they were when he began, and remained throughout his trek (Figure 4).
Figure 4
Getting his map out, Freddy sees that his journey traversed a right triangle with two 45-degree angles, the final leg of which covered a distance given by the Pythagorean Theorem,
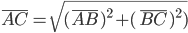 [Eqn. 1]
[Eqn. 1]
And enclosed an area given by,
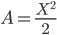 [Eqn. 2]
[Eqn. 2]
Where 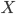 is the length of
is the length of 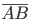 (or
(or 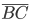 ). No surprises here. This is exactly what earth-bound three-dimensional creatures like us would expect.
). No surprises here. This is exactly what earth-bound three-dimensional creatures like us would expect.
Parallel Transport in Curved Space
Now, let’s have Cathy take the same journey in her universe. For clarity’s sake, let’s assume her universe is spherical with a “radius” that will better illustrate the outcome (more on why that word is in quotes soon). Like Freddy, we’re going to have her walk a triangular path beginning at point A with parallel red and green vectors, both tangent to the straightest path from point A to point B (Figure 5). As before, she will leave the green vector behind while carrying the red one with her, keeping it oriented in the same direction throughout. This time however, things are going to be a little more subtle. In Freddy’s universe the meaning of “straight” is clear enough. But as we will soon see, in Cathy’s this term will require a more precise definition.
Figure 5
When she completes the first leg of her journey at point B, her red vector hasn’t changed orientation. It is still pointing straight ahead, tangent to her path of travel (Figure 6).
Figure 6
Following in Freddy’s footsteps, she then journeys an equal distance to the right at a 90-degree angle, arriving at point C with her red vector still unchanged in direction (Figure 7).
Figure 7
Cathy has now travelled the same route from point A to point C that Freddy did in his universe and covered the same distance getting there. But now, something is amiss. When she checks her compass, she finds that point A isn’t to the left of her BC leg and 45 degrees back. Home is now 90 degrees to her left. Even more strangely, upon arriving home (Figure 8) she sees that her red vector is no longer parallel to the green one as it was when she started (light red). Now it is oriented at 90 degrees to it, even though it remained pointed in the same direction for the entire trip!
Figure 8
Furthermore, when she gets her map out, she sees that unlike her brother, she has traversed an equilateral triangle whose inner angles add up to 270 degrees rather than 180 degrees. And even though the final leg of her journey was noticeably shorter than Freddy’s, she traversed a larger region. Having studied higher mathematics at Flatland University, she is familiar with higher-dimensional spaces than the two dimensional one she knows, and an equilateral triangle with three 90-degree interior angles sounds suspiciously like a higher-dimensional sphere. Sure enough, when she measures the area enclosed by her journey, she finds that it is given by,
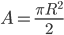 [Eqn. 3]
[Eqn. 3]
Where 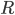 is a parameter that behaves mathematically like the radius of a three-dimensional sphere even though in her universe, there is no third dimension to contain one.
is a parameter that behaves mathematically like the radius of a three-dimensional sphere even though in her universe, there is no third dimension to contain one.
Note that Cathy’s conclusions were based only on measurements of distance and area, and the orientation of a vector she carried with her around a closed two-dimensional path. At no time did she step “outside” of her space into a third dimension from which the radius of a 3-D sphere could be observed. What she measured is simply a parameter that behaves like one in area calculations. Of course, Figures 5-8 are shown in 3-D perspective for heuristic purposes, but beyond that, there is no need for Cathy to postulate any higher dimensions to explain what she sees. As far as she knows, in her universe only two dimensions exist. How could Cathy’s two-dimensional universe be “spherical” when the sphere of our experience is a three-dimensional shape?
Straight vs. Geodesic
To answer this question, let’s go back to the turn of the 3rd Century B.C. when the Greek Mathematician Euclid published his Elements. In it, he laid the foundation of geometry in our three-dimensional space and Freddy’s two-dimensional one with five axioms, or postulates. Of these, four are interdependent in that each one can be formally derived from the remaining three. The remaining one, his fifth postulate, he stated as follows,
If a line segment intersects two straight lines forming two interior angles on the same side that are less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles. – (Heath, 1956)
It follows from this that if the two interior angles formed are equal to two right angles, those lines will never meet. Though Euclid doesn’t specifically say so, this would make the two lines parallel, which led 19th Century Scottish mathematician John Playfair to restate it in what today is perhaps its most popular version,
There is at most one line that can be drawn parallel to another given one through an external point.
For centuries, the fifth postulate troubled mathematicians because reasonable as it may seem, it’s entirely ad hoc. It has no interdependence with the other four and is superfluous to a complete formalism of Euclidean geometry. It was only a matter of time until people began to wonder what geometric doors would be opened if it were discarded.
The first step in that direction is a reexamination what we mean by straight and parallel. Like Freddy, most of us think of a line as straight if it is one-dimensional in the sense of having no curvature—or more formally perhaps, if all points on it share a common tangent vector in one direction. Likewise, we think of two lines as parallel if they lie within a common two-dimensional plane and are aligned in the same direction with no intersection point. Indeed, this is how mathematicians defined both terms for many centuries, and to this day Euclid’s fifth postulate is often referred to as his parallel postulate. But if it proves to be superfluous to the formalism of Euclidean geometry then non-Euclidean geometry becomes possible and these definitions will need to be revisited.
Without the fifth postulate, on an N-dimensional manifold (or space), a curve connecting any two points 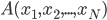 and
and 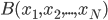 is said to be straight if, and only if it is the shortest distance between them on the manifold. In a flat space like Freddy’s (or ours), this reduces to our intuitive definition above, but that definition alone does not constrain manifolds to be flat. This suggests that if we want to quantify how paths between events are traversed in universes like Cathy’s, our mathematical descriptions need to be revised, and our parallel transport thought experiment gives us a clue as to how.
is said to be straight if, and only if it is the shortest distance between them on the manifold. In a flat space like Freddy’s (or ours), this reduces to our intuitive definition above, but that definition alone does not constrain manifolds to be flat. This suggests that if we want to quantify how paths between events are traversed in universes like Cathy’s, our mathematical descriptions need to be revised, and our parallel transport thought experiment gives us a clue as to how.
Modeling Curved Geometry
A full mathematical treatment of general relativity is beyond our scope today, but we can get our feet wet with an overview of the tools it will require. To model any N-dimensional space, be it flat or curved, there are two fundamental requirements we must meet.
First, we need a way to describe not only distances, but angles. To do that we will need to define at least two vectors at every point on it, 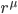 and
and 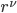 , where the indices
, where the indices 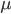 and
and 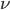 denote the N coordinates of each. Strictly speaking, they can be specified in any coordinate system of our choosing, and oriented in any non-parallel direction we like, but ideally, we want them to be orthogonal to each other (as shown in Figure 9) so that they define a coordinate system/s themselves. With these, we can then use a vector inner product, or dot product of them to define a matrix function
denote the N coordinates of each. Strictly speaking, they can be specified in any coordinate system of our choosing, and oriented in any non-parallel direction we like, but ideally, we want them to be orthogonal to each other (as shown in Figure 9) so that they define a coordinate system/s themselves. With these, we can then use a vector inner product, or dot product of them to define a matrix function 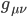 whose squared diagonal terms can be summed to give the squared distance along any interval, and whose off-diagonal terms are the dot product projections of each vector’s components onto those of the other. This function, which is referred to as the metric tensor,1 contains within its
whose squared diagonal terms can be summed to give the squared distance along any interval, and whose off-diagonal terms are the dot product projections of each vector’s components onto those of the other. This function, which is referred to as the metric tensor,1 contains within its 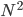 components a description of all lengths and trigonometric relationships between the two vectors.2 [Aron discusses this at length in his 2012 post All points look the same.]
components a description of all lengths and trigonometric relationships between the two vectors.2 [Aron discusses this at length in his 2012 post All points look the same.]
Figure 9
Neglecting time for simplicity (we’ll get to this later), in a flat 2-D space like Freddy’s, the two vectors will not have components that lie along each other so the off-diagonal terms will be zero, and the vectors are chosen so that their lengths define units in our chosen coordinate system,3 the diagonal terms will be 1 and the sum of their squares defines the Pythagorean theorem. Thus,
[Eqn. 4]
Second, we need to ensure that our models preserve one of the most sacred principles in physics—namely, that the universe exists independent of us, so its behavior should be independent of how we choose to describe it. If the most fundamental laws of physics are different here and now in this coordinate system and units than it is there and then in those coordinates and units, that would imply that we have an unreasonably unique status in it. In our hearts, we know that isn’t the case, so our descriptions of it should look the same in all frames of reference and units. In physics this is referred to as the principle of general covariance.
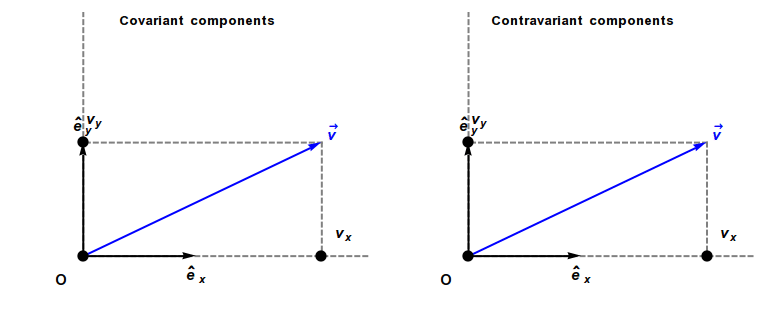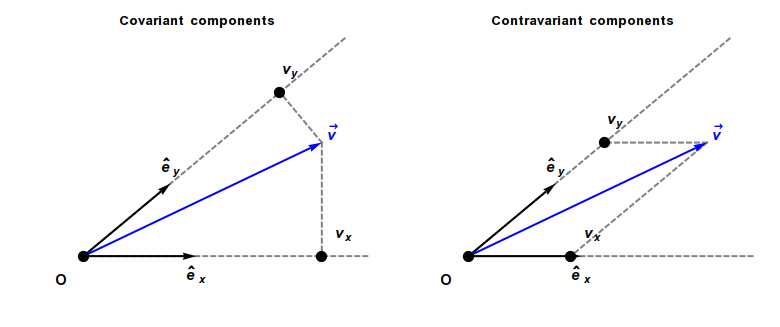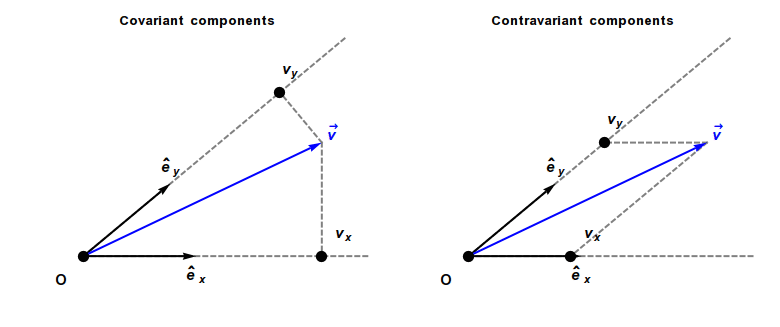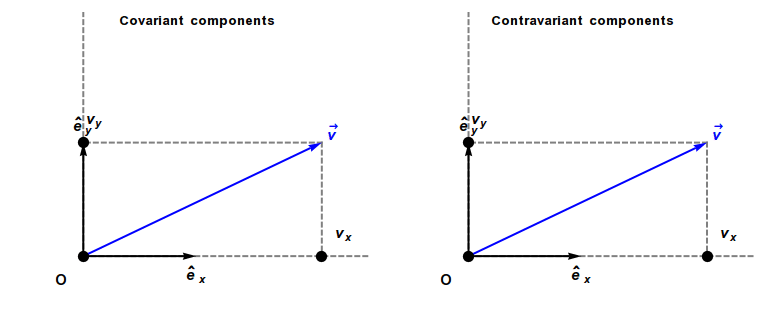
To do this we need to account for the fact that some quantities behave differently under a change of scale in coordinate system units. For instance, if the vector 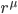 is one meter long, it will have a length of 1 in a coordinate system specified in meters. But if the scale is changed to centimeters, its length will be 100. The same will apply to angles. The vector itself remains the same—what has changed is its representation in a rescaled coordinate system. Quantities that behave this way are said to be contravariant because their size will vary counter to variations in the scale of units they’re represented with.
is one meter long, it will have a length of 1 in a coordinate system specified in meters. But if the scale is changed to centimeters, its length will be 100. The same will apply to angles. The vector itself remains the same—what has changed is its representation in a rescaled coordinate system. Quantities that behave this way are said to be contravariant because their size will vary counter to variations in the scale of units they’re represented with.
On the other hand, there are quantities such as gradients for which this isn’t the case. A 6% grade is a 6% grade whether we specify it in meters/meter or cm’s/cm, so rescaling coordinate systems will vary length specifications along any coordinate axis, but not the gradient in that direction. The metric tensor 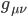 is such an object. As we’ve seen, it’s effectively a generalized dot product between local coordinate system axes. Since its components give their projections onto each other, it behaves like a gradient under coordinate system transformations. Quantities like this are said to be covariant because they retain their values regardless of how their coordinate system scale is varied. The difference is shown in Figure 10 (Wikimedia, 2018).
is such an object. As we’ve seen, it’s effectively a generalized dot product between local coordinate system axes. Since its components give their projections onto each other, it behaves like a gradient under coordinate system transformations. Quantities like this are said to be covariant because they retain their values regardless of how their coordinate system scale is varied. The difference is shown in Figure 10 (Wikimedia, 2018).
Figure 10
This may seem like hair-splitting, but when we move from the realm of absolute flat spaces to that of curved geometries, the difference matters. Some quantities like vectors, lend themselves to a contravariant description whereas others, like gradients, lend themselves to a covariant one. In the parlance of general relativity, it’s customary to specify the indices of the former with superscripts (“upstairs”) and the latter with subscripts (“downstairs”). Each type of tensor can be converted into the other by multiplying with an appropriately dimensioned factor (which is referred to as “raising or lowering indices”), but things are a lot clearer when we stick to representing each in the form that is most natural to them. As such, objects like vectors whose specifications vary under a rescaling multiple coordinate axes are typically specified with “upstairs” indices and those like the metric that behave more like gradients use “downstairs” ones.
With these qualifications, let’s revisit our earlier parallel transport experiments and put some flesh on the bones. In Figure 9 we saw that in Freddy’s universe, 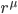 and
and 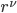 will be the same everywhere and so will
will be the same everywhere and so will 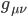 . It makes no difference where (or when) we place any coordinate system. But what about Cathy’s universe? At point A, a small surrounding region will be approximately flat and represented by a tangent plane containing
. It makes no difference where (or when) we place any coordinate system. But what about Cathy’s universe? At point A, a small surrounding region will be approximately flat and represented by a tangent plane containing 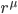 ,
, 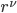 centered on it (Figure 11). Now, let’s define a third tangent vector
centered on it (Figure 11). Now, let’s define a third tangent vector  along our parallel transport path from A to B.
along our parallel transport path from A to B.
Figure 11
Once again, we walk the path from A to B in the direction 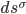 as in Figures 5 and 6, carrying the tangent plane and
as in Figures 5 and 6, carrying the tangent plane and 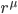 and
and 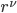 with us (Figure 12).
with us (Figure 12).
Figure 12
At each point in the path, 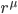 ,
, 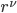 , and
, and  are still oriented in the same directions with respect to any local coordinate system, and the latter remains parallel to the path we’re travelling. When we arrive at B, we see that things still look the same to us as they did when we started. But this time the local tangent plane and coordinate systems we carried with us have twisted with respect to where they were at A and no longer looks the same to an observer who stayed behind.
are still oriented in the same directions with respect to any local coordinate system, and the latter remains parallel to the path we’re travelling. When we arrive at B, we see that things still look the same to us as they did when we started. But this time the local tangent plane and coordinate systems we carried with us have twisted with respect to where they were at A and no longer looks the same to an observer who stayed behind.
In Freddy’s universe, one tangent plane uniquely spans the entire space. All distances and angles look the same from any reference frame within it, and carrying vectors such as 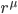 and
and 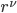 from one point to another is just a matter of summing displacements along any given path between them. But in a curved space like Cathy’s, we need a mathematical object that not only describes displacements along a path, but also one that maps that path onto the local tangent planeas it rolls across the curved surface as shown in Figure 13 (Wikimedia, 2023).
from one point to another is just a matter of summing displacements along any given path between them. But in a curved space like Cathy’s, we need a mathematical object that not only describes displacements along a path, but also one that maps that path onto the local tangent planeas it rolls across the curved surface as shown in Figure 13 (Wikimedia, 2023).
Figure 13
This object, which mathematicians refer to as an affine connection, allows us to describe vectors along any path through a larger curved space in terms of a fixed coordinate system within the local tangent plane at any point. An infinite number of such connections are possible but there is one, known as the Levi-Civita connection, that is a natural choice for spaces that have a well-defined metric tensor at every point because it allows us to define a derivative (or rate of change) along a curved space path that generalizes the usual mathematical rules of vector calculus in locally flat tangent plane regions to the larger curved space. This covariant derivative (which we denote with the nabla symbol 4) will need to have two parts and is given by,
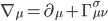 [Eqn. 5]
[Eqn. 5]
For an infinitesimal displacement along any path, the first term on the right is the gradient with respect to the local tangent plane as defined in the usual flat space manner. The second term is the rate at which the tangent plane itself (and the covariant metric tensor embedded in it) is changing in the direction of a contravariant displacement 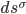 in the direction of a tangent vector to the path. As such, it will be matrix function with three indices, two of which are best represented as covariant and a third contravariant one which we will denote with the index
in the direction of a tangent vector to the path. As such, it will be matrix function with three indices, two of which are best represented as covariant and a third contravariant one which we will denote with the index 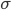 . This function, which per convention we designate with a capital Greek Gamma, is known as a Christoffel symbol. Since it requires three indices to fully capture the evolution of the metric tensor, in Cathy’s space it will have 23, or 8 components to her metric tensor’s 4. We refer to Christoffels as “symbols” because they aren’t true tensors in that they aren’t globally frame-independent until multiplied by an infinitesimal displacement in at least one direction. And as shown, equation 5 doesn’t make sense because the indices on the right and left sides don’t agree with each other. More properly, it defines a mathematical operator that must act on something to produce a meaningful equation. Applying it to
. This function, which per convention we designate with a capital Greek Gamma, is known as a Christoffel symbol. Since it requires three indices to fully capture the evolution of the metric tensor, in Cathy’s space it will have 23, or 8 components to her metric tensor’s 4. We refer to Christoffels as “symbols” because they aren’t true tensors in that they aren’t globally frame-independent until multiplied by an infinitesimal displacement in at least one direction. And as shown, equation 5 doesn’t make sense because the indices on the right and left sides don’t agree with each other. More properly, it defines a mathematical operator that must act on something to produce a meaningful equation. Applying it to 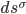 gives,
gives,
 [Eqn. 6]
[Eqn. 6]
With the upstairs and downstairs  in the second term cancelling, this equation is now consistent across indices and the Christoffel term behaves like a tensor. This path derivative will look the same from every coordinate system in Cathy’s curved space. In flat spaces like Freddy’s, the tangent plane is the same everywhere and unchanging so the Christoffel term will vanish leaving us with the usual Euclidean directional derivative we learned in first-year vector calculus.
in the second term cancelling, this equation is now consistent across indices and the Christoffel term behaves like a tensor. This path derivative will look the same from every coordinate system in Cathy’s curved space. In flat spaces like Freddy’s, the tangent plane is the same everywhere and unchanging so the Christoffel term will vanish leaving us with the usual Euclidean directional derivative we learned in first-year vector calculus.
For today’s purposes we needn’t worry about how these equations were derived. The important thing is to understand why curved spaces require these kinds of mathematical tools rather than the familiar ones of Euclidean geometry, and how they reflect curvature in multiple dimensions without additional dimensions to “curve into.” If you’re like me, the latter point is the biggest stumbling block. It’s one thing to know that curved spaces are mathematically possible without additional background dimensions. But it’s another thing altogether for three-dimensional Euclidean space beings to visualize them. Space (or spacetime) can be curved in one of two ways: positive, or negative.5 Positively curved space is spherical and, if extended far enough, finite and closed. In our previous example, Cathy’s universe is a spherical one. And as we saw, the interior angles of a triangle in such a space add to greater than 180 degrees. Her space is finite in size, and travelling in a straight line in any direction will eventually return you to where you started from. Negatively curved space is saddle-shaped and has hyperbolic geometry. The interior angles of a triangle in it would add to less than 180 degrees, and like flat Euclidean space, it extends to infinity in all directions. Figure 14 shows both as compared to flat space.
Figure 14
It’s easy to visualize two-dimensional curved spaces like these in isometric views that show their contours in an additional dimension. But what would they look like where there was none?
In the case of a positively curved space, we can’t do this because there is no way to represent a path that returns to where it started in the same number of dimensions.6 But for negatively curved spaces that extend to infinity, we have a visual example in the art of 20th Century Dutch graphic artist M.C. Escher. Among other things, Escher was known for artistic renderings of mathematical concepts including symmetries and tessellation. His Circle Limit collection of wood carvings depict repeating image patterns whose changing shapes from the center outward are a tessellation of hyperbolic geometry on a disc into right triangles. His 1959 work Circle Limit III (Figure 15), widely regarded as the best in the series, does this with patterns of fish.
Figure 15
There are many ways to tessellate geometric spaces and none are perfect, including this one. But if Cathy’s two-dimensional space was negatively rather than positively curved, this would be a reasonable representation of how it would look to her. If she walked a parallel transport path through it as in figures 5-8 taking the size and orientation of the fish as indicative of distances and angles, upon returning to where she started, she would find that the distances and interior angles she traced would be like those in the negatively curved saddle in figure 14. And if she travelled a straight geodesic path in any direction indefinitely, she would asymptotically reach infinity as she approached the rim. The disc is two-dimensional, but the geometry embedded in it behaves as though it were a saddle-shaped sheet in three dimensions even though the third dimension isn’t there. The underlying mathematics of its hyperbolic (saddle) geometry are embodied in Equation 6. And while we have until now restricted ourselves to two-dimensional spaces for ease of illustration, notice that the indices in its terms can assume any number of values, not just two. As such, it generalizes to any number of curved dimensions, none of which need any “higher” dimension/s to curve into.
There is, however, one dimension that we’ve conspicuously ignored until now… time. We live in a universe where not only length, breadth, and height can be curved, but duration can be as well, and curved spacetime ups the ante in several important respects that we’ll dive into in Part II. So, stay tuned!
Curvature II: Spacetime
Footnotes
1) In mathematics, tensors are matrix functions that define a multilinear relationship between sets of objects in a vector space that preserve their identity in any coordinate system or transformation. Vectors can be thought of as a one-dimensional tensor (that is, a tensor with only one column or row). The dimensionality of a tensor’s matrix array (as specified in the number of indices it requires) is referred to as its rank  , and the number of components it will have in an N-dimensional space is given by
, and the number of components it will have in an N-dimensional space is given by 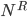 . Thus,
. Thus, 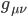 is a rank 2 tensor that in Freddy’s 2-D space will have four components, and in our 4-dimensional spacetime has 16.
is a rank 2 tensor that in Freddy’s 2-D space will have four components, and in our 4-dimensional spacetime has 16.
2) Strictly speaking, the metric tensor isn’t really a true dot product. Rather, it is a generalization of the familiar dot product of Euclidean geometry to the pseudo-Riemannian geometry constrained by special relativity, where time behaves differently than space (more on this in Part II). But for our current exploration of 2-D spatial curvature, this needn’t concern us.
3) Mathematicians refer to this as an orthonormal basis that spans the space.
4) In mathematics, the nabla symbol (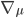 ) is known as the Laplace operator. It is a shorthand reference for the gradient (first derivative) in the direction of a vector defining the
) is known as the Laplace operator. It is a shorthand reference for the gradient (first derivative) in the direction of a vector defining the 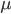 coordinate system; That is,
coordinate system; That is, 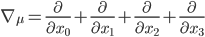 where the index
where the index 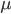 = 0, 1, 2, 3. This representation of a gradient in a particular direction is also referred to as the vector’s divergence.
= 0, 1, 2, 3. This representation of a gradient in a particular direction is also referred to as the vector’s divergence.
5) The reasons for this are mathematical and beyond the scope of this discussion.
6) This is because spherically curved space has a different topology than flat and negatively curved spaces. In mathematics, topology is the study of a manifold’s geometric properties that are preserved when it is stretched or deformed without cutting or sewing, opening or closing holes, or passing it through itself. Negatively curved space has the same topology as flat space because a flat rubber sheet can be stretched to form a saddle. By contrast, a positively curved space cannot be flattened or deformed into a saddle without cutting and forming edges (e.g. – a Mercator projection). There is no way to create a flat representation of it that preserves great circle paths that end where they began without encountering an edge. Likewise, a toroid (donut) cannot be deformed into a sphere or a saddle without cutting and sewing edges, so it has a higher-level topology than negatively or positively curved spaces.
References
Heath, T.L. ed., 1956. The thirteen books of Euclid's Elements. Courier Corporation. Online at https://books.google.com/books?hl=en&lr=&id=mvBIAwAAQBAJ&oi=fnd&pg=PP1&dq=euclid+elements&ots=ed2L7zetPz&sig=wPKfMQ22SZvf4gF_83USfDwb0oY#v=onepage&q=euclid%20elements&f=false. Accessed Sept. 28, 2023.
Wikimedia. 2018. Image courtesy of Jacob Bertolotti. Online at https://commons.wikimedia.org/wiki/File:Covariantcomponents.gif. Accessed Sept. 28, 2023.
Wikimedia. 2023. Image courtesy of Silly rabbit, CC BY-SA 3.0. Online at https://commons.wikimedia.org/w/index.php?curid=2615879. Accessed Sept. 28, 2023.

Scott,
Very clear explanation of curvature. Have you thought about writing a book like general relativity for pedestrians?
kashyap vasavada
Thanks Kashyap! I'm too busy with life to now, but in the not-too-distant future I hope to!