I've told you so far that the gravitational field is encoded in a  matrix known as the metric. Here it is, displayed as a nice table:
matrix known as the metric. Here it is, displayed as a nice table:
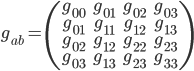
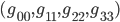 tell you how to measure length-squared along the four coordinate axes. For example, the length along the
tell you how to measure length-squared along the four coordinate axes. For example, the length along the  -axis is given by
-axis is given by 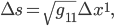
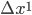 is the coordinate difference in the
is the coordinate difference in the  -direction. The remaining 6 off-diagonal terms keep track of the spatial angle between the coordinate axes. If you know enough Trigonometry, you can figure out that the angle
-direction. The remaining 6 off-diagonal terms keep track of the spatial angle between the coordinate axes. If you know enough Trigonometry, you can figure out that the angle 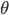 between e.g. the
between e.g. the  -axis and the
-axis and the  -axis is given by this formula:
-axis is given by this formula: 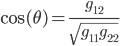
However, I've also said that the metric depends on the choice of coordinates, which is arbitrary. We can use this freedom to choose a set of coordinates where the metric looks particularly simple at any given point. We can start by choosing our four coordinate axes to be at right-angles to each other. This gets rid of all those funky off-diagonal components of the metric, which involve two different directions:
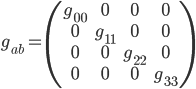
We can also rescale the tick marks along any coordinate axis. This allows us to multiply each diagonal component of the metric by a positive real number. So if say 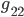 is positive, we can choose coordinates where it's
is positive, we can choose coordinates where it's 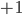 , and if it's negative, we can choose coordinates where it's
, and if it's negative, we can choose coordinates where it's 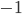 . This gives us:
. This gives us:
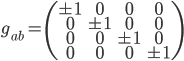
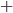 's and
's and  's. This choice is called the signature of the spacetime.
's. This choice is called the signature of the spacetime.
Now if you remember my very first post on spacetime geometry, 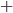 directions in the metric correspond to spatial dimensions, while the funny
directions in the metric correspond to spatial dimensions, while the funny  sign is what makes for a time dimension. But the real world has one time dimension, everywhere. No matter how far you travel, you'll never find a place (so far as we know) where there isn't any time direction, or where there are extra time dimensions. So that means that the correct signature for spacetime has
sign is what makes for a time dimension. But the real world has one time dimension, everywhere. No matter how far you travel, you'll never find a place (so far as we know) where there isn't any time direction, or where there are extra time dimensions. So that means that the correct signature for spacetime has 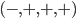 along the diagonal, which is called Lorentzian (a.k.a. Minkowskian) signature. (If we had wanted to describe a timeless four-dimensional space, we would instead select the Riemannian (a.k.a. Euclidean) signature
along the diagonal, which is called Lorentzian (a.k.a. Minkowskian) signature. (If we had wanted to describe a timeless four-dimensional space, we would instead select the Riemannian (a.k.a. Euclidean) signature 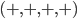 .) We conclude that for any point of spacetime, you can always choose a set of coordinates such that the metric takes a special form that we'll call
.) We conclude that for any point of spacetime, you can always choose a set of coordinates such that the metric takes a special form that we'll call 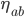 :
:
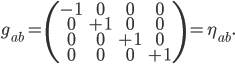
This is related to what Einstein called the Equivalence Principle, which says that at short enough distances, the effects of acceleration are indistinguishable from being in a gravitational field. We all know from personal experience that riding in an elevator can make us weigh more or less, and from TV that astronomers in the Space Shuttle are weightless when they're in free fall. In other words, you can always choose a coordinate system in which there is no gravitational force at any given point.
(Lewis Carroll actually described this principle several decades before Einstein in Sylvie and Bruno, which includes a description of a tea party taking place in a freely-falling house. Then he describes what happens if the house is being pulled down with a rope faster than gravity would accelerate it, and explains how you could have a normal tea party as long as you have it upside-down. I like this book better than his more famous classics, but don't read it unless you can withstand LD20 of Victorian sentimentality about fairy children. Also, Carroll didn't go on to discover a revolutionary theory of gravity based on this principle.)
It might seem now like everything has become too simple. If the metric looks the same at every single point, then why did we even bother with it? Where's the information in the gravitational field? Well, it's true that for any one point, there's a coordinate system where the metric looks just like 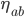 . But there's no coordinate system for which the metric looks like
. But there's no coordinate system for which the metric looks like 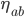 everywhere at once. (Unless there's no gravitational field anywhere, in which case Special Relativity is true). If you make the metric look simple in one place, it has to look complicated somewhere else.
everywhere at once. (Unless there's no gravitational field anywhere, in which case Special Relativity is true). If you make the metric look simple in one place, it has to look complicated somewhere else.
So in order to describe the gravitational field properly, we have to find a way to compare the metric at different points. We can do this using something called parallel transport. I'll give more details later, but basically it tells us how an object moves in a gravitational field when we carry it along a path through spacetime. When we carry the object around a tiny loop so that it returns to its original position, we might find that it comes back rotated compared to its original orientation. If so, we say that the spacetime contains curvature. If the spacetime contains curvature, this is a fact about the gravitational field which is invariant, i.e. objectively true. You can't eliminate it just by changing your coordinates.

You used "it's" wrong...love, Mom the linguist
[not anymore--Aron]
Hi Dr. Wall,
This is a very nice blog you have here - a truly enjoyable read. Thank you very much for taking the time to elucidate complicated physics, and share your thoughts on theology - I have found both very helpful.
Your comments on the signature of a metric got me thinking about something that's been bugging me for a while. In particular, does the signature of a metric correspond to whether its (diagonal) components in a given basis are positive or negative? The main reason I ask is because the Schwarzschild metric (in the usual way it's presented anyway) seems to change its mind if this is the case. In units where c = G = 1, if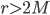 ,
, 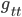 is negative, and
is negative, and 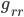 is positive, whereas for
is positive, whereas for 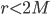 , the converse is true. Does that mean the metric changes from a signature of (-,+,+,+) for
, the converse is true. Does that mean the metric changes from a signature of (-,+,+,+) for 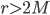 to (+,-,+,+) for
to (+,-,+,+) for 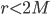 ? Instinctively, I'm pretty sure the answer to this is no, but I'm not sure I understand why. And if the answer is yes, what does that mean physically? Would that mean the temporal and radial coordinates 'switch roles' inside a black hole, or something?
? Instinctively, I'm pretty sure the answer to this is no, but I'm not sure I understand why. And if the answer is yes, what does that mean physically? Would that mean the temporal and radial coordinates 'switch roles' inside a black hole, or something?
Sorry if this question is a little tedious - I'm still a little new to GR, and am trying to get properly to grips with it.
Many thanks and blessings,
Andrew.
Andrew,
In general, the diagonal components of a metric do not tell you anything useful about the signature of the metric. For example, there is a coordinate system where the metric of Minkowksi space is a 4x4 matrix with 0 for each diagonal element and +1 for each non-diagonal element. (Exercise: figure out what are the 4 unit coordinate vectors in this system, visualized with respect to the usual Minkowksi lightcone.)
The signature is a list of signs (+,-,0) and it does not matter in which order they are listed (since one example of a coordinate transform is just to switch the names of your coordinates). Annoyingly, there are different conventions about whether Minkowski space should be (-,+,+,+) or (+,-,-,-); GR people like me tend to use the former but particle physicists sometimes use the latter.
To find the signature of the metric, you have to find a coordinate system where the off-diagonal terms are zero (or suffciently small compared to the diagonal terms that they don't flip the signs). But there are a couple of tricks which can be useful. One is to take the determinant of the metric (usually written as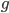 ): since the sign of the determinant is invariant under coordinate transformations, this at least tells you whether the number of minus signs in the signature is odd or even. (The square root of the determinant
): since the sign of the determinant is invariant under coordinate transformations, this at least tells you whether the number of minus signs in the signature is odd or even. (The square root of the determinant 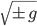 is the thing you integrate to get the spacetime volume of a region, by the way). Another thing to notice is that if there are any (nonzero) vectors whose inner product with themselves is zero, then there are lightlike directions, so clearly we don't have Euclidean signature. The same goes if there are any vectors with negative self-inner-product (unless it might be the (-,-,-,-) evil twin of Euclidean signature; to rule that out you'd look for a vector with positive inner product.)
is the thing you integrate to get the spacetime volume of a region, by the way). Another thing to notice is that if there are any (nonzero) vectors whose inner product with themselves is zero, then there are lightlike directions, so clearly we don't have Euclidean signature. The same goes if there are any vectors with negative self-inner-product (unless it might be the (-,-,-,-) evil twin of Euclidean signature; to rule that out you'd look for a vector with positive inner product.)
The fact that the Schwarzschild coordinates go funny at the horizon is just an artifact of the coordinate system; there are other coordinatizations of the Schwarzschild metric, such as Eddington-Finklestein, Kruskal–Szekeres, or Gullstrand–Painlevé, where things behave more regularly as you cross the horizon. For a good understanding of the interior of a black hole, you should be comfortable with these different coordinate systems (and know which coordinate regions are physical in the case of a black hole that formed from collapse).