Last time I discussed the cosmological implications of the regular-old Ordinary Second Law. Now I want to discuss what happens if you use the Generalized Second Law instead—this being a generalization of the Second Law to situations involving black holes and other horizons, which seem to have an entropy proportional to their surface area.
I started thinking about this issue after Sean Carroll gave a colloquium at U Maryland about the Carroll-Chen model, and the Second Law, back when I was a grad student.
From my perspective, the important thing about that colloquium was that it got me thinking about refining the classic argument that the Second Law predicts a beginning. I said to myself something like the following:
"Self, for the past couple years you've been spending all of my time thinking about the Generalized Second Law (GSL), that wild new version of the Second Law which applies to causal horizons. Well, there are horizons which appear in our own cosmology (because of the accelerating expansion of the universe). So can we make this argument using the GSL instead of the Ordinary Second Law (OSL)? And if we do, will it make the argument stronger or weaker?"
Well, when I thought about it a little bit, I realized that you could use the GSL in two distinct ways to argue for a beginning. One of them is a quantum generalization of the Penrose singularity theorem, which I discussed here. The other way is a generalization of the Argument from the Ordinary Second Law, described above. Both of these uses of the GSL are discussed in my article, but it is important to realize that they remain two distinct arguments!
Fine-grained vs. Coarse-grained. The reason is that there are actually two subtly different ways to formulate the GSL. You see, the entropy is a measure of our ignorance about a system. To exactly define it, you need to make a list of the things you are allowed to measure about the system (e.g. the pressure and temperature of a box of gas), and then the entropy measures how much information content is in the things you can't measure (e.g. the positions or velocities of individual molecules). The procedure of ignoring the things we can't measure is called coarse-graining (because it's like looking at a grainy photograph where you can't see all of the information in the object).
Technically then, there's some ambiguity in the definition of the entropy, since the intitial step where we list what we can measure is a little bit ambiguous. Fortunately, since the amount of information we can't measure is much larger than the information we can, this doesn't usually matter very much. Quantitatively, the different ways of defining entropy give pretty close to the same numerical answers.
But we could pretend that we could measure everything about the box of gas to arbitrary accuracy. The only uncertainty allowed which could produce a nonzero entropy is uncertainty about the initial conditions. This is called the fine-grained entropy, and while it has the property that it neither increases nor decreases as time passes. Since the fine-grained entropy can't decrease, it technically obeys the Second Law, but in a really boring and stupid way.
The distinction becomes important when you start talking about black holes and the GSL. Suppose you have a star orbiting a black hole. Matter from the star is slowly getting sucked off the outer layers of the star, and getting sucked into the black hole. (This is a realistic scenario which is believed to really occur in some solar systems, by the way!)
Well, we have a choice. We could use a coarse-graining to describe the entropy of the star. In that case, the entropy would go up for 2 distinct reasons: A) because stuff is falling into the black hole making its area increase, and B) because ordinary thermodynamic processes are happening inside the star, making the entropy increase for usual non-black-holey reasons.
Or, we could take the fine-grained point of view, and pretend we know everything about the matter outside the event horizon. In that case, the entropy increases only because of (A), things falling across the horizon. Stuff happening inside the star doesn't make a difference. This would be the fine-grained GSL, and it is nontrivial—the entropy defined in this way can go up, but not down. You could say, that the only coarse-graining we use is to forget about anything that fell across the horizon, and this is enough to get a nontrivial result. (This was pointed out by Rafael Sorkin.)
In my dissertation research, I proved the GSL in the fine-grained sense. This was very useful since there are still some thorny and unresolved issues of interpretation with the Ordinary Second Law due to the exact meaning of coarse-graining. The fact that one can avoid this issue in discussing the GSL made my life much easier!
Also, coarse-grained versions of the Second Law are only true if you have a history with a well-defined arrow of time—i.e. a universe that is constrained to begin with low entropy, but has no particular constraint on how it has to end up. The fine-grained GSL, on the other hand, appears to be true for all states and therefore has no dependence on the arrow of time. As a result, you can even apply the fine-grained GSL backwards in time if you want to, and this is perfectly OK, even though we normally think of the Second Law as something which only works in one time direction.
The forwards-in-time GSL applys when you have a worldline (an "observer", if you feel like anthropomorphizing) which extends infinitely far to the future. It says that the boundary of what the observer can see (called a "future horizon") has increasing entropy. The backwards-in-time GSL, says that if you have a worldline which extends infinitely far to the past (if there are any), then boundary of what they can be seen by (called a "past horizon") has decreasing entropy. Equally true.
How to apply the GSL. If you want to use the GSL as a singularity theorem to show that time ends in the middle of a black hole, you'll want to use the forwards-in-time GSL. But if you want to use it to argue that there was an initial singularity at the Big Bang, you need to use the backwards-in-time GSL. That's what I did to generalize the Penrose singularity theorem in my paper (like the original, it only works if space is infinite).
But I also considered the possibility that you might use the forwards-in-time GSL to argue for a beginning. In this case, it would be a substitute not for the Penrose theorem, but for the OSL. The details are in section 4.2 of my article, but the upshot is pretty much the same as before, that there probably had to be a beginning unless either (i) the arrow of time reverses, or else (ii) the universe was really boring before a certain moment of time.
Why even bother? Other than the fact that the GSL has deeper connections to quantum gravity, the main technical advantage of using the (forwards) GSL is that it is more clear that the entropy reaches a maximum value in our universe (due to the accelerating expansion of the universe at late times, there is a de Sitter horizon at late times whose entropy is about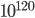 
). This makes it harder to play games with infinities.
Also, if we want to reverse the arrow of time, the GSL indicates that the universe probably has to also be finite in size. That's because, if the universe is finite in size, there is the possibility that before a certain time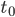 
, everything is visible to an observer, and before that time there would be no horizon at all. That would make the fine-grained GSL trivial, forcing us to use the coarse-grained GSL. That's important because it's only the coarse-grained GSL which depends on the arrow of time.
But mainly I just wanted to see if the standard argument from thermodynamics would still work when I rephrased it in terms of horizon thermodynamics. Not surprisingly, it does.
(On the other hand, the connections to the Penrose singularity theorem are much more surprising, and I believe that it is telling us something deep about the laws of quantum gravity.)
Hi Aron,
I recently read an article you wrote on Scientific American where you apply the GSL to show that a time machine contradicts this law, and so can't actually be built according to the GSL. http://blogs.scientificamerican.com/critical-opalescence/2014/05/23/time-machines-would-run-afoul-of-the-second-law-of-thermodynamics-guest-post/#respond
However, in your counter example you assume that the the horizon of the Close Timelike Curve would be infinite in the past (thus having infinite entropy which can't be matched by the finite entropy in the future). My question is what allows you to make this assumption?
Sincerely,
Edger
Dear Edger,
If you are just trying to build a time machine in the laboratory, then to a good approximation you can think of the system (e.g. the Earth or perhaps the Solar System) as just sitting inside of an infinite space. It would follow that as the horizon goes out into infinite empty space, it goes back infinitely far in time. This is just an approximation: in reality space outside the Solar System is not empty, afte that you would eventually hit the Big Bang singularity. But it's still a very good approximation for a long way out, so the entropy of the horizon would get really really big.
I answered a similar question in the comments section to my original post on this topic:
Pingback: The Cosmological Argument for the existence of God | Existential Stuff
Wow, Aron! I just discovered your blog this week. Great job - I'm a non-physicist just trying to defend the Christian faith as best as I can and you really do well in making this stuff comprehensible. I'll be returning often! Thanks!
Welcome, Brent, and thanks for your comment!
Im wondering if you can elaborate on the relationship to the theory with infinity. Am i right to say that to apply the GSL to argue for a big bang singularity requires the universe to be spatially infinite?
A lot of physicists say that singularity is not something real because it is badly behaved infinite. In other words, they dont mind space being infinitely big as long as it doesnt go from finite size to infinite size in a finite amount of time. but they do object to the density of the universe going from a finite number today to an infinite number at the big bang. As this would make a disocnontious jump i.e a badly behaved function. As the latter is realised in the singularity most physicists have a big problem with singularities.
are these fair descriptions or have i gone wrong?
howie,
No physical quantity can be an actual infinity. As a physical quantity such as density increases without limit, at some point the current equations become invalid, and a more accurate model is required. In that more accurate model, the physical quantity does not become infinite. So, a singularity indicates the requirement for a more accurate model.
There is no actual or physical singularity that could be called a Big Bang. What we have are equations that describe an numerical singularity--as time t->0, the density d->infinity. The numerical singularity indicates that our physics is not accurate as t->0 and a better model is required.
Mactoul, what you have just described is what most physicists say to me. i.e that singularities are not real just a sign your theory has broken down. i think the view is: well if Gr breaks down, so what? We are convinced for other reasons its replaced by a deeper theory anyway. And in the deeper theory there wont be a singularity. But it seems Dr Wall argues there may be a singularity even in the deeper theory . See his paper:
"The Generalized Second Law implies a Quantum Singularity Theorem"
So the question is , if he is right, what does it mean physically? Are we saying the density and other parameters really can become infinite in the sense I described above. If they cant then what happens to them?
howie,
Physicists are typically very sloppy when talking about things like origin of the universe. For the creation or beginning is simply not within the province of physics so they have to smuggle in philosophical assumptions while pretending not to do it. For instance, see this takedown of Stephen Hawking by a professional philosopher
http://maverickphilosopher.typepad.com/maverick_philosopher/2018/03/stephen-hawking-and-bad-philosophy.html
HI Mactoul. I thank you for spending the time to write but I have to say I dont think you have answered the question I have asked. Perhaps it really should be Aron doing that? Instead you have taken the opportunity to slag off Stephen Hawking just as he has died. . The quality of Stephen Hawking philosophical writings has nothing to do with the question i asked and picking the time of his death to throw into the conversation is just very inappropriate.
Pingback: Is there a God? Answering Stephen Hawking Part 2 – Hacking the Gate
Have you ever given a public talk/lecture on this paper/theorem, that's viewable online?
Dear Dr. Wall,
I've never commented on your blog before, but I've been aware of it for years and I've always appreciated how clearly you communicate the various ideas you discuss! I'm a non-physicist who first found your blog because of my interest in the existence of God, so I'm sure I miss a lot of physics-related nuance, but I've gotten an enormous amount of value from reading your posts.
I have a question regarding a claim that I've heard some philosophers make. The claim is roughly that, if we take our universe (or at least everything in the observable universe) and run it arbitrarily far into the future, inflation could restart an arbitrarily large number of times, and sometimes produce regions of spacetime that are indistinguishable from our current observable universe. This scenario wouldn't just imply that inflation may be continuing somewhere outside of our observable universe, but that inflation will eventually restart in the future of areas that we currently observe. Does the GSL permit this?
If I'm reading your paper (The Generalized Second Law implies a Quantum Singularity Theorem) correctly, it's actually impossible to restart inflation in asymptotically flat or AdS spacetime. However, my understanding is that our universe, in the distant future, will be better approximated by de Sitter spacetime, and I have less understanding of what your article implies about de Sitter spacetimes (which is likely just due to my own lack of physics understanding). I know restarting inflation would be incredibly improbable, but does anything definitively stop it from eventually restarting somewhere in the future, and doing so an infinite number of times as we go into the infinite future? If there are an infinite number of observers in the future who see a region of spacetime that looks like our own, does that not also imply that, more likely than not, we ourselves are actually incredibly far away from the true beginning of the universe, and that many Earths/humans/whatever else have already existed?
I think (and, for the sake of my philosophical views, hope) that I've gotten something wrong in the above reasoning, but I need help knowing if/where I went wrong. I apologize if I'm missing anything obvious in your paper or past discussions of this topic.
Thank you for your time!
Thomas
Tom,
Welcome to my blog. This is an excellent question.
1. There is a calculation by Coleman and De Luccia of the odds to "up-tunnel" from a big de Sitter universe to a small inflating de Sitter universe (assume that both are allowed configurations given the laws of physics). The odds are indeed nonzero (though exponentially tiny for it to take place in any given place and time). The probability scales like
where 
is the difference between the generalized entropies of the cosmological horizons of the two de Sitter universes. This is compatible with an entropic interpretation, if you think each de Sitter universe has 
microstates and you are calculating the odds of a transition to the macrostate with a smaller number of microstates. (It also appears to be compatible with my GSL argument as, in the limit that the big dS goes to Minkowski, the probability of up-tunnelling goes to zero.)
2. Although point 1 is generally agreed upon, in my opinion a lot of people aren't visualizing this process correctly. (The Coleman De Luccia calculation is in Euclidean signature, which obscures the Lorentzian spacetime interpretation.) I personally believe that the right way to think of this is NOT that a small region of the big dS, well inside the cosmological horizon, splits off and forms a small dS. Instead, you should visualize it as a very improbable fluctuation where the ENTIRE cosmological horizon has, by chance, a much tinier area than expected.
3. Precisely becauase this process has an entropic interpretation, I don't think it is a good model for the formation of our universe. The problem is the usual one with saying that our universe is a downward Boltzmannian fluctuation from thermal equilibrium, namely that there is no good reason to predict an entire low entropy cosmos, as the downward fluctuation needed to create just a person, or just a planet, is much smaller than needed to make an entire low energy region with many galaxies. So, whether or not these downward fluctuations from big empty dS happen, I don't think we live in one. (The analysis is complicated by the fact that nobody knows how to do probability theory properly in an infinite multiverse. But I am crossing my fingers and assuming that the right way to do epistemology doesn't change the intuitive answer above.)
4. There is a distinct and more popular version of eternal inflation, that is roughly like what you say, but doesn't involve restarting inflation from a big empty de Sitter universe. Instead, the idea is that, as a result of quantum fluctuations, in some regions inflation happens not to end. (This is somewhat similar to the up-tunnelling story but there is no big dS involved.) Then, because those regions grow exponentially, there is always (with probability close to 1) an inflating region, from which new bubble universes are formed. My understanding is that, whether or not this happens, depends on your exact model of inflation (it involves a competition between an exponential decay and expoential growth, and the details of the potential determine which one wins). But, it is certainly one of the more scientifically plausible narratives that could produce a (potentially) infinite multiverse.
5. Like the previous model, this one has the property that possibly: "we ourselves are actually incredibly far away from the true beginning of the universe". (Whether or not this is probable, depends on your view of how to do epistemology in a multiverse. Most formulas for doing this lead to highly counterintuitive paradoxes, so there's probably something basic we are missing here philosophically.) However, I do see an important difference from the previous model, which is here I think the initial conditions still matter a lot for what kind of universe tends to be produced. (If the initial conditions DON'T matter, then necessarily our predictions must be the same as in the maximum entropy universe, which doesn't agree with observation. So the low entropy initial conditions MUST matter. I'd like to turn this fuzzy idea into a paper some day but I'm not sure the right way to say it yet.)
6. From a philosophical/theological point of view, while I don't object to other universes per se, I don't find it plausible that God would create a multiverse of the sort in which each human being is copied infinitely many times. That would seem to me to deprive individual life of meaning. So, I believe he didn't do that. But exactly how this relates to the correct model (whatever it is) of inflation, I obviously don't know. (I also don't believe that God would allow Boltzman brains to exist if they are conscious, but if it turns out that they are not conscious, then maybe it doesn't matter.)
Thank you so much for your response! This is incredibly helpful..
1. I want to make sure I'm interpreting this correctly. Are you saying that, as our cosmological horizon expands, the probability of inflation restarting approaches zero, rather than a specific nonzero value? Would that imply that it's quite possible (and even highly probable?) that our future cosmological horizon will never restart inflation again? I might be misunderstanding, but I interpreted a previous comment from you as saying that the generalized entropy of our future cosmological horizon has a finite maximum value, which I would have thought implied that the chance of up-tunneling approaches a small but nonzero value as time goes to infinity.
Points 2 and 3 are very helpful. I was definitely visualizing the process of restarting inflation incorrectly. Am I correct in thinking that, even if our future cosmological horizon does eventually restart inflation, it wouldn’t be able to birth its own infinite, eternally inflating multiverse? I’ve heard it claimed that such a process is possible (although I don’t remember if the source was credible).
4 and 5. Interesting! I would certainly enjoy reading any further papers you publish about low entropy initial conditions and their importance. I've often heard that universes generated by eternal inflation may have many different physical constants. Is this a largely inevitable result of how eternal inflation works, or is it conceivable for eternal inflation (perhaps with highly fine-tuned initial conditions) to only/primarily bring about universes that are physically very similar to our own?
6. This is a very interesting perspective, and one I want to think about more. I've become very fascinated with whether or not the universe is infinite and how that would interact with the rest of my worldview. It certainly seems possible: I think I’ve read that certain measurements of the CMBR favor models of inflation that are eternal (although I've also read the opposite, so I'm not sure how seriously to take that), and it seems less arbitrary to have an infinite universe than a universe of a specific finite size. I've also heard it argued that God would want to create as many creatures as possible, so that as many creatures as possible could be brought into a loving relationship with God. That seems reasonable to me, though it probably needs some added nuance.
Recently I've become interested in what it would mean for there to be infinitely many copies of me and how I should feel about that. It would be an honor to run my abbreviated ideas by you, but it seems tangential and this comment is already long.
Thanks again!
Tom,
1. No, I'm not saying the probability of inflation restarting from a universe like ours gets closer and closer to 0. What I am saying, is that any resulting new small universe will be "bad" in the sense of being completely chaotic (all states equally probable) so that life and order can appear only by chance. Thus, we have very good reasons to believe that this is not the origin of our own universe. This also means that the scenario you spell out in 2-3 doesn't work.
4.-5. Eternal inflation does not, by itself, lead to "many different physical constants". In order to get that you need a sufficiently complicated theory that there are many possible distinct ground states (vacua) in the model. Imagine, if your inflationary potential has multiple local minima, then a ball rolling around in that potential could end up in different basins... then, if your other matter fields couple to that potential, they could end up behaving differently in different places... perhaps you would even have a completely different spectrum of particles/fields at low energy! So from a low energy perspective, it would seem like different laws of physics, even though the FUNDAMENTAL laws at high energy are actually the same.
But for any simple potential (e.g. a polynomial with low order), there are usually only a small number (perhaps just one) minima (where we count as the "same" mimima that are related by a symmetry, as in the case of the electroweak symmetry breaking). Most candidate theories of physics are not sufficiently complicated to allow enough distinct vacuum states to solve the fine-tuning problem of e.g. the cosmological constant. But, one exception is string theory, where the (various ways) of reducing from 10 or 11 dimensions to 4 dimensions end up being sufficiently complicated, that in that case there do seem to be gazillions of consistent vacua. (These vacua would mostly be metastable meaning that there is a tiny probability to decay to a lower energy vacuum, but the half-life might be longer than the current age of our universe.)
6. From the perspective of fitting the data, the inflation of the universe has to have blown in up by a factor of at least e^60 (sixty e-folds) in order to explain the observed flatness of the universe. But there is not a clear physical need for more inflation that that---it depends on the model, I think. But I'm not enough of a specialist in cosmology to easily estimate how typical it is to have eternal inflation, conditional on having that much. I think it depends on how "flat" the potential is (flatter leads to more e-folds) and also where you start initially.
It seems to me that a work of art is most beautiful if it has unity-in-diversity, that is a variety of different parts that all contribute to some overall whole in a harmonious fashion. For God to simply actualize every possible creature meeting some minimal standard, would achieve diversity but it would not achieve unity. Thus, a cosmos with a large but finite number of beings, who have some common destiny (e.g. being united in Christ) is a more noble goal for God to aim for, compared to a multiverse in which there is no common destiny. Or to make an extreme comparison, the Lord of the Rings as authored by St. Tolkein, is by itself more valuable than the entire Library of Babel.
Feel free to share the ideas here if you like. I don't promise to respond, but it seems topical so others might be interested as well.