Our best theory of gravity is classical General Relativity. "Classical" is physics-speak for not taking into account quantum mechanics. So we know that classical GR has to break down during the Planck era, if not later.
Classical Big Bang cosmology predicts that there is an initial singularity at the first moment of time. In fact, there are some theorems to that effect. These are the Penrose and Hawking singularity theorems, which will be the subject of this post.
In GR, attractive gravity is caused by the energy or pressure of matter. Tension (which is negative pressure) produces antigravity (repulsion rather than attraction).
Very crudely speaking, the singularity theorems say that if you assume that matter obeys some energy condition restricting the amount of energy and/or pressure, then you can deduce that under certain conditions there has to be a place where your spacetime has an edge and cannot be extended any further. This we call a singularity. Typically, some component of the curvature becomes infinite at the singularity.
There are several different singularity theorems, pioneered by Hawking and Penrose. One of them says that singularity theorem says that all expanding cosmologies like our own have to begin with a singularity. Roughly speaking, it says that if there is only gravity and no antigravity, then tracing the universe backwards in time there is no way to stop it from crunching down to zero size. Hence there must exist an initial singularity (at least somewhere, perhaps everywhere).
However, this Hawking-Penrose theorem uses something called strong energy condition, which says that the repulsive antigravity from tension is not allowed to be greater than the gravity from energy. It turns out that the strong energy condition can be violated by lots of different types of otherwise reasonable physics theories. In particular, it was violated during inflation, and it is violated by the cosmological constant today. So no one really takes this theorem very seriously anymore.
There is another singularity theorem (proven originally by Penrose) which is better, because it only uses the null energy condition, which says that nearby lightrays are always focused by gravity. This turns out to be a much weaker condition, which is satisfied by most respectable classical matter theories (although it is violated quantum mechanically). However the Penrose singularity theorem only says that there has to be a singularity if space at one time is infinite.
If space at one time is finite in size (for example, if it is shaped like a 3-sphere) then there might be a "bounce" where the universe contracts to a small size and then starts expanding again. The de Sitter cosmology is an example of this, although there are also examples of finite cosmologies that begin with singularities. We don't really know whether space is finite or infinite, since inflation stretched it out so much that even if it were a giant sphere, the radius is so large that it seems flat today.
A few years ago I wrote an article in which I argued that the conclusions of the Penrose singularity theorem should continue to hold in quantum gravitational situations. Even though the null energy condition can be violated by quantum fields, it turns out that you can get the same conclusions if you instead assume something called the "Generalized Second Law" (GSL), which says that the Second Law of thermodynamics applies to black holes and similar types of horizons.
(I described the application of this result to time travel in a recent Scientific American blog post. Technically, you have to use the time-reverse of the GSL, which I mentioned in the comments here, but if the GSL is true, its time-reverse should also be. This may seem weird because normally we think of the Second Law as something which only works in one time direction, but I promise you that one can make sense of it.)
The advantage of using the GSL is that it makes it more plausible that the conclusions of the Penrose singularity theorem apply even in fully quantum-gravitational situations, e.g. during the Planck era. In my article, I showed that the results apply "semiclassically", meaning when the quantum corrections to spacetime are small but still taken into account. I then argued (and not everyone would find this part of my article persuasive) that under certain assumptions one might expect the result to hold even in full quantum gravity, when these quantum fluctuations are large. But remember, all statements about quantum gravity are speculative.
I am a little reluctant to even bring up my own work, since personally I think it is more persuasive that clearly established (but incomplete) physics predicts a beginning, than that speculative new physics says this. I think of it more as laying the groundwork for a possible future understanding, then a totally conclusive result. Still, I think that the Penrose theorem is connected to enough other deep principles of physics that something like it will probably be true and important in the final theory of physics. Other physicists think that singularities are so disturbing that any "complete" theory of physics should eliminate them.
Funny story. One time I was arguing with an atheist grad student about God and the question of the universe's beginning came up. I mentioned my own work (and I am quite sure that I put in some caveats about the potential limitations, since I always do this). A few weeks later I found him posting on some atheist website cocky statements along the lines of "Theists believe that the universe had a beginning because of the GSL, but this is silly for the following reasons...". And this at a time when practically no one else had even heard of my work! So just in case it isn't clear: many smart people believed in God before I came along, and the case for Theism is hardly dependent on my tiny contributions to physics!
In conclusion, to the extent that the singularity theorems are relevant, they tend to point to a Beginning, although it might be possible to evade this conclusion either by (a) having space be finite, or else (b) through quantum gravity effects, if my speculative arguments for a quantum singularity theorem are wrong.
Dear Aron: Singularities and Infinities are the heart of the Big Bang cosmology. These are not only mathematical conundrums, they are unphysical. Planck in 1900 solved the ultraviolet catastrophe by finding the Quantum of Least Action, the smallest physical quantity. Let us set h=1 and use integers to build physical objects. Look at the Kretschman Invariant. It has radius in the denominator. Set r=0 and there's your singularity. But r=0 is arbitrary and unphysical. Get rid of r and replace it with something physical, n-sub-h, a large finite number of quantum particles. This is an object, a Supermassive Black Hole, made of a large finite number of quantum particles. Neutrinos, by Pauli Exclusion and Heisenberg Uncertainty, will assume an unbreakable degenerate state. There are more reasons why neutrinos can be considered the ultimate fundamental particle and I would be happy to discuss this with you.
Dear Roy,
Thanks for your comment. With respect to singularities, you're in good company; there are a lot of physicists who agree with you that singularities must be unphysical. But I think this a somewhat of a prejudice and we shouldn't just assume it without proof. Sure, there are other examples in physics where singularities in one theory get resolved by a better theory. But in the case of e.g. the ultraviolet catastrophe, the infinity would have spoiled the experimentally measurable atomic theory. I don't think the same can be said for singularities inside of black holes.
(One should perhaps distinguish between a singularity as (a) infinite curvature or (b) an edge of spacetime. In a theory of quantum gravity one might perhaps have (b) without (a), especially if spacetime is actually discrete.)
There is a famous calculation due to Chandrasekhar which calculates whether a star can be held up by the degeneracy pressure due to the Pauli Exclusion principle. This calculation does not support the idea that neutrino degeneracy pressure prevents the singularity. Anyway, in the Standard Model of particle physics, the neutrino is no more or less fundamental than the electrons or quarks.
I'm guessing you don't actually have a well-defined mathematical model for the behavior of these "large finite number of quantum particles". I was just arguing in another comment that not everything in life can be mathematized, but I think that if you are trying to do physics, then at the end of the day you need to have some type of mathematical model, not just a word-picture. It's unlikely---forgive me for being blunt---that a person will be able to construct this model unless they have solid grounding in the best current models of physics.
It seems to me that there are two appraoches going on here. One is to try and make singularity theoroems more general. The other is to try apply what we think we know about quanutm gravity candidate theories to the big bang and see what happens. What I think is often an exciting devleopment in theorietical physics is when two very different appraoches come to the same answer. However it seems to me these different appraoched are not converging as we see many claims that singualrities are resolved in these quantum gravity candidate inspired models. Do you agree?
sp,
There are certainly several such claims, but I personally don't take them as seriously as I take the GSL.
Take for example loop quantum cosmology. In my own view, loop quantum gravity is not a mature enough subject to be able to start talking about cosmology yet. Basically loop quantum cosmology is a descendent of "minisuperspace" models, where you only try to quantize finitely many degrees of freedom of the universe (e.g. just the overall scale factor as a function of time). The original quantum-GR minisuperspace models indicated there was still a beginning, but apparently if you quantize in a sort of LQG-inspired way you can construct bouncing cosmologies. Anyway, there are severe problems trying to even define the dynamics of loop quantum gravity, and I doubt that LQC has much relevance to what the fully quantized theory (the one with local degrees of freedom) would say.
String theorists do talk about "singularity resolution", meaning that certain spacetimes which are singular from the perspective of point particles turn out to be OK from the perspective of propagating strings. But there are other types of singularities which are not known to be resolved in string theory. For example, I don't think there is any widely-accepted string model which resolves the singularity inside of a black hole. To the best of my knowledge (although I am not really an expert in this area) the type of singularities which string theory resolves are not the same type as those that the Penrose singularity theorem would predict.
(I know that some people explore string theory models of pre-Big-Bang spacetimes,e.g. the "string gas csomology" of Brandenberger and Vafa. I don't understand these models in any detail, but I know that Brandenberger-Vafa take space to be finite, so that doesn't contradict the conclusions of the Penrose theorem. In any case, this is just one possible scenario, not a statement about what always happens in string theory.)
So my tentative expectation is that my results are compatible with string theory. I am fortified in this conclusion by the fact that you can also use the GSL to predict several other types of constraints on valid spacetimes (e.g. no traversable wormholes or warp drives). Interestingly, it turns out that these conditions on the spacetime are also needed for the consistency of AdS/CFT (a version of the holographic principle) which is a pretty well-explored aspect of string theory these days. So I think everything fits into a consistent picture, although I repeat once more that all statements about Planck era quantum cosmology are speculative.
Dr. Wall, I have recently stumbled upon your website after browsing the Reasonable Faith Q&As and finding a link to your article on Quantum Eternity Theorem. I had a question for you concerning a recent objection I heard concerning the singularity of the universe. I have the link attached at the bottom; please give it a watch, it's only a few minutes. To sum up, basically what they say is that the singularity and the Big Bang are horrible misnomers, and really space is infinite, and our observable universe was once condensed into a super hot dense state (I just got the theme from the Bib Bang Theory in my head), which then expanded into the infinite space. He also claims that this works even if space itself is finite and then lists some complex equations that he doesn't bother to name or go into (something about the infinite metric curvature of spacetime?). To top it off, he shows a model of the universe that may have had a "before" the Big Bang, which condensed into what we think of as the singularity and then expanded back into the universe we know today. Because no specifics were listed, I don't know if you have covered this before, but I am particularly interested in your comments on infinite space, specifically the part at 2:00 in where it talks about finite infinite space.
For me, as a layman, the best I can come up with to counter such assertions would be, for the infinite aspect of it, to posit that actual infinities are incoherent and impossible in the real world., though they may work in the mathematical world. Could you comment on this aspect of infinite space?
As for the second, the best I can do is to think about thermodynamic equilibrium and that given infinity, we would have already reached that.
Here's the link:
https://www.youtube.com/watch?v=q3MWRvLndzs
Also, this supplements the infinity aspect around 4:00:
https://www.youtube.com/watch?v=XBr4GkRnY04
I would appreciate your feedback and comments.
To my comment in parenthesis, it's the infinite differentiability of the metric of spacetime. My apologies.
Welcome Nick,
Thanks for your question. But I wonder that you are trying to learn physics from videos that "[don't] bother to name or go into" crucial details. Maybe you should try to find some websites or books which go into better detail. Also I'm not sure why you are trying to "counter" these assertions that you don't yet understand. (Do they seem to contradict something you believe?) It's always dangerous to try to refute something until you've first understood it. If the videos aren't clear enough to be understood, I think you'd be better off turning to other sources.
The video's points about the "Everywhere Stretch" and the "We don't know what we are talking about" are based on decent points, and the description of an infinite space expanding into itself is okay. But it really falls over backwards when trying to explain how a finite universe could expand, which it claims is based on supertechnical math.
Really it is not as hard as the video makes it out. We don't know whether the space is finite or infinite, but if it were finite it could have the geometry of a sphere, or some other shape. (Important: when math or physics people talk about a sphere, we mean what normal people would call the surface of the sphere, not the interior! If we wanted to include the interior, we would call it a ball). So an ordinary sphere is called a 2-sphere because the surface is 2-dimensional. Really if space is sphere-shaped it would have to be a "3-sphere" or hypersphere, since space is 3 dimensional. But to get some intuition you can imagine everything one dimension down, and imagine that the universe is a regular sphere or "2-sphere".
So imagine a sphere which is getting bigger and bigger in size with time, like a balloon being blown up. If we paint a bunch of galaxies on the balloon, they will each get farther and father away, but none of them is special, since all of the distances along the balloon are increasing proportionally. One more thing. Only the surface of the sphere is real! The interior and exterior don't really exist. The only thing that this balloon metaphor is the intrinsic geometry of the surface of the balloon itself, the third radial direction is irrelevant and doesn't exist.
And no, this sphere would not be finite and infinite at the same time. I think the video only meant that, like the infinite plane, we can talk about the sphere getting bigger without there being any extra dimensions for it to expand into.
So what was going on with all that blather about "infinite differentiability of the metric?" Really something kind of stupid and artificial described in most GR textbooks, which has nothing to do with the expansion of the universe. If you actually want to do calculations on this sphere geometry, you might conceivably be so horrible as to want to write the geometry in terms of two coordinates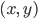
(in the real world it would be 3 space coordinates, or 4 if we wanted to discuss time, but that isn't important right now). This makes it clear that the surface of the balloon doesn't have an extra "third" coordinate, but it comes at a price. There's no way to cover the whole sphere in a single coordinate system, since by definition if 
and 
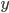are both real numbers, you get a plane, not a sphere. And even if we say 
and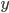 
are only allowed to take certain values, you just get a subset of a plane, like for example a disk or a strip. And no piece of a plane is shaped like a sphere.
(Sensible physicists would probably use spherical coordinates, but these have the issue that multiple coordinate locations refer to the same point.)
So what people do instead is try to cover the spacetime with multiple patches. In the case of a sphere, you can cover it with two patches, e.g. you could cover the surface of the Earth with two disks: one whose center is the "north pole" and wraps the sphere down to just below the equator, and the other a disk whose center is the "south pole" and wraps the sphere to just above the equator. Then we can put one coordinate system (a "chart") on each patch. The two patches overlap a bit, in order to prevent ourselves from getting confused as we travel from one coordinate system to the other. And to make sure we can do calculus on the sphere, we have to check that in the place where the two charts overlap, we can differentiate functions an arbitrary number of times, and that the results agree on both charts. See Atlas and Manifold for more details, if you dare.
But all of this is obscure and silly technicalities which are only really important if you need to do a calculation using coordinates, or want to define the notion of a "spacetime" in the most general way possible. Really the point has nothing whatsoever to do with the expansion of the universe, just the difficulty in laying down coordinate systems on spheres. Stick with the balloon and galaxies, I promise you they are more physically illuminating.
Also, I notice that the videos have a few errors and misconceptions in them:
* A historical error is that St. Lemaitre proposed (what was later called) the Big Bang theory out of religious motivations in order to support his account of Creation. In fact he discouraged Pope St. Pius XII from making such claims, because he didn't think one should mix theology and cosmology.
* A (related) theological error is that God "creating" the universe refers to something that only happened at the beginning of the universe, not something that is true for all times and places.
* Some of the physics is not well-explained either. The video contradicts itself when first it says that 1) nobody knows what happened at the beginning of the universe, and then it says 2) that time wasn't well-defined, so there was no time before, and then it says (3) there are some models where there was time before! Since (1) is true, we can't know for sure whether (2) or (3) or something else is true, and thus time may or may not have been well-defined, and it may or may not have been the beginning of time. I've discussed the evidence both ways as best I can in the series you are commenting on, but the bottom line is that nobody knows for sure.
Also I can see why the explanation of expansion and infinity would be confusing.
* The other video also has a physics error when it says that we can see things outside our Hubble volume because the expansion of the spacetime is accelerating. In fact we can see them because the Hubble constant (which measures the rate of expansion) was decreasing, which is the opposite.
Dr. Wall, I was hoping you could comment on some more topics I found concerning the singularity. Recently a chart was brought to my attention describing the four main competing theories for the Big Bang:
1. Inflationary cosmology proposed by Alan Guth in 1981, that at the singularity, gravity repelled instead of attracted. To my knowledge, this has been fairly confirmed by the cosmic microwave background measurements taken in March of last year. Also, some say this predicts a multiverse.
2. Loop Quantum Cosmology proposed by Bojowald and Ashtekar in 1999. Basically the oscillating universe theory rehashed, if I understand it correctly. I think thermodynamics of a closed system pretty well rules this one out.
3. String Gas Cosmology proposed by Robert Brandenberger in 1989. Nine dimensions of strings all scrunched up together until one string collides with an anti string and the whole mess unravels, aka the Big Bang. Three dimensions expand to the way we know them now, and the other six get compressed to infinitesimally unnoticeable size.
4. M-theory proposed by Edward Witten in 1995. I don't know how to describe this one, but I assume you're familiar with it to a far better degree than I. 2-D membranes exist, collide and make universes. Something like that.
Here's a link to the chart: http://mentalfloss.com/sites/default/files/reformatted-full-size.png
I don't know what kind of research exists as to the validity of these theories, especially the last two. But do any of these theories at all rule out the necessity for God as the cause of the universe?
Thanks!
Hi Nick,
I'm not a big fan of the chart you linked to because it compares some ideas which are at radically different stages of development as though they were parallel ideas. Specifically:
1. Inflationary cosmology is a very respectable model of the early stages of the universe, in which the universe exponentially grows. While it is not 100% proven, there's a decent amount of observational evidence, and most scientists believe it is very likely to be true. Most inflationary models predict that the universe is much bigger than the observable universe, and in that sense there would be other universes besides our own (though really they would just be different parts of our own universe). What inflation does NOT do by itself is remove the need for a beginning of some type, since the BGV theorem strongly suggests that inflation began with time. However, inflation tends to remove all evidence of what happened before inflation, making that time period even more mysterious.
2. Loop Quantum Cosmology is a hot topic among Loop Quantum Gravity people, but I don't think it's very promising. Since nobody understands the dynamics of LQG, it isn't really derived from LQG in a legit way. Instead they remove all but a small number of degrees of freedom (like the overall "size" of the universe) and then try to "quantize" that reduced theory using LQG-inspired methods. I doubt this gives a very accurate picture of a real cosmology with infinitely many degrees of freedom. And yes there are issues with the 2nd law if one tried to use this to avoid a beginning. (Unless there is a reversal of the arrow of time.)
3. String gas cosmology is an interesting model which I know only a little bit about. As far as I know it is one possible valid approach within string theory. There is no experimental evidence that string theory is correct, although it passes a number of consistency checks.
4. M-theory is just a name for what string theory really is, if only we understood it better. There are some indications that it involves membranes with 2 and 5 dimensions wiggling around in an 11 dimensional spacetime, but nobody really understands it except in certain limits where it reduces to different weakly interacting string theories.
As such, M-theory is not a name for an alternative Big Bang scenario and does not belong on the chart! Maybe there are some scenarios which avoid a Big Bang which use M-theory, but that's piling speculation on speculation. It looks like the person who made the chart thinks that the "ekpyrotic scenario" means the same thing as "M-theory". That's a bad use of terminology, since M-theory is presumably a very complicated theory, consistent with many possible cosmological scenarios.
Pingback: Did the Universe Have a Beginning? – Carroll vs Craig Review (Part 1) | Letters to Nature
Dr. Wall,
Thank you very much for this essay! It is just what I need in connection with a book I am writing on science and the Bible. The statement, "So no one really takes this theorem (the Hawking-Penrose theorem, 1970) very seriously anymore,” is particularly valuable. However, I see from Google Scholar that citations to it have been increasing over the past 3 years, reaching a maximum last year. Someone, at least, is taking it seriously – no one who is well-informed, I take it.
I have one more, possibly embarrassing question. In my field, papers that have not undergone peer review, such as your post, are regarded with skepticism (even more than those that have undergone peer review). I am dimly aware that things are not that simple in physics and cosmology. Nevertheless, can you point me to some peer-reviewed work making some of the points you make in your post?
Well, OK, I do have one more, admittedly even more stupid question. To one as ignorant as I, the Hawking-Penrose theorem seems like an abstruse way to say something simple and obvious. Am I right that the complexities arise in attempting to minimize the constraints under which the theorem holds true?
Best regards,
Walt
Walter,
When I said that no one takes the Hawking-Penrose theorem very seriously anymore, I meant that it is widely believed that the conditions of the theorem don't hold in the early universe (during inflation). I didn't mean it isn't an interesting mathematical result, which contributes to our knowledge of what can and can't happen in general relativity, or that that their paper didn't introduce useful new terminology or ideas. There are many reasons why it is still useful in certain contexts... It's a historically very important paper and there are many reasons it continues to be cited! But that's different from saying it proves there was really was an intitial singularity.
Until I mentioned my own (peer-reviewed) article, nothing I said in this post is the least bit controversial. If you want an online review of singularity theorems, here's one by an expert here. But you should really get the book by Hawking and St. Ellis; it's the standard reference textbook for this area (alongside Wald's Gravity).
I assume that your book is primarily about other things, seeing as you are not an expert in this field?
Presumably the correct answer to this question involves disabusing you of the idea that the result is obvious, but I don't see how I could possibly do that until you first tell me why you think it is obvious.
*st Ellis :)
[Oops, nice catch. Fixed--AW]
Aron,
Thank you very much for the reference to Ford and to Hawking and St. Ellis, and thank you again for the present article.
I believe that I now understand enough of why the result is not obvious to make it unnecessary to explain why I initially thought that it was – thanks for offering to enlighten me. And I apologize for the unintended slur on the citability of your work.
My book proposes an empirical test of the truth of the Bible and is predicated on two assumptions, both of which are debatable; but if one does accept the assumptions, one has to accept the test.
1. There is an absolute truth that is independent of mankind's efforts to know it.
2. Science is making progress towards discovering that truth; i. e., we know more now than we did millennia ago and continue to know more and more as time passes.
Then a decrease in the number of conflicts between a religion and scientific belief over time is evidence for the truth of the religion, and an increase in the number of conflicts between a religion and scientific belief is evidence against the truth of the religion. For this approach, the total number of conflicts is immaterial: all that matters is the trend, or the changes in the number of conflicts over time. So I am going through the history of science, plotting the cumulative changes in scientific belief over time and assigning positive and negative values according to whether the change brings science and the Judeo-Christian Bible closer together or further apart. The idea that the universe may have had a beginning is one point (of convergence) on the plot. I am trying to get the representation of that idea and its present status as nearly correct as I can.
Huseyn Qurbanov is permanently BANNED for posting incomprehensible Google-translated text, previously posted to other blogs, in violation of rule 9. This is the second offense with the exact same text.
Pingback: BİLİM DOSYASI : Büyük Patlama Teorisi’ne Dair 10 Soru, 10 Cevap ! | İstihbarat
Pingback: Büyük Patlama Kuramı’na İlişkin 10 Soru-10 Yanıt! – Prof. Dr. Ahmet SALTIK
Theorems in physics tell us nothing about nature. They only tell us what to expect given the supposed "truth" of certain facts, laws, and/or theories in physics. Thus, theorems cannot legitimately be used as evidence for a beginning of the universe. Only empirical evidence can give us information on the nature of the universe.
Do you think anything from this theorem by John Manchak provides a reason to be skeptical about whether any of the theorems used to support a beginning apply to our universe?
[Link was invalid, see below---AW]
New link:
"Can we know the global structure of spacetime?" by John Byron Manchak.
https://www.sciencedirect.com/science/article/abs/pii/S1355219808000580