Suppose you want to write down the laws of physics. How would you go about it?
What? You want to do some experiments first? Forget about that. This is theoretical physics. Let's not worry about pedantic things like what the actually correct laws of physics are. Instead, let's try to ask what they should look like more generally. What are the ground rules for trying to construct laws of physics?
(Of course, in reality we do get these ground rules from experiment. The way it works is, we make up rules to describe lots of specific systems which we actually measure, and then eventually we get some idea of what the meta-rules are, i.e. the rules for constructing the rules. But let's just try to make something up here, and see how close we get to reality.)
Let's try to do this step by step. Let's take for granted the existence of a spacetime. In the first step, we need to decide what kind of entites there are moving around in this spacetime. Since we're on the hook for giving an exact description, we'd better start with something which is mathematically simple. For example, we could postulate that there are a bunch of point particles flying around. If there are 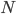 particles, and space is 3 dimensional, then we can describe all of their positions with
particles, and space is 3 dimensional, then we can describe all of their positions with 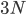 parameters. (We can then think of the universe as a point moving around in a
parameters. (We can then think of the universe as a point moving around in a 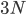 dimensional space, called configuration space.)
dimensional space, called configuration space.)
Or maybe there's a bunch of strings wiggling around. Or perhaps there are fields, whose values are defined at each point of space. (In these cases, we will need an infinite number of parameters to describe what is going on at each moment of time! But don't worry—since we won't be doing any actual calculations, this won't necessarily make things any harder.)
All right. Now that we've decided what kind of stuff we have, we need to know how it changes with time. For this we need to write down equations of motion.
We could write down an equation involving one derivative of positions with respect to time. This would determine the velocity of each piece of particle/string/field/whatever in terms of its position. But that won't be like real physics since real physical objects have inertia. Stuff keeps on trucking until a force acts on it. This means that the future motion of an object doesn't just depend on where it is right now, but also on how fast it is going.
So instead we need to write down an equation involving two derivatives of the position with respect to time. This will determine the acceleration of each entity, as a function of its position and/or velocity. That's a bit more like real life. (In other words, to work out what happens we need to know about both the positions and velocities. If we have 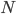 particles, this is a
particles, this is a 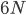 dimensional space called phase space.)
dimensional space called phase space.)
So you could just sit down and write down some second-order differential equation equation involving acceleration, and call that the laws of physics. But most of these would still be qualitatively different from the fundamental laws of actual physics. For example, nothing would stop you from including friction terms which would cause the motion of objects to slow down as time passes. For example, if we have a particle moving along the x-axis, we could write down an equation like this:
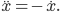
So physics has more rules then one might think are really necessary. You can't just write down any old equations of motion. They have to be special, magical equations, which satisfy certain properties.
We could just make some giant list of desired laws. But that would be rather ad hoc. Instead, physicists try to derive all of the magic from some simple framework. We've just seen that just writing down equations of motion is not the best framework since it doesn't guarantee basic physics principles like conservation laws.
There are two particularly simple frameworks which can be used. For most systems these are equivalent, and you can derive one framework from the other. I'm just going to summarize these at lightening speed here:
- Lagrangian mechanics: Here the fundamental concept is the action, a number
obtained by integrating some function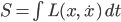
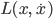 of the positions and velocities over all moments of time. (
of the positions and velocities over all moments of time. (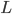 is called the "Lagrangian", and is normally equal to the kinetic energy minus the potential energy). The basic rule is that a small change
is called the "Lagrangian", and is normally equal to the kinetic energy minus the potential energy). The basic rule is that a small change 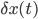 in the paths of particles/strings/fields/whatever in any finite time interval
in the paths of particles/strings/fields/whatever in any finite time interval 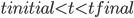 should leave the action unchanged, to first order (i.e. up to terms linear in
should leave the action unchanged, to first order (i.e. up to terms linear in 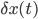 ). In other words:
). In other words:
Here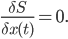
 can be any of the position parameters in the theory. Once you write down a single equation specifying
can be any of the position parameters in the theory. Once you write down a single equation specifying 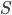 , all of the equations of motion for all entities are determined by this rule.
, all of the equations of motion for all entities are determined by this rule.
.
As a simple example, consider a point particle moving along a 1-dimensional coordinate , with a potential
, with a potential 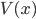 which depends on your position. This might describe a train sliding frictionlessly along a roller coaster track, where
which depends on your position. This might describe a train sliding frictionlessly along a roller coaster track, where  is the length measured along the track and
is the length measured along the track and 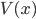 is proportional to its height measured from the ground. The Lagrangian is kinetic energy minus potential energy:
is proportional to its height measured from the ground. The Lagrangian is kinetic energy minus potential energy:
The rule here is that given the initial and final locations of the train in some short time interval, the train moves in a way that minimizes the total action of its trajectory—which implies by basic principles of calculus that small variations of the path have to leave the action unchanged.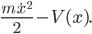
.
Imagine if you are walking from your house to a shop. You leave your house at 9 am, and you need to be at the shop at exactly 10 am. You don't like walking too quickly, because it expends too much energy. On the other hand, if it's a bit chilly you might also prefer to spend more time in sunny areas, and less time in shady areas. What would you do? If you want to maximize your happiness (or minimize your unhappiness), you would compromise by walking more quickly in the shade than in the sun. Similarly, if we fancifully suppose that the train had a soul and that it preferred to spend more time up high (so long as it gets to its destination on time), we would then have an explanation for why the train lingers at the higher parts of the track. More generally, when the potential energy is higher the kinetic energy is less—one can prove that the total energy is conserved.
- Hamiltonian mechanics: The fundamental concept here is that all parameters in physics come in ``conjugate'' pairs. For example, for a regular particle, the conjugate variable to the position
 is the momentum
is the momentum 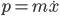 , while the conjugate variable to momentum is minus the position,
, while the conjugate variable to momentum is minus the position, 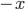 . (That minus sign is important: without it conservation laws wouldn't work properly.) The variable which is conjugate to time is known as the "Hamiltonian"
. (That minus sign is important: without it conservation laws wouldn't work properly.) The variable which is conjugate to time is known as the "Hamiltonian"  —this turns out to be nothing other than the total energy of the system (kinetic plus potential). It turns out that if you know the Hamiltonian
—this turns out to be nothing other than the total energy of the system (kinetic plus potential). It turns out that if you know the Hamiltonian 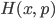 as a function of the positions and their conjugate momenta, you can work out everything that happens. You work out the equations of motion with the rule (called "Hamilton's equations" that the change of a parameter with respect to time, equals the change of the energy with respect to the conjugate variable. In other words:
as a function of the positions and their conjugate momenta, you can work out everything that happens. You work out the equations of motion with the rule (called "Hamilton's equations" that the change of a parameter with respect to time, equals the change of the energy with respect to the conjugate variable. In other words:
The minus sign in the second equation means that position is to momentum as momentum is to minus position, just like I told you.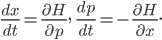
.
A consequence of "Hamilton's equations" is that, assuming does not depend on some particular position coordinate
does not depend on some particular position coordinate  ,
, 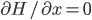 and so
and so 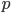 is conserved. More generally, Hamilton's second equation says that the "force"
is conserved. More generally, Hamilton's second equation says that the "force" 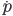 is zero when the gradient (i.e. derivative) of
is zero when the gradient (i.e. derivative) of  with respect to position is zero. Similarly, if the gradient of
with respect to position is zero. Similarly, if the gradient of  with respect to the
with respect to the 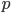 coordinate is zero, then
coordinate is zero, then 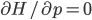 , and Hamilton's first equation says that the velocity
, and Hamilton's first equation says that the velocity 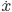 is zero. If the fomula for kinetic energy is the usual nonrelativistic formula
is zero. If the fomula for kinetic energy is the usual nonrelativistic formula 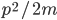 (written as a function of the momentum
(written as a function of the momentum 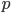 instead of
instead of 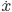 since this formulation of physics is all about
since this formulation of physics is all about 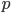 's), this tells us that the "velocity" is zero when the momentum is zero.
's), this tells us that the "velocity" is zero when the momentum is zero.
.
More generally, Hamilton's equations tell you that if you graph out the 2 dimensional phase space of a particular pair of x-p coordinates, the trajectory of the system in the x-p plane is at right angles to the direction of the gradient of , and equal in size to the gradient. This means that the system always moves along a direction where
, and equal in size to the gradient. This means that the system always moves along a direction where  isn't changing, and so
isn't changing, and so  is conserved (unless we make it an explicit function of time, in which case we would have to write it as
is conserved (unless we make it an explicit function of time, in which case we would have to write it as 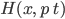 ).
).
From either of these two equivalent formulations of physics, there is a famous theorem first proved by Emmy Noether. She showed that any time  or
or 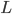 has a symmetry which shifts some parameter, its conjugate parameter is conserved (it doesn't change with time). I've already shown you some specific examples (symmetry with respect to
has a symmetry which shifts some parameter, its conjugate parameter is conserved (it doesn't change with time). I've already shown you some specific examples (symmetry with respect to  shifts makes
shifts makes 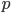 be conserved, symmetry with respect to
be conserved, symmetry with respect to 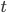 shifts makes
shifts makes  be conserved). This is the most important theorem in all of theoretical physics.
be conserved). This is the most important theorem in all of theoretical physics.
If you just start by trying to write down equations of motion for your laws of physics, you can't prove Noether's theorem. It just doesn't work. Since you don't have a notion of conjugate quantities, you can't even get started. Many important physical concepts such as energy, momentum, mass, force, and so on won't even be defined. So there's a lot more to life than the equations of motion.

Thanks for sharing this very exciting knowledge. I will definitely try this for constructing laws.
Hi Aron. What a great essay! Hey, one minor typo in the above though... In reference to Hamilton's equations, you said,
Unless I'm missing something, I think you meant to say that position is to momentum as momentum is to minus position. :-)
Hope this finds you, Nicole, and Samuel well.