In my last post about spacetime, I explained how the geometry of spacetime is determined at each spacetime point by a set of 10 numbers. These 10 numbers are packaged together into a  matrix called the metric, which is written as
matrix called the metric, which is written as 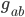 . The subscripts
. The subscripts 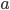 and
and 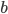 stand in for any of the 4 coordinate directions (in a 4-dimensional spacetime). Since the metric is symmetric, i.e.
stand in for any of the 4 coordinate directions (in a 4-dimensional spacetime). Since the metric is symmetric, i.e. 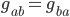 , there are 10 possible numbers in this matrix. The value of these 10 numbers depends on your position and time,which makes them a field, specifically the gravitational field.
, there are 10 possible numbers in this matrix. The value of these 10 numbers depends on your position and time,which makes them a field, specifically the gravitational field.
However, there is an important caveat in all this. The coordinates which you use to describe a given spacetime are totally arbitrary. For example, a flat 2-dimensional Euclidean plane can be described using Cartesian coordinates 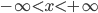 and
and 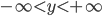 . In this coordinate system, the distance-squared is given by the Pythagorean formula
. In this coordinate system, the distance-squared is given by the Pythagorean formula
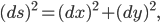
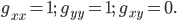
On the other hand, for applications involving rotations, it's often useful to use polar coordinates: 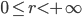 (the distance from the origin) and
(the distance from the origin) and 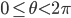 (the angle around the origin, measured in radians). They're related to the original coordinate system by
(the angle around the origin, measured in radians). They're related to the original coordinate system by
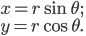
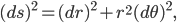
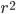 factor comes in because circles that are a greater distance from the origin have a larger circumference, so there's more space as you move outwards. This can be written in terms of the metric like this:
factor comes in because circles that are a greater distance from the origin have a larger circumference, so there's more space as you move outwards. This can be written in terms of the metric like this: 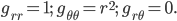
(Note: I've given these coordinate systems their traditional coordinate names to make them look more familiar, but this is actually just a redundancy to make it easier for humans to think about it. I could have written the two coordinates as 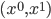 —the superscript being a coordinate index, not an exponent—and then you could tell whether it was Cartesian or polar coordinates just by inspecting the formula for the metric.)
—the superscript being a coordinate index, not an exponent—and then you could tell whether it was Cartesian or polar coordinates just by inspecting the formula for the metric.)
Now the point is, these two coordinate systems describe the same geometry in a different coordinate system. If we were playing pool (or billiards) on a planar surface, and you wanted to describe how billiard balls bounce off of each other, you could equally well describe it using either coordinate system. The physics would be the same.
Of course, the language you use to describe the system differs. Suppose that I analyze a collision using Cartesian coordinates, while you use polar coordinates. And suppose we had to communicate to each other what happened. If you say to me, "The cue ball had a velocity in the 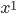 direction", then I'll get confused because
direction", then I'll get confused because 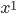 means something different to me than it does to you. These kind of statements vary under a change of coordinate system, they are "relative" to your coordinate-perspective. So if you want to communicate with me, you have to find a way to describe what's going on which does not refer to coordinates in any way. For example, you could say "The cue ball hit the 3 ball, which knocked the 8 ball into a pocket." Since the two balls and the pocket are unique physical objects, we can all agree on whether or not this happened, no matter what coordinate system we use. These kind of statements are invariant under a change of coordinate system. The goal of coordinate-invariant physics is to describe everything in this sort of way.
means something different to me than it does to you. These kind of statements vary under a change of coordinate system, they are "relative" to your coordinate-perspective. So if you want to communicate with me, you have to find a way to describe what's going on which does not refer to coordinates in any way. For example, you could say "The cue ball hit the 3 ball, which knocked the 8 ball into a pocket." Since the two balls and the pocket are unique physical objects, we can all agree on whether or not this happened, no matter what coordinate system we use. These kind of statements are invariant under a change of coordinate system. The goal of coordinate-invariant physics is to describe everything in this sort of way.
Here's another way in which coordinate systems can let you down: when you use polar coordinates, there are places where the coordinates go kind of funny. For example, when you're going around the origin clockwise in the direction of increasing 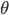 , and you arrive at
, and you arrive at 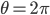 , you immediately teleport back to
, you immediately teleport back to 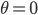 since you've come full circle. Even stranger, space seems to come to an end at
since you've come full circle. Even stranger, space seems to come to an end at 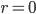 (the origin) since there's no such thing as negative
(the origin) since there's no such thing as negative 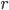 . And if you're sitting right at
. And if you're sitting right at 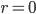 , the different values of
, the different values of 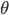 all refer to the same point as each other. However, in reality we know that nothing weird is happening to the geometry at any of these points, since nothing strange happens in Cartesian coordinates. (A similar issue comes up in black hole physics. The original set of coordinates found by Schwarzschild blow up at the event horizon, but actually nothing unusual happens there in classical general relativity.)
all refer to the same point as each other. However, in reality we know that nothing weird is happening to the geometry at any of these points, since nothing strange happens in Cartesian coordinates. (A similar issue comes up in black hole physics. The original set of coordinates found by Schwarzschild blow up at the event horizon, but actually nothing unusual happens there in classical general relativity.)
The upshot of all this for general relativity is the following: I told you above that you can describe general relativity using the metric 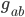 , which involves 10 numbers at each point. But this description actually has some redundancy in it, since there's infinitely many possible coordinates systems you could use (one for each way of labelling the points uniquely with four numbers), and the metric looks different in each one—it isn't an invariant object.
, which involves 10 numbers at each point. But this description actually has some redundancy in it, since there's infinitely many possible coordinates systems you could use (one for each way of labelling the points uniquely with four numbers), and the metric looks different in each one—it isn't an invariant object.
When a theory has redundancy like this, we say there is a gauge symmetry. A regular symmetry says that two different states (i.e. configurations) of a system behave in the exact same way as each other. A gauge symmetry is stronger than a regular symmetry: it says that the two configurations are actually the same physical state of affairs. In general relativity, the choice of coordinates is a gauge-symmetry. It is a mere human convention which doesn't correspond to any actual physical thing in Nature.
Of course, even if you aren't doing general relativity, you can still use whatever coordinate system you like! Most games of billiards can be understood in the approximation where space is flat (unless you like to spice up your games with black holes and gravity waves, like the cool kids do!) In flat space time, all coordinates are equal, but some are more equal than others. Although nothing stops you from calculating in horrible coordinates, the laws of physics look especially simple in ordinary Minkowski coordinates, where the symmetries of spacetime look especially simple. Since Newton's First Law of motion holds in these coordinates, we call it an inertial frame. (Here I'm ignoring the downward pull of gravity, since in billards we're only interested in horizontal motions.)
However, if you're doing general relativity, then there's a property of spacetime which forces you to describe physics in a coordinate-invariant way; at least if you want the equations of the theory to look elegant and lovely instead of like horrendous cludge. This property is called curvature—but we're out of time for today.
