The Ten Symmetries of Spacetime

Previously, I described the main formula of Special Relativity:

$$s^2 = (\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (\Delta t)^2.$$

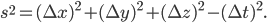
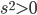This formula tells us the amount of distance squared between two points (if $s^2 > 0$) or the amount of duration squared (if 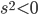$s^2 < 0$).  (By using some trigonometry we can also use this formula to figure out the size of angles, so this encodes everything about the geometry).  All the crazy time dilation and distance contraction effects you've probably heard about are encoded in this formula.

Today I want to talk about the symmetries of spacetime.  What I mean by a symmetry is this: a way to change the coordinates 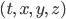$(t,\,x,\,y,\,z)$ of spacetime in a way that leaves the laws of physics the same.  Now I haven't told you what the laws of physics are, but the important thing is that they depend on the geometry of spacetime.  So that means that we need to check in what ways we can change the coordinates of spacetime without changing the formula for $s^2$.

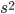The first kind of symmetry is called a translation.  This consists of simply shifting the coordinate system e.g. one meter to the right, or one second to the future.  This doesn't affect the formula for 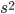$s^2$ since it only depends on the coordinate differences 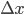$\Delta t$, $\Delta x$ etc.  We can write a time translation like this:

$$t^\prime = t + a,$$

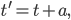
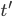i.e. the new time parameter $t^\prime$ equals the old one plus some number 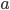$a$.  Similarly, the three possible kinds of spatial translations are: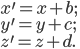

$$x^\prime = x + b; \\ y^\prime = y + c; \\ z^\prime = z + d.$$

By choosing the numbers a, b, c, d, arbitrarily, one obtains a four dimensional space of possible translation symmetries.

The second kind of symmetry is more complicated, but you've certainly heard of it before—it's called a rotation.  If we have two spatial coordinates, then we can rotate them by some angle 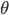$\theta$ (measured in radians), which leaves all the distances the same.  The algebraic formula for a rotation looks like this:

$$x^\prime = \phantom{-}\cos (\theta) \, x + \sin (\theta) \,y; \\ y^\prime = -\sin (\theta) \,x + \cos (\theta) \,y.$$

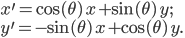
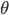That involves some trigonometry, but things look a bit simpler if we take the angle $\theta$ to be a really tiny parameter 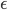$\epsilon$, and just consider the resulting infinitesimal coordinate changes $\delta x \approx (x^\prime - x)$:

$$\delta x = \phantom{-}\epsilon\,y; \\ \delta y = -\epsilon\,x.$$

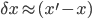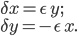
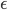Translated into English, that says that if you rotate the y-axis of your coordinate chart a little bit towards the x-axis, you have to rotate the x-axis a little bit away from the y-axis (or vice versa if $\epsilon$ is negative).  I'm too lazy to draw this, but if for some reason you can't visualize it, a little bit of fidgeting with any rigid flat object should convince you.

Now actually we have three different spatial coordinates: x, y, and z.  That means that you can actually rotate in 3 different ways: along the x-y plane, the y-z plane, and the z-x plane.  Of course there are other angles you can rotate at as well, but they are all just combinations of those three; in other words the space of possible rotations is 3-dimensional.

But now, what about the time direction?  It would feel terribly lonely if it were left out, and in fact it is also possible to rotate spacetime about the t-x plane, the t-y plane, and the t-z plane.  However, remember how time is not quite the same as space?  Instead, it's just like space except for a funny minus sign.  So not surprisingly, the formula for a rotation also has a funny minus sign—or rather, a funny absence of a minus sign:

$$\delta t = \epsilon\,x; \\ \delta x = \epsilon\,t.$$

So if you rotate the t-axis towards the x-axis (which corresponds to changing your coordinate system so that you are travelling at a constant speed), then the x-axis has to rotate towards the t-axis (which means that your notion of simultaneity has to change as well).  If you know how to integrate this with calculus, you can get the effects of a finite "rotation" in space (called a Lorentz boost) through an "angle" $\chi$:

$$t^\prime = \cosh (\chi) \, t + \sinh (\chi) \,x; \\ x^\prime = \sinh (\chi) \, t + \cosh (\chi) \,x.$$

In the above, cosh and sinh are functions similar to cosine and sine but defined using hyperbolas instead of circles.

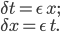
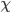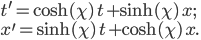
So this rotation has some wierd properties: It describes a crazy world (ours!) in which things rotate in hyperbolas instead of circles.  That's because of the minus sign in the formula for 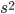$s^2$ above, which makes it so the points of equal distance (or duration) correspond to hyperbolas instead of circles.  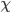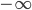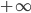This has some additional consequences: 1) Because hyperbolas are infinitely long, the "hyperbolic angle" $\chi$ ranges from $-\infty$ to $+\infty$, unlike circular angles which come back to where you started after you rotate through 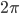$2\pi$ radians.  2) Because the two axes both move towards (or both move away) from each other, when you do a really big rotation it scrunches everything up towards 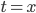$t = x$ or $t = -x$.  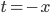What this means is that when you accelerate objects more and more, they don't go arbitrarily fast.  Instead they just get closer and closer to the speed of light.

In conclusion, spacetime has 10 kinds of symmetry: 4 kinds of translations and 6 kinds of rotations.  The space of possible symmetries is 10 dimensional.  It is called the Poincaré group.

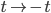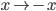P.S. In this whole discussion I have ignored the possibility of reflection symmetries such as $t \to -t$ or $x \to -x$.  These are also symmetries of the formula for 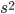$s^2$, but they are discrete rather than continuous—there's no such thing as a "small" reflection the way you can have a small rotation.  Adding these in doesn't change the fact that the Poincare group is 10 dimensional.  However, these transformations are actually NOT symmetries of Nature.  They are violated by our theory of the weak force.  The only discrete symmetry like this which is preserved by the weak force is CPT: the combination of time reflection, space reflection, and switching matter and antimatter.