A reader asks:
This seems to be as good a place as any to ask a question about closed universes.
See, in a lot of popular science books, they teach you that an "open" universe is one where space is infinite, saddle-shaped, and keeps expanding forever; a "flat" universe is infinite, plane-shaped, and the rate of expansion eventually peters out to zero; and a "closed" universe is finite, sphere-shaped, and eventually contracts in a big crunch. They then talk about the cosmological constant and "dark energy," which make our universe expand at an accelerating rate, something that doesn't fit the taxonomy of possibilities for the universe's topology, and which they do not relate back to that taxonomy in any way.
Can a universe with lots of dark energy be a closed universe? Will a closed universe with dark energy keep on expanding and accelerating, or will it eventually collapse in a big crunch like a "normal" closed universe? Is the three-type Taxonomy only relevant given certain energy conditions? (Strong/weak/null)
Oh, and I almost forgot:
are there any good reasons to think that the universe is closed in the first place, other than Kalam-esqe arguments against actual infinities?
David,
It sounds like these books were just adding the new material about the cosmological constant to the old discussions without doing the hard work of going back and revising it so that it makes sense.
The Bad Old Days
In the old days (pre circa 1998) people didn't know about the acceleration of the universe, and they thought that the universe just consisted of ordinary radiation and matter (where for these purposes, dark matter is a form of matter). In the old days, the model of closed, flat, and open works exactly as you say: a closed universe (spherical geometry) will recollapse, and open one (hyperbolic geometry) will trend to a constant rate of expansion (in terms of distance / time) and a flat one is right on the edge and will expand forever at a slower and slower rate (but still getting arbitrarily large).
Given the rate of expansion, it takes a certain amount of energy density to get a flat universe. Too much, and you get a sphere, too little and you get hyperbolic space. (The expansion or contraction of the universe makes it hyperbolic in the absence of matter.) These are the 3 kinds of geometries which are homogeneous (the same everywhere) and isotropic (the same in every direction). On average, the observable universe seems to be homogenous and isotropic, so it's got to be one of these three (a.k.a. an "FRW cosmology").
However, this was confusing for several reasons. One is that the cosmological data kept suggesting that there wasn't enough energy in matter to get anywhere close to a flat universe, yet other data seemed more consistent with a flat universe. A flat universe is also a natural consequence of inflation since it stretches out the pre-existing geometry to exponentially large distance scales. Also, the universe seemed like it wasn't quite old enough to explain all the structures in it.
Concordance Cosmology
Now we know that there is an additional form of energy which is confusingly called "dark energy" (but I dislike this name, because it makes people think it has something to do with "dark matter".) Most likely it is just a cosmological constant, a constant energy density in all of space.
Now it turns out that for purposes of determining the spatial geometry, a positive cosmological constant counts positively (so it helps to close the universe). But when you calculate its effect on the expansion of the universe, it counts negatively, as repulsive gravity.
This may seem like odd behavior because energy and mass are equivalent, and we all know that mass causes gravitational attraction, not repulsion. But in turns out that in General Relativity, both energy density (associated with time) and pressure (associated with space) lead to attractive gravity. Negative pressure is called tension, and tension therefore causes antigravity.
In ordinary matter travelling at low speeds, the amount of pressure/tension is typically very small compared to the energy density. Radiation which travels near the speed of light has a lot of pressure, but that only makes gravity stronger.
On the other hand, a positive cosmological constant has tension equal to its energy density. Something has tension if, when you stretch it out, it's energy increases. But the energy of the cosmological constant is proportional to the volume, so when the volume increases the energy increases proportionally. Hence the tension in each spatial direction is equal to the energy. Since there are 3 dimensions of space and only 1 of time, the antigravity due to the tension is 3 times larger than the gravity due to the energy density. Hence the antigravity wins! So paradoxically, the gravitational effects of this tension just make the universe want to grow faster! Unlike the usual effects of tension, which cause things to shrink in on themselves.
On the other hand, if the cosmological constant were negative (it isn't, but suppose) its effects would be reversed: it would make the spatial geometry more hyperbolic, but would decelerate the expansion.
So, once you include a cosmological constant, the rules change (as you guessed). You can still have the same 3 types of spatial geometry (the words "open", "flat", and "closed" describe the spatial geometry, not the dynamics). But with a positive cosmological constant, even a universe with closed topology can sometimes expand forever, if it gets big enough for the cosmological constant to take over. (Matter thins out, while the CC doesn't, so when the universe is small the matter is more important, and when it gets larger the CC is more important.) On the other hand, with a negative cosmological constant, even an open cosmology will always eventually recollapse when it gets big enough.
(The various energy conditions you mention place limits on the allowed energy density and/or tension/pressure, so not surprisingly these have certain implications for what a cosmology can do. Note that a positive CC violates the strong energy condition—which allows for a bounce, at least in the case of a closed universe. While a negative CC violates the weak energy condition, which requires that any FRW cosmology which is neither expanding nor contracting at some time, must be closed. (OK, technically it also allows space to be flat, but only if the matter energy is exactly 0, which is unrealistic.))
Our universe seems to have a positive cosmological constant, which fixes all of the problems I mentioned above. The cosmological constant seems to give us exactly the extra energy density we need to get a flat universe. Yet it also causes the universe to be currently accelerating in its expansion (lengthening the projected time back to the Big Bang); this acceleration has been confirmed by surveys of supernovae in the past. So everything seems to hang together consistently.
As far as we can tell from current observation, the universe is exactly flat (with experimental error of about 1-2% over scales comparable to the observable universe) However, a flat geometry is right on the knife's edge between the spherical and hyperbolic cases, so actually this is perfectly compatible with the universe having a tiny positive or negative curvature, as long as the radius of curvature is big enough.
So really it could still be any of the three cases, or else something more irregular. As I said, inflation blows up the size of the universe, so regardless of the initial geometry, the observable universe will look flat after enough inflation. Outside the observable universe, for all we know, it could be some other shape, perhaps it isn't even symmetrical.
There is really no particularly good physics reason, apart from aesthetics and philosophical bias to think that the universe should be closed or open. I personally don't think much of the "Kalam" argument that actual infinities are impossible, but I do find it distasteful that in an infinite homogeneous universe everything (including all possible histories of the Earth) would happen infinitely many times in different places.
Also on the speculative hypothesis that the universe originated from some kind of quantum fluctuation, or no-boundary condition, I think one expects it to be closed. But this kind of thing is extremely speculative.
If I had to place a bet with a metaphysical bookie, my money would be on closed (but enormously large so that we could never tell). But this is my own personal guess, not a conclusion of Science!
(Incidentally, even if the topology of space is flat or hyperbolic, it would still be possible for the universe to be finite in size and therefore closed, so long as it has nontrivial topology. For example, space could be a really big "torus" where if you go far enough in one direction, you come back around on the other side, like in some video games. Locally, such a universe couldn't be distinguished from the infinite case, but globally it would be different. Astronomers have done measurements looking for nontrivial topology in the sky. They haven't seen anything, but of course they wouldn't if it happened on a scale much bigger than the observable universe!)
On the other hand, if the universe really does have a positive cosmological constant than (regardless of its spatial geometry) the final outcome seems secure. If we extrapolate the current laws of physics to the far future (assuming no changes or interventions), we get an exponentially growing universe. The matter thins out and becomes unimportant, and you end up with a very tiny final temperature (corresponding to the analogue of Hawking temperature but for cosmological horizons instead of black hole event horizons).
William Lane Craig and Quentin Smith covered this kind of debate pre-discovery of the cosmological constant, really well in the book "Theism, Atehism and Big Bang Cosmology" Craig actually defended the Open Universe using using Allan Sandages argument, in order to refute Gott-Li's CTC but their discussion is outdated. (Still interesting though!)
Hey Dr. Wall,
This was once again a very enlightening post, which is outside of my field of expertise. However, in my philosophical studies I've come to see the Kalam as a good argument (It seems that the premises are true and therefore the conclusion follows from plausibly true premises). You state that you don't think much of the KCA, and I would like to find out which premise do you think is unlikely true? Or maybe I'm misinterpreting your statement. I do remember reading in an older post (in paraphrase form) that you believe people's beliefs should not be hanging from arguments. I agree! But nevertheless, this has nothing to do with whether the argument is a good one or not. So my question is, (if I'm understanding you correctly) why don't you think much of the Kalam?
Thanks.
John-Michael,
My questioner mentioned specifically "Kalam-esqe arguments against actual infinities", which I am given to understand were made by some medieval Islamic philosophers as part of a cosmological argument. In other words, I don't think there are any good purely Logical/Metaphysical reasons to reject a timestream which goes back in time forever. (As opposed to the various Physics reasons I discussed in my series on that topic.) I have clarified the post to make this clear.
I was not referring to the version of the "Kalam" argument advocated by St. Craig, which states as a premise that the universe had a beginning. (St. Craig sometimes makes philosophical arguments that actual infinities are impossible, but he also gets support from this premise via Modern Cosmology and so on.)
I agree with you that both premises of the Kalam Argument are plausibly true, and therefore it provides some evidence that God exists. However (as I have said in earlier posts) I don't consider it to be as compelling as other forms of the Cosmological Argument. The premises do not seem particularly secure.
I would never say that people's beliefs shouldn't depend on the validity of "arguments". It seems like any reason to believe in God (even a direct personal revelation) could be phrased in the form of an argument. What I do claim is that there are better reasons to believe in Christianity than abstract arguments from Physics or Metaphysics (even though I do think these arguments have some significant force!)
Thank you very much, Doctor Wall!
Just one more question on this particular subject.
Was the inflation field a kind of cosmological constant?
David,
Inflation is thought to be due to a scalar field/particle yet to be identified that has come to be known as the inflaton. It is not a cosmological constant, but its properties are such that it behaves like one when it's in an excited state. This behavior ceases when it "rolls down" or tunnels to a lower energy state (a process known as reheating) and inflation comes to an end. Back in the early 80's when inflation was first proposed it was thought that the Higgs boson might be the inflaton, but for a variety of reasons that didn't work out. Today we know almost nothing about it other than that it's composed of one or more scalar fields. We aren't even sure it exists (although most physicist are inclined to think it does). This is largely why there are almost as many inflationary cosmological models as there are cosmologists! :-)
Scott Church ,
Your answer to David raises some interesting questions. (1) What happens to inflaton
when it is done with rolling down? Could it become something which we see today as CC or it generates particles like quarks etc eventually?
(2) Can CC also be replaced by a scalar field or Einstein's equations will have problem in accommodating a scalar field?
"There is really no particularly good physics reason, apart from aesthetics and philosophical bias to think that the universe should be closed or open."
What about Olbers' paradox? Doesn't it rule out an infinite universe?
Kashyap,
(1) When the inflaton leaves its excited state (via rolling down or tunneling) it's cosmological constant-like behavior ends and so does inflation. At that point it would be just another scalar field with a broken symmetry like the Higgs. How that broken symmetry would manifest itself today (e.g. generating particles or the like) depends on what it turns out to be. As of this writing we have no idea, but it would no longer behave like a cosmological constant.
(2) As a matter of fact, there is such a theory. Some have postulated that there may be a background dark energy other than the cosmological constant which has come to be known as quintessence. I am familiar enough with the theory to know that it does have strengths and weaknesses, but I'm sure Aron could speak to that better than I.
Mactoul,
Actually, Olber's Paradox only rules out past-eternal (or very old) static universes, infinite or otherwise. Expanding universes with suitably large Hubble constants (like ours), or very young static ones are allowed.
Inflationary models usually involve a scalar field with a potential energy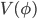
that is some function of the value of the field 
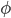. Whereas the CC is just a constant energy density not depending on a field.
By local energy conservation, the inflaton would have to turn into some other kind of energy as it rolls down its potential. It is natural to suppose it turned into the Standard Model fields (or fields that eventually turned into them...), since any matter which pre-existed inflation would have been diluted to near empty space. This period is called "reheating".
Quintessence (a scalar field instead of a late time CC) is a logical possibility, but it has some difficulties. It does not really explain the smallness of the cosmological constant, and in fact the scalar field requires additional fine tuning to make it have very small mass. It needs a small mass or it would have already rolled down its potential. (The mass squared is by definition just the piece of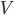
which is quadratic in 
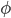, expanding around the minimum energy value.) Also, a quintessence field would allow for the tension of the dark energy to be different from the energy density, yet current measurments are consistent with the value being exactly equal ("w = -1"). Thus Occam's razor suggests it's just a CC. But it could be something more complicated.
Yeah, in an expanding infinite universe, Olber's paradox doesn't apply since the light from distant stars would be redshifted, and if far enough away, there would not be time since the Big Bang for the light rays to reach us.
(This raises another deep philosophical question, whether it is reasonable for there to exist different parts of the universe that have never had a chance to interact with each other. If they don't have a common origin, then what makes them similar?)
The argument used from the Kalam is that we could never get to the present if the past was infinite. Therefore the past must be finite in length. This argument has been made by Craig to support the Kalam, can you explain why you find it unconvincing?
howie,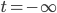
is not a time, rather it is the limit of a sequence of arbitrarily early times. There are (not necessarily) any actual "objects" or "things" existing at 
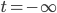, rather things exist at finite values of time. So I would answer the objection you raise by saying that no actual entities ever existed which would still need to "traverse" an infinite amount of time. (Just as objects can exist at arbitrarily late moments, in the other time direction.) No two actually existing times differ by a infinite amount of duration. Does that make sense?
Who is "we" in that argument?
That being said, there is something a little unsatisfactory about a timestream which extends infinitely far back to the past, insofar as it might leave some facts about the physical universe without any kind of explanation besides that they "always were that way". I personally think models that begin with a finite past are more elegant. But lack of elegance is not the same thing as logical impossibility.
Yes I think that makes sense. So to sum up , the logical argument for an impossibility of an actually infinite past is invalid, as an actually infinite past is not logically impossible. However the Kalam argument might still be valid if the universe happens to have a beginning, but that needs to be determined by the correct physical model, is that a correct summation? Thanks for the reply.
howie,
Yeah, that's pretty much what I think.
Aron,
I'm a little confused with the t=−∞ and you said that things don't exist at that limit. Rather, things exist at a finite value of time.
If this is the case, I'm wondering if we should even consider 'time' before the first thing appeared time at all? What would make it 'time' unless it's some sort of metaphysical time that does not relate to the physical world in any way?
And I'm wondering if you could clear up some confusions for me. If the Big Bang Theory is true and we use GR equation to rewind and predict the past, does it say that the all of space and time and energy were contained in the singularity? Or is it that at t=0 there was literally nothing, not even a singularity? And what is "in" the singularity when it was a singularity? I watched an episode of PBS Spacetime and it said that at t=1x10-^42 secs, all the law of physic breaks down. If this is the case, wouldn't this be the limit of our scientific inquiries since science is dependent on model we can produce with clearly defined axiom?
Again, thanks for your blog, I've learned a lot from just lurking here.
Dear Professor Wall,
Thank you for taking the time answer all my previous questions. I had aquestion on this matter that is of a more theological bent, since you did mention that you found the idea of an infinite universe distasteful, but not physically excluded, and I believe on your fine tuning lecture slides you stated a belief that both a multiverse and God were compatible in your view (to be clear, I am aware that multiverses such as the proposed string landscape and the infinite homogenous universe discussed herein aren't actually referring to identical concepts). Do you believe that God could have so chosen to create an infinite universe as discussed here for God's own reasons and still have considered it a good creation, or do you think that theism and an infinite universe are metaphysically incompatible? I have read articles by Professors Ellis and Mann regarding this matter that they believe that an infinite universe would be a serious philosophical issue for theism (though of course it isn't really experimentally provable), but I have also read articles by theists who seem to regard an infinite universe as no real problem to God's creativity and goodness.
Also, sorry if this comes off as somewhat spammy, but Merry Christmas!