I've written a pop-article about Time Machines and Event Horizons, which has appeared on the Scientific American blog Critical Opalescence. George Musser, my host, is an editor at Scientific American, and kindly gave me this opportunity to talk about some of my ideas in my article, The Generalized Second Law implies a Quantum Singularity Theorem.
If you have any questions about the physics in the article, please feel free to leave comments on this post here. (Questions left on the Scientific American website will be answered in the comments to this post, if anywhere.)
Can you explain (for someone without a physics degree) how the speed of time causes objects to fall?
Any further reading on the subject would also be much appreciated.
Thanks for your question, Bill. I'll answer it twice, so if one explanation sounds like gibberish you can go with the other one. If both of them are incomprehesible, I'll refund the entire price you paid for them. ;-}
1. Energy is just another name for momentum in the time direction. So if there's less time near the surface of the Earth, objects also have proportionally less energy (compared to what you would expect from using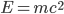
). In other words, objects at a higher altitude have a greater potential energy. But a gradient of potential energy gives a force that makes objects accelerate downwards.
2. In GR, particles move along paths described by geodesics. A geodesic is a line which is as "straight as possible" but on a curved space(time). For example, the geodesics on a sphere are great circles.
You know that in flat Euclidean space, a straight line is the shortest possible distance between two points. Similarly, in a curved space each small segment of a geodesic is the shortest distance between the two endpoints of the segment. On the other hand, on a curved spacetime, a timelike geodesic is composed of segments which are each the longest possible duration betewen the endpoints. You maximize rather than minimize the distance, because of the extra minus sign that comes into the definition of spacetime.
So if you throw a rock up into the air and it comes down again, it actually takes the path which maximizes its total time in transit between the starting and ending points (neglecting atomospheric drag). In order to experience the largest amount of time possible, the rock needs to get up away from the gravitational field of the Earth to experience less GR time dilation. But there's a limit to how high the rock can go, because the faster it goes, the more special relativity time dilation it experiences. The path it actually takes is the best compromise between these two time dilation effects. The resulting path starts by going up and then accelerates downwards. I believe that Feynman discusses this in Surely You're Joking.
Answers #1 and #2 are secretly equivalent to each other. Answer #1 uses Hamiltonian language, while answer #2 uses Lagrangian language.
Jim Hartle's Gravity textbook is pretty accessible. It's intended for undergrads, and focuses on the physically important applications of GR rather than the heavy-duty math. You might also take a look at Misner Thorne and Wheeler.
This is all very interesting material but there is one more case that I have not seen commented anywhere so here it is. In principle there would be no Grandfather paradox if we were to think about the transfer of a whole conscious entity plus a special condition of "memory erasure"! That is to say that time transfer into the past cannot be excluded at least in principle if we accompany any such construction by an additional constraint which says that any time traveller would have to suffer a serious information loss. But is that compatible with the rest of our knowledge?
Welcome, theo.
Even if your memory were erased, it would still be possible to kill your grandfather accidentally, like poor Oedipus and his dad. In fact, it might be even more likely then, since most people like their grandfathers. And even with memory erasure, your physical body would still contain physical information which could cause paradoxes.
But your statement about information loss does illustrate an important point about physics. Causality constraints (no going faster than light, no going back in time) really only apply to the transmission of information. Other types of "stuff" like e.g. electric charge don't have to obey these rules. Feynman famously championed the viewpoint where positrons are just electrons going backwards in time. And it is a measurable fact that quantum particles have a nonzero probability to go from point X to point Y faster than light. They just can't carry any information when they do. (The reason you can't use that to send a signal, is that even if there were no particle at X, you would still have a nonzero probability to measure a particle at Y due to matter-antimatter pair creation.)
Now for the questions left on the SciAm website:
jobjob writes:
Peer-reviewed, eh? Don't trust me to filter out the nonsense? You'd be surprised what can get through peer review! :-(
Anyway, you might start with "Wormholes, Time Machines, and the Weak Energy Condition", by Morris, Thorne, and Yurtsever, Phys. Rev. Lett. 61, 1446 (1988). They describe how to use time dilation effects to convert a wormhole into a time machine. Admittedly, they use Special Relativity (velocity-based) time dilation rather then General Relativity (gravitational) time dilation. But the principle is exactly the same.
That gravitational time dilation accumulates with time follows automatically from the fact that the Schwarzchild metric is unchanging with time. This is most well known in the context of the GPS system, which needs to correct for the difference in time dilation between Earth and the satellites. This is a very small effect, but as I said it accumulates with time, so it would get worse and worse if it weren't corrected for. One discussion of this is here.
ericlar asks:
We physicists tend to prove theorems in idealized situations, which may not always correspond exactly to the real world, but which we hope will nonetheless be illuminating. In the classical theorem of Hawking which I am extending, he assumes that spacetime is asymptotically flat (i.e. no Big Bang). And so do I. This is a pretty good approximation if you are just trying to create a time machine in a laboratory here in the solar system.
In the case of the real universe, what you say is quite right. The area of the past lightcone of a point today is finite (it is 0 at the present day tip, 0 at the Big Bang, and has a maximum area roughly of order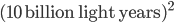
before that. (I'm just estimating by using the fact that the current age of the universe is 13.8 billion years old). Hence the difference in entropy is finite: a mere 
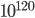or so. (I'm setting Boltzman's constant to 1, so that entropy has no units). This is much, much larger than any conceivable increase in the matter entropy inside of the lightcone (and in fact, in a homogeneous universe like ours the matter entropy would also be decreasing as the lightcone shrinks, since the entropy of the stuff inside is proportional to the volume).
Now it is true that in statistical mechanics the entropy is allowed to fluctuate downwards at times. However, a downward fluctuation of this size happens with a probability no greater than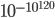
, so I wouldn't wait around for it if I were you.
Hi Aron
I enjoyed your answer much in that it also shows another point that always troubled me on how important was the historical role of probability studies for physicists to be able to invent new evasive maneuvres :). Indeed poor Oedipus, under the "hidden" guidance of the Gods perhaps, was able to perform such a feat. On the other hand, the probability of this happening again unintentionally seems overwhelmingly low given that it implicitly assumes a certain narrowing down of time and distance between the unbeknownst time traveller and his poor grandfather. In fact, the only additional axiom could perhaps just be a forbidance to travel back to a space-time volume allowing such Oedippian mishaps. Unless of course, some hidden variable theories prove correct diminishing our supposed free will in which case the accidental killing would never take place simply because of an overall "orchestration" (in which case the ancients would have had the correct idea behind the Olympians guidance, but then who knows :)
In the SA article, you mention that warp propulsion is forbidden in the same way that time travel and worm hole travel are. I believe I followed your reasoning in regard to worm holes and time travel, but I'm afraid I didn't manage to comprehend the connection in regard to warp propulsion. Could you elaborate on how the GSL prohibits a warp propulsion technology along the lines of what Alcubierre proposed? Thank you.
Welcome, William.
It's understandable that you didn't get the connection, since I didn't actually explain it. I just said you can't do it for "similar reasons". The construction in my paper is a bit more complicated than for the case of time machines or traversable wormholes, although the basic idea of applying the GSL is the same.
I define a warp drive as a region of curved spacetime where trajectories that travel through the region (from past infinity to future infinity) can get through faster than curves which don't go through that region. The Alcubierre warp drive would be an example of this.
The first step is to identify a "fastest possible" lightray L passing through the warp drive. Such a geodesic is always "achronal", meaning that no two points on it can be connected by a timelike curve. Since L is infinitely long in both directions, it defines both a "future horizon H+" (the boundary of the region which can send a signal to points on L) and a "past horizon H-" (the boundary of the region to which points on L can send a signal). In fact, L actually lies on both H+ and H- (which are therefore at least partly touching each other).
H+, because it is a future horizon, obeys the GSL, so its entropy is increasing with time. H-, because it is a past horizon, actually obeys the time reverse of the GSL, so that its entropy is decreasing with time. (That may seem totally weird, since normally the Second Law is only supposed to work in one time direction, but in the case of the GSL you can actually make sense of it going in both directions, since the GSL only applies to future horizons and its time reverse only applies to past horizons.)
But H+ and H- touch. At the place where they touch, one of them has increasing entropy and the other has decreasing entropy. From this you can get a contradiction. (Their rate of entropy increase doesn't have to agree exactly, due to the fact that H+ and H- can bend away from each other at the place where they touch, but if they do bend away from each other, this tends to make the entropy of H- increase faster than the entropy of H+, so that doesn't help.)
I think I understand. The part I was tripping up on, I think, was trying to comprehend what kind of horizon we were dealing with. For some reason, the horizon concept is easier to grasp when thinking about black holes, worm holes, and time machines. Also, it's somehow easy to forget that every event has some kind of horizon with rules that can't be violated.
Thanks so much, sir, for your quick and helpful response.
Please forgive me for asking another question, but these two just occurred to me...
If a ship with an Alcubierre drive were built and tested, what would its failure look like? Is it simply impossible to construct such a drive? Or could it be build and switched on, but it would simply fail to warp space? Or would it be like some perpetual motion machines where it can operate for a few moments because of an initial push, but very quickly it would grind to a halt?
And also, what impact has any of this (if any) upon the prospect of another staple of science fiction, anti-gravity technology?
William,
Right. In the case of a warp drive, the horizon in question would be a (perturbation to) a Rindler horizon of a lightray (or accelerating observer), which I mentioned in my paper. These exist even for flat Minkowski spacetimes.
No need to ask forgiveness; answering people's physics questions is part of why I opened up comments in the first place. If at some point I have no time to answer a legitimate question it will be my own responsibility to draw the line. It's hard to answer your question outside the context of some actual proposal for how to build a warp drive, but I'll make some general reflections.
All Alcubierre did was write down a metric which looks like a warp drive, and then calculated the needed stress-energy tensor to support that gravitational field. You can always do this using the Einstein equation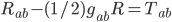
, which relates the spacetime curvature on the left-hand side to the matter stress-energy on the right-hand side. So it's hard to prove anything really interesting in GR without using an energy condition, since otherwise any metric is a legal solution.
In particular, Alcubierre found that you needed a large amount of negative energy to support the warp drive. So the moral of the story seems to be, roughly, that there simply doesn't exist any actual type of matter configuration in which there is negative energy by itself (unbalanced by positive energy of a type that would spoil the warp drive), due to the fact that QFT places constraints on the allowed relationship between the energy flux and the entropy of various regions.
Antigravity is closely connected to negative energies (which would cause repulsion). One of the other consequences of the GSL I mention in my paper is a ban on negative mass objects. But the relationship is not completely simple, since in GR tension can also cause repulsion. For example, if you have a 2-dimensional flat "domain wall" with tension in each direction equal to the energy (which can happen in certain new but reasonable laws of physics where a symmetry is broken in different ways on either side) then because there are 2 dimensions worth of tension and only one dimension worth of energy density (in GR energy density is associated with the time dimension), the antigravity effects actually win and one finds that there would be a repulsive force pushing things away from the domain wall. (This repulsive force is constant everywhere outside the wall).
[Some typos and erroneous words corrected--AW]
Got it. Thanks again!
With reference to your Scientific American article, is it correct to equate your 'horizon' ("the boundary of what can be seen by [the later end of] the CTC") with the 'past light cone' more familiar from descriptions of Special and General Relativity?
If so I'd appreciate your thoughts on why the following two past light cones might have a different impact on entropy:
a) the one related to the observer in your article leaping into the later end of the CTC (again); and
b) the one related to an observer standing up from their desk to get a cup of coffee (me, shortly - I hope).
More specifically:
I assume it's reasonable to treat the shrinkage-at-light-speed of the past light cone horizon in b) as just one of an essentially infinite number of very normal, daily life similar past light cone shrinkings. If you believe space is digital then all points in space-time form the apex of a previously-shrinking-at-light-speed past light cone (this may or may not be an infinite number) whereas if analogue space is more to your taste there exists an infinite continuum of such things (whatever that would actually mean). How does the past light cone horizon that separates the fates of the earlier and the later advertisements in your article differ from any of these with respect to entropy? It seems to me that either all possible past light cone create this infinite (or very, very large, in a 'real' universe) entropy problem or none do - including the one in your article.
What am I missing?
Welcome, Robin.
The thing you are missing is that a causal horizon is defined as the boundary of the past of a worldline which is extended infinitely far to the future. Thus, not all null surfaces are horizons---in particular, the past lightcone of a point is not a horizon, so it isn't a problem that it's area is shrinking. The GSL only says that the entropy of horizons (plus the matter outside of them) increases.
This might seem like an ad hoc stipulation, but in fact various thought experiments seem to indicate that this is the right definition of a causal horizon if you want to be able to prove the GSL. In various other specific contexts, you can show that causal horizons obey the GSL but random null surfacs don't.
In the case of the CTC, there exists a worldline which can be extended infinitely far because it cycles around the CTC over and over again. Without the CTC, that couldn't happen.
Many thanks Aron: something new to read up on and explore!