[Fixed typo in Schrodinger's equation below—AW]
Previously I talked about interference, the chief weird thing about QM that makes it different from Classical Mechanics. You have to think about complex-valued "amplitudes", from which you derive (real-valued) probabilities. From this you can also derive the notion of a Hilbert Space of states. We discussed the space of states for the polarization of a photon (a 2 state system), and how there are many different choices of "basis", representing different ways of identifying a mutually exclusive set of two possibilities.
Now let's consider a more complicated system: a single particle moving around in empty space. There are infinitely many states, because space is a continuum. Hence we need to use an infinite dimensional Hilbert space. This is harder to visualize than a two-dimensional one, but it will still be true that, in any given basis, each state can be regarded as a quantum superposition of a bunch of possibilities.
There are many possible choices of basis, but two of them are particularly nice. You can choose to either express the system as superposition of position states, or as a superposition of momentum states, but you can't specify both at the same time, because they are two different bases of the Hilbert Space! This is the origin of the Heisenberg Uncertainty Principle.
Of course, since the position and momentum are continuous variables, the probability of having any particular exact value of position or momentum is always 0. So we have to generalize the framework slightly and talk about amplitude densities. (However, there are other choices of basis where you don't have to do that).
An amplitude density is an amplitude per unit square-root-of-volume. I know these units sound a bit strange, but that way when you square it, you get a probability per unit volume, which is as things should be for purposes of doing measurements. The amplitude density is more commonly called the wavefunction of the particle. So the wavefunction can be written as a function of position: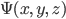 
, or as a function of momentum: 
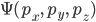, but not both at the same time. However, if you know one of them, you can calculate the other one by a Fourier transform (should you be lucky enough to know what that is).
If you have multiple particles, you shouldn't think that each particle has a separate wavefunction. Instead, you use a single wavefunction which depends on the positions (or momenta) of all of the particles. For example, if there are two different particles which we'll call #1 and #2, then you'd write:
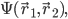
particles will live in 
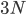-dimensions, assuming that space is 3 dimensional.)
(Given these two particles, it might be that the wavefunction factorizes, so that
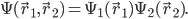
Now the two particles might be either different type, or the same type. One of the principles of particle physics is that apart from a limited number of attributes such as position/momentum, "spin", and a few other things, all particles of a given type are identical. (E.g. all electrons have identical properties, and all photons also have identical properties.)
If the two particles are identical, then it shouldn't make any difference which particle we choose to label as "1" and which we choose to label as "2". So there should be a symmetry of the wavefunction if we switch the two particles. (Remember, in QM we have interference whenever two histories end up in the same place, so to get things right we have to obsess about exactly when two situations count as exactly the same, and when they don't.) There are two different ways to implement this symmetry. The obvious thing to do is to say that:
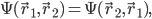
Another, more perverse way to implement the symmetry is to insert a minus sign:
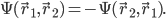
So photons are strictly identical, while electrons are almost identical, but you get a minus sign if you switch them. But remember, the overall phase of a QM system doesn't matter. So you won't actually notice anything weird if you definitely switch two fermions. The minus sign only matters in situations where they might-or-might-not have gotten switched, because then the interference between the two histories will be different.
A somewhat more straightforward implication is that no two identical fermions are ever in exactly the same position, because then the weird antisymmetry tells us that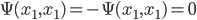 
. This is a special case of the Pauli Exclusion Principle, which is the reason for the Periodic Table. Since electrons can be either "spin up" or "spin down", you can only put 2 distinct electrons in each energy level of an atom. Then the energy levels get full, and you have to put the electrons into higher energy shells.
Bosons, on the other hand, are gregarious and love to be in the same place. Or rather, to speak less anthropomorphically, their probability to be in the same place is greater than you would expect from classical probability theory. This is what makes lasers (a bunch of photons all in the same state) practically possible.
I've mentioned "spin" several times, but I haven't actually said what it is. In QM, some particles also have an intrinsic angular momentum or polarization, which gives them a certain sort of directionality in space (even though they are point particles). Unlike a lot of the cute terms used in particle physics such as "color" or "charm", the term "spin" really does refer to actual literal angular momentum. But it works in a weird way. The angular momentum along any axis is quantized, meaning it has to be either an integer or an integer + 1/2 (times the Planck constant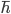 
). The maximum possible angular momentum along any axis is called the "spin" of the particle.
In Nature, there is a rule called spin-statistics which says that particles with integer spin are always bosons, and particles with half-integer spin are always fermions. (You can prove this rule mathematically in QFT, but it requires Special Relativity and some additional physical assumptions.)
Every known fundamental fermion is spin 1/2, which means that along any given axis it is either spinning clockwise (a.k.a. "up" or +1/2) or counterclockwise (a.k.a. "down" or -1/2). You only get to specify the spin along one axis, say the vertical one. This is not to say that an electron can't spin "left", "right", "in", or "out", but these states are quantum superpositions of the "up" and "down" states. By rotational symmetry, we could pick a different basis (e.g. right / left) and instead think of up and down as superpositions of right and left. The (2 complex dimensions = 4 real dimensions) space of possible electron spins is called a spinor.
A spinor needs to be rotated by 720º (2 full circles) to get back to its original state. Yes, you read that right. If you only rotate it by 360º (1 full circle) then it comes back to itself with an extra minus sign in the amplitude. Just like when you switch two electrons. They're just perverse that way.
Most of the fundamental bosons are spin 1, so their polarization is given by a vector, as in the case of the photon which we discussed last time. Vectors get a minus sign when you rotate them by 180º, and return back to the way they were after 360º, just like you were taught in school.
However, the Higgs boson (which gives mass to most of the other fundamental particles) is a spin-0 or scalar field. That means it doesn't change at all when you rotate it. On the other hand, the graviton is a spin-2 particle, which means it gets a minus sign when you rotate it 90º, and goes to itself under 180º. Its polarization is described by a matrix, but let's not get into that here.
The bottom line is that for anything more complicated than a scalar field, in addition to the position or momentum variables you also need to include the spin degrees of freedom. So if we have one electron and one photon, the wavefunction will look like e.g.
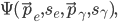
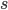represents the spin of the electron or photon along e.g. the z-axis. This is still a 6 dimensional space since 
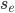can only take the values 
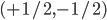, and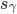 
can only take the values 
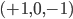. (Incidentally, since the photon is massless, its spin is always required to be perpendicular to its momentum, so there are really only 2 polarization states, not 3. But the explanation of this involves relativity and gauge symmetry and a bunch of other things from QFT...)
There is also a third kind of basis, distinct in general from both the position and the momentum basis, in which time evolution is particularly simple. This is the basis where the energy of the system takes on a definite value. In this basis, the only thing that changes is the phase of each energy state. The phase changes with time at a speed proportional to the energy.
So one way to specify the dynamics of a QM system is simply to say what the formula for the energy 
is, as a function of all the positions and momenta of all the particles in the problem. (You think of this an operator, a gadget which acts on the wavefunction to get another wavefunction. So if you are in the position basis, the "momentum operator" is given by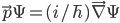 
, which is equivalent to switching from the position to the momentum basis, multiplying by p, and then switching back.) Then you can figure out how the wavefunction changes with time by using the Schrodinger equation:
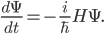
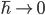limit, you recover classical mechanics.
There is also a "path integral" picture due to Feynman, related to the Lagrangian or "Least Action" approach to physics mentioned at the same link, where you assign to each history an amplitude proportional to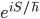 
, where 
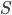is the action. This approach is actually more closely related to the picture I started with in part I!
In this sense, Quantum Mechanics is a fulfillment of Classical Mechanics, just as (in Christian doctrine) the New Covenant fulfills the Old Covenant. That is, the new model justifies the quirky, previously-inexplicable features of the old model, in terms of a more basic (yet also more mysterious) set of ideas. Concepts such as action, energy, momentum, the associated conservation laws, and so on, all follow naturally from the interference of wavefunctions over space and time.
Incidentally, there's a very important flaw in what I've told you so far. Generally speaking, in modern physics it's better to think of the universe as being made of fields, not particles! This is the subject of Quantum Field Theory. The idea is that we should really think of the universe as being made of some finite number of types of fields (e.g. the electron field, the photon/EM field, the quark field, etc.). Consider a scalar field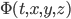 
, which is basically a function of the spacetime points. If we want to keep track of the amplitude for any possible configuration of the field, then we really need our wavefunction to be a function of all possible configurations of 
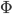at one moment of time. Morally speaking (i.e. I am about to make certain dreadful oversimplifications) this means that the state of the universe at one time is something more like:
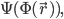
QFT gets kind of complicated, but the advantages are that 1) it is easier to make it compatible with Special Relativity, and 2) it allows one to consider situations where particles are created and destroyed, e.g. an electron can emit or absorb a photon. Since this happens all the time in the real world, that's kind of important!
But as long as you're dealing with situations where the particles are all going much slower than the speed of light, and none of them decay into other particles, you can use QM as described above. (Perhaps I shouldn't have given the photon as an example, because it always travels at the speed of light and is never nonrelativistic.)
Aron:
When you say: "The idea is that we should really think of the universe as being a finite collection of fields." does that translate into the statement: the observable universe that is within 13.80 billion light years of us, + or - o.o4 bn years is finite? Does the "finiteness" apply to any universe outside the observable range.
To non-physicists like me, always fascinating, this subject.
Thanks
TY,
I meant there are (as far as we know) only a finite number of kinds of fields: one field for each kind of "fundamental particle" in Nature, e.g. electrons, quarks etc. Nothing about whether the universe is finite or infinite in spatial size! I've edited the post to make that clearer.
Aron in this discussion are you going to discuss the "Everett Many World Views"? If yes, then I would appreciate you addressing what appears to me a major problem with it. The problem I perceive with all the many different branches being realized or coming into existence, is that it appears that conservation of energy is violated. The new branches are points at which new universes come into existence. Doesn’t this violate conservation of energy? If you answer is energy is conserved in each new universe, then what about the total energy?
Steve,
Actually, conservation of mass-energy won't work as a criticism of MWI, and for a rather surprising reason... because for the universe as a whole mass-energy isn't conserved or even well-defined (at least, not in general). Formally, this can be shown from continuity equations which can be expressed in two forms; 1) As differential equations at any given space-time event, or; 2) As "flux integral" equations defined over the surface of a space-time volume. Using the former approach in the usual manner gives,
Where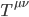
is the stress-energy-momentum tensor. For low velocities this gives the usual conservation of mass and/or energy laws one is taught in freshman physics. More generally it leads to conservation of 4-momentum, which blurs the distinction between mass, energy, and momentum somewhat. The interesting thing is that although 
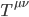is a tensor, the divergence on the left is not... it's something physicists refer to as a pseudotensor and it only vanishes in flat space-times. A continuity equation for mass-energy in curved space-time as well must take the curvature into account, and to do that we must express it as a covariant divergence,
This equation yields a tensor divergence that's valid for all space-time. But in this equation neither mass, energy, more momentum densities, or their corresponding fluxes are well-defined. They can be zero, infinite, or anything in-between depending on one's choice of reference frame. And if we apply Noether's theorem to this situation we find that the associated conserved quantities (the Noether currents) aren't well-defined in any of these quantities either. Ergo, energy is conserved here and now, and there and then... but for the universe as a whole it's neither well-defined, nor conserved, so there's no reason to expect MWI to conserve it either. The one exception to this would be if the universe is closed, in which case it doesn't meaningfully have a boundary on which flux integrals can be defined, so its energy is de-facto zero. Aron has written about this here.
So... this argument doesn't work. But IMHO, MWI is still bat-s*** crazy, and we don't need conservation of energy to show that. :-) Best.
Steve,
I am indeed heading towards a discussion (and critique) of the MWI. However, I don't think conservation of energy is a good objection to make against MWI.
First of all, the real claim of MWI is that you just evolve the wavefunction by the Schrodinger equation, without ever "collapsing" it when there's a measurement. The whole "branching worlds" thing is just an intuitive picture for describing the wavefunction, which isn't completely precise. (Indeed, Everett never used the phrase "many worlds"; that phrase was coined by Bryce de Witt.)
Secondly, note that Energy Conservation isn't some sort of metaphysical principle deduced abstractly. It's (1) an experimentally measured fact, which is also (2) a mathematical property of certain kinds of physics equations. So as long as a theory agrees with experiment, it can (and should) intepret "conservation of energy" in whatever way makes the most sense given its conceptual framework. So if it turns out that energy is conserved in "each world" and you shouldn't add up to get the total energy, then that would just be how it is.
However, by the Time-Energy uncertainty relation, it doesn't really make sense to assign a precise energy to a system which is changing with time. Instead, such a system should be thought of as a quantum superposition of a bunch of states with definite energy.
So consider the wavefunction, evolving by Schrodinger's equation. It has the property that if you calculate the probability density associated with any particular energy, it remains the same for all time. This is one way to state the conservation of energy in QM.
On the other hand, theories of "objective collapse" (in which the wavefunction gets reduced at specific times when some triggering event happens) probably would violate conservation of energy (in the sense defined above). So if anything, that argument points in the other direction.
Scott,
, as I mentioned in the post above.
While your answer is technically correct, it seems confusing to bring in General Relativity and Cosmology, when the question had to do specifically with Quantum Mechanics only. In QM, there is normally a well-defined energy operator
"Energy Conservation isn't some sort of metaphysical principle deduced abstractly. It's (1) an experimentally measured fact, which is also (2) a mathematical property of certain kinds of physics equation"
Isn't this contradicted by the actual practice in physics? One assumes energy conservation to hold true and and to make it hold, the physicists even postulate new particles, e.g. neutrino and dark matter/dark energy.
Aron, I agree... my approach was unusual, and in another context would be quite confusing. I took it here because if I understood him correctly, Steven's question wasn't just about energy conservation in QM per se, but specifically in regard to branching universes. If we measure some observable for which there are, say, 10 eigenstates, MWI says that in making that observation we go from this universe to 10 separate parallel universes, all identical up to the associated eigenstates. What I believe he was asking was, how do we go from one universe to 10 nearly identical universes without violating energy conservation? Viewed from that perspective, the fact that for the universe as a whole, energy is neither well-defined nor conserved, and thus needn't be conserved in any branching, seemed apropos. But yes, apart from this context, bringing GR into a discussion of QM measurement would be rather odd.
Great post BTW! :-)
Scott Church,
It seems that measurement remains an undefined singularity even in MVI--only instead of wavefunction collapse, one gets branching of entire universes.
This would seem to negate the unique selling point of MVI. What am I missing?
Mactoul,
The principle of energy conservation is very venerable, and preserving it has (as you say) often been a guide to new physics. Nevertheless, in principle it is possible (even if unlikely) that some future new theory of physics would require us to give it up. Ultimately, experiment rules in science.
(But only ultimately. In the short run, it's a lot more likely you just didn't do the experiment right, or there's some other kind of energy you haven't accounted for.)
There are mathematical derivations of energy conservation from certain sets of assumptions. But those assumptions might themselves turn out to be experimentally wrong! So it's a posteriori.
With regard to your other question, what you're missing is that "Many Worlds" is just a misnomer for the following view:
1. The wavefunction never collapses,
2. All components of the wavefunction are equally physically real,
3. Nevertheless we should use the Born rule to determine our odds of experiencing any particular measurement outcome.
There are no "branching worlds" anywhere, except to the extent implied by belief #2.
Aron, from the standpoint of the wave function of the universe (including us) and counterfactual definiteness, my understanding of MWI was that belief #2 does imply branching worlds... as in, there's a universe (or if you rather, an equally real parallel branch of this one) where I didn't just take a drink of water, another where I'm an atheist circus clown, etc. etc. If that's not the case, then what is the correct understanding of #1 and #2 as they relate to our experience?
[Geez... I hope I haven't been fundamentally misunderstanding this for years! :O ]
Scott,
No, I'm not saying you've been wrong all these years. There is indeed a sense in which belief #2 does imply branching worlds. For example, if we start with the state of the universe prior to the 2000 election, and run it forwards using Schrodinger's equation, it would turn into a quantum superpositions of situations in which e.g. Bush won in 2000 and in which Gore won in 2000, and then there would be another piece of the wavefunction with much smaller amplitude in which Nader wins.
The thing I'm trying to guard against is the idea that MWI involves some sort of "branching process" which is DISTINCT from Schrodinger evolution of the wavefunction. Instead, it's simply a description of what Schrodinger evolution does.
The picture in which there is branching into a set of different worlds is a somewhat loose description, among other things because it requires a particular choice of basis. Now, the phenomenon of decoherence means that for purposes of macroscopic events, in practice there is no interference between branches of the wavefunction which differ by a large number of particles. But in principle there would always be a tiny amount of interference.
Thanks Aron! I do understand the Schrodinger equation in that sense as well. I just wanted to make sure I wasn't fundamentally misunderstanding the "branching into different worlds" part and its implications, even if that's not the best description of it. So... it really is as bat-s*** crazy as I've always imagined... I don't much relish the idea of being an atheist circus clown somewhere. :-)
"there's some other kind of energy you haven't accounted for."
Or the physicists are free to postulate entirely new energies so as to keep the law of energy conservation. Eg the case of dark energy.
This procedure vitiates against the idea that energy conservation is experimentally falsifiable.
MVI operates with the wavefunction of the world (WoW).
Is WoW a meaningful thing?
A wavefunction encapsulates the knowledge that an observer has regarding a physical system. If so, how could the entire universe be describable with a wavefunction? The observer needs to stand outside the universe if WoW is to be defined but the very notion of "standing outside the universe" is absurd.
Mactoul,
First of all, what does "MVI" stand for? Is it the "Many Vorlds Interpretation"? ;-)
This is a substantive claim about interpretation of QM which must be justified, not dogmatically assumed.
Also, do electrons cease to have a wavefunction when no observer is thinking about them???
Just because we can't do it, doesn't mean we couldn't imagine what it would be like if we did do it. How are you justified in using the word "universe", if you cannot make the mental motion of imagining everything that exists taken as a whole?
Also, isn't God outside the universe, in a sense?
This is a reasonable thing to do precisely because dark energy is postulated to obey some specific, simple law of motion. (The simplest hypothesis is that it is simply a constant energy density of empty space.)
If the laws of physics were simpler in a form which gives up energy conservation, we would give it up.
Just because we are resistant to giving up foundational principles for light reasons, doesn't mean we wouldn't do it if there was sufficient motivation to do so. We gave up several foundational principles of Classical Mechanics when we switched to QM, because the evidence for doing so was compelling.
"do electrons cease to have a wavefunction when no observer is thinking about them?"
To my understanding, wave functions are mathematical objects and not physical objects like electrons. It is like asking whether the number system ceases to exist if nobody is thinking about it.
"How are you justified in using the word "universe","
Metaphysically, we can define "universe" as the totality of consistently interacting things but empirically it is hard to get a handle on the "universe" for obvious reasons. Each use of "universe" needs to be justified in physics. It is especially problematic in QM as QM places special significance to "observers".
And if you claim that decoherence gets rid of this observer-dependence, it is my understanding that for a wavefunction to undergo decoherence, it requires an environment. If so, how could the WoW ever decohere?
"Also, isn't God outside the universe, in a sense?"
God isn't mentioned in the QM textbooks, at least should not be. QM should be able to stand on its own, like any other honest science.
Aron,
Have you seen the following paper by Susskind which was discussed on a physics blog I visit. I would be interested in your reaction to it, particularly to the last line, when you have had time to read it. Thanks.
arXiv:1604.02589v1 [hep-th] 9 Apr 2016
Susskind:
“It is obvious that the Copenhagen Interpretation cannot be the last word. The universe is filled with subsystems, any one of which can play the role of observer. There is no place in the laws of quantum mechanics for wave function collapse; the only thing that happens is that the overall wave function evolves unitarily and becomes more and more entangled. The universe is an immensely complicated network of entangled subsystems, and only in some approximation can we single out a particular subsystem as THE OBSERVER”
Mactoul,
A system does not require an external enviorment to decohere. If it is sufficiently complicated, it can decohere itself. An environment is just one example of a complicated system.
I agree that God need not be mentioned in QM textbooks. (And I agree that invoking him to explain collapse is silly.) But you do believe in God, yes? If so, surely you must also accept the statement: "QM is true because it is God's will to create a quantum mechanical universe". That would be a theological explanation of a physical theory. Maybe it's not a very helpful or useful explanation, since it isn't particularly obvious why God should have made this decision (other then, perhaps, it being necessary for life). But I don't see how a Theist who believes that God is the Creator could deny that this explanation is true as far as it goes.
kashyap,
I have seen it. The particular point that we need a way of understanding the QM of the whole universe was made by many people before Susskind. (For example, de Witt.) The more interesting part of the paper is its attempt to relate entanglement to geometrical structures such as wormholes, continuing the hypothesis of Mark Van Raamsdonk. (For a pop article explaining his idea, see here.)
This idea is definitely interesting, but I don't think it's possible to get wormholes from nothing but entanglement without additional inputs. Not without giving up linearity of QM, which I am reluctant to do. I've set out my point of view in a paper with Don Maorlf.
Aron,
"If it is sufficiently complicated, it can decohere itself. "
Is it something that has been demonstrated or is it a supposition stemming from the fact that complicated systems are generally classical?
I wonder how would you interpret Schroedinger's Cat paradox. The crux lies in a coherent yet complex system. Would you say that the paradox is mistaken?
Aron,
"QM is true because it is God's will to create a quantum mechanical universe". That would be a theological explanation of a physical theory.
Perhaps, But I am unclear as to why theology keeps intruding in a purely physical discussion of wave function collapse.
Aron,
Perhaps you will discuss wave function collapse in greater detail soon. To my mind, there is an unsurmountable gulf between a double-silt experiment and statements of the type--"in one branch of the universal wave function, Gore won in 2000 and in another branch Bush won."
I am skeptical of the very loose usage of the term "observer" as exemplified in the Suskind quote above
"The universe is filled with subsystems, any one of which can play the role of observer."
" the phenomenon of decoherence means that for purposes of macroscopic events, in practice there is no interference between branches of the wavefunction which differ by a large number of particles. But in principle there would always be a tiny amount of interference."
" if we start with the state of the universe prior to the 2000 election, and run it forwards using Schrodinger's equation, it would turn into a quantum superpositions of situations in which e.g. Bush won in 2000 and in which Gore won in 2000, and then there would be another piece of the wavefunction with much smaller amplitude in which Nader wins."
BUT in 2000, it was Bush than won. Not Gore, not Nader. The wave function did collapse.
Is it really meaningful to INSIST that somewhere, in some parallel universe or "branch", it was Gore that won?
Is physics now in the business of asserting imaginary events?
Mactoul,
I think you've misunderstood me. I don't believe that there is another universe out there where Gore won the presidential election. Like you, I think that is crazy. But that is what advocates of Many Worlds believe.
And the reason they believe it---and this is a fact which is acknowledged by all sides---is that if you allow the wavefunction to evolve via Schrodinger's equation alone, it splits into multiple branches corresponding to different outcomes. As I said, nobody denies this fact!
To deny Many Worlds coherently, I think you have to either (a) assert that in some way the wavefunction "collapses" down to one of the branches via some physical process, or (b) deny that the wavefunction gives a complete objective description of reality (as in Bohmian or quantum Bayesian intepretations.) There are reasonable philosophers of physics who adopt these points of view.
Decoherence is just the fact that these branches don't exhibit much interference when they differ from each other in sufficiently complex ways. This has been shown mathematically from analysis of Schrodinger's equation in particular examples, and also matches to experiment to the extent that it can be tested. QM is very well established by experiment in microscopic systems, including its predictions (in that context) about decoherence.
Decoherence is not the same as the statement that the wavefunction collapses (nor is it the same as the statement that it does not collapse). But it does have the unfortunate implication that if the wavefunction does collapse in sufficiently complex systems, it would be practically impossible to experimentally measure that fact. This is one reason why the diffent interpretations of QM can't be resolved by experiment!
PS I would slightly prefer if you try to write one long response instead of many short ones so it doesn't clog the "new comments" feature in the side bar.
Aron,
Clearly this business with collapse, decoherence and branches confuses me to no end. Some remarks:
1) Splitting branches in MWI-- why the splitting and what determines when the branches should split?
As I understand, Schroedinger is a linear equation so why it should have splitting branches at all? Why just not a continued superposition?
1A) Do the branches split because they mutually decohere?
2) You say to deny MWI coherently one needs to
"(a) assert that in some way the wavefunction "collapses" down to one of the branches via some physical process,"
You don't think the Copenhagen type collapse is a coherent alternative? You rule out Observers of the Heisenberg-Bohr type absolutely?
And the reason being that Copenhagen and its observers do not allow you to posit Wavefunction of the
World (WoW)?
3) Take decoherence in an isolated system i.e. not WoW. Now, as you say, decoherence is not the wavefunction collapse (esp of Copenhagen type). Then what is the wavefunction post-decoherence?
Eg in Schrodinger Cat, the wave function is superposition of alive and dead cat. The post-collapse situation is cat either alive or dead (as per Copenhagen)
But what is the decoherent solution?
Mactoul,
1.
That is exactly the point! The equation is linear, and therefore there is a continued superposition between different possibilities (even if the possibilities evolve to dramatically different physical configurations as in the case of Shrodinger's cat).
This fact (that there is a continued linear superposition) and nothing other than this fact, is what MWI people mean by talking about branches of the wavefunction! This, and nothing other than this.
Now what about splitting? Accoriding to MWI, this is an imprecise, colloquial term to refer to one of the following sets of events (or both together):
A) Now, when you evolve a wavefunction by the linear Shrodinger's equation, it often happens that a state which takes on a definite value (in one particular basis) evolves to a superposition of different states (in that same basis) at a later time. (Similarly there can be situations where a superposition of two states merges into one state.)
B) Decoherence is just the statement that when two terms in the superposition evolve to become sufficiently physically distinct (e.g. many distinct particles are in a different location in the two situations, in a way that is unlikely to be reversible by any reasonable process) then the amount of interference between the two terms drops to (nearly) zero.
Therefore (say MWI people) the different branches cease to interact at this point, and therefore for practical purposes you can ignore all of the other branches except for the one which you are living on.
What you have to realize is that the term "branching" is not really an official part of the MWI philosophy. It's just a term used in popular descriptions of MWI to describe the process which begins with (A) and ends with (B). Everyone agrees on the math of how Shrodinger's equation works, but not everyone agrees on how it should be interpreted (or whether there are some additional physical properties).
2.
No, I regard it as an example of a theory of type in which collapse occurs as an objective physical process.
3. The wavefunction becomes decoherent when---after evolving via Shrodinger's equation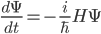
, it reaches a configuration consisting of the superposition of two or more terms which no longer significantly interfere with each other. Nevertheless, post-decoherence it continues to be a superposition of these different terms. (Contrast to an objective collapse hypothesis, where all but one of the superposed terms goes away, at some point).
"post-decoherence it continues to be a superposition of these different terms."
Can it be that I am saved in one branch and not saved in another branch?
That Jesus was crucified in one branch and not crucified in another branch?
Your insistence that the reality is really a wave function or fields-which are all mathematical objects, I still find it problematic.
It is a species of Platonist idealism--that the ultimate reality is numbers and not things.
In my view, one will always have to face unresolvable paradoxes and unpalatable choices, when one sticks with any species of idealism.
Macotul,
There seems to be a communication gap between us, because I never insisted that "reality is really a wavefunction" nor do I subscribe to the Many Worlds Interpretation of QM. I have simply been describing the uncontroversial facts about what you get mathematically if you evolve the wavefunction by Schrodinger's equation, without making any claim about interpretation or what really happens. Many Worlds people claim that the "branching" of the wavefunction implies that every possible historical event really happens, but to repeat myself again, I do not believe in the Many Worlds Interpretation!
I am agnostic about whether the wavefunction collapses in some objective sense or whether we need to simply shift our intepretation of the wavefunction away from being a complete description of the universe (it seems you are sympathetic to the latter). So I don't think we disagree as much as you think we do.
As for your questions, they are properly directed to a person who believes in both MWI and Christianity. The only person I know of in the intersection of these categories is St. Don Page. So you should really be asking him these questions, not me!
PS I am also not an idealist in the sense you mention, but in my experience sticking with any viewpoint in philosophy leads to "unresolvable paradoxes and unpalatable choices". That doesn't mean we shouldn't try to select the viewpoint which makes the most sense, but it does that the universe is hard to understand and in some ways very foreign to our common sense intuitions.
Aron alerted me to your comment, Mactoul. As is also William Wootters, who co-discovered the no-cloning theorem, I am indeed a Christian who believes in the MWI (at least to the extent that there is no collapse of the wavefunction, which evolves unitarily, as Aron described it; some adherents of the MWI propose that there is a preferred basis that gives objective splitting, but I don't). I do bite the bullet and believe that there are Don Page experiences of being saved (one I have in my memory of my initial decision to follow Christ and one in my present experience of being in Christ), but that the uncollapsed wavefunction does have other experiences in which Don Page is not saved. (However, I have personally become sceptical of the tradition that interprets the Bible to imply that those who are lost spend an everlasting conscious existence in Hell, since I believe many Biblical verses can naturally be taken to mean that eventually "every knee should bow, in heaven and on earth and under the earth, and every tongue acknowledge that Jesus Christ is Lord, to the glory of God the Father" [the Apostle Paul's Letter to the Philippians, chapter 2, verses 10-11], after perhaps needing time in Hell for the repentance and cleansing of sins not repented and cleansed in this life, so that everyone will eventually acknowledge Christ and willingly receive the salvation He generously offers and paid for on the Cross, though it would be much less painful to receive this earlier than later.)
On the other hand, my tentative view is that God arranged the quantum state of the universe so that Jesus Christ did suffer and die for our sins in all components of the quantum state. (It also seems likely to me that the Crucifixion, and especially the Resurrection, was a sufficiently important occasion for God to alter the normal way He evolves the wavefunction, so that this was a miracle not only in being a marvelous action by God, like the birth of any child, but also in being a change in the usual ways in which God acts in orderly ways that we now might call the laws of physics.)
My own interpretation of the MWI is given in Mindless Sensationalism: A Quantum Framework for Consciousness. I have also written A Theological Argument for an Everett Multiverse that you might find interesting. I have presented talks on this subject at Ryerson University and the 2014 annual ASA/CSCA/CiS meeting.
Aron,
I do understand that you do not advocate MWI but you seem to grant MWI a worthiness that you do not grant to the Copenhagen. I am puzzled why. Whatever the drawbacks of Copenhagen, they pale before the extraordinary demands MWI makes on us, if we regard a measure of physical reality to what the interpretations posit, and not merely as mathematical tool.
My question is whether this disregard of Copenhagen is due to the fact that Copenhagen does not lend itself to cosmological investigations i.e. the wavefunction of the universe.
Don N Page,
You have interesting views. In particular,
"God arranged the quantum state of the universe "
As I see it, this is viewing God in an excessively anthropomorphic terms, almost as conceiving of God as a demiurge who uses the existing laws and matter to fashion things. Also, it does not gel with the idea that the Resurrection was a miracle. For miracles are inexplicable events. To explain a miracle in terms of, say a quantum state, however singular and pre-arranged, is to explain away the miracle. It is no longer a miracle but an unusual event which is however fully describable by physics.
Don N Page,
I am reading your very interesting paper and I have plenty of questions. Perhaps we can impose upon Aron.
You write
"I shall assume that an external world exists in some sense and is helpful in explaining our conscious experiences"
I should have thought that the mere matter of writing a paper on a computer itself presupposes and affirms the existence of the external world and other minds.
After all, you choose to write a paper for other minds to read. That choice affirms the external world. One could not act if there were no external world.
Aron,
"we should really think of the universe as being made of some finite number of types of fields"
A field is just a pattern of numbers. So your claim is that universe is made up of patterns of numbers.
But how could numbers, which are ideas or concepts, make up concrete things?
This idea, being metaphysical, can not be physics, strictly speaking. That is, physics could just say that the quantitative aspects of relations between two things could be represented by fields. But physics could never say that the things themselves are fields.
Mactoul,
I agree that there is a very important philosophical distinction between the mathematical description of concepts in physics, and the physical entities which they are supposed to describe.
However, in everyday life it is not always important to distinguish these things, so the same word may be used in both contexts. Thus, the word "field" may refer either to the pattern of numbers, or by metonymy to the actual physical entity, whatever it is, which that pattern of numbers is supposed to describe. More often it refers to the latter, the actual physical entity!
Hi Aron,
Probable typo: you mention He-4 nuclei as both bosons and fermions.
Cheers, Leon
Leon,
Yikes! I meant to say He-3 for the fermion. I've fixed it now, thanks for the catch!
Hi Aron,
When can we expect the critique of Many Worlds Interpretation? This sounds like a really interesting topic.
Hi, Aron!
How do we reformulate the wavefunction and the measurement problem in terms of QFT? Does Copenhagen interpretation and indeterminism associated with the collapse still holds in QFT?