What is the world made out of? In the most usual formulations of our current best theories of physics, the answer is fields. What are those?
Well, if you know what a function is, you're already most of the way there. A function, you will recall, is a gadget where, for any number you input, you can get a number out as an output. We can write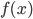 
where 
is the number you input, and 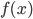is the number you output. The function 
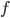itself is the rule for going from one to the other, e.g. For example 
.
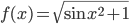Now, nothing stops you from having a function that depends on multiple numbers as input; for example the function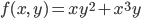 
depends on two input variables, , and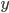 
. If there are 
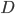input numbers, then the 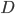-dimensional space of possible combinations of input numbers is called the domain of the function.
Also nothing stops you from having the output be a set of several numbers. In this case we would need some sort of subscript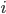 
to refer to the different possible output numbers. For example, if we had a function with one input number and three output numbers 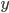, then we could write 
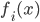, where 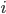takes the values 1, 2, or 3. Then 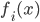would really be just a package of three different functions: 
, 
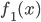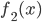, and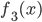 
. So if you specify the input , you get three output numbers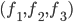 
. If there are 
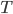different output numbers, the 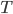dimensional space of possible outputs is called the target space.
Now a field is just a function whose domain is the points of spacetime. For example, the air temperature in a room may vary from place to place, and it may also change with time. So if you imagine checking all possible points of space in the room at all possible times, you could describe this with a temperature field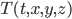 
. However, the temperature field isn't a fundamental entity that exists on its own. It subsists in a medium (air) and describes its motion. When the air molecules are moving around quickly in a random way, we say it's hot, and when they start to move around slower, we say it's getting chilly. An example of a field which actually is fundamental (as far as we know) would be the electromagnetic field. This has 6 output numbers, since the electric field can point in any of the 3 spatial directions, and the magnetic field also has 3 numbers.
For a while in the 19th century, scientists were confused about this. They thought that electromagnetic waves had to be some sort of excitation of some sort of stuff, which they called the aether. That's because they were assuming (based on physical intuitions filtered through Newtonian mechanics) that matter is something solid and massy, which interacts by striking or making contact with other things. The 20th century scientific advances partly came from realizing that its okay to describe things with abstract math. Any kind of mathematical object you write down satisfying logically consistent equations is OK, as long as it matches experiment. So electromagnetic waves don't have to be made out of anything. They just are, and other things are (partly) made out of them.
In our current best theory of particle physics, the Standard Model, there are a few dozen different kinds of fields, and all matter is explained as configurations of these fields. I can't tell you exactly how many fields there are, because it depends on how you count them. Not counting the gravitational field, there are 52 different output numbers corresponding to bosons, and 192 different output numbers corresponding to fermions (Don't worry about what these terms mean yet). So you could say that there are 244 different fields in Nature, each with one output number.
That sounds awfully complicated. But there's also a lot of symmetries in the Standard Model which relate these output numbers to each other. This includes not only the Poincaré group of spacetime symmetries, but also various internal symmetries related to the dynamics of the strong, weak, and electromagnetic forces. They are called internal because they don't move the points of spacetime around. Instead they just mutate the different kinds of output numbers into each other.
So normally, particle physicists just package the output numbers into sets, such that the numbers in each set are related by the various kinds of symmetry. (For example, the 6 different numbers of the electromagnetic field are related by rotations and Lorentz boosts.) Each of these sets is called a field. In future posts I'll give more details about the different kinds of fields. As always, questions are welcome.
UPDATE: I forgot to include the 4 vector components of the spin-1 gauge bosons, so the numbers of degrees of freedom of the bosons were wrong before. Note to Experts: These are the "off-shell" degrees of freedom before taking into consideration constraints or gauge symmetry. Note to Non-Experts: the numbers in this post are just for flavor, in order to give you the sense that there are a LOT of different fields in Nature. You won't need to understand how I got these numbers in order to enjoy future posts!
Functions are described relationship? So "fields" are not "things" but the relationships that exist in the universe? that co-exist with things?
Also, can you give me two books, sources, that you have found most helpful in your understanding of the Resurrection as history?
Thank you for your very valuable time (Blogging is a patient form of giving/sharing).
I am very grateful,
Daniel
Daniel,
I'm not sure I'd say that a function is a "relationship". I also don't know what you mean by it being "not a thing"; it seems to me that "thing" is a flexible enough word that it can be used to mean pretty much anything.
No, I meant the sort of function that comes up in math classes; the kind that you can plot on a graph. Or at least, that you could graph, if your graph paper had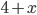
dimensions, where 4 is the number of spacetime dimensions and 
is however many output numbers there are in your function. For example, in the case of a single scalar field,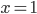 
. A scalar field is just a real number defined at each point in space and time. I guess you could say that this defines a relationship between that point of spacetime and that number, but it is the value of the field at each point which corresponds to the physically real "state" of the field. The "real number line" is not a physical thing, just a mathematical structure helpful for describing physical things.
Regarding book recommendations on the Resurrection, didn't I already answer this question in the comments to the subscribe page? (I'm not sure why you picked that place to leave your comment, but I replied in the same place).
I'm glad you appreciate my efforts.
How many numbers are associated with each kind of particle? How many are associated with the photon/electromagnetism, with the W, Z+, and Z- bosons/the weak force, with the gluons (in weird super positions with themselves? I've never really understood that...)/the strong force, and with all the different quarks and leptons and their antiparticles?
David,
Electrons and the other kinds of fermions in the Standard Model are "spinor fields" (i.e. spin 1/2), which is one possible (simple but peculiar) way in which a set of numbers can transform under rotations and Lorentz boosts.
Most fermions in the Standard Model are Dirac fermions. A "Dirac" (or 4-component) spinor field is composed of a set of 4 complex numbers (= 8 real parameters) which transform in a particularly nice way. For example, an electron is a Dirac spinor. The Dirac spinor includes the information about both electrons and positrons; complex conjugation (switching i and -i in each complex number) corresponds to switching particles and antiparticles.
(Sometimes in special cases it is possible to have a fermion field which has fewer componets. For example if you have a massless fermion (travelling at the speed of light) it is consistent to say that it always rotates clockwise (or counterclockwise) relative to its direction of motion. This is called a Weyl fermion (or 2-component spinor) and it has only 2 complex numbers. Another special case is a massive spinor which is its own antiparticle, which can be described by a Majorana spinor which has 4 real components, the same # as the Weyl spinor. People used to think the neutrinos were Weyl fermions, now it seems quite plausible they are Majorana spinors.)
It's also possible for fermions to come in multiples as a result of being charged under a nonabelian symmetry group, such as the strong force SU(3). In particular, a given flavor of quark (e.g. "up") can be either "red", "green", or "blue" under the strong force, so each quark field is actually 3 sets of Dirac fermions.
The force fields are spin-1 particles, which means that their field is a vector which can point in any of the 4 spacetime directions. So the photon field involves a set of 4 real numbers. (Real, because the photon is it's own antiparticle.) Similarly, the Z^0 particle has 4 real numbers. The W+ is the antiparticle of the W-, so together they involve a vector of 4 complex numbers. (Note, you got the W and Z mixed up in your comment; the Z is the neutral one and the W is the charged one.)
The gluons each carry one color and one anti-color. (For example, if a red-antigreen gluon were absorbed by a green quark, it would become a red quark.)
You might think that there would be 3x3 = 9 total color combinations (plus all the resulting linear combinations, which correspond to quantum superpositions of gluons). But in fact one superposition of gluons, namely:
red-antired + green-antigreen + blue antiblue
doesn't actually exist. Thus there are only 8 kinds of gluons in total, which is related to the fact that the Lie group SU(3) is 8-dimensional. The gluons also have vector polarization (just like the photon) so that is 8 x 4 = 32 real numbers.
(However, one additional subtlety arises for massless gauge fields, and that is gauge symmetry. For example in the case of a photon, any vector field which is the gradient of a scalar field is actually unphysical and can be ignored. Only the line integral of the vector field going around a loop is physical.
The effect of this is in essence to decrease the number of physical components of the vector per point of spacetime from 4 to 3. This doesn't affect the W/Z bosons since they are massive; their gauge symmetry is spontaneously broken by their interaction with the Higgs field.)
Finally the Higgs field is a scalar. Since it is charged under SU(2), it has 2 complex numbers (= 4 real numbers) prior to spontaneous symmetry breaking of the weak force, but after spontaneous symmetry breaking 3 of those numbers become the extra states of the W and Z bosons, leaving just 1 real number remaining to be the Higgs boson observed in particle accelerators.
Now you can check to see if I added up the numbers right! If anything was unclear, feel free to ask for clarification.
Can we "quantize" the temperature field, the same way that we do with the EM field? I mean, is there a quantum version of T(t,x,y,z)?
Sorry about the so many comments at the same time. It is probably inconvenient for you guys, scott and aron. But i promise the next time it will not happen.