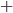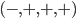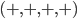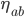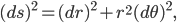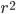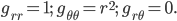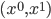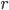Bayes' Theorem

by Aron Wall Posted on December 23, 2012

Today I'd like to talk about Bayes' Theorem, especially since it's come up in the comments section several times.  It's named after St. Thomas Bayes (rhymes with "phase").  It can be used as a general framework for evaluating the probability of some hypothesis about the world, given some evidence, and your background assumptions about the world.

Let me illustrate it with a specific and very non-original example.  The police find the body of someone who was murdered!  They find DNA evidence on the murder weapon.  So they analyze the DNA and compare it to their list of suspects.  They have a huge computer database containing 100,000 people who have previously had run-ins with the law.  They find a match!  Let's say that the DNA test only gives a false positive one out of every million (1,000,000) times.

So the prosecutor hauls the suspect into court.  He stands up in front of the jury.  "There's only a one in a million chance that the test is wrong!" he thunders, "so he's guilty beyond a reasonable doubt; you must convict."

The problem here—colloquially known as the prosecutor's fallacy—is a misuse of the concept of conditional probability, that is, the probability that something is true given something else.  We write the conditional probability as 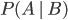P(A\,|\,B), the probability that 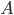A is true if it turns out that 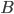B is true.  It turns out that 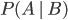P(A\,|\,B) is not the same thing in general as P(B\,|\,A).

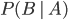When we say that the rate of false positives is 1 in a million, we mean that

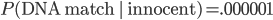
P(\mathrm{DNA\,match}\,|\,\mathrm{innocent}) = .000001

(note that I'm writing probabilities as numbers between 0 and 1, rather than as percentages between 0 and 100).  However, the probability of guilt given a match is not the same concept:

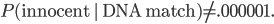
P(\mathrm{innocent}\,|\,\mathrm{DNA\,match}) \neq .000001.

The reason for this error is easy to see.  The police database contains 100,000 names, which is 10% of a million.   That means that even if all 100,000 people are innocent, the odds are still nearly equal to .1 that some poor sucker on the list is going to have a false positive (it's slightly less than .1 actually, because sometimes there are multiple false positives, but I'm going to ignore this since it's a small correction.)

Suppose that there's a .5 chance that the guilty person is on the list, and a .5 chance that he isn't.  Then prior to doing the DNA test, the probability of a person on the list being guilty is only 1 : 200,000.  The positive DNA test makes that person's guilt a million times more likely, but this only increases the odds to 1,000,000 : 200,000 or 5 : 1.  So the suspect is only guilty with 5/6 probability.  That's not beyond a reasonable doubt.  (And that's before considering the possibility of identical twins and other close relatives...)

Things would have been quite different if the police had any other specific evidence that the suspect is guilty.  For example, suppose that the suspect was seen near the scene of the crime 45 minutes before it was committed.  Or suppose that the suspect was the murder victim's boyfriend.  Suppose that the prior odds of such a person doing the murder rises to 1 : 100.  That's weak circumstantial evidence.  But in conjunction with the DNA test, the ratio becomes 1,000,000 : 100, which corresponds to a .9999 probability of guilt.  Intuitively, we think that the circumstantial evidence is weak because it could easily be compatible with innocence.  But if it has the effect of putting the person into a much smaller pool of potential suspects, then in fact it raises the probability of guilt by many orders of magnitude.  Then the DNA evidence clinches the case.

So you have to be careful when using conditional probabilities.  Fortunately, there's a general rule for how to do it.  It's called Bayes' Theorem, and I've already used it implicitly in the example above.  It's a basic result of probability theory which goes like this:

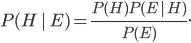
P(H\,|\,E) = \frac{P(H)P(E\,|\,H)}{P(E)}.

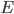The way we read this, is that if we want to know the probability of some hypothesis H given some evidence E which we just observed, we start by asking what was the prior probability P(H) of the hypothesis before taking data.  Then we ask what is the likelihood P(E\,|\,H), if the hypothesis H were true, we'd see the evidence E that we did.  We multiply these two numbers together.

Finally, we divide by the probability 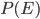P(E) of observing that evidence 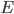E.  This just ensures that the probabilities all add up to 1.  The rule may seem a little simpler if you think in terms of proability ratios for a complete set of mutually exclusive rival hypotheses 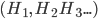(H_1,\,H_2\,H_3...) for explaining the same evidence 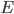E.  The prior probabilities 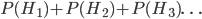P(H_1) + P(H_2) + P(H_3)\ldots all add up to 1.  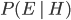P(E\,|\,H) is a number between 0 and 1 which lowers the probability of hypotheses depending on how likely they were to predict 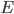E.  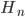If H_n says that 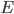E is certain, the probability remains the same; if 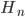H_n says that 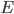E is impossible, it lowers the probability of 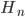H_n to 0; otherwise it is somewhere inbetween.  The resulting probabilities add up to less than 1.  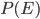P(E) is just the number you have to divide by to make everything add up to 1 again.

If you're comparing two rival hypotheses, 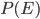P(E) doesn't matter for calculating their relative odds, since it's the same for both of them.  It's easiest to just compare the probability ratios of the rival hypotheses, because then you don't have to figure out what 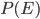P(E) is.  You can always figure it out at the end by requiring everything to add up to 1.

For example, let's say that you have a coin, and you know it's either fair (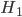H_1), or a double-header 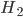H_2.  Double-headed coins are a lot rarer than regular coins, so maybe you'll start out thinking that the odds are 1000 : 1 that it's fair (i.e. 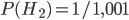P(H_2) = 1/1,001).  You flip it and get heads.  This is twice as likely if it's a double-header, so the odds ratio drops down to 500 : 1 (i.e. 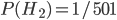P(H_2) = 1/501).  A second heads will make it 250 : 1, and a third will make it 125 : 1 (i.e. 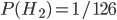P(H_2) = 1/126).  But then you flip a tails and it becomes 1 : 0.

If that's still too complicated, here's an even easier way to think about Bayes' Theorem.  Suppose we imagine making a list of every way that the universe could possibly be.  (Obviously we could never really do this, but at least in some cases we can list every possibility we actually care about, for some particular purpose.)  Each of us has a prior, which tells us how unlikely each possibility is (essentially, this is a measure of how surprised you'd be if that possibility turned out to be true).  Now we learn the results of some measurement 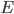E.  Since a complete description of the universe should include what 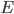E is, the likelihood of measuring 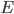E has to be either 0 or 1.  Now we simply eliminate all of the possibilities that we've ruled out, and rescale the probabilities of all the other possibilities so that the odds add to 1.  That's equivalent to Bayes' Theorem.

I would have liked to discuss the philosophical aspects of the Bayesian attitude towards probability theory, but this post is already too long without it!  Some other time, maybe.  In the meantime, try this old discussion here.

Posted in Scientific Method | 4 Comments

All points look the same

by Aron Wall Posted on December 20, 2012

I've told you so far that the gravitational field is encoded in a 4 \times 4 matrix known as the metric.  Here it is, displayed as a nice table:

g_{ab} = \left( \begin{array}{cccc} g_{00} & g_{01} & g_{02} & g_{03}\\ g_{01} & g_{11} & g_{12} & g_{13} \\ g_{02} & g_{12} & g_{22} & g_{23} \\ g_{03} & g_{13} & g_{23} & g_{33} \end{array} \right)

There's 10 components because the matrix is symmetric when reflected diagonally.  The 4 diagonal components (g_{00}, g_{11}, g_{22}, g_{33}) tell you how to measure length-squared along the four coordinate axes.  For example, the length along the 1-axis is given by

\Delta s = \sqrt{g_{11}} \Delta x^1,

where \Delta x^1 is the coordinate difference in the 1-direction.  The remaining 6 off-diagonal terms keep track of the spatial angle between the coordinate axes.  If you know enough Trigonometry, you can figure out that the angle \theta between e.g. the 1-axis and the 2-axis is given by this formula:

\cos(\theta) = \frac{g_{12}} {\sqrt{g_{11} g_{22}}}

However, I've also said that the metric depends on the choice of coordinates, which is arbitrary.  We can use this freedom to choose a set of coordinates where the metric looks particularly simple at any given point.   We can start by choosing our four coordinate axes to be at right-angles to each other.  This gets rid of all those funky off-diagonal components of the metric, which involve two different directions:

g_{ab} = \left( \begin{array}{cccc} g_{00} & 0 & 0 & 0\\ 0 & g_{11} & 0 & 0 \\ 0 & 0 & g_{22} & 0 \\ 0 &0 & 0 & g_{33} \end{array} \right)

If any of the four remaining numbers happen to be 0, we say that the metric is degenerate.  This would correspond to a weird geometry in which you can move in one of the directions for free without it affecting your total distance travelled.  Since we all know that's not the way the real world works, we'll ignore this possibility.

We can also rescale the tick marks along any coordinate axis.  This allows us to multiply each diagonal component of the metric by a positive real number.  So if say g_{22} is positive, we can choose coordinates where it's +1, and if it's negative, we can choose coordinates where it's -1.  This gives us:

g_{ab} = \left( \begin{array}{cccc} \pm 1 & 0 & 0 & 0\\ 0 & \pm 1 & 0 & 0 \\ 0 & 0 & \pm 1 & 0 \\ 0 &0 & 0 & \pm 1 \end{array} \right)

Since it also doesn't matter what order we list the four coordinate directions, all that matters is the total number of +'s and -'s.  This choice is called the signature of the spacetime.

Now if you remember my very first post on spacetime geometry, + directions in the metric correspond to spatial dimensions, while the funny - sign is what makes for a time dimension.  But the real world has one time dimension, everywhere.  No matter how far you travel, you'll never find a place (so far as we know) where there isn't any time direction, or where there are extra time dimensions.  So that means that the correct signature for spacetime has (-, +, +, +) along the diagonal, which is called Lorentzian (a.k.a. Minkowskian) signature.  (If we had wanted to describe a timeless four-dimensional space, we would instead select the Riemannian (a.k.a. Euclidean) signature (+, +, +, +).)  We conclude that for any point of spacetime, you can always choose a set of coordinates such that the metric takes a special form that we'll call \eta_{ab}:

g_{ab} = \left( \begin{array}{cccc}-1 & 0 & 0 & 0\\ 0 & +1 & 0 & 0 \\ 0 & 0 & +1 & 0 \\ 0 &0 & 0 & +1 \end{array} \right) = \eta_{ab}.

In other words, if you zoom in on any point, you recover Special Relativity.  So after all this fidgeting around, we end up with a somewhat profound conclusion: in General Relativity, every point of spacetime looks the same as every other point.

This is related to what Einstein called the Equivalence Principle, which says that at short enough distances, the effects of acceleration are indistinguishable from being in a gravitational field.  We all know from personal experience that riding in an elevator can make us weigh more or less, and from TV that astronomers in the Space Shuttle are weightless when they're in free fall.  In other words, you can always choose a coordinate system in which there is no gravitational force at any given point.

(Lewis Carroll actually described this principle several decades before Einstein in Sylvie and Bruno, which includes a description of a tea party taking place in a freely-falling house.  Then he describes what happens if the house is being pulled down with a rope faster than gravity would accelerate it, and explains how you could have a normal tea party as long as you have it upside-down.  I like this book better than his more famous classics, but don't read it unless you can withstand LD20 of Victorian sentimentality about fairy children.  Also, Carroll didn't go on to discover a revolutionary theory of gravity based on this principle.)

It might seem now like everything has become too simple.  If the metric looks the same at every single point, then why did we even bother with it?  Where's the information in the gravitational field?  Well, it's true that for any one point, there's a coordinate system where the metric looks just like \eta_{ab}.  But there's no coordinate system for which the metric looks like \eta_{ab} everywhere at once.  (Unless there's no gravitational field anywhere, in which case Special Relativity is true).  If you make the metric look simple in one place, it has to look complicated somewhere else.

So in order to describe the gravitational field properly, we have to find a way to compare the metric at different points.  We can do this using something called parallel transport.  I'll give more details later, but basically it tells us how an object moves in a gravitational field when we carry it along a path through spacetime.  When we carry the object around a tiny loop so that it returns to its original position, we might find that it comes back rotated compared to its original orientation.  If so, we say that the spacetime contains curvature.  If the spacetime contains curvature, this is a fact about the gravitational field which is invariant, i.e. objectively true.  You can't eliminate it just by changing your coordinates.

Posted in Physics | 3 Comments

What is NOT Science?

by Aron Wall Posted on December 19, 2012

In my Pillars of Science series, I enumerated six aspects of Science that help explain why it works so well.

It should be clear from my analysis that the characteristics of Science are quite flexible.  All of the criteria are matters of degree, so that they are met more strongly by some fields of study than by others.  Because of this fuzziness, we should expect to find borderline sciences, such as Economics, Anthropology, Psychology, and other social sciences.  It is both futile and unnecessary to try to come up with a criterion to draw an exact line between science and non-science.  In other words, the question of what counts as Science cannot itself be resolved with scientific precision, and is therefore not a scientific question.

This doesn't bother me too much because my parents are linguists.  So when I was growing up, they made sure I was aware that concepts are defined by their centers, not their boundaries.  For example, if I say the word "chair", then what pops into your mind is a thing with four legs at the dinner table.  You might admit under interrogation that a "beanbag chair" is also a chair, but it's hardly the first thing you'll think of.  Concepts can be useful even when they're a bit fuzzy at their boundaries.

Despite their flexibility, the criteria are sufficiently strict that many things don't qualify.  I don't just mean pseudo-sciences such as astrology or homeopathic medicine, but genuine evidence-based fields of knowledge (“sciences” in the archaic sense of the word) which aren't scientific in the modern sense, because they only satisfy some of the criteria.

For example, History and and Courts of Law, despite their empirical character, deal mostly with unique and unrepeatable events.  So they fail the repeatability prong of Pillar I.  Both of these fields are based primarily on testimony of witnesses, although Law Court fact-finding has much stricter rules about admissibility of evidence.  Since much of their subject matter can't be defined with quantitative precision, they don't do terribly well on Pillar IV either.  Academics in History do have a truth-seeking community similar in kind to the Sciences.  But in Law Courts, the role of ethics, community, and authority is completely different.

This does not mean that these fields should be held in contempt; their methods are sometimes capable of establishing specific facts with a very high degree of certainty, “beyond a reasonable doubt” as the saying goes.  They simply lack the particular methodology of science, which has a proven track record of almost routinely proving astonishing facts about the world, to a degree that ends rational opposition.  If you try to increase certainty by imposing a “scientific” approach on a subject that isn't suited for it, you risk generating a pseudo-science which jingles the jargon of science while missing its core value: self-correction through rigorous testing of ideas.

Philosophy is nonscientific for a different reason than the empirical humanities.  While many philosophers strongly value elegance and precision of ideas, typical disputes between philosophers are not very amenable to empirical testing.  That doesn't mean that observation plays no role.  But the way philosophers typically make arguments, they also rely on controversial background assumptions, which can't be definitively settled just by looking at the world.

If, despite the potential for controversy, the argument for the position is sufficiently convincing, this can still establish the philosophical position with great certainty.  In fact, unless the skeptical thesis that no knowledge is reliable could be refuted with near certainty, the result would be that no field of inquiry could produce near certainty.  This potential for certainty does not change the fact that Philosophy operates by a different methodology, which on average does not resolve controversies as easily as the methods of Science or even History do.

For this reason a philosophical thesis based on Science will usually have the degree of certainty associated with Philosophy, not that associated with Science.  A chain of reasoning is only as strong as its weakest link.  So a philosophical argument based on Science should not necessarily trump, e.g. a strong historical argument, simply because Science is normally more reliable than History.

So how do we fit ideas from different fields together?  In a future post, I'll discuss Bayes' Theorem, which is a flexible way to think about all different kinds of evidence-based reasoning, without making specific assumptions about the sorts of evidence we can include.

Posted in Scientific Method | Leave a comment

Pillars of Science: Summary and Questions

by Aron Wall Posted on December 15, 2012

I've now completed my Pillars of Science series.  My goal was to analyze why Science is  such an amazingly effective method for discovering new truths about the world.  Here are the 6 "Pillars" I identified.  Of course, Science is a multifaceted word: it can refer to a method, a set of theories, or a community.  Understanding how Science works really requires thinking about all 3 together.

Intro:

A. How do we test scientific ideas?

B. What kinds of ideas can be tested scientifically?

C. Who can test them effectively?

Having laid this preparatory groundwork, in the next few weeks I'd like to get to a more exciting and controversial topic: I plan to discuss Christianity specifically in the context of each of these 6 Pillars to see how well it holds up.  (But before I get to that, I plan to post a bit about whether there are any other evidence-based ways of looking at the world, besides Science.)

You see, in this blog I am taking seriously the "What about Science?" objection to Christianity.  Many people think that the basic principles of Science are somehow refute or undercut religious views.  These are supposedly based on something called "faith" which is diametrically opposed to "evidence".  While everyone knows that some scientists are religious, many people think this is only possible because of "compartmentalized thinking" in which the two different approaches to life are somehow sealed off in different compartments so that the "evidence" compartment isn't allowed to explode the "faith" compartment.

Now those of us who practice the spiritual discipline of Undivided Looking obviously approve of UN-compartmentalized thinking, in which we think of reality as a whole, without making special exemptions for parts of life we don't want to subject to critical scrutiny.  Somewhat paradoxically, this does not require us to disapprove of compartmentalized thinking.  In certain respects Science itself is based on compartmentalized thinking (see Pillar III).

And we couldn't stop doing it even if we tried, because our brains are wired for compartmentalized thinking.  (Especially the male brain, which is more likely to delegate tasks to particular regions of the brain, whereas the female brain is more likely to think using connections between different parts of the brain.  See e.g. this study.)  But what we can and should do sometimes, is make a conscious effort to look at things together, rather than separately.

Since I'm going to be referring back to these six Pillars of Science, I'd like to ask for some reader feedback.  Do you think my discussion of these Pillars could be improved?  I'd like to solicit criticisms on any of the following issues, or anything else you can think of:

  • Is there any practice which is important to Science which I have not included in the Pillars?  Or which I should have emphasized more?
  • Is there anything which I've said is important for Science, which actually isn't?  Are there branches of Science which do without any of these things?
  • My perspective is that of a physicist who works on fundamental issues.  But there's lots of other scientific fields: Biology, Geology, Chemistry, etc.  Do you think someone from these fields might have prioritized different aspects of scientific practice than I did?
Posted in Scientific Method | 38 Comments

Coordinates don't matter

by Aron Wall Posted on December 12, 2012

In my last post about spacetime, I explained how the geometry of spacetime is determined at each spacetime point by a set of 10 numbers.  These 10 numbers are packaged together into a 4 \times 4 matrix called the metric, which is written as g_{ab}.  The subscripts a and b stand in for any of the 4 coordinate directions (in a 4-dimensional spacetime).  Since the metric is symmetric, i.e. g_{ab} = g_{ba}, there are 10 possible numbers in this matrix.  The value of these 10 numbers depends on your position and time,which makes them a field, specifically the gravitational field.

However, there is an important caveat in all this.  The coordinates which you use to describe a given spacetime are totally arbitrary.  For example, a flat 2-dimensional Euclidean plane can be described using Cartesian coordinates -\infty < x < +\infty and -\infty < y < +\infty.  In this coordinate system, the distance-squared is given by the Pythagorean formula

(ds)^2 = (dx)^2 + (dy)^2,

which can be written in terms of the metric as

g_{xx} = 1; \qquad g_{yy} = 1; \qquad g_{xy} = 0.

On the other hand, for applications involving rotations, it's often useful to use polar coordinates: 0 \le r < +\infty (the distance from the origin) and 0 \le \theta < 2\pi (the angle around the origin, measured in radians).  They're related to the original coordinate system by

x = r \sin \theta;\\ y = r \cos \theta.

  In polar coordinates, the distance-squared is given by

(ds)^2 = (dr)^2 + r^2 (d\theta)^2,

where the extra r^2 factor comes in because circles that are a greater distance from the origin have a larger circumference, so there's more space as you move outwards.  This can be written in terms of the metric like this:

g_{rr} = 1; \qquad g_{\theta\theta} = r^2; \qquad g_{r\theta} = 0.

(Note: I've given these coordinate systems their traditional coordinate names to make them look more familiar, but this is actually just a redundancy to make it easier for humans to think about it.  I could have written the two coordinates as (x^0, x^1)—the superscript being a coordinate index, not an exponent—and then you could tell whether it was Cartesian or polar coordinates just by inspecting the formula for the metric.)

Now the point is, these two coordinate systems describe the same geometry in a different coordinate system.  If we were playing pool (or billiards) on a planar surface, and you wanted to describe how billiard balls bounce off of each other, you could equally well describe it using either coordinate system.  The physics would be the same.

Of course, the language you use to describe the system differs.  Suppose that I analyze a collision using Cartesian coordinates, while you use polar coordinates.  And suppose we had to communicate to each other what happened.  If you say to me, "The cue ball had a velocity in the x^1 direction", then I'll get confused because x^1 means something different to me than it does to you.  These kind of statements vary under a change of coordinate system, they are "relative" to your coordinate-perspective.  So if you want to communicate with me, you have to find a way to describe what's going on which does not refer to coordinates in any way.  For example, you could say "The cue ball hit the 3 ball, which knocked the 8 ball into a pocket."  Since the two balls and the pocket are unique physical objects, we can all agree on whether or not this happened, no matter what coordinate system we use.  These kind of statements are invariant under a change of coordinate system.  The goal of coordinate-invariant physics is to describe everything in this sort of way.

Here's another way in which coordinate systems can let you down: when you use polar coordinates, there are places where the coordinates go kind of funny.  For example, when you're going around the origin clockwise in the direction of increasing \theta, and you arrive at \theta = 2\pi, you immediately teleport back to \theta = 0 since you've come full circle.  Even stranger, space seems to come to an end at r = 0 (the origin) since there's no such thing as negative r.  And if you're sitting right at r = 0, the different values of \theta all refer to the same point as each other.  However, in reality we know that nothing weird is happening to the geometry at any of these points, since nothing strange happens in Cartesian coordinates.  (A similar issue comes up in black hole physics.  The original set of coordinates found by Schwarzschild blow up at the event horizon, but actually nothing unusual happens there in classical general relativity.)

The upshot of all this for general relativity is the following: I told you above that you can describe general relativity using the metric g_{ab}, which involves 10 numbers at each point.  But this description actually has some redundancy in it, since there's infinitely many possible coordinates systems you could use (one for each way of labelling the points uniquely with four numbers), and the metric looks different in each one—it isn't an invariant object.

When a theory has redundancy like this, we say there is a gauge symmetry.  A regular symmetry says that two different states (i.e. configurations) of a system behave in the exact same way as each other.  A gauge symmetry is stronger than a regular symmetry: it says that the two configurations are actually the same physical state of affairs.  In general relativity, the choice of coordinates is a gauge-symmetry.  It is a mere human convention which doesn't correspond to any actual physical thing in Nature.

Of course, even if you aren't doing general relativity, you can still use whatever coordinate system you like!  Most games of billiards can be understood in the approximation where space is flat (unless you like to spice up your games with black holes and gravity waves, like the cool kids do!)  In flat space time, all coordinates are equal, but some are more equal than others.  Although nothing stops you from calculating in horrible coordinates, the laws of physics look especially simple in ordinary Minkowski coordinates, where the symmetries of spacetime look especially simple.  Since Newton's First Law of motion holds in these coordinates, we call it an inertial frame.  (Here I'm ignoring the downward pull of gravity, since in billards we're only interested in horizontal motions.)

However, if you're doing general relativity, then there's a property of spacetime which forces you to describe physics in a coordinate-invariant way; at least if you want the equations of the theory to look elegant and lovely instead of like horrendous cludge.  This property is called curvature—but we're out of time for today.

Posted in Physics | Leave a comment