There's been a huge kerfuffle in the quantum gravity community since this summer, when some people here at UCSB published a paper arguing that (old enough) black holes may actually be surrounded by a wall of fire which burns people up when they cross the event horizon. This is huge, because if it were true it would upset everything we thought we knew about black holes.
General relativity is our best theory of gravity to date, discovered by Einstein. This is a classical theory. (In the secret code that we physicists use, classical is our code-word for "doesn't take into account quantum mechanics". Don't tell anyone I told you.)
In my other posts on physics, I've been trying to explain the fundamentals of physics in the minimum number of blog posts. This post is out of sequence, since I haven't described general relativity yet! But I wanted to say something about exciting current events.
In classical general relativity, a black hole is a region of space where the gravity is so strong that not even light can escape. They tend to form at the center of galaxies, and from the collapse of sufficiently large stars when they run out of fuel to hold them up. A black hole has an event horizon, which is the surface beyond which if you fall in, you can't ever escape without travelling faster than light. The information of anything falling into the black hole is lost forever, at least in classical physics.
In the case of a non-rotating black hole, without anything falling into it, the event horizon is a perfect sphere. (If the black hole is rotating, it bulges out at the equator.) If you fall past the event horizon, you will inevitably fall towards the center, just as in ordinary places you inevitably move towards the future.
At the center is the singularity. As you approach the singularity, you get stretched out infinitely in one direction of space, and squashed to zero size in the other two directions of space, and then at the singularity time comes to an end! Actually, just before time comes to an end, we know that the theory is wrong, since things get compressed to such tiny distances that we really ought to take quantum mechanics into account. Since we don't have a satisfactory theory of quantum gravity yet, we don't really know for sure what happens.
Now it's important to realize that the event horizon is not a physical object. Nothing strange happens there. It's just an imaginary line between the place where you can get out by accelerating really hard, and the place where you can never get out. Someone falling into the black hole just sees a vacuum. If the black hole was formed from the collapse of a star, the matter from the star quickly falls into the singularity and disappears. The black hole is empty inside, except for the gravitational field itself.
We don't know how to describe full-blown quantum gravity, but we have something called semiclassical gravity which is supposed to work well when the gravitational effects of the quantum fields are small. In semiclassical gravity, one finds that black holes slowly lose energy from thermal "Hawking" radiation. This radiation looks exactly like the random "blackbody radiation" coming from an ordinary object when you heat it up. Here's the important fact: You can prove that the radiation is thermal (i.e. random) just using the fact that someone falling across the horizon sees a vacuum (i.e. empty space) there.
The Hawking radiation comes from just outside the event horizon. It does not come from inside the black hole, so in Hawking's original calculation it doesn't carry any information out from the inside. Nevertheless, for various reasons I can't go into right now, most black hole physicists have convinced themselves that the information eventually does come out.
As the black hole radiates into space, it slowly evaporates, and eventually probably disappears entirely (although knowing what happens at the very end requires full-blown quantum gravity). If the outgoing Hawking radiation carries all the radiation out, then for a black hole at a late enough stage in its evaporation, the radiation must not be completely random, because it actually encodes all the information about what fell in.
The gist of what Almheiri, Marolf, Polchinski, and Sully argued, is that if we take both of these statements in bold seriously, then it follows that the black holes are NOT in the vacuum state from the perspective of someone who falls in. Instead you would get incinerated by a "firewall" as you cross the horizon. (It's not clear yet whether this is only for really old black holes, or if it applies to younger ones too.) That's if we still believe there is an "inside" at all. The argument shows that semiclassical gravity is completely wrong in situations where we would have expected it to work great.
If this is right, then it's devastating to the ideas of many of us who have been thinking about black holes for a long time. As a reluctant convert to the idea that information is not lost, I'm wondering if I should reconsider. At the end of this month, I'm going to Stanford for a weekend, since Lenny Susskind has invited a bunch of us to try to get this worked out. Exciting times!

that's so great that you're invited to work on such an interesting problem with Leonard Susskind!! I find his lectures on youtube to be very instructive...
But anyway I have a physics question. What in the theory determines whether someone falling into a black hole would see a vacuum or a firewall? What's the debate, whether the black hole is in the vacuum state or not? I can't see why anyone crossing the event horizon would "see a vacuum"; as long as other stuff is falling in (which is generally true for galactic black holes, anyway); wouldn't light from other stuff falling in still reach you as you fall in with it? Is it that stuff falling in that would create the firewall, or is the firewall from the Hawking radiation, or something else? I guess that was more than one question :)
Good questions, Luke.
You're quite right that if other stuff is falling into the black hole along with you, then you don't see a vacuum state. However, that's not important since we can consider a hypothetical situation in which no stuff is falling in from outside, except you. The AMPS argument says there should be a firewall even then. (Alternatively, if stuff is falling in, we could just ask about really short distance sclaes, since in quantum field theory all states look like the vacuum at sufficiently short distances.)
Since the stuff falling in is in the vacuum state, the question really concerns the fields travelling outwards near the horizon. (If the outgoing modes are just outside the event horizon, they can escape as Hawking radiation, while if they are just inside, even the "outgoing" modes, which are trying to escape, get inexorably sucked in.) These are the modes that AMPS say have to be in a non-vacuum state.
Quantum field theory says that if you take a vacuum state, and restrict your attention to one side of a plane dividing space into two halves, then the fields outside the plane are in a thermal state, including quanta of arbitrarily high energies. However, these thermal fields just outside are quantum mechanically entangled with the fields just inside. The reason you don't get burnt to a crisp whenever you cross the door to your bedroom, is that the adverse effects of the fields just outside are almost exactly cancelled out by the effects of the fields just inside. In semiclassical gravity, the exact same story applies for an infalling observer crossing the event horizon.
The AMPS argument says that if black holes don't permanently lose information, then as time passes, this exact cancellation must eventually break down. Technically speaking, that's because the Hawking radiation at late times can't be simultaneously quantum mechanically entangled with both the radiation inside the event horizon, and the radiation emitted at earlier times.
You ask what in "the theory" determines whether you see a vacuum or the firewall. If the theory is general relativity, or semiclassical gravity, the answer is that you see a vacuum, not a firewall. If the theory is quantum gravity, then AMPS claim that given certain assumptions, logical consistency requires that there be a firewall. However, we don't know what the mechanism would be, since we don't even know how to formulate the theory!
Why did you (once) think that information is lost?
Mitchell,
Because that's what happens in semiclassical general relativity: the Hawking radiation is completely uncorrelated with anything that fell in. One expects that quantum gravity effects should only make a difference when the amount of spacetime curvature is large. Curvatures are large at the singularity, but not near the event horizon.
Also, it seems like the information could only escape from the singularity if the laws of physics are nonlocal. Since general relativity and quantum field theory are each local (in the relevant sense), this seemed implausible.
I was convinced that the information does come out by a very simple argument by Don Marolf, here at UC Santa Barbara. The basic idea is that in general relativity, the mass (= energy) of a system is measurable at spatial infinity, because of the long-range nature of the gravitational field. For example, you could put a planet in orbit around the system and measure the gravitational mass that way.
But in quantum mechanics, if you can measure the energy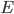 and some other observable
and some other observable 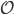 , you can also measure the same observable
, you can also measure the same observable 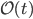 at any past or future time. (For those who want to see the math, the formula is
at any past or future time. (For those who want to see the math, the formula is 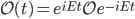 .) That means that if you create an object very far from the black hole, and then drop it into the black hole, the information must still be encoded somehow in the information at infinity. This is related to something called the "holographic principle".
.) That means that if you create an object very far from the black hole, and then drop it into the black hole, the information must still be encoded somehow in the information at infinity. This is related to something called the "holographic principle".
Pingback: East Coast versus West Coast | Not Even Wrong
Unless you can test it. Who cares.
Math models are usually just approximations to reality, so all this brain twisting logic may not correspond to it anyways.
Or if there is a dual between Black Holes and super conducting physics, maybe you can device a test. Oh and yes there are some duals from ST math, so go to it.
Sorry for the late reply, but this whole black hole information thing confuses me. (A lot of things confuse me, which is why I'm reading thru the archives from the start)
What about a closed/finite universe where there is no infinity to measure things at, and the total mass/energy is always zero?
Also, would information still be conserved in that way on an objective collapse theory?
David,
Rule 1 says you can leave comments as if the posts were written yesterday. So I demand that you take your apology back! :-)
Also, the black hole information puzzle confuses everyone, so you're in good company.
Don Marolf's argument only applies if the universe has an asympototic boundary at infinity. In fact it works best if it's asymptotically Anti-de Sitter spacetime, which is the vacuum state associated with a negative cosmological constant. (In our universe, the cosmological constant seems to be positive.) Nevertheless, I suspect that whether or not black holes lose information shouldn't depend on the details of what's going on at infinity (or whether there even is an infinity). This is just a personal intuition but I'd justify it as follows: (a) infinity has to do with really big stuff that's far away, but this shouldn't make a difference to the behavior of a small black hole, and (b) the laws of horizon thermodynamics seem to be pretty similar regardless, and presumably this is related to the information puzzle.
Information would not still be conserved in an objective collapse theory. This seems somewhat analogous to black hole physics if the information is lost. In both cases you would start with a "pure state" (i.e. a quantum superposition of states) and end up with a "mixed state" (i.e. a classical probability distribution over a set of states). In standard quantum mechanics, there is a way of describing mixed states (called "density matrices") but there is no way for a pure state to become a mixed state by unitary evolution (as in a closed system).
So you might wonder if the two phenomena (collapse and black holes) are connected somehow. But most people in the field don't take objective collapse theories very seriously, partly because it is very difficult to formulate them in a way which is relativistically covariant and satisfies other desirable properties. The problem is serious enough that people are making proposals which are tantamount to violating the linearity of QM, so perhaps all options should be on the table. Yet mostly in my own work I assume that QM remains linear and try to work out its implications, out of a possibly misguided sense of conservativism...
Is there a canonical theory of Information that we can use to clarify out thinking about what exactly we mean by "information"?