Science requires Approximations.
Every kind of professional activity changes the way you think. It rewires your brain so that even when you're off the job, things start looking a certain way. For example, to a computer programmer everything looks like an algorithm. To a teacher, everything is pedagogical. As a physicist, what goes through my head every day is approximations.
Every time I think about a situation involving black holes, or prove a theorem, or do a calculation, I always have to keep in the back of my mind what kinds of physical effects I'm ignoring, not taking into account. This habit has leaked out into my thinking about life in general. Ideas don't have to be just true or false, instead they can be good approximations in some contexts, and bad approximations in other contexts.
(Partly related: before I started doing physics seriously, I think I had the idea in the back of my head that when I went to grad school, I'd learn how to calculate the really hard problems. But it turns out there is no way to calculate the answers to the hard math problems. There are only clever tricks for simplifying hard problems so that they become easy problems. Frequently, the clever trick is finding some parameter that can be taken to be small, in order to justify some approximation. The way this works is: first you figure out what happens if the parameter is zero, and then you calculate the tiny effects of it not quite being zero.)
It is impossible for any model of the universe to capture every feature of reality, or else it would be too complicated for human beings to analyze, or to compare to experiment, at the high level of precision demanded by science. Consequently every scientific theory is applicable only to some limited range of phenomena. In other words, it isolates some feature of reality which is as free as possible from contaminating influences, and which is simple enough to be either measured experimentally or calculated theoretically (ideally, one can do both, to compare the theory to the experiment).
Therefore, Science consists of a bunch of partly overlapping models which cover different patches of reality. Some of these patches are smaller, and cover very specific situations (e.g. Bernoulli's principle for fluid dynamics) and others cover a very broad range of situations (e.g. Quantum Electrodynamics, which covers everything related to electricity, chemistry, and light). None of these patches covers everything, and the two broadest patches, Quantum Field Theory and General Relativity, cannot yet be fully reconciled with one another.
One of the implications of this principle is that scientific revolutions seldom result in the complete discrediting of the old well-established theory. The reason is that if the first theory explained a significant patch of data, the new theory can only supercede the old one if it explains all the things the first one explained, and more. Usually this means that the old theory is a limiting situation or special case of the new theory. Thus the old theory is still valid, just in a smaller patch than the new theory. For example, Einstein's theory of General Relativity superceded Newton's theory of gravity, but it predicts nearly the same results as Newton in the special case that the objects being considered are travelling much slower than light, and their gravitational fields are not too strong.
Thus the empirical predictions of Newton's theory are still correct when applied in the proper domain. However, the philosophical implications regarding the nature of space and time could hardly be more different in the two theories, because the Newtonian theory regards space and time as fixed, immutable, separate entities, while Einsteinian theory regards spacetime as a single contingent field capable of being affected by the flow of energy and momentum through the spacetime.
Philosophers who reason from scientific discoveries should take warning from this: although the empirical predictions of a theory usually survive revolution, the philosophical implications often do not. Thus our current scientific views on such matters should be taken as somewhat provisional. On the other hand, it would be even more foolhardy to try to discuss the philosophical nature of space, time, causality, etc. without taking into account the radical changes which Science has made to our naïve intuitions about these concepts. Some improvement of our thinking is better than none.

"One of the implications of this principle is that scientific revolutions seldom result in the complete discrediting of the old well-established theory." So, when the accepted theory was that the world was flat, did declaring that it was in fact round not completely discredit that theory? What portion of that theory was not discredited?
Oh spoot - I should have read ahead I guess! Count me with the misinformed who didn't know that wasn't what "they" thought - at least, not the scientists that would have called it a theory! I'm guessing the common man wasn't as knowlegeable...
Leaving aside what the Medievals thought, there actually is a sense in which a flat Earth is a good approximation to a spherical Earth. Namely, if you pick any part of a spherical globe, and imagine zooming in so that you're looking at much smaller distances than the radius of the Earth, then near that point the world does look nearly flat on average (ignoring mountains and valleys and things).
However, there's lots of other examples (besides the shape of the Earth) where people before modern times were just plain wrong about how things worked. For example, the idea that there are unicorns whose horns neutralize poison. (In fact, there are still people who believe wrongly that rhino horns have curative properties.) My point only applies to ideas which have been extensively tested through scientific experiments, and proven to work. In that case, even if the theory is wrong, it can't just be a total coincidence that it predicted things so well. The usual way this works is that it is an approximation to a better theory, and in that sense it is still "true", but only in certain situations.
That almost feels like cheating though -- "Well, I was right IN THIS WAY...so you're still wrong!" kind of defense from the playground...but I do understand your point. The problem is that the non-scientific receivers of the Pronouncements of Science want them to be RIGHT, and not just right, but ALWAYS right (Sorry about the all caps, but I don't seema able to use italics or underscores here?) So they (the public) get really mad when Science comes back and says, "We were right, but now we're right just a little bit differently than we said before (but we're not really wrong, and you can still trust us...)"
Right. That's why I think it's important that scientists warn people in advance about the provisional nature of scientific truth, before the new theory comes along...
If you want to use italics, you can do it by putting html tags before and after what you want to italicize. You do it like this: [i]this phrase will be in italics[/i], only instead of using square-brackets [], you have to use angle brackets <>. I couldn't write it out for you directly, since otherwise it would have looked like this: this phrase will be in italics!
I don't suppose you'll be writing many equations in your comments, but people who know LaTeX can do so by putting a pair of dollar signs both before and after a LaTeX expression, like this: $E = mc^2$ ---(add an extra dollar on each side)--->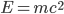 .
.
This exchange reminds me a bit of the account attributed (in the first episode of James Burke’s “The Day the Universe Changed”) to Wittgenstein, the essence of which is that a person once commented to the philosopher, “What fools people must have been to watch the sunrise every day and think it was the Sun going ‘round the Earth, when as any school child knows, it is actually caused by Earth’s rotation in solar orbit.” Wittgenstein replied, “Maybe, but I wonder what it would have looked like if the Sun really had been going ‘round the Earth.”
Of course, to Sherlock Holmes it didn’t make any difference…