I've now completed my Pillars of Science series. My goal was to analyze why Science is such an amazingly effective method for discovering new truths about the world. Here are the 6 "Pillars" I identified. Of course, Science is a multifaceted word: it can refer to a method, a set of theories, or a community. Understanding how Science works really requires thinking about all 3 together.
Intro:
A. How do we test scientific ideas?
B. What kinds of ideas can be tested scientifically?
C. Who can test them effectively?
Having laid this preparatory groundwork, in the next few weeks I'd like to get to a more exciting and controversial topic: I plan to discuss Christianity specifically in the context of each of these 6 Pillars to see how well it holds up. (But before I get to that, I plan to post a bit about whether there are any other evidence-based ways of looking at the world, besides Science.)
You see, in this blog I am taking seriously the "What about Science?" objection to Christianity. Many people think that the basic principles of Science are somehow refute or undercut religious views. These are supposedly based on something called "faith" which is diametrically opposed to "evidence". While everyone knows that some scientists are religious, many people think this is only possible because of "compartmentalized thinking" in which the two different approaches to life are somehow sealed off in different compartments so that the "evidence" compartment isn't allowed to explode the "faith" compartment.
Now those of us who practice the spiritual discipline of Undivided Looking obviously approve of UN-compartmentalized thinking, in which we think of reality as a whole, without making special exemptions for parts of life we don't want to subject to critical scrutiny. Somewhat paradoxically, this does not require us to disapprove of compartmentalized thinking. In certain respects Science itself is based on compartmentalized thinking (see Pillar III).
And we couldn't stop doing it even if we tried, because our brains are wired for compartmentalized thinking. (Especially the male brain, which is more likely to delegate tasks to particular regions of the brain, whereas the female brain is more likely to think using connections between different parts of the brain. See e.g. this study.) But what we can and should do sometimes, is make a conscious effort to look at things together, rather than separately.
Since I'm going to be referring back to these six Pillars of Science, I'd like to ask for some reader feedback. Do you think my discussion of these Pillars could be improved? I'd like to solicit criticisms on any of the following issues, or anything else you can think of:
- Is there any practice which is important to Science which I have not included in the Pillars? Or which I should have emphasized more?
- Is there anything which I've said is important for Science, which actually isn't? Are there branches of Science which do without any of these things?
- My perspective is that of a physicist who works on fundamental issues. But there's lots of other scientific fields: Biology, Geology, Chemistry, etc. Do you think someone from these fields might have prioritized different aspects of scientific practice than I did?
You don't mention Bayes' theorem or Bayesian reasoning at any point. That's at the center of why science works, and also at the center of the advanced rationalist's near-instant dismissal of any religious claim. You should address that if you want to engage with the higher-level atheists.
Thanks for your comment, James.
As a matter of fact, I'm a devout Bayesian, just like you, and I was already planning to make a post about it before you asked.
I didn't explicitly say "Bayes' Theorem" yet, but it's there implicitly, under the hood. Pillar II has to do with prior probabilities, and Pillar I has to do with updating based on evidence.)
The reason I didn't mantion Bayes' Theorem explicitly is that it tells us how to engage in evidential reasoning about everything, including History, Philosophy, etc. Whereas the Pillars of Science series is about why scientific fields like Physics, Chemistry, Biology etc. work so well specifically as compared to other evidence-based forms of thinking. Bayes' Theorem isn't the sole explanation, since it can be applied everywhere, not just to Science.
Bayes' Theorem can't possibly lead to an "near-instant dismissal of any religious claim" since it's a framework for analyzing arguments, not an argument all by itself. Unless you start by assigning a zero prior probability to religious claims (and you shouldn't), you have to actually think about the relevant arguments to decide what's true. Bayes' Theorem is helpful for analyzing the structure of arguments to see if they work or not, but it doesn't tell you all by itself what the prior probabilities and the likelihood ratios are.
I didn't say that Bayes' theorem is, all by itself, sufficient reason to do anything, besides maybe follow Bayes' theorem. It is the rule someone should be following when they try to figure out P(this person's religious claims are true | all the evidence this person has presented for specifically their religion).
I eagerly await your explanation of why Christianity has a much higher prior probability for being true than any other religion.
Also, I'd argue that you should be talking Bayesian reasoning precisely because it's more general. Science is a social institution more than anything else, messy and imperfect; Bayesian reasoning is extremely well-defined and promises to always give you a correct (if computationally expensive) answer, whether you call whatever you're applying it to "biology" or "marketing" or "theology".
I totally agree that Bayesian reasoning is a better way to deal with these questions! Although I don't think it promises to give the correct answer, unless we can all agree on the correct rule for constructing priors. I don't think there are any hard and fast rules for "objectively correct" priors, although there are a number of very helpful rules of thumb.
However, there are a lot of people out there who think that there is a conflict between "Science" and Religion, where "Science" means not rationality in general, but some methodology or conclusion related specifically to what people do in Science Departments at a research university. (This is in contrast to the old definition of "Science", which just meant any kind of knowledge.) I want to discuss this in detail since it's such a common view, and because I think I have some interesting things to say about it.
And even though Science in this narrower sense is messy and imperfect, precisely for that reason it may be able to tell us something valuable about how messy and imperfect people can arrive at the truth.
It's nice of you to eagerly await my future posts arguing that Christianity has a much higher prior probability for being true than any other religion. Alas to disappoint you, but I am actually only going to be arguing that Christianity has a higher posterior probability compared to other religions! (I assume that's what you meant to say.)
The same degree of belief can be both a posterior and a prior. If you were born with no knowledge of any religions then learned whatever it is you learned that convinced you Christianity is basically correct with probability -> 1, your resulting degree of belief in Christianity is a posterior, viewed within that context. Then, if you learn something new and relevant to that belief right now, that same degree of belief becomes your prior probability for the next update. From the perspective of the present, I'd call your and my current beliefs "priors", but it's not a terribly important distinction.
I wasn't implying anything about objectivity when I used the word "correct". I meant something more like "Bayes' theorem tells you what you should believe, given the imperfect knowledge you have about the world, and the greater the difference between what you end up believing and what Bayes' theorem says you should believe, the less effectively you'll be able to interact with the world."
I think your prior for Christianity is extremely relevant.
Take just a single feature, the Resurrection. I don't know what the background rate for these sorts of events is, but it's at least rarer than 1 out of a billion deaths. In order to believe that it occurred, you either need to show why this naive prior is wrong, or you need to have mountains and mountains of evidence.
...and then when you consider that Christianity is actually a conjunction of many unlikely claims it becomes hard to imagine how one could possibly accumulate enough evidence to overcome this prior unlikelihood.
Yes, it is. The important question is whether it's reasonable to take the prior so low that it's basically impossible to be convinced by historical evidence.
I don't think that's the right way to do the probability analysis, or at least you have to be very careful about what you mean. The background rate for someone winning the lottery is quite low, yet we don't disbelieve the news reports when they say that some random dude just won the lottery. That's because the tiny prior probability of a specific person winning the lottery is cancelled by an equally enormous likelihood ratio coming from testimony. This cancellation occurs partly because the odds of the news lying about a specific name are quite low.
The fact is that testimony routinely increases the probability of events by many orders of magnitude. If a friend called you and said that their house was on fire, you'd probably believe them even though the odds of it happening in a given day is fairly small.
You're being quite reasonable elsewhere, so I have to give you a hard time about this. Your prior should have nothing to do with what you want or don't want to actually be the case. I picked 1-in-a-billion to be charitable. I think, if I were a christian, I would have to pick something more like 1-in-a-quadrillion to feel that I'd not built my own bias into the question. The point is to make sure that you're not experiencing motivated cognition.
If the best estimate of a prior makes it impossible to be convinced by the evidence, that is god's fault, not yours. You certainly shouldn't be adjusting your best estimate of the prior to make it possible to believe what you want to believe!! This is rational thinking 101! If god wants followers but leaves insufficient evidence to cause rational humans to believe in him/her/it, that's equivalent to saying that he/she/it desires irrational followers!
Imagine an Islamic person following the same mental algorithm you are using. Is it going to reliably turn them into a Christian, or will it cause them to stay Islamic? (Keep in mind that every time you think "bible" they think "koran" and when you think "god" they think "allah"!) If the mental algorithm that you are using doesn't cause moslems to stop being moslems, then why would you expect it to cause you to believe true things?
Second, on lotteries. I did indeed forget that there have been many deaths and therefore the binomial theorem applies. Given the number of people playing and the number of lotteries held, P(someone won the lottery) is not that tiny, so it doesn't take that much evidence to get me to believe it. Likewise, if the true rate of resurrections was 1e-9, there's probably been enough deaths that we would expect a significant chance of a single person having risen (I can't find a binomial calculator online in 30 seconds that will accept numbers large enough, grr). If this were the only feature christianity required, then this argument might go in your favor.
However, this same person that is supposed to have risen from the dead is also supposed to have been born to a virgin. Some animals can actually do this, so I find it much more probable than rising from the dead. Still, it's not been observed in humans, so let's call it 1-in-100-million (which implies there should be three such people living in the US, but I'm being charitable here). But now we're talking about a particular individual, not just anyone in general, so the binomial theorem can't help you. (Or you can run the binomial math with P = 1e-17, it should come out the same either way?) This is like someone winning the lottery while simultaneously inventing FTL space travel.
This is just two features, and you have an entire book which is a conjunction of unlikely claims. The prior for christianity, even given extremely charitable assumptions, is astronomically low!
Oh, I got so excited I forgot to respond to this. I don't necessarily agree. Humans lie at some rate. Humans are mistaken about what they perceive at some rate. Humans perceive correctly, but apply an invalid interpretation at some rate. Humans exaggerate at some large rate. Sometimes the testimony of separate individuals is independent and sometimes it's not. All of this places an upper bound on how accurate testimony can be. I'm going to have a hard time accepting more than 100-1 likelihood ratios from any individual human source. That's not many orders of magnitude.
The reason we don't disbelieve the paper when it says so-and-so won the lottery is because it's not surprising that someone we don't know won the lottery, not that the paper is so trustworthy. I've personally never had the experience of reading/watching/hearing some mass media source on something I know something about and having been impressed by their accuracy. I'm guessing that you haven't, either, given your field is even harder to describe correctly than mine (software/computer science). :)
lavalamp, I think Aron is at least kinda right about testimony. Consider the following example. I could tell you 30 separate facts about my wife, each of which is (independently) true of, say, 10% of the population, and unless you had particular cause to think I was likely lying to you you'd probably believe me. Or maybe believe something like "at most one of these propositions is wrong". Even though, in the absence of my testimony, you'd have estimated something like a 10^-20 probability of there being any living person matching the description, and 10^-18 of there being anyone who fits all but one of the facts.
Christianity is indeed monstrously improbable a priori just because it's (roughly) the conjunction of so many claims, and if Aron denies that then he's very wrong. But the fact that Christianity in all its specificity is something lots of people believe could in principle let it get a lot of that probability back. Working out whether it does, and how much if so, requires something beyond just computing numbers like the ones above: you need to consider the possible ways in which lists of claims like those that (kinda) constitute Christian belief come into existence and get spread, etc.
I think the answer turns out to be of the following form: Pr(Christianity|testimony) is indeed not all that small, but it's quite "soft" because it doesn't take much other stuff for Pr(Christianity|testimony, other stuff) to get very small again. Whether that's actually a good way to put it depends on exactly what you consider part of your background knowledge.
I think I see what you're saying-- we need to give some probability back for each feature individually. So if books like the bible (koran, vedas, book of mormon, etc) are wrong 1/100 times, then for each feature we should do something like add 1e2 to the base rate. At least this is how my brain explained not being surprised at your claims about your wife. After you've told me 100 different things about your wife, I'll believe there's a good chance one of them was wrong or misleading. Because most of the things you say will probably have base rates much higher than 1e-2.
...If you tell me that your wife has an IQ of 170, has cured some type of cancer, has climbed Mt. Everest, and has written one of the amendments to the constitution, well, I'll probably require more evidence than just your say-so.
(Really, we should do this with log-odds, and then the "add 1e2" step is actually a Bayesian update.)
Anyway, good point; sadly, I don't think this is going to give back anywhere near enough probability to help out the theist.
You are quite correct that an idealized Bayesian reasoner would start by calculating the prior odds of a proposition, and that the evidence they receive later can't affect their prior odds. So if you have a good reason to set the prior odds of Christianity at some particular low value, and it turns out that no reasonable amount of historical evidence can make up the difference; then yes, one isn't allowed to whine that probability theory isn't being fair. Note that I said "The important question is whether...", not "It must necessarily be the case that..."
But we are not all idealized Bayesian reasoners. When we set our prior odds there is a danger of bias, as you point out. (I'm pretty sure that idealized Bayesian reasoners also don't add 6 orders of magnitude to the implausibility of a proposition just in case they might be biased by their upbringing, as you suggest nonidealized people should do.) So if someone were to confidently announce that there was a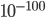
prior probability that God exists (as no one has done here), it's perfectly reasonable as a rhetorical strategy to say something like "Really?!? You're saying that if you personally witnessed [this-fantastically-good-evidence] and [some-other-piece-of-amazing-data] you still wouldn't believe it, even if it were repeated 3 times? Are you sure?"
The point of this rhetorical strategy is not that prior probabilities should depend on what evidence is actually available, but rather to help in estimating the prior probabilities to begin with. You can think of priors as another way of taking about how much evidence it would take to convince you, so one way of asking how low your priors should be is to ask what general kind of evidence might persuade you. This whole process can take place a priori before looking at the actual data for the specific claim.
If in general you feel like beliefs based on empirical data are more reliable than beliefs based on armchair speculation (and you should believe this), then translated into Bayesian terms this is the same as saying that your priors should be fairly "flat", meaning that they don't assign super-low probabilities to unspecific claims without good reason.
Sorry, this isn't the way that Bayesian probability analysis works. If Christianity is true, it's not a coincidence that the same person was both born of a virgin and rose from the dead. That person was special, and there was a common causal factor involved.
You're making a classic mistake, which is to estimate the conditional probability of a miracle occuring given Naturalism and then confuse that with the prior probability of Christianity. If Christianity is true, then the odds of naturalistically implausible events occurring is much higher (because they can happen as miracles when God wants to make a point.) The prior probability for Christianity should be based on the underlying causal postulates of the supernatural hypothesis, e.g. the existence of a God of a particular sort, etc.
For this reason, it's irrelevant that there is naturally occurring parthenogenesis in some animal species. The whole point of the story is that the event would be impossible except for divine intervention. If anything, animal parthenogenesis counts as (extremely weak) evidence against Christianity, since it makes it possible (though highly unlikely) that the Virgin Birth could have occurred without God existing. (Obviously the hypothesis that Mary lied is a lot more plausible for the naturalist, though...)
The entire book is a conjunction of claims which would be unlikely if Naturalism is true! That is why the book counts as posterior evidence for Christianity. Now I admit that the claims are also somewhat unlikely a priori, but you can't estimate that by asking how frequently they would occur if Naturalism is true.
Just a quick note from my phone. I don't believe I'm assuming naturalism. One in a billion people coming back to life doesn't sound naturalistic to me. I do think I'm assuming induction, but hopefully you'll grant me that. Computing the odds of Christianity given naturalism doesn't make much sense... It's not my fault induction looks a lot like naturalism! Ok, more later, maybe.
It was the comments about the additional improbability of the Virgin Birth which seemed to me to be assuming Naturalism. Is your point that P(random person being resurrected | Christianity) is also quite low? (That is, prior to the General Resurrection of all humans who have ever lived.) That's quite true, but Jesus is not a randomly selected person for a variety of reasons, certainly not from the perspective of Christianity.
(There are some potentially valid concerns, related to the prosecutor's fallacy, if I claimed that Jesus was the Messiah solely because a 1-in-a-billion event (given Naturalism) happened to him, since 1-in-a-billion events happen randomly 1 out of every billion times. But as my post on Bayes' Theorem explains, these concerns can be rebuffed by finding even a single additional piece of weak circumstantial evidence pointing to Jesus as the Messiah.)
I think we're talking past each other a bit. Let me try a slightly different approach. First, let me note that I'm not sure what your view of the bible is, but to me it's not magic, and the various claims it makes have some chance of being right or wrong independently. (I would feel this way even if still a christian.)
Think of the bible as being the address of christianity in the space of all possible religions. It says, take a right at resurrection, a left at virgin birth, another left at the cursed fig tree, etc. For each feature the bible adds, there's some other hypothetically possible religion that makes a different choice. With each additional feature, the space of possible religions that christianity is selected from grows larger. With N binary features you can describe 2^N religions. A priori, if I know nothing, it seems reasonable that all of them have an even chance of being true (actually, some of them may be incoherent, but let's keep things simple).
So my first point was sort of that there's some sense in which having a unicorn and a dragon in your story makes the story strictly less probably than a story in which there's only a unicorn, merely because it's more specific. (Of course, the story might have additional evidence that makes up for this specificity, but that's beyond the scope of priors.)
My second point was that it's not an even split for every feature; given that we've observed lots of people staying dead, stories which have someone not staying dead probably shouldn't start off with a 50% prior. Your point is that if christianity is true, you get all the miraculous things at very little cost, and that I agree with. But it's not quite responding to what I was getting at; before we can talk about whether christianity is true, first I have to be convinced that the story is historical. I mean, you want to use the story as evidence for christianity, right? You can't also use christianity as evidence for the story at the same time... P(bible|christianity) is very high, but that's not an interesting thing to calculate!
Hopefully this is clearer. I think I mixed these two concepts up a little bit previously. Risks of posting late at night...
I'm pretty sure that the point Aron is making here is that you can't separately add in the values of improbable events that are related. To go back to an earlier example, it's very improbable that a person you meet has climbed Mount Everest, and it's very unlikely that a person you meet has climbed K9, but surely you don't find the probability of someone doing both of those things by considering their probability separately. It seems like the class of people who has climbed Everest is more likely to contain the class of people who has climbed other high mountains. In the same way, surely it would be more odd for someone who is otherwise ordinary to have come back from the dead than for someone who had other miraculous features (like a virgin birth and healing people) to do so?
If you really have to consider all the possible religions including the ones that are just the same as Christianity except that Jesus didn't curse a fig tree, then I think that you would end up making everything so improbable that you couldn't believe it. Surely this would apply to other books and historical events too. If you take say, the life of Caesar as told in the history book you happen to have on the shelf and compare it with all other possible lives of Caesar, you would come up with a very low probability of it being true too. Isn't everyone's life stupidly improbable by this reasoning?
lavalamp, I agree that every specific claim of Christianity makes its prior probability smaller. What I'm arguing is that to the extent that the implausibility comes from specificity (as opposed to implausiblity of the specific claims), this large factor is going to be exactly cancelled out by the fact that the testimony of the set of miracles is equally specific.
Yes, that testimony is a posteriori, so you're quite right that it doesn't affect the prior probabilities. But I think it's worth emphasizing this cancellation, because at the end of the day we're only interested in the final result: namely the posterior probability of Christianity. Whatever large numbers may play into that, they don't come from the specificity issue.
Also, I find it a lot easier to intuitively assess the probability values after making the specificity cancellation, since that way it doesn't matter as much how specifically you define the meaning of "Christianity" (e.g. does it include the claim that Jesus appeared to St. Thomas? If so, P(Christianity) gets smaller but P(Thomas appearence | Christianity) increases in a compensating way), and we don't have to divide really huge cancelling numbers with each other. You don't have to do it this way, but it just seems to make the calculations so much easier.
On the other hand, any large numbers entering from the implausibility of the claims themselves would propagate into the final result. This must be compared with the evidential weight of the testimony for the claims. Here my main point is that it should take a lot more evidence to persuade you of your first miracle, than of additional miracles after the first. (Once even one miracle has been established, then we know miracles sometimes happen, so they're no longer weird.)
We seem to agree now on this point, but I think there's still a bit of confusion in your statement that you first need to be convinced of Christianity, before you can benefit from the fact that it implies multiple miracles. The point is that P(lots of miracles | Christianity) isn't really any worse than P(a few miracles | Christianity). So you can't say that the historical documents are particularly implausible because they contain many miracle claims (other than the specificity thing addressed above).
You seem to be invoking some sort of rule against circular reasoning when you say that:
But in the Bayesian analysis there's only two steps: first we consider the prior probabilities, and then we conditionalize on what we know. There doesn't have to be any "before" or "after" in the second step, we can do everything simultaneously. So your suspicion of circular reasoning is misplaced. What I'm really using is the fact that the component parts of Christianity are not all independent, that conditional on certain parts (e.g. Jesus did miracle A) other parts (e.g. Jesus did miracle B) become more probable. Consequently P(Jesus did miracles A & B) is much higher than P(Jesus did miracle A)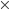
P(Jesus did miracle B).
Do you need me to write the math out more explicitly than this, in an example?
I agree that each additional miracle claim after the first one makes christianity only a little less likely. I should have specified that. I understand the difference between dependent and independent events. I must be being very unclear because you haven't addressed my point.
If everything written in the bible is true, then christianity starts to look like it might be a good explanation precisely because it means the events are not independent and it beats out most if not all theories that have to pay for each miracle separately.
But that's a big "if"! And even if christianity is true, parts of the bible could be corrupted, incomplete, misleading, or fabricated. For this, each bit of the text has to be considered independently. That 1 John 5:7 was probably a later addition is an independent question from whether or not the last few verses of Mark were tacked on.
It's this possibility of the text being wrong that I'm talking about. The bible is not an indivisible unit of evidence which is either 100% correct or 0% correct. And here you do have to pay for each miracle separately, because--whether or not christianity is true--it's always going to seem likely that the miracle is an addition/exaggeration than factual. Miracles are just not that common, even given christianity.
Perhaps I should state my point like this. P(bible|christianity) is high and is relevant to the calculation. But P(bible|~christianity) is also high, so it's not good bayesian evidence.
Can you expand on this? I'm not sure I agree.
Well, if Christianity is true, then the Bible is divinely inspired by God, which might have certain implications for its character. But I don't want to argue for inspiration right now, since I think this is best done after one accepts the main claims of the Bible about Jesus. Instead I'd like to examine the question as if the New Testament were just an ordinary historical document containing testimony, and use that to argue for the core Christian claims about Jesus.
You're certainly right that it's possible for a text to contain both true and false claims. One can consider naturalistic explanations of this sort. However, the factual accuracy of different pieces of the same book of the New Testament are not probabilistically independent. If one piece is factual reporting based on accurate sources, then other pieces are comparatively more likely to be.
It's also true that there are parts of the New Testament documents which are almost certainly interpolations. Fortunately we can tell which parts those are, using textual criticism! I plan to write a post about that.
I don't agree that miracles are uncommon given Christianity, if we're talking specifically about the life of Christ during his earthly ministry. In the Gospels, they seem to be almost as common as dirt. For your argument to work, you'd need to show that if Christianity were true, the Messiah should be expected to perform significantly fewer miracles than are recorded in the New Testament. I see no reason to assume this.
I think that P(Bible|~Christianity) is quite low, for reasons that I'll explain.
Since I'm not discussing here the inherent implausibility of miracle claims, I may as well use a mundane event as an example. Let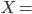
"At 3:28 pm yesterday, Farmer Jones' sow gave birth to seven live piglets, which were subsequently named Blackie, Spot, Pixar, Radish, Vader, Princess, and Racer by his children."
There's nothing particularly implausible or unbelievable about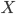
, but nevertheless its prior probability is extremely low due to the large information content. Even if we already knew that Farmer Jones had an sow expecting to give birth, the prior probability of this exact chain of events is lower than 
(
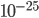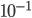for number of live piglets, 
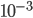per name, and 
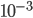for the time of day).
Now consider the conditional probability
. To figure this out we need to know that 
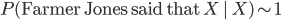(i.e. is within an order of magnitude or so of unity) and also that 
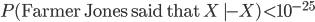. This last comes from the fact that even if Jones' lies or makes a mistake, there's no particular reason for him to say 
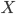, instead of any of the other 
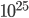things he could have said that are similar to 
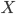, but with different details.
You plug this into Bayes' Theorem, and the big factors of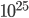
cancel. What we're left with is balancing any implausibility in claim 
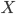with the implausibility of Jones lying. Unless we have some particular reason to be suspicious of Jones or 
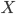, in this case we'd conclude he was telling the truth (or close to it).
g wrote:
Testimony can indeed end up working that way. On the other hand, if you have two or more independent sources for the same extremely specific claim, then you get the large confirmation multiple times, which leads to an extremely high probability for the claim to be true. That assumes strict independence, though. In general, one has to consider the possibility of collusion.
Another way the probability analysis could be more robust, is if there are special reasons to believe that the testimony is particularly reliable, or in other words if the alternatives to them telling the truth are implausible given the circumstances of the case.
Aron, the cancellation you describe is (more or less) exact only in so far as "the source of testimony is basically right about everything" is a live possibility. (Where "everything" means "whatever amount of rightness we're actually considering".)
In the particular case of Christianity, I think this is not the case. The Bible and the broader Christian tradition have repeatedly been found wrong about things. Of course, in such cases Christians decide -- once denial ceases to be an option -- that those things were never really central, but this almost always seems to happen only once there's no real alternative. Examples: geocentrism; life on earth being only a modest number of thousands of years old; humans having been created separately from, e.g., (other) apes; Moses' having written the Pentateuch; books in the Bible with named authors consistently having been written by those authors.
The obvious conclusion is that whatever the Bible is, it isn't close to having been dictated by God; it contains a lot of untruths, including some that were thought important before they were known to be untruths.
Therefore, in particular, its testimony isn't of the sort that gives substantial probability to the whole complicated thing it describes being correct. You may, of course, still say that there's good evidence that it's right about some things, or right about the most important things, or whatever; but we can't rightly say that there's a good chance it's right about everything.
So now what does this mean for the probability that Christians are largely right, despite the complexity of their claims? Well, let's go back to your example of the pig farmer. Suppose you say that Farmer Jones's pig gave birth to piglets with particular names, and suppose it turns out that you say this only because you read a report to that effect in the Pig Fanciers' Gazette. And suppose it further turns out that the PFG didn't have a reporter on the scene, or interview Jones directly, or anything like that. Then I submit that the more piglets' names you have in your list, the more likely you are to be substantially wrong (whether that means "any mistakes at all" or "less than 90% right" or "less than 50% right" or whatever). In other words, this is not a situation where the improbabilities simply cancel out.
Oh, by the way, a very merry Christmas to one and all. Or, for those who prefer, a very merry Newtonmas.
g is phrasing my argument better than I was, so just a quick technical comment:
This doesn't make any sense. In a Bayesian framework (and probably all others), unity is infinitely far away, nothing can be a "few orders of magnitude away" from it. To see this, convert to log odds-- unity is literally at positive infinity and 0 is at negative infinity. Or consider that if you start at unity, no amount of evidence will cause you to update away from unity.
And on a separate point, I deny that farmer Jones's error rate is anywhere near zero! I'd bet he can't say a thousand correct things in a row, for example.
Anyways, merry Newton/Christmas .
lavalamp,
binary operator, defined over pairs of positive real numbers. According to this definition, a probability satisfies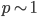 
unless 
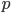is very small.
Regarding my symbolic notation, it's just a definitional convention. I was using the usual
You're quite right that there's a sense in which
is infinitely far away in Bayesian epistemology, and that you can define an alternative sense of the vauge comparison symbols 
(much greater than), 
(much less than), and 
(roughly the same size) using log odds. But nothing forces me to adopt this alternative convention if I don't want to, and I didn't. If I had written my formulae in your language, I would have said it's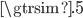 
.
UPDATE: It looks like my LaTeX plugin doesn't have \gtrsim installed. It looks like a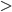
on top of a 
and means "greater than or of approximately the same order as". The absence of this symbol is another reason for me not to use lavalamp's convention.
Support for \gtrsim and other AMSmath symbols is actually available. The easiest way to enable it is like this:
On your Dashboard, go to Settings->Latex.
On the configuration page this gets you to, you scroll down to the "MathJax Server" section and select the "Custom Service" radiobutton. In the line beside that button you paste in the address from the default option above (what you are now using), except replacing "default" with "TeX-AMS-MML_HTMLorMML". Then press "Update Latex Options" and the AMS symbols become magically available.
(Sorry, I don't have anything to add on the actual discussion, because to frequentist me it looks like you're clearly right about everything except the root error of Bayesianism itself.)
I think you're changing the subject here, since my Bayesian calculation was intended to argue for some specific core doctrines of Christianity (God, Jesus, the Resurrection etc.) rather than to argue for anything like a doctrine of biblical inerrancy. I'm dealing with a subset of the Bible (the most important claims of the historical parts of the New Testament) and, if you like, a subset of what "Christianity" might be taken to mean. So I don't think this criticism is really on target to what I'm saying. But I'll respond briefly to it anyway.
Regarding your scientific examples, its just not true that all Christians believed they were equally central to the faith as the Resurrection. Neither St. Augustine nor St. Aquinas thought that Genesis needed to be taken as a literal scientific account, for example, and I get the sense from reading St. Athanasius' On the Incarnation that he wouldn't have been bothered at all by human beings being descended from animals, since he spends a lot of time talking about how we are mortal animals by our nature. Since these are arguably the 3 most influential theologians for Western Christianity, after the apostles and before the Modern Era, I don't think these examples are cherry-picked.
Regarding your biblical criticism examples, I actually do believe that every book of the New Testament which names its author was probably written by that author, and I don't think the arguments against authorship are particularly convincing. I don't accept the JEPD documentary hypothesis, which I think has way too many free parameters compared to its explanatory power. Nor do I think it at all likely given Jewish culture that the Torah was first compiled during the Exile (and then forced on the Samaritans who had been politically disunited with the Jews since around 930 BC?). In fact, I don't think the biblical critics know any hard facts that are inconsistent with this modified-traditionalist hypothesis: A) The sources that went into the Torah were assembled under the direction of Moses, B) it was assembled into something close to its current 5 book form by the end of the lifetime of Joshua, and C) during the period of the monarchy, the priests felt free to engage in light editorial updating, of which there are clear signs. (Remember they hadn't invented footnotes yet, so comments which we would make as footnotes got incorporated into the text.)
I don't consider these hypotheses to be essential to my faith either, because Jesus is the thing which is essential to my faith. The authorship of the New Testament documents is of course indirectly very important, since I need at least some (though not necessarily all) of the historical documents to be reliable (but not necessarily 100% accurate regarding minor details) to get to the Resurrection.
Regarding the piglets, I wish that it were possible to make simplified models to illustrate basic points about probability theory, without people assuming I must be ignorant of any other basic points I happen not to mention in that example. If the only two hypotheses on the table are that Farmer Jones is inerrant, or else that Farmer Jones is a pathological liar, then the probabilities work the way I said. If we (more reasonably) consider as our "truthful" hypothesis that Farmer Jones is trying to be honest but only remembers piglet names correctly 98% of the time (say), then of course "Farmer Jones says X" is good evidence, not for X, but for "X is approximately 98% true or better". That is, if X is sufficiently long.
Huh? The probability of getting things 100% right does decrease with the number of names, but the probability of getting above 90% or 50% should converge to some finite number (the probability that the reliability of PFG's gossip chain is at least this reliable, when it comes to passing on the names of piglets). Or is your hypothetical supposed to implicitly include an assertion that the PFG is known for sure to be less reliable than this?
I also wish a blessed and merry Newtonmas to anyone who wishes to celebrate it. Even if he was rather unscrupulous from an ethical perspective. Better than Christopher Columbus though, who was rotten both scientifically and ethically.
Thanks very much, Gilbert. It seems to work now.
If you believe everything but the Bayesianism, then maybe I need a post arguing for that. Are you familiar with the Dutch Book Argument? And out of curiosity, how would you as a frequentist examine the evidence for and against a claimed unique historical event (something which, if it happened at all, only happened once)? And if the claim seemed intuitively implausible, how would that factor into the analysis?
Do frequentist methods really fail dutch book scenarios? I hadn't thought it was that bad. This paper (explaining how to combine p-values) is (accidentally) the best argument for Bayesianism I've seen. :)
This has gotten a bit unfocused, so let me try to map our actual points of disagreement.
1. P(bible|~christianity) I think it's highish, you think it's low. I won't argue for this here, it's off topic in this already long thread.
2. I generally agree with the more liberal biblical textual criticism folks. JEPD seems to have enough support to be plausible. I think laterish dates for many of the new testament books are more likely to be correct, except for Paul's books (the ones actually written by him), which probably were written at the commonly thought dates. I think even if the most conservative dates for the gospels are correct, it's bad news, as it still means a lot of time passed with them being an oral tradition. I think the late canonization and the prevalence of extra-canonical gospels implies that the bible has a significant element of "history is written by the victors". The evidence for Q seems reasonable for me. Etc. I won't argue for these things here, as again it's off topic for this post.
3. Finally, on topic... Say someone presents you with a hypothesis with N binary elements. We both seem to agree that there's a complexity penalty on the order of 2^N. However, if I'm understanding you correctly, you seem to think that the mere fact that this person presented you with this particular hypothesis pays for most or all of this complexity. I went back and read your explanatory post again now that I understand your notation. I'll think about it a bit more and try to make another comment in response.
Aron, I don't think I was changing the subject and I wasn't claiming that you were arguing for biblical inerrancy. My point is that "testimony makes the big factors cancel out exactly" only applies in cases where the testimony has a good chance of being basically all correct.
I didn't say (and didn't mean) that all Christians (or most Christians, or any Christians) believed that things like a relatively recent creation were as central to the faith as the Resurrection. (That would be ridiculous. To many versions of Christianity, the Resurrection is the most central doctrine; to most others it's at least very important indeed.) I said only that until they were refuted, those doctrines were regarded by many Christians as important parts of the faith. Your specific examples seem to me to miss the point; I didn't say anything about taking Genesis as a literal scientific account, and saying that we are mortal animals by our nature is a very different matter from saying that we are descended from other mere mortal animals. I don't think Athanasius would have objected to common descent on the grounds that we aren't animals; I think he would have objected to it on some or all of these grounds: that Genesis says something very different (note: being bothered by this doesn't mean treating it as a science textbook); that Paul's (anti)parallels between Adam and Christ make little sense if there wasn't a real Adam; that the church had always held that human beings were created (as human beings) by God; that it is impossible for a creature with a rational mind and a soul to be born of one with neither. (I will remark irrelevantly that CSL' s preface to that translation of the De Incarnatione is very good.)
Of course the question isn't whether there are "hard facts that are inconsistent" with your proposed almost-traditional hypothesis, but whether the hard facts (and, so far as there are such things, the soft facts) make it less probable than less-traditional hypotheses. I am concerned that you may be doing two things that are separately quite reasonably but jointly unsound: justifying a traditional position on the authorship of the biblical texts on the basis of accepting (a particular version of) the Christian tradition, and justifying your acceptance of that version of the Christian tradition on the basis of an analysis of those texts that depends on the traditional ascriptions. But we'll see in due course :-).
For the avoidance of doubt, I don't think I was assuming you to be ignorant about anything, and if I seemed to be then I apologize (1) for inept writing and (2) for any resulting annoyance or hurt. On the piglets, we are agreed: if the "truthful" hypothesis is that Jones is right a fraction p of the time, then his saying something is evidence only for its being approximately p-right, so to speak. And yes, my hypothesis about the Pig Fanciers' Gazette (and the Bible) is that for them there is good reason to think that p is rather small.
Newtonmas is, of course, a celebration not of Newton's character but of his discoveries.
I was thinking more about the results that anyone who isn't Dutch bookable must be capable of being represented as a Bayesian reasoner. So that any time a frequentist doesn't get themselves into trouble, you can think of them as being crypto-Bayesian, but with a set of prior probabilities which may not be very sensible.
Have you considered just how big of a complexity penalty the hypothesis should get, when you consider that it starts by (more or less arbitrarily) assigning chapters or verses to J, E, or P? (And then claiming there are identifiable similarities in each source.) Is this complexity less than its explanatory power?
Have you considered the fact that the documentary hypothesis was first invented at a time when people were trying to find hidden sources all over Homer, Beowulf, Shakespeare, etc. and that the general methodology has since been abandoned by nearly every other field of textual criticism, besides biblical studies?
The New Testament biblical criticism should probably go in its own post. I didn't want to suggest I disagree with everything in biblical criticism. I accept that Mark was the first gospel to be written, and that Q is a plausible (but not proven) hypothesis for explaining the remaining similarities of Matthew and Luke. But I think a lot of the more aggressive claims of secular biblical critics are based on huge doses of circular reasoning.
But I will note here that serious scholars, including secular ones, nearly all date the Gnostic gospels to the 2nd-4th centuries, and all or nearly all books of the New Testament to the 1st century. (The one exception is the Gospel of Thomas which some think is 1st century, although more say 2nd.) Also, the New Testament books were widely read and quoted long before any official canonization decisions. They also portray Jesus as much more Jewish than the gnostic gospels do. I don't think that narrowing down the sources to 1st century documents counts as "history is written by the victors".
Yes, so long as it's possible that the person has access to the truth of the matter. If they made it up for no reason, that would be different. It would also be different if the person had reason to make up that specific falsehood. If Farmer Jones claims X in response to a randomly generated query "Do you have piglets with the following 7 names: [as in X]?" then his claim is not even remotely plausible.
Continuing the off topic discussion....
Yeah, there's definitely a complexity penalty there. I had thought there were actual like word choice statistics behind the assignments, because otherwise how could anyone believe such a thing? But it looks like there aren't, so my P(JEDP is essentially correct as stated) just dropped below 20%. It should be possible to write a computer program to statistically test the assignments. I don't care enough to go out and do this though. It still seems probable to me that there were multiple authors. I am reminded of how terrible the entire biblical studies field seems to be.
I think I figured out what's bothering me about your Farmer Jones example.
I don't agree that P(Farmer Jones said that X|~X) < 10^−25. Specifically, I don't agree that all of the possible corruptions of the facts are equally likely.
If I start with a prior of 10^-25, and give him two orders of magnitude for each assertion (assuming that he is 100x as likely to say a true thing as a false thing), I end up with a remaining probability of something like 10^-7. This suggests that the statement is probably not 100% accurate. However, it's almost certainly highly correlated with the truth. I expect that small mistakes are vastly more likely than large mistakes. So, I expect it's most likely that he got the time or one of the names slightly wrong.
If one of his kids is with him, I expect the kid to pipe up with something like, "No, dad-- it's Spotty, not Spot!" And then I'll likely believe everything else, too, because I'll give it 1.5 orders of magnitude (kids are less reliable than adults) from the kid's implicit agreement, which will be enough to push the probability up to about 10^4 (er, I mean something like (10^4 - 1)/10^4, log odds are so much better to work with).
Except the time. That's obviously not correct, you can't have seven piglets in one minute. ;)
(Actually, since his statement doesn't nail down what the time is referring to (beginning or end of birth process), we shouldn't ding him 10^-3 for the time, IMO; it's not really accurate to the minute.)
It can't be right that the probability of correctly remembering 7 names by yourself is 1 in 10 million. That's equivalent to saying that Jones has only a 10% chance of remembering each name. So your probability analysis is still whacked out.
At the risk of sounding like a teacher assigning homework, let me suggest that you do a full Bayesian analysis of the situation, dotting every i and crossing every t, using only the following 2 "theories" of the situation: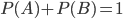
repectively. (1) What are the odds that farmer Jones gets all 
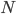names right, and (2) in the limit that 
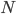is large, what is the approximate fraction of the names that he gets right? In the case where 
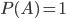, ignoring the difference between 100 and 101, You should get something like
A) Farmer Jones is truthful and gets names right:wrong in a ratio of 100:1, or
B) Farmer Jones is a liar and makes up names randomly.
which can be assigned prior probabilities of
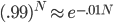
for the first question (which is about .93 for(If you'd like a harder problem, you could assume that Farmer Jones' reliability is a continuous, but not necessarily uniform, probability distribution).
Oops! And here I thought I was being so careful, looking up what was a plausible number of live piglets for a sow to have at once...
To stave off a possible misunderstanding, I'm a Christian. By calling Bayesianism a "root error" I don't mean it's at the root of your thus escapable faith, I mean the conversation that grows from it is basically moot.
On to statistical ideology:
In a system where credence is always a real number, and all propositions and conditional propositions have credences attached to them, and there is a stream of confirmations and disconfirmations of propositions, so that the credences need to be updated, I actually agree that that updating needs to happen according to The Rev. T. Bayes's theorem. (Or something equivalent, if we're talking odds ratios or logarithms or whatever, then the formal rule will be different, but there will always be some isomorphism to the canonical one.) Basically I'm aware of Cox's theorem and where its preconditions hold I'll except its consequence.
But I think that's a rather big set of assumptions if you want to talk about all beliefs. Basically, when people talk about probabilities I want to know what model they are talking about. On what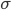
-algebra does the probability measure live, what structures does that presuppose in reality, how do those numbers relate to experience, etc. Frequencies of repeatable events are the paradigmatic way of answering that question, but I'd agree that some other ways are possible.
For example, consistent betting odds on all relevant events are one way to do it. But look at the baggage that introduces: First, it assumes a structure of possible events. For example, if you bet on who will win an election, there will be a (probably implicit) understanding that the bet is off if there is a revolution and the election gets canceled, because that just doesn't count as an 'event' in the probability space you're considering. Likewise, any bet for money is moot if money gets abolished in some kind of communist revolution. Second, it assumes that bets will be decisively settled by future information. That makes it basically impossible to bet on controversial past events, where new information is unlikely to be forthcoming. Third, it assumes that people have beliefs on all relevant events and are willing to bet on them for profits of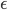
. But real people are ignorant and risk-averse and rightly weary of asymmetrical information. Now often this is close enough for practical purposes, which is why insurances and bookmakers can stay in business. But it is still a model and the probability-talk is only meaningful in that model.
And I can make similarly restricted models of rationality that don't involve beliefs being real numbers. For example, one could imagine binary beliefs with ordinal certainties. In that model beliefs would change iff they turn out incompatible with beliefs of higher precedence. The path-dependance could be removed by alway evaluating all evidence against the original belief set. Intuitive (im-)plausibility would be encoded in the preference order. And yet the model doesn't include any real numbers. There is no question of how certain one is of a given belief, only of which of two beliefs one is more certain. Of course this is a cartoon of the actual thinking process, but then so is Bayesianism.
As for what we actually do, I think the process is basically evidence and rational minimum standards constraining possible beliefs and gut feelings within that constraints. And I think most of the debate on this post could be translated to that process without loss of persuasiveness. Some probabilities get canceled out without being named and others are given as large ranges. Nobody ends up with an actual numerical probability for Christianity. And the question whether two factors cancel out could easily be replaced with the question whether some scenarios are plausible. To me that looks a bit like the Drake equation, where a wild guess suddenly sounds a lot more sciency, but looking closer it's just replaced with six wild guesses. Of course you have a good argument rather than a wild guess of a number, but I think the problem of the indeterminate formalization not really adding anything is the same.
Gilbert,
I'm moving this conversation to the Bayes' Theorem thread, since that's where it belongs. My reply to you is there.
This has been bugging me for a while now. The below isn't what you're asking for, because I'm not sure you're asking for the right thing. :)
First, I'm going to assume some excellent semantic compression algorithm exists, so that I can treat all hypotheses as bit strings. I'll assume that this algorithm works such that a one bit change in the bit string will make a small change in the english version of the hypothesis (e.g., "dog" -> "doggy" or "6" -> "7" or "happy" -> "not happy").
OK, so with that in mind, it's clear that with N bits, you can describe 2^N hypotheses. The chance of a random number generator giving you any of them is obviously 2^-N.
OK, but the question we're trying to answer here is, "how much evidence for a given hypothesis does a statement by a human provide?" So there's some chain of events that causes the human to verbalize a hypothesis. It at least includes that human's observations, interpretations, memories, and reports. A complete model also needs to include factors like whether the human is crazy, purposely lying, trying to sell us something, exaggerating, etc. We're going to assume for this example that those aren't factors. To make it easy, I'll lump all the various sources of error together and assume that along the path from observation to giving a report, there's a 1/100 chance that a bit will get changed.
So with that assumption, reports from a human follow a binomial distribution. 100 bit hypotheses will have a 1 bit error on average.
If we give FJ's story a complexity penalty of 10^-25, that implies it should be about 83 bits if compressed by my semantic compressor, and therefore it's most likely that FJ made no errors at all. The chance that he made a one bit error is .43, if I plugged the numbers in right. This seems to match my intuition that there's a substantial but not overwhelming chance that he got one of the names or the time just a little bit wrong. (And is significantly different than my previous suggestion.)
So for longer hypotheses, this implies that number of errors scales linearly with N, not exponentially. So, perhaps a decent approximation is to charge a complexity penalty of one bit for every 100 bits of length. Converting .01 * 83 = .83 bits to dB, I get something like -.25dB for the FJ story (or you could just take .01 * 25 directly). I'll admit that this seems a lot more reasonable than -70dB. This model conforms to my intuition that long stories almost certainly have errors.
To really do the math correctly, I think you'd need to do the bayesian updating with the entire probability mass function; but that'd be a lot more cumbersome than converting to dB and adding, and in fact I'm not entirely sure how to do that off the top of my head.