One of the things I've been trying to do on this blog is to explain Einstein's theories of relativity. Here are my previous posts on this subject:
Time as the Fourth Dimension?
The Ten Symmetries of Spacetime
Fields
Geometry is a Field
Coordinates don't matter
All points look the same
The first two have to do with Einstein's first theory of Special Relativity, in which spacetime is taken to be fixed. The third post describes what fields are. The last four describe his second theory, General Relativity, in which the geometry of spacetime is itself a field: the gravitational field.
The gravitational field is also called the metric 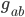 , where
, where 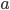 and
and 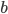 are indices selected from the four spacetime dimensions
are indices selected from the four spacetime dimensions 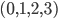 . However, the exact form of the metric depends on your choice of coordinates, and it is always possible to pick coordinates so that the metric at any point looks just like the metric of Special Relativity. For this reason, in order to discuss curved spacetimes (those that differ from the flat spacetime of Special Relativity, e.g. the gravitational field of the Sun or the Earth) we need to compare the metric at different points.
. However, the exact form of the metric depends on your choice of coordinates, and it is always possible to pick coordinates so that the metric at any point looks just like the metric of Special Relativity. For this reason, in order to discuss curved spacetimes (those that differ from the flat spacetime of Special Relativity, e.g. the gravitational field of the Sun or the Earth) we need to compare the metric at different points.
The basic idea is this: Suppose we are sitting at one particular point 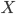 of spacetime, and we imagine we have an infinitesimal arrow whose base sits at the point
of spacetime, and we imagine we have an infinitesimal arrow whose base sits at the point 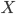 and which points (ever so infinitesimally) away from
and which points (ever so infinitesimally) away from 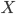 in some direction. We call such a thing a vector and write it as
in some direction. We call such a thing a vector and write it as 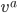 , where
, where 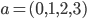 . This is actually a set of four numbers:
. This is actually a set of four numbers: 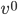 would be a number saying how far
would be a number saying how far 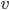 points in the 0-direction,
points in the 0-direction, 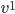 would be a number saying how far
would be a number saying how far 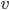 points in the 1-direction, and so on.
points in the 1-direction, and so on.
Now, suppose we take this vector on a vecation tour through spacetime. Perhaps it would be simpler just to think about space for a minute. Imagine vectors lying on a 2-dimensional sphere. (Warning: when an ordinary person uses the word sphere, they usually mean to include the interior, but when a math or physics person says sphere, they only mean the surface!) Imagine for example, that the vector 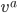 lies on the surface of a Earth, and pretend that the vertical up-down direction doesn't exist. So on a random point on the Earth's surface,
lies on the surface of a Earth, and pretend that the vertical up-down direction doesn't exist. So on a random point on the Earth's surface, 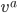 can point north, south, east, west, or in-between, but it can't tilt up or down.
can point north, south, east, west, or in-between, but it can't tilt up or down.
Imagine that 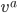 starts on the North Pole, pointing towards Hawaii. Suppose we slide the vector down in the direction it is pointing, until it hits the Equator. The vector now points South. Now let's drag the vector 1/4 of the way around the Equator, without rotating it. The vector still points South. Finally we drag it back to the North Pole. It has now been rotated 90 degrees from its original position! This is true even though on each step of the journey, we were careful not to rotate it as it travelled. (Dragging vectors without rotating them is called parallel transport, by the way.)
starts on the North Pole, pointing towards Hawaii. Suppose we slide the vector down in the direction it is pointing, until it hits the Equator. The vector now points South. Now let's drag the vector 1/4 of the way around the Equator, without rotating it. The vector still points South. Finally we drag it back to the North Pole. It has now been rotated 90 degrees from its original position! This is true even though on each step of the journey, we were careful not to rotate it as it travelled. (Dragging vectors without rotating them is called parallel transport, by the way.)
This happens because the geometry of the surface of the Earth is intrinsically curved, i.e. the geometry of the sphere is not flat. This must be distinguished from extrinsic curvature, which refers to something of lower dimension being bent within a higher-dimensional space. The surface of the Earth is extrinsically curved in our ordinary 3-dimensional space, but that's not what were talking about. We're talking here about the geometry of the sphere, quite apart from whether it is or is not embedded in some higher dimensional space.
The distinction is quite important in the case of our 4-dimensional spacetime, because (as far as we know) it is not embedded in any kind of higher-dimensional space. When we say that spacetime is curved, we do not mean that spacetime is sitting in some kind of "hyperspace" in which it is bent into a funny shape. We mean that if you move vectors around in spacetime in a loop (i.e. a path that starts and ends at the same spacetime point 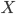 ), it may come back rotated compared to its original position. That is what curvature means.
), it may come back rotated compared to its original position. That is what curvature means.
I should note that it's okay to drag these vectors either forwards or backwards in time, or along spacelike directions. That's because these are imaginary vectors serving as a visualization aid to probe the geometry of the spacetime. They aren't tangible physical objects which have to travel slower than light, and towards the future.
Now, ever since Archimedes, math people have liked to study things by breaking them up into tiny infinitesimal pieces. So we want to think about what happens if you drag a vector around an infinitesimal loop. To define this, we imagine we have a vector 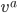 , which we drag around in a tiny parallelogram whose sides are given by vectors
, which we drag around in a tiny parallelogram whose sides are given by vectors 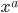 and
and 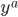 pointing away from
pointing away from 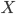 . When we drag
. When we drag 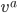 along this parallelogram, if there is curvature it can come back rotated as an ever-so-slightly different vector
along this parallelogram, if there is curvature it can come back rotated as an ever-so-slightly different vector 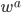 . To keep track of this we write:
. To keep track of this we write:
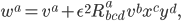
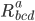 is a gadget with four indices known as the ``Riemann curvature tensor'', which keeps track of the amount of curvature at any given point
is a gadget with four indices known as the ``Riemann curvature tensor'', which keeps track of the amount of curvature at any given point 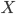 .
. 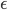 is an infinitesimally tiny parameter which keeps track of how big the sides of the unit parallelogram are, for vectors of some unit length.
is an infinitesimally tiny parameter which keeps track of how big the sides of the unit parallelogram are, for vectors of some unit length.
What's a tensor? The metric 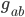 , vectors such as
, vectors such as 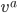 , and
, and 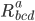 are all examples of tensors. Tensors are similar to vectors, except that they are allowed to point in any number of directions. A tensor is a kind of field which is allowed to depend on two things: 1) which point you are at in space and time, and 2) zero or more spacetime indices written as subscripts or superscripts
are all examples of tensors. Tensors are similar to vectors, except that they are allowed to point in any number of directions. A tensor is a kind of field which is allowed to depend on two things: 1) which point you are at in space and time, and 2) zero or more spacetime indices written as subscripts or superscripts 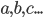 . These indicate the total number of vectors it takes as inputs or outputs. Note that the Riemann curvature has 3 of its indices downstairs and 1 upstairs. That notation tells us that it eats 3 vectors as inputs and spits out 1 vector as an output.
. These indicate the total number of vectors it takes as inputs or outputs. Note that the Riemann curvature has 3 of its indices downstairs and 1 upstairs. That notation tells us that it eats 3 vectors as inputs and spits out 1 vector as an output.
In any equation involving tensors, each index letter is repeated, either 1) once in each term of the equation, always upstairs or always downstairs, or 2) twice in the same term of the equation, once upstairs and once downstairs. In case (1) we interpret the tensor equation as being true for any possible choice of index, as long as it is the same for all terms, on both sides of the equals sign. In case (2), we consider all 4 possible choices for the index and add them together (the Einstein summation convention). These rules prevent us from doing nonsensical things like e.g. trying to add scalars and vectors together.
Tensors are not themselves coordinate-invariant, but when you change your system of coordinates, the value of the tensors changes in a particularly simple way. This makes them useful when trying to describe physics in a coordinate-invariant way. So long as you follow the rules in the previous paragraph, a tensor equation is a coordinate-invariant idea, i.e. if it is true in one coordinate system it is true in all of them. That's because if you change your coordinates, both the left-hand-side and the right-hand-side of the equation change in the same way, so it doesn't matter.
The last thing I need to say here is that the Riemann curvature tensor 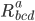 is not a new field additional to the metric tensor
is not a new field additional to the metric tensor 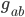 . If you know what the metric is, you can work out the Riemann tensor. At any given point,
. If you know what the metric is, you can work out the Riemann tensor. At any given point, 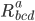 depends on the metric
depends on the metric 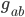 , its first derivative
, its first derivative 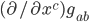 and its second derivative
and its second derivative 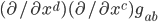 . But the formula looks complicated, so I'll spare you for the time being, until I can think of a simple way to justify it.
. But the formula looks complicated, so I'll spare you for the time being, until I can think of a simple way to justify it.

Nitpick: The derivatives you want at the end are of the metric tensor, not the Riemann curvature tensor.
Yikes! Thanks for catching that. It's fixed now.