So far in my explanation of General Relativity, I've discussed the metric 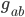 , from which one can calculate the curvature tensor
, from which one can calculate the curvature tensor 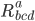 by way of the connection
by way of the connection 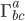 .
.
In practical astrophysical contexts:
- The metric is related to the gravitational potential at a point, i.e. how much ``potential energy'' a unit mass will have sitting in the gravitational field. But I haven't said anything about energy yet, so you're entitled to ignore this remark...
- The connection (which involves a derivative of the metric) tells you the gravitational force at a point, i..e the amount by which freely-falling objects will accelerate in a given coordinate system.
- Finally, the curvature (which involves a derivative of the connection) tells you the tidal forces at a point, i.e. a difference in the force acting on a nearby object. Yes, the ocean tides happen because the moon's gravitational field has nonzero curvature at the Earth's location. That's why it's called that.
So far this is just the kinematics of general relativity—that is, what kind of entities are involved, and the basic outline of their behavior. For example, If I wanted to tell you the kinematics for basic Newtonian mechanics (what you learn in high school physics), I'd say that A) there are a bunch of objects which have masses and positions (and orientations if you want things to get complicated...), B) the position of an object can change with time, but its mass is ``conserved'' and therefore doesn't, and C) if you want to work out the ``force'' of an object, you can do so using 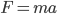 .
.
OK, so I've told you all about Newtonian Mechanics, and now you can go use it to solve problems, right? No, of course not! You can recite "the time-derivative of the position is the velocity, the time-derivative of the velocity is the acceleration, and the acceleration equals the force over the mass" over and over again, but it's totally useless until I tell you what the forces actually are! Without that, you can't make any predictions at all about what the objects are doing.
Unless you count boring predictions like "the object will be somewhere", you need to know something else. This something else is called the dynamics, which means the rules for how things actually change with time. (For example, if I told you that any two objects with mass 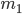 and
and 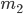 at a distance
at a distance 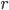 are gravitationally attracted towards each other's positions, with a force that is proportional to
are gravitationally attracted towards each other's positions, with a force that is proportional to 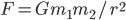 , and if you know the initial positions and velocities, then you can work out their orbits! At least, you can if you're clever at math, like Newton was.)
, and if you know the initial positions and velocities, then you can work out their orbits! At least, you can if you're clever at math, like Newton was.)
So we need to write down an equation which says how things can change with time. We call this the equations of motion. Ever since Newton wrote down 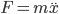 (each dot being a time derivative, so that his archnemesis Leibnitz would have written
(each dot being a time derivative, so that his archnemesis Leibnitz would have written 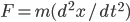 to say the same thing) we've realized that these equations typically involve taking two derivatives. So we shouldn't be surprised that the equation of motion for general relativity involves the curvature tensor
to say the same thing) we've realized that these equations typically involve taking two derivatives. So we shouldn't be surprised that the equation of motion for general relativity involves the curvature tensor 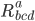 , since it's a double derivative of the metric, which is the basic field of General Relativity.
, since it's a double derivative of the metric, which is the basic field of General Relativity.
To write down the equations of motion, we need to massage the curvature tensor a little bit. If you've forgotten the ground rules for tensors, click on the link. We start with the the Riemann curvature tensor 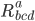 . Since each of the letters is a spacetime vector index with four possible values, it looks like this has
. Since each of the letters is a spacetime vector index with four possible values, it looks like this has 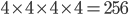 components. Fortunately there are a lot of symmetries and constraints, so there's actually only 20 independent components per spacetime point. We can define the Ricci tensor
components. Fortunately there are a lot of symmetries and constraints, so there's actually only 20 independent components per spacetime point. We can define the Ricci tensor 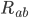 by contracting the top index with the middle index on the bottom, like so:
by contracting the top index with the middle index on the bottom, like so:
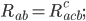
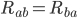 ), it only represents 10 out of the 20 curvature components. If this is not enough simplification for you, we can go further by contracting again using the inverse metric:
), it only represents 10 out of the 20 curvature components. If this is not enough simplification for you, we can go further by contracting again using the inverse metric: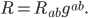
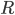 is called the Ricci scalar, because it has just one component.
is called the Ricci scalar, because it has just one component.
Whew! Without further ado, here's the equation of motion for General Relativity, called "the Einstein equation" after you know who:
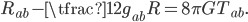
The 8 and the 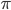 are the same numbers which you learned about in school.
are the same numbers which you learned about in school. 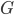 is Newton's constant, which I sneakily introduced earlier in this post. Note that the
is Newton's constant, which I sneakily introduced earlier in this post. Note that the 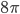 isn't really just there for backwards compatibility with Newton's force law. If Einstein's equation had been discovered first, we would have left out the
isn't really just there for backwards compatibility with Newton's force law. If Einstein's equation had been discovered first, we would have left out the 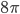 from it, and then we would have written the force law as
from it, and then we would have written the force law as 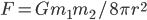 . But as it is, Newton got his
. But as it is, Newton got his 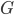 before Einstein did, so we're stuck with it.
before Einstein did, so we're stuck with it.
But the really important symbol here is 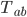 . This is the energy-momentum tensor, or (because why should anything have only one name!) the stress-energy tensor. It's a
. This is the energy-momentum tensor, or (because why should anything have only one name!) the stress-energy tensor. It's a  symmetric matrix which tells you how the energy and momentum of matter (stuff) are flowing through a given point. Now if you are a true Israelite in whom there is no guile, you should be asking: "What on earth (or in the heavens) are energy and momentum! You haven't explained that yet!" No I haven't. For now, let's just say it's a property of matter, but we will get to it in a later post.
symmetric matrix which tells you how the energy and momentum of matter (stuff) are flowing through a given point. Now if you are a true Israelite in whom there is no guile, you should be asking: "What on earth (or in the heavens) are energy and momentum! You haven't explained that yet!" No I haven't. For now, let's just say it's a property of matter, but we will get to it in a later post.
The combination of curvatures 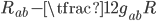 which appears on the left-hand-side is also known as the Einstein tensor. It has the same 10 components as the Ricci tensor
which appears on the left-hand-side is also known as the Einstein tensor. It has the same 10 components as the Ricci tensor 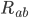 ; they're just repackaged a bit differently. So the Einstein equation is actually 10 equations.
; they're just repackaged a bit differently. So the Einstein equation is actually 10 equations.
So, if you know what the matter is doing, you can figure out something about the geometry of matter. At least, you can figure out the 10 of the components of the curvature which correspond to the Ricci tensor 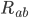 . Since the full Riemann tensor
. Since the full Riemann tensor 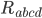 has 20 components, there are 10 components left which are undetermined. The remaining 10 components are called the Weyl tensor, and can be nonzero even in regions in which there is no matter. That's why there can be tidal forces outside of the surface of the sun or moon, even though there isn't any solar or lunar matter there. It's the Weyl tensor which does that. Also, as I wrote in Geometry is a Field:
has 20 components, there are 10 components left which are undetermined. The remaining 10 components are called the Weyl tensor, and can be nonzero even in regions in which there is no matter. That's why there can be tidal forces outside of the surface of the sun or moon, even though there isn't any solar or lunar matter there. It's the Weyl tensor which does that. Also, as I wrote in Geometry is a Field:
There can also be distortions of the spacetime geometry which exist independently of matter. These gravity waves are to gravity what light is to electromagnetism, ripples in the field which travel through empty space, and can be emitted and absorbed. The propagation of these waves is also determined by the Einstein equation. Since gravity comes from massive objects, gravity waves are emitted when extremely large masses oscillate, for example when two neutron stars orbit each other. We know gravity waves are there, but we haven't detected them directly. However, we hope to detect them soon with the LIGO experiment.
It's also the Weyl tensor which allows for gravity waves.
Clever readers may notice that I never wrote down what the Weyl tensor actually is. There's a clever formula where you start with 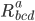 , and then cleverly suck out all of the information about
, and then cleverly suck out all of the information about 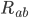 , and end up with the Weyl tensor
, and end up with the Weyl tensor 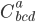 . But it's a bit complicated, so don't ask. The important thing is even when all of the components of
. But it's a bit complicated, so don't ask. The important thing is even when all of the components of 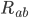 are zero,
are zero, 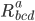 doesn't have to be zero.
doesn't have to be zero.
When we say that the Einstein equation is the ``equation of motion'' for General Relativity, we mean that you can use it to work out how the metric changes with time. So, if you know the metric everywhere at some ``time'' which we will call $t = 0$ (think of this as being like the position of the gravitational field), and if you also know its first derivative 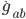 (think of this as being like the velocity), and if you know what the matter is doing, then the Einstein equation (which is like the force law) lets you work out the second derivative
(think of this as being like the velocity), and if you know what the matter is doing, then the Einstein equation (which is like the force law) lets you work out the second derivative 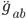 . By continuing to apply the Einstein equation, you can work out the value of the metric for all time!
. By continuing to apply the Einstein equation, you can work out the value of the metric for all time!
Well, not quite. Remember that coordinates don't matter! This means that we can't actually hope to totally determine the metric, since if we start with a metric which obeys the Einstein equation, and distort it by changing the coordinate system, we get an equally good solution to Einstein's equation. So what we should really say, is that if you know the metric and its first derivative at 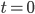 (and you know how matter behaves so you can figure out
(and you know how matter behaves so you can figure out 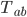 ), then you can determine the fields at
), then you can determine the fields at 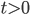 or
or 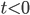 up to coordinate transformations.
up to coordinate transformations.
So we can actually only need to figure out 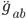 up to coordinate transformations. There are 10 components of
up to coordinate transformations. There are 10 components of 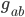 , but there are also 4 spacetime coordinates
, but there are also 4 spacetime coordinates 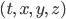 whose values can be freely determined. As a result, we actually only need to use 10 - 4 = 6 of the Einstein equations in order to figure out how the metric changes with time.
whose values can be freely determined. As a result, we actually only need to use 10 - 4 = 6 of the Einstein equations in order to figure out how the metric changes with time.
The remaining 4 equations are called constraints, because they don't involve second derivatives of the metric. Instead, they restrict which values of 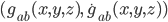 you are allowed to start with. These constraints are one of the most subtle features of General Relativity, because they ensure that the total energy and momentum of an object (like the sun) are encoded in the gravitational field coming out from it. However, since I haven't yet explained what energy and momentum are, I should probably say something about that first, before going into this.
you are allowed to start with. These constraints are one of the most subtle features of General Relativity, because they ensure that the total energy and momentum of an object (like the sun) are encoded in the gravitational field coming out from it. However, since I haven't yet explained what energy and momentum are, I should probably say something about that first, before going into this.

I always enjoy your blog. I came across another interesting blog post and wonder if you would be willing to write a blog post about this topic to explain it better.
https://www.simonsfoundation.org/quanta/20130917-a-jewel-at-the-heart-of-quantum-physics/
Hi Ron, welcome to my blog.
I would, except that I don't understand what Arkani-Hamad does, although I've seen him give talks about it. But, my impression is this: You have to cut through the wild speculation which excited the journalist, in order to see the actual result.
What he actually did (which is buried in the article) is figure out a much simpler way to calculate the way that gluons (the particles which carry the strong force which binds quarks together) interact with each other. He believes that maybe you could do something similar with gravitons (the particles which carry the gravitational force), and that if you did it would give you a consistent theory of quantum gravity. Like most approaches to quantum gravity, this is very speculative (I doubt he'd disagree with me about this...). We physicists all have our own pet ideas about where the Holy Grail might be hiding, but none of us really know.
Hi Aron I have a quick question. In the Einstein equation you posted above, if the stress energy tensor is 0 at a particular point, does that imply that the curvature must also be 0? I'm thinking, for example, of the schwarzschild metric, where the stress energy tensor only takes a non zero value at the center mass. Does that imply that the curvature (expressed by the Ricci tensor) elsewhere is 0? If so then how is gravity mediated from the center mass to, say, planets orbiting it? I was always under the impression that a massive object not only distorted the space it occupies but also the space around it. Or is that what you were speaking about with the Weyl tensor?
Matt,
Yes. If the stress-energy tensor is 0, the Ricci tensor has to be 0, but the Weyl tensor doesn't have to be. Just as you suppose, this is the reason why gravitational fields can exist even in regions without matter. In particular the Weyl metric of Schwarzschild is nonzero.
Interestingly, if the number of spacetime dimensions were 3, a Weyl tensor would be impossible, and all components of curvature would have to vanish outside of matter. So in that dimension, gravity works completely differently. A point mass produces a "conical singularity" which causes the total angle going around the particle to be less than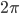 . The spacetime in the conical geometry outside is locally flat everywhere else: you can only tell it's not Euclidean if you circle around the point mass. There would be no attraction between different masses.
. The spacetime in the conical geometry outside is locally flat everywhere else: you can only tell it's not Euclidean if you circle around the point mass. There would be no attraction between different masses.
Aron,
Thank you! Just to be clear then, is the presence of a non-zero Weyl tensor solely the result of gravitational waves? I ask because my understanding of gravitational waves (which could very well be horribly wrong) is that they are the result of the motion of massive objects, and in the case of Schwarzchild, the center mass is completely static. Thus there would seem to be no gravitational waves emitted and therefore the Weyl tensor would be 0. Do massive objects just in general emit gravitational waves? Or are there other factors that contribute to the value of the Weyl tensor? Given that the Weyl tensor is non zero in the Schwarzchild case, does that imply that the geodesics traced out by objects orbiting the center mass are a result of the tidal forces expressed by the Weyl tensor? Thank you again!
Matt,
By definition, a `wave' is a wiggle in a field which oscillates, or at least moves about independently. So when the Weyl tensor is nozero but static (due to being sourced by a massive object like a star) we don't call it a gravity wave. Just like we don't call perfectly still swimming pool a water wave, even though it's made out of water! Now if we start shaking the star, the gravitational field becomes time dependent, and some of the wiggles in the field will propagate out to infinity, in a way which no longer needs to be supported by the star. This type of gravitational field we call a gravity wave.
The exact same terminology is used for electromagnetism. If you have a charged particle/magnet just sitting there, then there is a nonzero electric/magnetic field, but we don't call that a wave since it doesn't wiggle. But if you start shaking the charged particle or magnet, it will emit electromagnetic waves.
But this is really a qualitative distinction designed to help us describe particular special situations. If you have a bunch of masses (or charges) moving around in a really complicated way, it's probably not a very useful or fundamental question to ask "Which part of the curvature is `waves', and what part is `the field' of the masses?" That's a question which you shouldn't ask, since the basic field equations don't draw the distinction between these two `types' of curvature. Locally, they are exactly the same thing.
When geodesics traced out by nearby orbiting objects accelerate relative to each other, that is indeed the Weyl tensor at work.
Hope this clears things up!