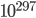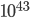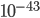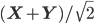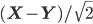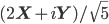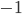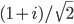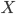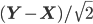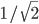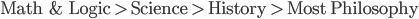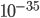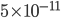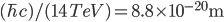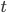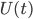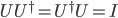A reader, Martin B, asked me a question in response to my review of Krauss' talk on “A Universe from Nothing”. I had written:
"Atheists such as Krauss scorn theology as being completely non-empirical. They claim it is not based on evidence of any sort. I find it extremely ironic when this sort of atheist thinks that speculative quantum gravity ideas are just the right thing to further bolster their atheism. Suppose you think that Science is better than Religion because it is based on evidence, and suppose you also want to refute Religion by using Science. Here's a little hint: consistency would suggest using a branch of Science that actually has some experimental data!”
Martin asks:
But isn't there empirical data that suggests "speculative quantum gravity” is real? It's not taken out of the blue, is it?
Anyway, the problem I have with religion/faith is that it's so arbitrary. Depending on who you ask there are all kinds of idea of what's "true” when it comes to theology. May I ask what it is that makes you think Christianity stands out and is more believable than other religions and faiths on this planet?
I.
It is common for atheists to assert that religion is based entirely on speculation, and that therefore there is "no evidence" for it. Now I don't agree that religion is based primarily on speculation, but I also don't agree that speculation counts as "no evidence". Let me explain.
Speculation, in the particular sense we are considering, is defined by various dictionaries as follows:
- "the forming of a theory or conjecture without firm evidence" (Google)
- "ideas or guesses about something that is not known" (Miriam-Webster)
- "reasoning based on inconclusive evidence; conjecture or supposition" (American Heritage)
In other words, speculation is essentially what you do when you don't know something for sure, so you sit around without guidance and try to figure out what makes the most sense.
Now sometimes when we sit around and think about things, we find a really good reason to think that something is in fact the case. For example, we might find a rigorous mathematical argument. In that case, we would talk about having a "proof" instead of mere speculation.
More controversially, many philosophers have also believed themselves to have deduced certain propositions by thinking about them carefully. The track record for this is not very good, since philosophers can't agree on which things are in fact provable in this way, and some of them have claimed to prove things which later turned out to be false (e.g. Kant thought that Euclidean geometry and Newtonian mechanics were necessary truths!). However, it is plausible that at least some philosophical arguments are strong enough to be considered "proofs". (Even if you are a skeptic about the ability to deduce most truths about the world by philosophical reflection, you probably came to that conclusion by thinking about it philosophically, so there's no escape.) Also, Logic and Probability Theory are sometimes considered branches of Philosophy, and these seem to be on fairly solid footing for most purposes (at least if we ignore the puzzles raised by quantum mechanics).
Be that as it may, normally our experience is that, at least about most subjects, "armchair reasoning" is not very likely to lead people to the truth, unless it is supplemented by some source of data which is based on empirical evidence. Two particular fields of study which do involve large quantities of empirical data, are History and Science. The former is based on testimonies, documents, and artifacts left behind by those who lived in the past, while the latter is based on repeatable observations carefully scrutinized by the scientific method.
I would judge that normally the strength of evidence we obtain from the fields I've mentioned is as follows:
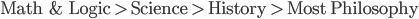
However, this is just a general expectation based on averages; specific cases might turn out differently. As I said before, some philosophical arguments are very strong (e.g. if you don't believe the philosophical arguments that we can learn things about the external world based on observation, you can't have any grounds for believing in Science either.) Math proofs are supposed to be completely certain, but if they are thousands of lines long it is easy for errors to sneak in.
And, in cases where historians or scientists don't have enough strong enough evidence to prove the truth about something they care about, they too will resort to weaker evidence, including (educated) speculation. Just because an argument is made by people who work in a History or Science Department, doesn't necessarily make it non-speculative. You have to look at what (if any) actually supports the statement!
Now, it is clear that educated speculation is right more often than chance would predict. It has often happened that scientists have brilliantly guessed in advance correct theories of Nature, based on partial or incomplete evidence. This is the sort of thing theorists get Nobel prizes for. (If they were guessing based on chance, you'd expect they'd never get it right, since the space of logically possible ideas is huge.) On the other hand, it also often happens that the brilliant conjectures turn out to be completely false. So reasonable forms of speculation do involve a kind of evidence. It's just not a very strong kind of evidence. How strong it is, depends on just how many leaps of conjecture one takes, beyond what is already known.
Therefore, we should not conflate "speculative" with "no evidence".
II.
So when you say:
But isn't there empirical data that suggests "speculative quantum gravity” is real? It's not taken out of the blue, is it?
I entirely agree with you. Quantum gravity isn't an idea which just comes out of the blue with no evidence whatsoever. If I thought that were true, I wouldn't work on it professionally!
We know that Quantum Mechanics is a good description of the world of atoms and other small stuff. We know that General Relativity is a good description of situations in which gravitational fields and/or the speed of light are important. It stands to reason that there must be some mathematical model which embraces both sets of ideas into one, mathematically consistent description. Since the physical world exists, there must be some description of it in situations where both quantum and gravitational effects are important. (I suppose conceivably the description might not involve math and equations, but if not that would be a total surprise in light of previous experience with new models of physics. Normally math is the best language for describing Nature in a precise way.)
So the mere fact that there is such a thing as quantum gravity is not particularly speculative. But most of our specific ideas about quantum gravity are highly speculative. Some reasons for this:
- Dimensional analysis suggests that in order to see actual effects from quantum gravity, we'd have to look at distance scales equal to the planck length, which is about
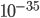 meters (details here if you want the math.). For comparison the Bohr radius (the approximate size of atoms) is about
meters (details here if you want the math.). For comparison the Bohr radius (the approximate size of atoms) is about 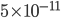 , and the smallest distance scale we've ever been able to probe with the Large Hadron Collider is about
, and the smallest distance scale we've ever been able to probe with the Large Hadron Collider is about 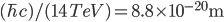 . So quantum gravity is smaller compared to the tiniest thing we can measure, then atoms are to us! So in the absence of some really clever and dramatic experiment, it will be a really long time (if ever), before we have any direct experimental evidence of quantum gravity effects.
. So quantum gravity is smaller compared to the tiniest thing we can measure, then atoms are to us! So in the absence of some really clever and dramatic experiment, it will be a really long time (if ever), before we have any direct experimental evidence of quantum gravity effects.
.
- One could also try to look at what happened in the very, very early universe, but once again this puts quantum gravity earlier than anything we have good evidence for, with the possible exception of inflation (there is decent evidence for inflation, although it is not confirmed for sure; also we don't know whether it happened at the same time scale as quantum gravity or not.)
.
- The attempt to combine quantum mechanics with gravity leads to severe conceptual difficulties, making it difficult to say what we even mean by a quantum spacetime. In addition there are seeming paradoxes which nobody knows how to resolve.
.
- Our current best candidate for a theory of quantum gravity, string theory, is understood well only when the strings are weakly interacting (or when it is dual to certain other theories which don't involve gravity.) In truly quantum gravitational situations, even if we assume string theory is right, we're still in the dark about how to formulate it precisely, let alone calculating what it says. Also string theory, although it has certain very beautiful aspects, is a very complicated construction which includes many elements (supersymmetry, extra dimensions, GUTs, etc.) that have not been confirmed experimentally as separate ideas, let alone as a combined package.
.
- The next most popular candidate, loop quantum gravity, space at the Planck scale is described by a network labelled by numbers, but there is no agreement on how to describe time evolution, nor is is clear whether a continuous-seeming spacetime emerges as we zoom out to larger distance scales.
So the situation is desperate, but for that reason also exciting!
Now the particular idea which Krauss was using, the Hartle-Hawking "no boundary wavefunction of the universe", has in some ways even less evidential support than string theory itself (it certainly doesn't seem to logically follow from string theory, though it might or might not be combined with it). It's just a particularly beautiful proposal for the state of the universe. The best that can be said for it is that it is specific, simple, and elegantly relates the laws of physics to the initial conditions. The worst that can be said about it, is that it may be mathematically ill-defined, and probably contradicts observational data (such as the fact that the universe contains any stuff at all).
So I think I was justified in saying that:
The crucial physics here is totally speculative! It was entirely based on speculative ideas about quantum gravity which anyone working in the field would admit are not proven.
But when I say totally speculative, I don't mean there's no support at all! I just mean really really weak evidence. I'm not trying to bash Hartle or Hawking here, who I'm sure would agree with my assessment. Quantum gravity is hard! We're doing the best we can.
(Commenter St. Scott Church said something similar here.)
But I think it's crazy, if an atheist thinks religion is based entirely on silly speculations, to turn to this as their paradigmatic example of something which is supported by strong evidence. I've also criticized Quentin Smith (a better philosopher than Krauss) for the same offense.
III.
Now let's talk about religion.
On this blog, I've discussed before certain philosophical arguments for Theism, which I think are pretty good, so far as armchair reasoning goes. But I don't think that the strongest evidence for religion comes from this source, and indeed I had a huge long disclaimer at the beginning of that series in which I said so.
What these philosophical arguments point to, in my opinion, is something like Ethical Monotheism, which is sort of the lowest common denominator shared by traditions as diverse as Judaism, Platonism/Stoicism, Christianity, Islam, Sikhism, Baha'i, certain sects of Hinduism, and Deism. (So believing in Christianity does not require that you think everything about other religions is false and misguided.)
But it's clearly impossible to prove something like Christianity from purely abstract philosophical arguments, since it involves a lot of particular doctrines about Jesus (particularly the Trinity and Incarnation etc.) which are much too specific and weird to derive by philosophical plausibility arguments. (Is this similar to what you mean by saying religion / faith is "arbitrary"?)
Instead, I would say that the primary reason for believing in Christianity comes from History—although some elements of philosophical reasoning and personal religious experience come into it as well. I said above that History was based on collecting testimonies and documents from past eras. And this is what the New Testament is.
The primary event on which the Christian faith is based on is the Crucifixion and Resurrection of Jesus. (Followed by his Ascension into heaven, and the giving of the Holy Spirit at Pentecost in order to start the Church.) These events were observed by normal human beings like us, using their ordinary sense data. Those people are no longer alive, but they left behind documents, collected in the New Testament, which describe the teachings and miracles of Jesus Christ and his Apostles (those who were the eyewitnesses to his Resurrection, listed by St. Paul about 20-25 years after the event here, although he omits the women who first went to the empty tomb and were the first to see Jesus, as described in the Four Gospels.)
Now whatever the New Testament is, it is not philosophical speculation. (I will get to other religions in just a moment.) Various of its documents clearly claim to be the records of people who literally saw supernatural events with their own eyes. It could be lies, or some sort of mistake, or perhaps legends which grew up later (although I find all of these theories implausible for various reasons, in part because of the large number of claimed eyewitnesses and in part because the claims arose so early and clearly in the development of the religion). What it certainly is not is a bunch of philosophers, theologians, and mystics sitting around meditating on the nature of the universe and trying to figure out what makes sense to them.
As I have argued before, type of evidence in question (muliple written claimed testimonies) is considered by historians to be strong evidence whenever it supports non-supernatural events, for example the Assassination of Julius Caesar. (Indeed, ancient history would be basically impossible without it.) The quality of the historical documentation compares quite favorably to that supporting similar events at around that time and place. So unless we have a strong prejudice against the supernatural—or have some other specific reason to disbelieve it—we should believe it.
(And, incidentally, you should not have a strong prejudice against the Supernatural, among other reasons because of the abundant documentation of miracles which have occurred in more modern times.)
I argued above that History is, in general, more reliable than Philosophy. For this reason, I would argue that the accounts of the Resurrection of Jesus are more evidentially important than things like e.g. philosophical arguments for Materialism / Naturalism, arguments about how a good God could allow evil in the world, and so on. Those things are speculation, this is data.
Of course, once you accept the Christian data-points, recorded in the New Testament, you still have to do some philosophical/theological analysis to figure out exactly how to explain the extraordinary event. I'm not claiming that e.g. the doctrine of the Trinity was directly observed by human beings. Instead people had to work through the facts (e.g. Jesus claims to be divine in some way and this is backed up by his ability to do miracles; but he also prays to God as the Father, and accepts the Jewish teaching that there is only one God; then he promises to send the Holy Spirit to live in the hearts of those who follow him, who also seems to carry the authority and power of God) and when they worked everything out they had the doctrine of the Trinity. Using the language of Science, this is a theory rather than a fact, but it is a good theory because it is the simplest explanation of the facts in question. (Of course atheists and members of other religions will generally deny that the facts were as the New Testament claims, but that is a completely different question than whether the reported facts support the theory. Just as, if there is controversy over whether a scientist falsified his data, this is a separate question from whether the data, if true, supports the theory.)
I don't want to give the impression that Christianity is only about stuff that's happened in the past: Christians also believe that the Holy Spirit is present in believers, in order to guide us into the truth and to form in us the kind of loving character that Jesus had. Some Christians have also had few dramatic communications from God or other mystical experiences, but this is quite secondary compared to learning to live life together as a holy community of people. Once you come to believe it is true, then faith is indeed necessary to continue along the path even when nothing much seems to be happening.
Religion is about the encounter of the soul with God. It seems clear that most people don't come to faith by robotically analyzing the evidence (or to disbelief, for that matter). But I still think people should carefully consider the evidence when deciding whether to believe. It is important to check that one is not being deceived by something false.
IV.
May I ask what it is that makes you think Christianity stands out and is more believable than other religions and faiths on this planet?
Gladly. When analyzing a religion for truth, I would ask questions such as these (none of these criteria are necessarily intended to be definitive when taken in isolation):
- Has the religion persuaded a significant fraction of the world population, outside a single ethnic group, to believe in it?
- How does the religion relate to previous and subsequent religions?
- Did the religious founder claim his message came from supernatural revelation, or is it only the reflections of some wise philosopher who didn't claim to have divine sanction for their teaching?
- Are the primary texts describing some sort of mythological pre-history, or are they set in historical times?
- Related, does it sound like fiction, or does it sound like history?
- How long was it between the time when the supposed supernatural events took place, and when they were first written down (in a document that has had copies of it preserved). Is it early enough to suggest the text is based on testimony rather than later legends?
- What are the odds that the purported supernatural events could have occurred for non-supernatural reasons?
- Did the main witnesses benefit materially from their testimony, or did they suffer for it?
- Is there significant evidence of fraud among the originators of the religion?
- What is the general moral character of the religious teaching?
- Do people who are serious about this religion generally feel that they are put into an actual relationship with the divine?
In a future blog post, I will try to provide my own personal answers for how well various religions satisfy these criteria, and why I think Christianity is the most convincing case of divine revelation that has occurred. However, I've included these questions separately from my answers, in order to encourage you to think about them on your own.
Sometimes I meet people with a sort of learned epistemic helplessness, just in the area of religion. The attitude is: well, group A claims this miracle, and group B claims this divine revelation, and I am completely at a loss and unable to even begin to say which claim is more plausible! Therefore I won't accept any of them.

Yet when it comes to less important matters in their everyday life, they are perfectly able to use their brain to decide what is credible and what is not. If you really want to know what is true, I'm convinced you are able.
Look, and maybe you'll find. Ask, and you might just get it. Keep on knocking at that door, without giving up, and—if there's anyone on the other side—surely it will be opened to you.