A reader asks:
After a lot of reading, I've come to realize that the Bayes factor for the resurrection is quite high that if the event in question wasn't a supernatural occurrence, no rational person would think that the event did not occur. However, I've stumbled upon an argument by a philosopher who argues against the resurrection argument by using bayes theorem as well.
I've included a link of a debate where he presented his arguments in a long mathematical form in case you wanted to refer to it, but the gist of his argument is that the prior probability of God raising Jesus from the dead is always going to be magnitudes lower than that of God *not* raising Jesus from the dead. He is a theist himself, so he argues that he does't follow Hume in his argument against miracles, but rather he claims to be making an argument from natural theology: Every experimental confirmation of a scientific theory that we observe counts as evidence of the fact that God created and ordered the world in an orderly and causally closed way and does not intervene. In another presentation, he puts forth a statistical inference of this sort(I didn't copy and paste it so it might be a flawed syllogism, but I think it captures the gist of what he's saying):
(1) For every dead person, 99.9999...% of the time God does not intervene
(2) Jesus died
(3) Therefore, we can be 99.9999....% certain that God did not intervene in Jesus' death
He argues that for every instance of a "miracle" being reported, we have experimental confirmations of the laws of nature of a much higher frequency. So, he concludes from all of this that the prior probability that God would raise Jesus from the dead is so astronomically low that however high our Bayes factor is *for* the resurrection, the prior improbability of God wanting to intervene with the laws of nature is always going to be much higher such that the posterior probability (or final probability) of the resurrection is always going to be really low.
This argument is unlike any other because it doesn't assume naturalism, in fact it assumes theism. It doesn't assume that God cannot or could not have raised Jesus from the dead, but that it is highly improbable that God would have intervened.
As a scientist, what do you think of this argument (Since your career involves seeing confirmations of God's love for order in the universe everyday?)
https://www.youtube.com/watch?v=XCCmDqQ7qgI
[Dr. Robert Cavin vs. St. Calum Miller](He presents his argument from the 14th minute to the 30 minute mark)
What do you think of this argument?
(1) For every American citizen who lives during a presidential election, 99.9999...% of the time they do not become President.
(2) St. Barack Obama was a living American citizen in 2008.
(3) Therefore, we can be 99.9999....% certain that Barack Obama did not become President of the United States.
Clearly there is something wrong with this argument. What's wrong with it is that Obama is not a randomly selected [or typical] citizen. He belonged to a special class of people who is unusually likely to become President (a Senator, a charismatic speaker, wanted to become president, went on to receive the nomination of a major party...). Since we have additional information, it is fallacious to use the background rate to decide the chances of him becoming President. [And of course, we also have excellent posterior evidence, coming from the period after the election, that he did in fact become President.]
In the same way, Jesus is not a randomly selected human being. He was a person who claimed to be the Jewish Messiah and the Son of God, fulfilled certain prophesies, did other miracles, and so on. So the prior probability that God will dramatically intervene shortly after Jesus' death, is a lot larger than the probability that he will dramatically intervene when one of my uncles dies. (Although, actually God DOES plan to raise 100% of human beings from the dead when Jesus returns, the difference in the case of Jesus is that he did it right away.)
The reasonable question is, what is the prior probability that God would make some special person to be the Messiah and raise that person from the dead? (Just like, we could ask what is the probability that any person becomes President.) Once we believe that somebody is going to be President, or that somebody is going to be the Messiah, we shouldn't be all that surprised to learn that any one particular person turns out to be President, or the Messiah, so long as they are qualified for the position.)
The argument in the video is even more fallacious. First of all, I should say you should be VERY SUSPICIOUS of any person who starts their argument by making concessions that huge to the other side. Factors of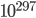 
are ridiculous numbers that should never be thrown around in almost any real life situations, and if he concedes something that ridiculous to his opponent, he ought to be guaranteed to lose, plain and simple. He's like a stage magician who makes a big show of how he's blindfolded and his hands are tied behind his back and so on. You can be very sure there's a trick somewhere, and that all that patter is there to distract you from the way he actually does the trick.
(The other guy, St. Calum Miller, is also making a fallacy, when he quotes a liklihood factor of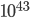 
for the Resurrection; this number incorrectly assumes that the evidence from each apostle's testimony counts independently. The odds of a group conspiracy to lie are certainly bigger than 
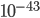, which is an astronomically tiny number. No real historical event is ever that certain. That being said, he's right that the evidence for the Resurrection is extremely strong, as far as historical evidence goes! It's just that nothing in life is really that certain.)
By the way, Cavin is derisive about St. Craig Keener's statement that there are a hundred million miracle reports, but this is not actually all that silly of a number. If 2% of the world's population claims to have seen a miracle, that's 140 million right there, assuming none of the events are redundant. So I don't think this claim can be dismissed quite so easily.
Anyway, in his argument, Cavin compares the likelihood ratios of L (the laws of nature are always valid), M (at least once, God acts miraculously), and ~(M v L) (neither one is true). The last comes in because L and M are not exhaustive, since there might be neither laws of nature nor divine interventions.
The actual fallacy in his argument is displayed on the slides at the 33:45 mark of the video. He claims that ~M (i.e. not M, which would include both L and ~(M v L)), because it is maximally unspecific and does not necessarily predict that there are any laws of nature at all, is disconfirmed every time anything happens in accordance with a natural law. Then he claims that M, because it only adds to ~M the claim that at least one miracle happens, is at least as bad off as ~M!
But this is clearly quite absurd. Not even the most ardent believer in the supernatural thinks that every time I drop a ball, there is a 50% chance that it will miraculously fall up instead of down. Not even the most tempestuous skeptic really halves their chance that God does miracles, every single time they see a ball drop!
Obviously, miracles don't happen all the time. What Christians actually believe is:
M': the usual laws of Nature are almost always valid, but on rare occasions (especially at important moments in salvation history) God intervenes to perform miracles.
(By important moments in salvation history, I mean things like: critical events in ancient Israel, the ministry of Jesus and the Apostles, times when missionaries preach the Gospel to a group of people for the first time, or sometimes for the conversion of a particular individual. Aside from this, sometimes God heals people in answer to prayer and so on, but my point is that miracles are not randomly tossed into history like darts shot into a dartboard; they tend to happen in specific kinds of situations.)
Now M' clearly does predict that balls will normally fall down. So it is just as good as L (the laws of nature always hold) for purposes of everyday life. So his huge probability factor of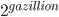 
goes away. But M' is better than L in situations like Jesus' ministry, where there is significant historical evidence that miracles really occurred.
Incidentally, this implies that he was quite wrong to rank the probability of ~M (no miracles) so low. Even though it is a very unspecific hypothesis, we shouldn't consider randomly selected examples of ~M, instead we should focus on whatever are the most plausible versions of ~M. And clearly, the most plausible versions of ~M are scenarios where the laws of nature are followed, at least most of the time. In fact, the most plausible version of ~M is L. Thus he is guilty of a clear-cut violation of the laws of probability theory here, since he simultaneously argues that ~M is very improbable, and L very probable, even though L actually implies ~M! This is an example of the Conjunction Fallacy:
https://en.wikipedia.org/wiki/
Had St. Miller realized this, he could have totally eviscerated Cavin's argument in a couple seconds, in a way that would have been completely humiliating and decisive. However as far as I can tell (I skimmed through his remarks very quickly) he mostly just ignored that argument and presented the positive case for the Resurrection.
Similarly, the most plausible version of M is not a scenario where God intervenes half the time we do a science experiment (I agree THAT is ruled out), instead it is a scenario along the lines of M' or similar.
To give another illustration, consider the famous proposition
W: All swans are white.
For a long time, Europeans noticed that every swan they ever looked at was white. You could take this as huge experimental confirmation for W. Every time you look at a swan, W predicts it is white and therefore is confirmed by a factor of at least 2 over ~W (and that's if there was only one other color besides white), which says the swan could be any color. Since there were millions of observations of white swans, doesn't this mean that W is a gazillion times more probable than ~W?
And yet, there are black swans!
https://en.wikipedia.org/wiki/
The fallacy is to assume that the most plausible version of ~W is that each individual swan's color is random. In fact all the swans in Europe are white; the black swans are not only rarer, they live in Australia. So it is no surprise the Europeans didn't notice them until they came to Australia. So actually ~W was almost as good of a theory as W, aside from being slightly more complicated.
As a scientist, what do you think of this argument (Since your career involves seeing confirmations of God's love for order in the universe everyday?)
That is indeed the exact point. We worship a God who loves order, and therefore he does not do miracles haphazardly. No scientific experiment can ever be evidence against miracles, unless you have some theological reason to believe that God would have been likely to intervene in that particular experiment. For most experiments, the opposite is true—it would frustrate the ability of his creatures to learn about the world, without providing any particular benefit.
(I am assuming here that the goal of the particular experiment was not specifically to look for evidence of God, as in e.g. prayer experiments. In that case, we all know that God does not usually respond to challenges to show his existence by striking a nearby tree with a lightning bolt. The fact that he doesn't do that may be evidence against a certain sort of deity, but even there I don't see what is gained by dressing up the challenge with a veneer of science, when the whole point is simply to challenge God to act.)
Note: I only answered this question as a special favor to the particular reader in question. I hate watching long web videos, and I tried to watch as few seconds of this one as I possibly could, to answer the question accurately! I much prefer to interface with texts, which can be read at the speed I want, and then quoted accurately using the copy-and-paste function!
[Edit: In an earlier version of this blog post I misspelled the name "Cavin"; I apologize for this mistake. Also, I would like to make it clear that, except in the portions of this blog post where I respond directly to the video debate, I am responding to the arguments as presented by my interlocutor, without asserting that it is necessarily an accurate summary of Cavin's position.
A few other changes made after the fact are in square brackets.]
Hi Aron, I really appreciated this thanks. I am interested in these questions too, and I'm not sure if I would ever have thought of the Barack Obama argument you begin with, but it is an excellent illustration.
PS I too prefer text to videos so I can skim and quote easily.
It seems to me there's more going on here than a misapplication of some probabilities--neither of these guys appears to understand the basics of Bayesian probability. What we're interested in is whether Theism (T) or Naturalism (N) is more probable given the historical evidence for miraculous events (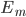
) and our background knowledge (b). That is;
T and N cover all reasonable possibilities so they'll be normalized to each other (N = ~T). This reduces the relevant factors in the calculations to the probability of observing at least one miraculous event given T and the background information, and that of observing it given the background information alone;
The first mistake made was to bring L into the discussion in the first place--or more precisely ~(M v L). Bayesian probability allows us to determine the likelihood of a hypothesis from evidence and priors where by prior we mean the background (b). By definition, b is information that's already a given in either outcome--not a set of any "maximally unspecific" scenarios we can dream up. Trying to pass off ~L as part of a "prior", and L as "evidence" for N is fundamentally wrong-headed. ~L cannot be a prior because it is not a given--no one, theist or atheist, has ever lived in a universe like that! In the real world--the only one that concerns us--L is a prior to T and N. It is most certainly not evidence for N.
The second mistake was his attempt to define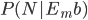
in terms of the number of times God did not intervene to resurrect anyone dead person in history. Why base that estimate on just anyone who has died? For that matter, why base it on any human? Why not consider whether God would be likely to resurrect some kid's pet frog? What we have here is a textbook example of the reference class problem in probability. The very idea of trying to put a numerical estimate on God's motives for intervening miraculously in His creation takes presumptuousness to a whole new and terrifying level.
In probability analysis it is absolutely crucial to understand the difference between evidence and priors, and base the former on meaningful reference classes. Otherwise, the whole exercise becomes an elaborate justification of one's prejudices. Science and philosophy alike are littered with the wreckage of failed attempts at both, and this is yet another case in point.
Couldn't that argument just as easily be used to argue against the 'resurrection as legend' view?
(1) 99.9999...% of people that have ever lived have not been legendized so quickly and completely that within several decades of their death, they were transformed from an ordinary person into one who regularly performed miracles of all kinds, and was ultimately resurrected from the dead*.
(2) Jesus was a person who lived.
(3) Therefore, we can be 99.9999....% certain that the miracle and resurrection accounts of Jesus are not the product of extensive legend that developed within several decades of his death.
* I know people argue that there are other miracle workers and resurrected beings in history, but they are very inadequate parallels for more than one of the following reasons: (1) the miracles stories did not develop within decades (if they can be traced to a historical person at all); (2) the miracles are frivolous, rather than meaningful; (3) they occurred in private; (4) they were limited in number, nature and/or circumstances; (5) they did not include resurrection; (6) they did not lead to the belief that the person who performed them is the Son of God who died for the world's sins, igniting a radical movement.
Pingback: Two scientists, probability and God
Is it reasonable to apply the probability theory to miracles in the first place?
For "any given miracle is a strictly individual event that cannot be expected to occur again" (Miracles and Physics, Stanley Jaki).
And given the verification of miracles essentially involves historical method, ancient miracles as objects of historical investigation are a much more difficult matter than recent miracles such as miraculous healings at Lourdes and the miracle of the sun at Fatima.
As a non-sectarian person myself, I observe a strange reticence that Protestants exhibit when confronted with the evidence of Catholic miracles e.g. a Marian vision that commands the believer to pray the rosary or names herself Immaculate Conception. This Protestant reticence is analogous to the reticence that atheists and other non-believers show when confronted with New Testament miracles. It almost appears that the Protestant would prefer the Marian miracles to disappear .
And yet, evidence for the Marian miracles is not less than New Testament miracles. The body of Bernadette Soubirous still lies incorrupt in a glass casket in Nevers.
Scott,
Roughly speaking I agree with you about where he went wrong, but
(i) by L he means to exclude the existence of any miracles, so that is not the right prior to consider. It should be something more like what L and M' have in common.
(ii) I would say that when you select your priors in Bayesian probability theory, in principle you can go back as far or as little as you like. If you want your prior to depend only on a priori factors plus observations you made before you were 13, and then to update based on the likelihood of everything you have learned since then, you could do that. In principle if you did the calculation correctly, you should get the same answer no matter where you put the cutoff, since it's just a matter of moving things between the "prior" and "liklihood" categories. However, this could be so complicated that would be impossible not to make mistakes in practice. In practice, to make things as simple as possible one should normally assign priors based on everything you knew before some specific measurement (whichever measurement is the controversial new piece of data you wish to consider the effects of).
i like pizza,
Yes, you could equally well turn the argument around that way (and it would still be fallacious, even though in this case it points in the direction of the correct conclusion). Fallacious arguments can generally be recognized by the fact that they "prove too much", that similar arguments could be used to prove almost anything (right or wrong).
I like your list of inadequacies, especially (1-4). (5) is evidentially relevant to the extent that resurrection miracles are more difficult to fake. (6) seems to just be a rephrasing of Christian belief, so it seems to be begging the question a little to say the other miracles are different because they don't involve that.
It's worth pointing out though, that even if there are false miracle claims which are to some extent parallel to the Christian ones, so long as such miracle claims (both true and false) are rare, they still provide significant evidence for the Christian faith. Just as, the existence of a few dozen false claimants to be the Messiah does not change the fact that a Messiah-claimant is significantly more likely to be the Messiah than a randomly selected one of the billions of non-Messiah-claimants. By itself this could not possibly prove that Jesus is the Messiah, but as part of a cumulative case which includes other factors that distinguish Jesus, it can still pull a lot of weight.
Mactoul,
As a Bayesian, I think it's reasonable to apply probability theory to anything, including individual events which do not recur.
All else being equal, I agree that recent miracles are easier to confirm than ancient miracles, due to the greater ability of contemporary observers to access the evidence. However, all else is not always equal, and in particular I would argue that the Resurrection of Jesus (which is of course fundamental to all branches of Christianity) has many unique features that make it exceptionally convincing.
Nevertheless, I do take your point that it can be strange when Protestants (who believe in miracles) analyze Catholic miracles with the same degree of suspiciousness that atheists apply to biblical miracles. In fact there is something of a historical relationship between the two sets of arguments, mediated through Hume.
When one argues with an atheist or an agnostic, one has the option to try to safeguard their beliefs by retreating into a pit of arbitrarily bottomless skepticism. In some ways it is more fulfilling to talk to Catholics (or Muslims) since in this case both parties believe something concrete, and so the allowed moves are restricted since one cannot cut off the branch that one is sitting on. Never having been an atheist myself, it is an interesting experience to argue with Catholics since it conveys the experience of arguing with somebody who (in some senses) believes in "more" things than I do.
(To set a good example for the atheists:) Although I am a Protestant, I do take Catholic miracle reports seriously, and consider (some of them) to provide noteworthy evidence for Catholicism. Just not enough evidence, in my opinion, to overcome the implausibility of certain specific Catholic interpretations of the Bible. (I do not of course mean to imply that all Catholic doctrines are implausible, but since this church claims to be infallible, they have to get them all right to be correct. To me, Protestantism should not consist of the knee-jerk rejection of everything Catholic, but rather is simply the assertion that no particular church is infallible.)
Since I already believe that God is willing to do miracles on behalf of Christians even when they get some points of theology wrong (as we probably all do), Protestantism is perfectly compatible with believing that many Catholic saints have done miracles. (And I think there is plenty of good evidence that they have.) Of course a lot of Catholic healings happened after invocations to saints, a practice rejected by most Protestants, but presumably most of those individuals also prayed to God so this is again not necessarily inconsistent with Protestant theology. The issue arises with miracles which support in some way particular Catholic doctrines that Protestants do not believe, including for example Marian apparitions.
Having said all this, one has to analyse each miracle on a case-by-case basis to evaluate its historical and theological plausibility, and I think there are good reasons to be skeptical about many of these miracles. For example, staring at the sun is actually very dangerous and it is not surprising that many people in the crowd saw a variety of unusual visual phenomena afterwards (there were also many people there who saw nothing.)
That the bodies of certain saints appear incorrupt is an empirically observable fact, but it is not completely obvious to me that it cannot be caused by natural causes, for example placing the body in an airtight compartment with unusual conditions, or perhaps some emblaming procedure done to the body beforehand. The vast majority of saints' bodies decay just like anyone else's, so whatever physical conditions involved would only have to be in operation a small fraction of the time. I admit that I have not investigated this phenomenon very closely and am speaking from ignorance. But it is not so clearly impossible as e.g. Jesus' resurrection, or giving sight to a man born blind.
I have looked into a number of Marian apparitions and felt there to be something off about their atmosphere. When Jesus appears to a Catholic or a Protestant in a vision, he often speaks with the same heavenly voice of authority that is recognizable in the Gospels. But when Mary speaks to a Catholic in a vision, I do not recognize her as being the same Mary I read about in the Gospels. The St. Mary who wrote the Magnificant was humble but fierce; the Mary who appears in apparitions is mild but lofty, which is nearly the opposite. It is almost as if the details of the Gospel records, not being found quite adequate, have been filled in with a maternal Jungian archetype. (The personality of Jesus in the Gospels is no Jungian archetype.) Instead of speaking words of heavenly consolation that cut to the heart, she generally offers some sort of trinket.
Also, isn't "I am the Immaculate Conception" borderline blasphemous, given the pretty clear allusion to the "I am" sayings in the Gospel of John? Neither Catholics nor Protestants believe that Mary is the divine being, the one who says "I am who I am" from the burning bush. (Leaving aside Jesus' effort to discourage Marian devotion, and the apparent contradiction with St. Paul's teaching, that "all have sinned and fall short of the glory of God" (Romans 3:23). Of course the New Testament also indicates that Christ was an exception, but it does not indicate the existence of any additional exceptions.)
(Don't even get me started on the Brown Scapular or Medjugorje!)
That being said, the evidence for some dramatic healing miracles at Lourdes seems to be fairly strong. I think I conclude that God is a lot less scrupulous about handing out miracles to people with any kind of faith in Christ, than I might have expected him to be. So it goes.
Aron,
Re: our discussion of incorrupt bodies of saints, there is a news about "the incorrupt body of Archbishop Dmitri of Dallas. He died in the summer of 2011, and was buried unembalmed, according to Orthodox tradition. On Friday his body was disinterred for transferral to his new tomb in St. Seraphim Orthodox Cathedral in Dallas, which was his own. When the cemetery personnel opened his coffin, they found Vladyka Dmitri incorrupt".
From theamericanconservative.com/dreher/dallas-saint-dmitri/
[I moved this to the correct post, and made the link active.--AW]
Mactoul,
Thanks for the link. I can't help but notice that only the hands of St. Dmitri are showing, and they look kind of shrivelled and discolored. Admittedly, he was 88 when he died, so it's conceivable they looked like that while he was still in this life. Hard to me to say given that I didn't know him personally.
One individual in the comments of that article suggested that, since his body was placed next to dry ice in order to keep it cool during the funeral, that this might have effectively freeze-dried the corpse leading to it's unsual preservation. Some one else said that corpses can remain reasonably intact for 7-10 years if buried in certain conditions. (I don't suppose it's at all likely that any morticians are reading this blog and can comment?)
So I think it would be a bit hasty to conclude that a miracle must have happened here. Of course, none of this detracts from the testimony that he was a remarkably kind and loving person, which is a far more important work of the Holy Spirit. I'm not sure it came across very clearly in the article, but I've known someone in my own life who is so intensely holy and loving that it is almost palpable. It makes one realize why artists draw saints with halos around their heads.
Regarding the case of St. Bernadette, this article says that:
This does not quite match my intuitive notion of what "incorrupt" means.
Pingback: A foolproof argument against the resurrection?
Hi Dr Wall (and the rest!), I had another curious thought about probabilities and the resurrection that I was hoping I could get some help with (more like a clarification).
Historical knowledge seems to be all about probabilities. The usual step to show that the resurrection most likely happened is by an abductive argument from these four historical claims:
1) Jesus died by crucifixion (p=0.9)
2)Jesus was buried in a grave by Joseph of Arimathea (p=0.7)
3) His tomb was discovered empty by the women disciples (p=0.7)
4)The disciples claimed to have experienced the physically risen Christ (p=0.9)
I added estimate probabilities to the truth of these historical claims as some of these facts are far more certain than ther rest. If I multiplied the probabilities, it would give me a value of <0.5, so would this mean that the probability that all of these are true at the same time is less probable than not?
I'm pretty sure I'm wrong though. But it sounds intuitive to me because say we have two factual claims
(1)I have Gene X (p=0.51, more probable than not)
(2)People with Gene X will get get disease X (p-0.51)
It seems obvious to me that the conclusion of these two factual claims is not that it is more probable than not that I will get disease X. It seems reasonable to believe in both the premises (i.e. to believe that I have Gene X and that people with the Gene will most likely get the disease), but the conjunction of the probabilities are still less probable.
Declan,
The reason you're getting confused is that you aren't doing a proper Bayesian analysis. A proper Bayesian analysis requires that you first identify the various hypotheses which could explain the events (e.g. Naturalism (N) vs. Christianity (C), etc.). Then you have to figure out the prior probabilities of each hypothesis, and the likelihood of each piece of data on each hypothesis (and the preceeding pieces of data).
Multiplying the probabilities of 1-4 is only a valid technique if the probabilities are all independent. But that is not applicable to this case, because the probability of 1-4 occuring will depend on whether N or C is true. Additionally, it is not possible to estimate the probabilities of 1-4 in a neutral way without reference to whether N or C. (In particular, 3 & 4 are a lot more likely to be true conditional on C, then if N is the case.)
So what you really need to do use Bayes theorem to evaluate P(C|1'2'3'4'), where 1' is the evidence that 1 is true, 2' is the evidence that 2 is true, and so on, and when I write two propositions next to each other I mean the conjunction of all of them. This calculation could get somewhat messy since in principle you could have any combination of 1-4 being true at intermediate steps; there are various ways to expand it out depending on what you assume is independent, but one formula which is always true is
You can see from this expression that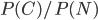
could end up being very large if any one of the ratios in question is very large, for example if Naturalism has a hard time explaining one of the facts 1', 2', 3', 4'.
Anyway, I'm not expecting you to actually calculate all of this out. I just wanted to give a sense of the gap between what you are doing and what an actual Bayesian calculation would look like.
Now let me make a couple more miscellaneous points:
A. In addition to assuming independence, you also seem to be assuming that if any of 1-4 fails, that Naturalism wins. But this isn't so obvious. In particular, both 3 and 4 are low probability events given N & 1 & 2. (And 4 is low probability given N & 1 alone.)
B. In addition, I think your probability assignments of 1-4 are much too low. The reason is that each one of them is supported by multiple different pieces of evidence. There is a reason why (as St. Gary Habermas has pointed out) there is a virtual consensus of New Testament scholars on 1 & 4, while a majority accept the empty tomb (with those who do not, presumably being motivated by strong naturalistic presumptions).
So .9 is too low and .7 is MUCH too low. If you replace these numbers with .99 and .97 you'll get a very different answer! (And honestly, I think .99 is still an underestimate for 1 & 4.)
C. In your disease example, multiplication of probabilities is only acceptable if (a) there is 0 probability of getting the disease if you DON'T have gene X, and (b) there is no other evidence either way about whether or not you have the disease (for example, symptoms). If there is additional evidence, then in general 1 & 2 will no longer be independent.
Ah, I also asked a friend who was doing actuarial science this question and he told me that I was assuming independence as well.
My original intuition was that, regardless of the Bayesian analysis, because I multiplied the probabilities, then it implies that it is more improbable than not that all four facts are true. Which lead to odd results when I applied it to other stuff in life.
Anyway, why would 70% be too low an estimate? I just listened to a debate between Bauckham and Ehrman about the reliability of the NT, and realized that there are some facts more certain than others. The burial accounts seem to be true on a more probable than not basis since, unlike the crucifixion, it's established through use of the traditions reported in the gospels, which most likely had a historical core, but it's hard to be very certain here. Aren't values like 0.99 and 0.98 near levels of absolute certainty?
and thanks for the very speedy reply!
Declan,
Of course some facts are more certain than others. I never denied this!
But 70% is pretty close to 2/3, so that the odds are only twice as good that e.g. the burial happened than that it didn't. That seems extremely suspicious for an event mentioned by four different near-contemporary historical sources (not counting the corroborating statements in Acts and 1 Cor 15). Admittedly the sources are not independent, but they do contain some material unique to that author, suggesting each had their own source of knowledge.
Honestly, I think 70% would be too suspicious for an event supported by a single source. When you read a secular history book, do you really assume that 30% of everything you read is false? (Even that understates the comparison, because if you assign 70% to an event supported by multiple alternative sources, you would have to be even more suspicious of the things supported by only one source, or circumstantial evidence.)
Even if we do assume that each Gospel author had a 30% chance of writing down something mistaken, if we naively multiply the odds of them all being mistaken, we get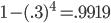
. That assumes that all 4 Gospels are independent, which is obviously untrue, but surely the odds of multiple documents being mistaken should still be considerably less than the odds of 1 document being mistaken. Even if we only count the synoptics as one source, that still gets us to 
.
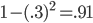My point is it's unfair to multiply the probabilities of 1-4, while ignoring the fact that 1-4 is each in turn supported by multiple pieces of evidence, whose probabilities must also be multiplied! In reality, multiplication is not quite correct in either case due to lack of independence... one should really do a Bayesian analysis involving conditional probabilities, in the way that I said, and not naively multiply probabilities.
Incidentally, I don't think of .98 as near absolute certainty. In physics we routinely deal with probabilities much higher than that. If I were on a jury in a felony case, and I thought there was a 2-3% chance that the culprit didn't do it, I would not consider that "beyond a reasonable doubt" and would vote to acquit. And if there were a .02 probability of a plane crash every time I flew, I'd be dead by now.
Hey Aron,
Long time lurker here. I love your site and the work you do. I would have stayed lurking longer, but I decided to comment because I happen to be writing my own argument for the resurrection over on my blog(http://www.naclhv.com/2016/03/bayesian-evaluation-for-likelihood-of.html).
Specifically, I'm also getting likelihood ratios around 10^43 from my own calculations, and I thought they were quite reasonable - very conservative, even. So I thought that I'd run that value by you again, as someone whose opinion I highly value.
You mention that numbers like 10^43 or 10^297 are ridiculously large and should not be taken seriously, especially in historical settings. I would, in general, agree with you - but there are exceptions to this rule in some kinds of math, and probabilities is one area where such numbers are not uncommon. Here's how I'm thinking about this:
Let me give some examples from probabilities inherent in everyday objects. The probability of shuffling a deck of cards to a specific order is about 10^68. The probability of recreating a game of chess through random play is about 10^120.
Even in physics, 10^43 would be a ridiculously large number if we were talking about something like time (is that in seconds or years? It doesn't matter - it's basically "forever"). But in the branch of physics that deals with probabilities - that is, in statistical mechanics, 10^43 is nothing.
For example, the standard molar entropy of water vapor is 188.8 J/K/mol. So the number of microstates for a mole of water vapor at standard conditions is e^(188.8/k_boltzmann) - that is, about 10^(10^25). Lest anyone think that this is so large only because we're talking about one mole of something, even if we take the moleth root of this number we still get about 10^10 - so, even just five molecules of water vapor will have something like 10^50 microstates.
Also, you mentioned that probability values like 98% are actually not at all extreme. I also think that as well. But the five sigma probability of about 10^-6 is also not all that extreme - it corresponds to something that we're barely certain enough to publish on, at the cutting edge of science. Several independent verification at the 10^-6 level would easily bring the overall probability to something like 10^-43, and any well-established scientific laws would easily break 10^-100, by a large margin.
So, even in history, I can easily imagine a statement like "The Roman Empire existed" having an odds of 10^300 for being true. Basically, my rule of thumb is that probabilities or odds are not "too large" unless their logs are "too large". This makes sense, given the multiplicative nature of probability.
So, I'd love to get your feedback on this way of thinking about probabilities. It forms an important part of my argument for the resurrection, and I'm always looking to refine my ways of thinking.
Thanks in advance for your reply, and thanks again for the work you do here!
"So what you really need to do use Bayes theorem to evaluate P(C|1'2'3'4'), where 1' is the evidence that 1 is true, 2' is the evidence that 2 is true, and so on, and when I write two propositions next to each other I mean the conjunction of all of them. This calculation could get somewhat messy since in principle you could have any combination of 1-4 being true at intermediate steps"
Hi Aron, wouldn't it be easier to do the Bayesian calc on #1, then use the result as a new prior and evaluate #2, then 3, then 4? That would be how you would do it if you discovered these facts over a long time and kept updating, would it not? Or have I misunderstood Bayes??
Eric,
What you said, and what I said, boil down to the same thing. I agree that your way of stating it is a little more intuitive, but if you try to write it out as an equation you'll get some equivalent expression.
Hi Aron, thanks for your answer. But the extra value in doing it "my way", if it is correct, is that we don't need an extra formula, just the normal Bayes formula applied several times. Is that correct? (I am asking because it is a long time since I studied any statistics and I may easily be wrong.) Thanks.
Eric,
Yes, that's right, although the long formula I wrote down is just the Bayes rule substituted into itself several times. So really it's all just different ways to describe the same thing.