This is a new feature which I'd like to try out. I will ask a question about concepts in theoretical physics, and the readers will try to answer it. It may be a straightforward question, or it may be a trick question. I figure this will give me a better idea of what my readership does and does not understand about what I've written, and give readers a chance to show off their skills.
Challenge #0 happened kind of accidentally in the comment section of this post, and there it was suggested that this might be a cool regular feature. So let's give Challenge #1 a whirl, and see what happens.
The metric of special relativity in Cartesian coordinates, in units where the speed of light 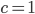 , is
, is
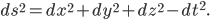
(The d's are just a calculus notation to indicate that you can use this metric to measure infinitesimal distances between nearby points, something which is very useful in general relativity where the metric is a function of position. Here, however the metric is constant in space and time, so you could replace the d's with  's if you like.)
's if you like.)
It has a ten dimensional group of symmetries, called the Poincaré group, which preserve the metric. These are the set of transformations acting on the t, x, y, and z coordinates which preserve the metric. (See the link for details.)
Suppose that instead we want to do nonrelativistic Newtonian mechanics. These are the laws of physics which people believed were true before St. Maxwell and Einstein came along, and which are still valid for describing objects travelling much slower than the speed of light.
1. What is the appropriate metric to use when describing the geometry of spacetime in non-relativistic physics?
2. What is the symmetry group of this metric? How many dimensions does it have?
3. Are these the same as the symmetries of Newtonian physics, which this metric is supposed to describe? Why or why not?
The correct answer to these questions reveals something surprising about the way in which relativity is an improvement on nonrelativistic physics.
You need not answer all of these questions, but the answers to one may help confirm that the answers to the others are correct. Experts (e.g. those with graduate education in physics) are requested to wait a while before attempting an answer, in order to give others a chance to respond.

1.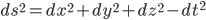
2. Poincare' Group; 10
3. Yes, because there is no Lorentz transformation?
*Not sure if I've properly understood the questions.*
I studied 2 years of fairly basic Physics during an Engineering degree, but I don't have a clue I'm afraid. But I am very interested in your blog, but I enjoy the descriptive rather than the mathematical. Thanks.
Jack,
You've answered questions 1 and 2 for relativistic physics, I was asking about non-relativistic physics, where the speed of light is infinity.
My best guess at 1. is ds² = dx² + dy² + dz²
I don't (yet) know what symmetry groups are.
Dr Wall, I would benefit from this post greatly because my background in not in physics and I was drawn to your blog because I am eager to understand the deep questions of physics and religion. My mathematical background certainly allows me to understand the maths (calculus). So I'll attend all the classes and try to learn as much from you and the participants. Case in point: I now know, for the first time, that the speed of light is infinity in non-relatavistic physics. I always though that the speed of light is 299,792,458 metres per second or about 3.00×10^8, regardless!
Thanks.
TY,
299,792,458 metres per second is pretty close to infinity for all practical purposes. That's why nonrelativistic physics (i.e. Newtonian mechanics) is such a good approximation to the real world! But in fact the speed of light is finite, in other words Newton was WRONG! But not very wrong, most of the time.
Christopher,
That's an excellent guess, and I was hoping somebody would make it. Some good things about your proposal:
1. It treats time and space differently (which makes sense for nonrelativistic physics).
2. It describes the correct geometry (Euclidean space) for space at one moment of time.
But let me ask you these questions:
A. Does it make physical sense to talk about the distance between two points that are at different moments of time?
B. Does it make sense to talk about the duration (i.e. temporal difference) between two points that are at different moments of space?
The mathematical definition of a group is fairly simple, and you can look it up on wikipedia or something if you like. However, you don't actually need to know the definition to answer my question, because it turns out that the collection of symmetries of some object is always a group, automatically. That's why I called it the "group" of symmetries, but maybe I should have just said, what are the symmetries? A description of the symmetries of Minkowski space (i.e. those changes of coordinates which leave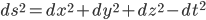 intact) is linked in my post above.
intact) is linked in my post above.
A symmetry is just an operation you can do to a thing that leaves it the same (e.g. if you rotate a square clockwise by 90 degrees, it still looks the same as it did before). If A is a symmetry and B is a symmetry, than doing A and then doing B is always also a symmetry. We can write this as AB, which is not necessarily the same thing as BA (for example, a reflection of the square about an axis doesn't necessarily commmute with a rotation). Secondly, there is a special symmetry which you can always do to any object, corresponding to the operation of "doing nothing". We call this the identity operation and we can write it as I.Finally, you can also undo any operation A--we call this the inverse operation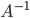 , and it obeys
, and it obeys 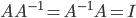 as you might expect. Anything which follows these rules is a group.
as you might expect. Anything which follows these rules is a group.
OK here's my attempt at question 1, based on a possibly mangled understanding of GR:
My guess is that the spatial part of the metric is going to have the same form that Christopher proposed above (in Cartesian coordinates). But since we're considering spacetime, let's incorporate time. The two bits of GR knowledge I used were the Christoffel symbols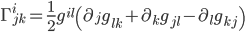 where
where 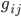 is the ij-th component of the metric and
is the ij-th component of the metric and 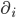 represents partial differentiation with respect to the ith coordinate, and the geodesic equation
represents partial differentiation with respect to the ith coordinate, and the geodesic equation 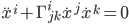 , where
, where 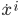 represents differentiation of the ith coordinate
represents differentiation of the ith coordinate 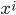 with respect to some parameter (to be identified). You can read about Christoffel symbols here: http://www.wall.org/~aron/blog/the-connection/
with respect to some parameter (to be identified). You can read about Christoffel symbols here: http://www.wall.org/~aron/blog/the-connection/
We're in 4D, so let's say our coordinates are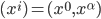 , where
, where 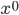 is time and
is time and 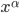 ,
, 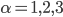 are the x, y, z coordinates. In Newtonian mechanics, the equation of motion of a particle freely falling in a gravitational field is just
are the x, y, z coordinates. In Newtonian mechanics, the equation of motion of a particle freely falling in a gravitational field is just 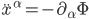 , where
, where 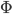 is some gravitational potential, and the dots represent differentiation with respect to time. Given this, we can trivially see
is some gravitational potential, and the dots represent differentiation with respect to time. Given this, we can trivially see 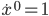 , so we can re-write our equation of motion like so:
, so we can re-write our equation of motion like so: 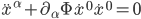 . This looks a lot like our geodesic equation above, with
. This looks a lot like our geodesic equation above, with 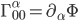 .
.
We can now use our Christoffel symbol formula: , where I've assumed we're working in a basis where the off-diagonal components of the metric are zero. Since
, where I've assumed we're working in a basis where the off-diagonal components of the metric are zero. Since 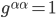 , we have this equation:
, we have this equation: 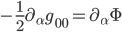 . From this we can easily see that
. From this we can easily see that 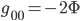 .
.
So for the full metric, I get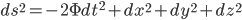 . Unless I've made some stupid mistakes, which is very possible indeed, given that I'm still very new to GR.
. Unless I've made some stupid mistakes, which is very possible indeed, given that I'm still very new to GR.
As for the symmetries, I'm still thinking about that. Will I need to think about Killing fields for that, or is there a more intuitive way of approaching it?
Blessings, Andrew.
Bother and blast, I think I screwed up the Latex on that comment. Sorry...
[I believe I fixed everything---AW]
Andrew2,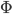 is constant in the absence of gravitational masses, then your metric appears to involve a finite speed of light, while if we take
is constant in the absence of gravitational masses, then your metric appears to involve a finite speed of light, while if we take 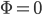 , it reduces to Christopher's answer, which as I hinted above is not quite correct.
, it reduces to Christopher's answer, which as I hinted above is not quite correct.
Nice analysis, and in some ways pretty close to the actual physics of the nonrelativistic limit of GR. It IS possible to formulate the nonrelativistic Newtonian gravity in terms of Christoffel symbols, but there is a catch (which I am not yet ready to reveal). But your final answer for the metric predicts time dilation near massive objects, and that is not a feature of the Newtonian gravitational theory. Also, if we assume that
Also, I originally intended the challenge to be to describe the metric of classical Newtonian mechanics without worrying about gravity. So the answer I was looking for is simpler than what you wrote down.
This is a cool idea. But can I ask, is the 'd' in the metric for GR, just like delta or 'change in'
Sorry I couldn't answer your Qs, I'm a bit of a physics-noob :/
Thanks for the feedback and criticism - very much appreciated. I was a little concerned as to why my answer didn't quite look like the non-relativistic limit of GR, but it occurred to me that you generally get that by considering perturbations around the Minkowski metric, and there didn't seem a way to justify that from a pre-Einstein perspective (I'm guessing that's not the right answer anyway, so it's a moot point). I look forward to you revealing the catch with using Christoffel symbols. It didn't occur to me that time dilation would be an issue, but now you point it out it is obvious. I'm not sure I understand why a constant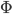 without gravitational masses implies a finite speed of light - could you explain?
without gravitational masses implies a finite speed of light - could you explain?
My bad about the gravity - didn't realise we could ignore it. I shall have another ponder about the problem - it's quite interesting.
charlie, signifies that it's an infinitesimal change in the quantity. It's the same type of "d" that comes into the expression for derivatives, like
signifies that it's an infinitesimal change in the quantity. It's the same type of "d" that comes into the expression for derivatives, like 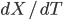 .
.
Yeah, the "d" means the change in the quantity. The fact that it's a lower case d instead of
By the way, when we write something like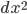 , it always means
, it always means 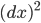 and not
and not 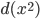 . Both sides of the expression for the metric involve an infinitesimal expression squared, so they match.
. Both sides of the expression for the metric involve an infinitesimal expression squared, so they match.
Andrew2,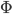 may be taken to be constant. Suppose for example that
may be taken to be constant. Suppose for example that 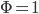 . Then your metric is just the Minkowski metric, which has a finite speed of light.
. Then your metric is just the Minkowski metric, which has a finite speed of light.
If there's no masses, then the gravitational potential
42?
Hey Dr. Wall
Sorry for not commenting in such a long time, I've been taking summer courses to finish my degree. I'd like to make a suggestion concerning this post. I think it would greatly appreciated by all of your followers if you had a terminology page that would help they lay persons such as myself understand these technical posts a little better. If there is one then my apologies. I also had a question. What book/books would you recommend for your followers to help catch us up with the technical side of your work.
Thanks for your work. God Bless!
Sadly, the truth must now be known (as if you didn’t know it already), I’m completely out of your league, Aron. I do understand the scientific statements you and some of the others make (most of the time) but not much of the math. So with i like pizza, I have to say the answer is 49. (Please watch the Hitchhiker’s Guide to the Galaxy again. I’m pretty sure that the answer was not 42.)
Also, along with John-Michael’s suggestion, may I ask that you consider giving a layperson’s summary after you’ve made a technical scientific statement? You do usually do this, but of course, because of people like myself, I want to remind you.
John-Michael and Dennis, you shouldn't be so hard on yourselves! :-) You might be surprised at how well you can do with what's been given so far, even without a lot of math.
The problem starts with the metric of special relativity and asks for one that would describe the kind of universe Newton's laws take place in. Note that as Aron pointed out, Christopher already has part of a working answer. Compare his metric to the one given for special relativity. How is it different? What needs to be added to make it similar to the relativistic one but descriptive of the kind of universe assumed by Newton's equations? How would you change coordinates in it without changing the way those equations work? See where this leads you, and I bet you'll do better than you think!
1.
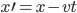
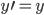

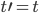
2. Lorentz group; 10
3. No, this is the Galilean group.
Please feel free to edit my LaTeX for (1).
[Done! Regrettably, \eqalign{} and other array commands don't seem to work on my setup. Also, although > and < are dangerous due to their use in html tags, you don't have to worry about = causing problems--AW]
Also, I meant to say that the second part of (2) is 6.
Man, I messed that all up! I got confused by some of the comments. Let me try one last time: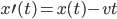 .
.
1. Suppressing two spatial dimensions, we have
2. Galilean group; 10
3. Yes, because it assumes absolute space and absolute simultaneity.
I think (1) is a Euclidean metric d(x,y) = sqrt of (X1-Y1) + (X2-Y2) . . . + (Xn - Yn) end sqrt
I think the Euclidean group works for Euclidean space of n dimensions.
[you can type \sqrt{(X1-Y1) + (X2-Y2) . . . + (Xn - Yn)} inside two pairs of dollar signs, you know, and it will look like this:
--AW]
Jack,
You have correctly stated the symmetry group of nonrelativistic physics, which is (part of) question #3! (Since you didn't write down a metric, questions #1 and #2 are still unanswered...) The symmetries of Newtonian physics are indeed given by the Galilei group! This is credited to St. Galileo because he was the first to observe (so far as I know) that the laws of physics don't care what velocity you are travelling at. They are the same in every reference frame.
(We usually think about Einstein in this context, but he didn't invent this "Principle of Relativity"! Instead, he showed how to modify it to make it consistent with St. Maxwell's equations, where light always travels at a constant speed.)
If we switch to the frame of reference of an observer travelling in the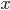 direction at velocity
direction at velocity 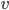 , then the formula for the boost in the
, then the formula for the boost in the 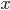 direction is what you wrote down:
direction is what you wrote down:
The Galilei group is the group of symmetry transformations you get by combining the space/time translations, spatial rotations, and a "Galilean boost" aka a change of velocity. It has 10 dimensions, just like the Poincare group. (Or you can leave off the 4 translations, and just consider symmetries which hold fixed a given point. Then it has 6 dimensions, just like the Lorentz group (the corresponding entity in Special Relativity.)
David,
That is indeed (one way of writing) the metric of an n-dimensional Euclidean space, but what are you going to do about time?
Christopher (or anyone else),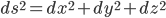 . What happens if I take your metric and do the substitution suggested by the Galilei boost? Is this formula the same in this new reference frame (i.e. as seen by a moving observer?)
. What happens if I take your metric and do the substitution suggested by the Galilei boost? Is this formula the same in this new reference frame (i.e. as seen by a moving observer?)
You suggested the metric
Scott,
Thanks for raising the morale! You didn't mention that, although the amateur commentariat is well on its way to solving my problem, there is a counterintuitive twist which I thought would throw off even the experts for a moment... so nobody is to succumb to either presumption or despair!
1. If my understanding of non-relativistic classical mechanics is correct, then there is no metric describing an invariant spacetime interval: time is treated as universal with a constant rate of passage that is independent of the state of motion of an observer; the Galilean transformation leaves the time coordinate unchanged and only changes the space coordinates. Moreover, there exists an absolute global time function that foliates spacetime by the same simultaneity planes for all inertial observers. In other words, a Galilean transformation can change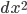 between two given events, but always leaves
between two given events, but always leaves 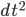 unchanged.
unchanged.
If we are talking solely about a spatial metric, then it seems to me that the use of Euclidean space is appropriate: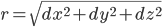 .
.
2. Galilean group; 10
3. Yes, because Newtonian physics posits an absolute global time that does not depend on reference frame.
Oh, sorry Aron, I am trying to learn LaTeX, but all I can say is Newton had an independent global time, but I can see there are a few people here who are smarter than I am, so I think I'll leave it to them
Jack,
OK, that's pretty much correct. I'm going to declare you the winner, and give the answer key for the questions.
[SPOILERS FOLLOW:]
1. When I was describing special relativity above, I set the speed of light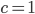 to be tricky. If you restore the powers of
to be tricky. If you restore the powers of  in the metric, you get either
in the metric, you get either
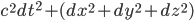
or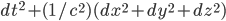
depending on whether you scale the metric to measure distances, or times. Taking the limit of the latter expression asAnother way to get the same answer: It's already been mentioned that Newtonian mechanics is invariant under the Galilei group. This means that in particular:
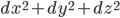
is not symmetric the transformationInstead, up to an overall constant multiplying it out front,
2. While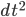 is preserved under all the symmetries of mechanics, it has a lot MORE symmetries then we wanted it to. In fact, at any time it is symmetric under ANY transformation of the space coordinates x, y, z, even something horrible like
is preserved under all the symmetries of mechanics, it has a lot MORE symmetries then we wanted it to. In fact, at any time it is symmetric under ANY transformation of the space coordinates x, y, z, even something horrible like 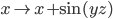 . This is an infinite dimensional symmetry group, not at all the same as the Galilei group which is 10 dimensional.
. This is an infinite dimensional symmetry group, not at all the same as the Galilei group which is 10 dimensional.
3. The moral of the story is that you need additional structure, besides the metric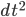 , to describe the physics.
, to describe the physics.
In fact, Newtonian mechanics involves all of the following structures:
a) a global time foliation into slices of constant time "t",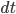 (which may be squared to obtain the time-metric
(which may be squared to obtain the time-metric 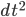 )
)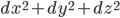 which is valid only for comparing events at the same time
which is valid only for comparing events at the same time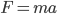 , one also needs the Christoffel symbol
, one also needs the Christoffel symbol 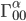 .
.
b) a measure of time passing
c) a spatial metric
and
d) in order to define acceleration in
All of these structures (a-d) are implicit in a Galilean spacetime. This is in sharp contrast to Special or General Relativity, where everything you need comes from the metric.
And thus, the moral of the story is... Relativity is a LOT SIMPLER than nonrelativistic mechanics. Who woulda thunk?
Andrew2,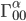 is actually not determined by the choice of metric. (The usual formula
is actually not determined by the choice of metric. (The usual formula
I now reveal the secrets which I promised you earlier. As I said above, in nonrelativistic mechanics the Christoffel symbol
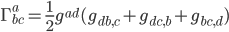
is ill-defined, because the inverse metricHence, you have to think of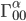 as a field which is independent of the time or space metrics. If this field is allowed to vary, it behaves just like a gravitational field, and in Newtonian gravity it comes from a potential which is sourced by the masses via the Poisson equation. Basically what you wrote down, but where
as a field which is independent of the time or space metrics. If this field is allowed to vary, it behaves just like a gravitational field, and in Newtonian gravity it comes from a potential which is sourced by the masses via the Poisson equation. Basically what you wrote down, but where 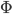 isn't viewed as the time component of the metric. This is a formulation of Newtonian gravity in which Einstein's Equivalence Principle is manifest.
isn't viewed as the time component of the metric. This is a formulation of Newtonian gravity in which Einstein's Equivalence Principle is manifest.
Dennis, the answer to life the universe and everything is indeed 42. While reading this thread I used the Google translator, only to find out that this was already in English! Believe it or not I enjoy eavesdropping on geniuses. I can't begin the understand the question but I hope you continue this.
That does it, Andy and i like pizza, I've got to watch Hitchhiker's Guide again. How could I confuse 49 with 42? This was one of the most important discoveries in the history of the universe.
Hey Dennis, don't worry... I have no doubt that somewhere out there in the "multiverse" there's a bubble universe where the answer is 49! :D
Scott,
That is awesome!!!
Thanks Jack! It came to me out of nowhere while I was lying drunk in a field near Innsbruck. [Just kidding... :-)]
Hey Aron, this was great! I was thinking about this question, and found your website/blog as a result. It wasn't obvious to me that it was impossible, so I actually tried to solve for this "Galilean metric tensor" under the "standard" assumption made for special relativity,
Where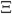 was the matrix corresponding to the general Galilean transformation. Upon working it out, you find a possible source of degeneracy in the leniency of the top-left element (corresponding with
was the matrix corresponding to the general Galilean transformation. Upon working it out, you find a possible source of degeneracy in the leniency of the top-left element (corresponding with 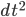 ), and even if you remove the possible degeneracy in that element, the remaining equations prove to be unsolvable (unless the other diagonal elements are zero).
), and even if you remove the possible degeneracy in that element, the remaining equations prove to be unsolvable (unless the other diagonal elements are zero).