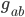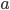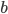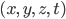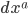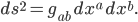Today I went to a talk by Lawrence Krauss entitled “A Universe from Nothing”, which had the following abstract:
The question, "Why is there something rather than nothing?" has been asked for millenia by people who speculate on the need for a creator of our Universe. Today, exciting scientific advances provide new insight into this cosmological mystery: Not only can something arise from nothing, something will always arise from nothing. Lawrence Krauss will present a mind-bending trip back to the beginning of the beginning and the end of the end, reviewing the remarkable developments in cosmology and particle physics over the past 20 years that have revolutionized our picture of the origin of the universe, and of its future, and which have literally revolutionized our understanding of both nothing, and something. In the process, it has become clear that not only can our universe naturally arise from nothing, without supernatural shenanigans, but that it probably did.
In the first 45 minutes, he provided an animated and reasonably clear explanation of concordance cosmology, the current version of the Big Bang model, dating from the discovery in 1998 that the expansion of the universe is accelerating (rather than decelerating as one would expect from the attractive gravity of ordinary matter). This is exciting but now well-established work, which I've heard about a hundred times before, but was probably new to many of the people in the audience. It was peppered with occasional off-hand sneers at Republicans, Theology, and Young Earth Creationism, but for the most part it was a pretty valiant stab at popularizing an important set of 20th century discoveries.
The real reason I was there, of course, was to listen to his claims in the last 15 minutes that modern cosmology somehow points to the nonexistence of a Creator. His claim was that there is evidence that the universe came from "Nothing" according to physical processes, and this apparently is supposed to undermine the religious view that God created the world supernaturally. There were so many things wrong with this part of his talk, both a physics and a philosophical perspective, that I'm not entirely sure where to begin. But let's try anyway.
His Slam on Theology. Krauss said that Theology wasn't based on empirical evidence, so therefore he didn't believe it. That was it. He didn't seem to take any particular theological ideas seriously enough to even try to define them, let alone refute them. There was no indication that Religion had any other origin besides a bunch of clueless dudes sitting around asking "Why is there Something rather than Nothing?" (In the case of Christianity, I thought it had more to do with a guy claiming to be God, doing miracles, and dozens of people saying that they saw him alive after he was killed. But what do I know?)
But let's get back to cosmology, since that was the subject of his talk. It used to be that Christians believed that the world was created a finite time ago, out of Nothing. Although some of them, like St. Thomas Aquinas, said that God could have created a universe with an infinitely long past. Atheists had (and have) a diversity of opinions, but most of them thought that things would make more sense if the universe were around forever, since then maybe you wouldn't have to explain where it came from. Then Big Bang cosmology came along, and it now seems—provisionally speaking—like the Universe really did have a beginning. Now some atheists think they can refute the Christian view that God created the Universe from Nothing by arguing that the world did emerge from Nothing. The role-reversal here is a little strange.
What Christians mean by creation ex nihilo is that God created the Universe, but that he didn't make it out of any pre-existing stuff that was lying around. Thus, while the universe didn't come "out of" anything, it still comes from God.
What Krauss seems to mean is something quite different, namely that there's some specific entity we can talk about called "Nothing", which has suitable properties for generating our universe.
But the universe can only come from nothing if you define a certain kind of something as being "Nothing". Duh, because any explanation by its very nature must explain one thing in terms of some other thing! This other thing must be taken for granted for purposes of the explanation. Now, Krauss actually referred to 3 different ideas which he called "Nothing #1, #2, and #3":
Nothing #1: an "empty" spacetime a.k.a. the vacuum. In ordinary non-speculative quantum field theory (QFT), the "vacuum state" (the configuration of fields with the lowest energy) is actually filled with so-called virtual particles which can affect physics in various ways. At least, that's what the popularized physics books say; if one actually studies quantum field theory rigorously, people tend to use somewhat different language since the notion of "virtual particle" can be difficult to define. But let's spot him the terminology since he was talking to a popular audience.
Krauss claimed that if you start with an empty space which has no virtual particles in it, virtual particles will appear, and this is "something" coming from "nothing". This is bosh, since strictly speaking, there's no such thing in QFT as a state with no virtual particles. (If there were, it would be infinitely different from the vacuum state, and would therefore have an infinitely large energy. That's not nothing at all!) If anything can colloquially be called "Nothing" in QFT, it is the vacuum state. But this state already has all those virtual particles in it. And as time passes, this vacuum evolves to....wait for it....itself! That's right, if you agree to call the vacuum state Nothing, then Nothing comes out of it. (He seemed to think this story might change once you take gravity into account, due to negative energies, but I didn't really understand this suggestion so I won't comment on it.)
The QFT vacuum isn't nothing. Of course, from a strict philosophical point of view, the vacuum state of QFT is not Nothing since it's filled with all those virtual particles, and even aside from that, there's the space and time geometry, which is not Nothing. To fix this he started taking up a different kind of nothing:
Nothing #2: the absence of any space or time. This actually connects to an interesting quantum gravity idea known as the "Hartle-Hawking state" or the "no-boundary boundary condition". (Jim Hartle is on my floor at UCSB, by the way.) The suggestion is that the laws of physics not only tell you how the universe at one time evolves to a later time, they also tell you what the initial state of the universe is.
In some sense, one can think of this state as emerging out of Nothing #2. However, the sense in which this is true is subtle. There's another sense in which the Hartle-Hawking state does not emerge from Nothing; rather it has existed for an infinite amount of time— the popular physics articles never mention this, for some reason! This is an interesting and important idea, but I think it deserves to be in it's own post, after I've explained QFT better. The important thing to know is the following:
The crucial physics here is totally speculative! It was entirely based on speculative ideas about quantum gravity which anyone working in the field would admit are not proven. This is because we currently have no experimentally testable theory of quantum gravity! (Nor do we even know how to formulate a consistent theory of quantum gravity mathematically, except perhaps in some special situations that probably don't apply to the beginning of our universe)
I mentioned this in the Q&A afterwards. My comment seemed to aggravate him a little, since he thought he'd been sufficiently clear about this. But I discovered that at least one member of the audience was still unclear on which parts were speculative, and which weren't, at the end of the lecture. In my experience, one has to be crystal clear about this sort of thing when speaking to a popular audience, or they tend to walk away thinking that "Science" has proven things when it hasn't.
Atheists such as Krauss scorn theology as being completely non-empirical. They claim it is not based on evidence of any sort. I find it extremely ironic when this sort of atheist thinks that speculative quantum gravity ideas are just the right thing to further bolster their atheism. Suppose you think that Science is better than Religion because it is based on evidence, and suppose you also want to refute Religion by using Science. Here's a little hint: consistency would suggest using a branch of Science that actually has some experimental data!
The universe has zero energy. Krauss thinks that the universe coming out of Nothing has been made more plausible by cosmology. To understand his terminology, you have to know that (roughly speaking) a closed universe means that space at one time is finite in volume, and shaped kind of like a sphere, so that if you travel around the universe far enough you come back to where you started. On the other hand, in a flat universe, space at one moment of time is shaped like ordinary Euclidean geometry, and is infinitely large. Current observations indicate that the universe is flat. As far as I could tell, Krauss' argument can be translated into these terms:
- The total energy of a closed universe is zero. (It's tricky to define energy in general relativity, but according to one commonly used definition, this is true.)
- Conservation of energy suggests that if the universe came from Nothing, it should have zero energy.
- If there was a period of extremely rapid expansion at the beginning of the universe (as evidence suggests there was—this is called inflation), then whether or not the universe started out closed, it should look flat today.
- But the universe does look flat,
- Therefore Science suggests that the universe was created out of Nothing,
- Therefore there is no need for God.
Perhaps I'm missing some crucial steps in his argument. But there seem to be several enormous leaps of logic in there.
The Hartle-Hawking state isn't Nothing either. Strictly speaking, even the Hartle-Hawking idea doesn't strictly get the universe out of Nothing, since it says that the initial state of the universe depends on the laws of physics. Now the laws of physics aren't nothing. So if, for example, you are wondering if there is any role left for the Creator, then one might say he picked the laws of nature.
Now, there's all sorts of difficult philosophical issues involved in what's called the Cosmological Argument for the existence of God. But it's hard to get into them with someone like Krauss who is so dismissive of Philosophy. The trouble with people like that is that it isn't possible to just find things out using Science instead of Philosophy. That's because you have to do Philosophy to know what is or is not implied by Science. People who dismiss Philosophy still end up doing it; they just do it badly, without a critical examination of their premises.
Nothing #3: the string theory multiverse. Krauss acknowledges that the laws of phyiscs themselves might seem to call for an explanation. Especially since the various constants of Nature seem to be "fine-tuned" to allow the existence of life (I'll go into this in much more depth later). On the face of it, this seems to be at least some mild evidence for the existence of God, but Krauss would never admit such a thing.
He suggests that we can explain this fine-tuning if string theory turns out to be true. That's because string theory has an enormous number of different possible configurations, that look like universes with different laws of physics. Some people have suggested that if there's a gazillion different universes (known as the "multiverse"), each with its own laws of physics, that it's not surprising that one of those universes should support life. Krauss admitted that there was some dispute as to whether this idea counts as "Science", what with it being totally speculative and arguably untestable. But what I want to know is, why the $@#& would we ever refer to an infinite number of universes, governed by the principles of string theory, as a Nothing?
I should say that this review is based entirely on Krauss' talk. I have not read his book, but I have read this negative review by philosopher St. Feser.
[Update 7/21/20: added two paragraphs to the text, beginning "What Christians mean..." to make the argument a little clearer.]
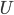 ) is optimum: the best possible.
) is optimum: the best possible.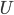 here aren't exactly the same as the "possible worlds" discussed by analytic philosophers. If the best possible kind of universe contains something like free will or nondeterminism, there will be multiple "possible worlds"
here aren't exactly the same as the "possible worlds" discussed by analytic philosophers. If the best possible kind of universe contains something like free will or nondeterminism, there will be multiple "possible worlds" 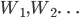 consistent with the same overall plan
consistent with the same overall plan 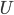 of the universe, some of which may be morally better or worse compared to the others.]
of the universe, some of which may be morally better or worse compared to the others.]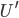 as best. It seems infinitely unlikely that
as best. It seems infinitely unlikely that 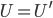 just by coincidence, so it seems to be almost certain that the universe will appear to us to contain evils that we can't explain. One can argue about whether this is a sufficient explanation, but it's definitely something that has to be taken into account. The idea that a superhuman entity which created the universe will see things exactly the way we do is absurd:
just by coincidence, so it seems to be almost certain that the universe will appear to us to contain evils that we can't explain. One can argue about whether this is a sufficient explanation, but it's definitely something that has to be taken into account. The idea that a superhuman entity which created the universe will see things exactly the way we do is absurd:
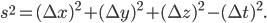
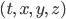
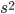
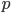
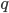
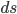
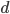
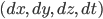
![(ds)^2 = g_{xx}\,(dx)^2 + g_{yy}\,(dy)^2 + g_{zz}\,(dz)^2 + g_{tt} \,(dt)^2 + \\ 2[ g_{xy}\,dx\,dy + g_{xz}\,dx\,dz + g_{xt}\,dx\,dt + g_{yz}\,dy\,dz + g_{yt}\,dy\,dt + g_{zt}\,dz\,dt].](http://www.wall.org/~aron/blog/wp-content/plugins/latex/cache/tex_db669a03022d92c818e3bbe67f915b2f.gif)