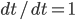Flesh and Spirit I: Creation

by Aron Wall Posted on March 23, 2015

"What is born of the flesh is flesh, and what is born of the spirit is spirit." — Jesus

I want to talk about something which is essential to the Gospel, yet widely misunderstood.  It has to do with the relationship between our flesh and our spirit.

Clearly we have both of these things.  We know we have a physical body, and we know we have something like a mind or inner self, with a personality, consciousness, and also deep subconscious mysteries that we do not fully understand.  Our mind has to deal with various urges and desires which come up from the physical or animal side of our nature, but we also have a sense of ourselves as rational and spiritual beings.  We have both a body and a soul.

I think this is all obviously true no matter what we decide about the philosophy of mind.  Leave aside the metaphysical questions, I think we know that all of this is true from our experiences as human beings (if I wanted to be fancy I would use the word phenomenology here).  Materialists assert that the mind is just another name for certain arrangements of matter, specifically the neural network in our brains.  For the purposes of what I have to say, my response is who cares?  That doesn't change the fact that we experience ourselves as having a more physical and a more mental part.

Suppose you fall to the ground upon hearing some devastating news, and a sympathetic materialist philsopher walks by.  "Are you okay," he says?  "My body feels fine," you say, "but my heart is broken."  Somehow he knows what you mean.  There is no need for him to reply: "Technically, your mind is part of your body, and oh by the way you should have said brain instead of heart.  We now know that the heart pumps blood, it doesn't think."

Also, when I say we have both flesh and spirit, I don't necessarily mean that they can be separated in a clean way.  Our physical condition affects our mind, which in turn controls our body.  Our bodily desires cannot be experienced until they enter our mind.  There's not necessarily a clear-cut distinction between where one ends and the other begins.  But even if it's a continuous spectrum, we can still label the two ends of the spectrum, and decide how we feel about each of the two ends.

So what should we think about our physical or fleshly self?  This is a key distinction between Christianity and several heretical off-shoots such as Gnosticism or Manicheeism.  These sects taught that the physical world was evil, and that human beings are basically souls trapped in bodies.  Matter is evil, spirit is good.  Many Gnostics even claimed that the creator of the physical world was a lesser, evil god several emenations removed from the true God.  If this is true, then salvation consists of being rescued from our physical or corporeal nature.

But Christianity could not disagree more.  Matter as such is not evil, nor is it morally neutral, it is fundamentally good!  We believe that the physical universe is intrinsically good and glorious because it reflects the infinite splendour of the one who created it.  Seven times he calls it good; three times he blesses it:

God saw that the light was good...

God called the dry ground “land,” and the gathered waters he called “seas.” And God saw that it was good...

The land produced vegetation: plants bearing seed according to their kinds and trees bearing fruit with seed in it according to their kinds. And God saw that it was good...

God made two great lights—the greater light to govern the day and the lesser light to govern the night.  He also made the stars... And God saw that it was good...

So God created the great creatures of the sea and every living thing with which the water teems and that moves about in it, according to their kinds, and every winged bird according to its kind. And God saw that it was good.  He blessed them and said, “Be fruitful and increase in number and fill the water in the seas, and let the birds increase on the earth.”...

God made the wild animals according to their kinds, the livestock according to their kinds, and all the creatures that move along the ground according to their kinds. And God saw that it was good...

Then God said, “Let us make mankind in our image, in our likeness, so that they may rule over the fish in the sea and the birds in the sky, over the livestock and all the wild animals,and over all the creatures that move along the ground.”
___So God created Man in his own image,
___in the image of God he created him;
___male and female he created them.
God blessed them and said to them, “Be fruitful and increase in number; fill the earth and subdue it.”...

God saw all that he had made, and it was very good...

Then God blessed the seventh day and made it holy, because on it he rested from all the work of creating that he had done.

If this were not enough, we also know that the Word of God became flesh, that he physically rose from the dead, he communicates his flesh and blood to us through a physical sacrament, and that on the Last Day he will raise all of our bodies from the dead.  The Incarnation and the Resurrection show that God of the New Testament is the same as the God of the Old Testament: he continues to bless the physical, corporeal, material world.

The implications of this for our self-conception could not be greater.  It means that we must resist as a damnable heresy the idea that we are souls trapped in bodies.  We are meant to be physical.  We must treat our bodies with respect and strive for integration between our souls and our bodies.  They are part of who we are.  If we think of ourselves only as "souls", we will be continually frustrated by our inability to live up to our own prideful perfect image.

Most people struggle with shame, and with various body image problems.  The first step is to recognize that our body is indeed created good by God—I'm not saying that a merely intellectual affirmation is a magic bullet, but it's a start.  Instead of restricting our sense of identity to the smallest that it can be, a speck of consciousness in our skull, we must extend it to the extremities of our body.  Even our spouse's body if we are married.  (Note that all Christians are married to Christ, whose physical body in turn includes all of us in the Church, whether on Earth or in Heaven).

With respect to human faculties, we must accept the rule that every constitutent part of human nature is good.  We cannot identify any part of ourselves, e.g. our capactity for anger or sex, or our ability to rule over Nature, and say that this is evil.  It was created good by God.  We may corrupt or twist it by sin, or it may be stunted by disease or deformity, but the original plan and purpose was good.  Even if our anger leads us astray 99% of the time, we cannot say that anger, depression, anxiety, pain, pleasure, or joy are inherently bad.  Jesus experienced all of these feelings.  Admittedly he chose to remain celibate for the sake of the Kingdom of God, but Genesis 1-2 makes it clear that God blesses sex and fertility.

And yes, this includes gender.  God created us male and female, each one in the image of God (who, you will notice, speaks of himself in the plural at this point).  Although our salvation in Christ does not depend in any way on gender, the details of our personality are influenced in countless ways by our particular makeup, and our gender will remain eternally part of who we are.  This is good.  Of course, the things which humans have in common are more important than the things which separate us.  But we cannot give up on entirely on gender distinctions (like some Gnostics tried to do) simply because people have often used them to oppress people.  If gender roles seem oppressive, that is because they have become distorted by sin, not because they are inherently bad.  Men, embrace your masculinity!  Women, embrace your femininity!  (I don't mean the sterotypes or false generalizations, but the truth of who you really are.)

Our spirtual self is also obviously good and noble, even if sometimes it seems to be more trouble even than our corporeal self.  Still, it is what makes us human.  Even if we attempt to live as if we were merely animals meant for pleasure, we will never succeed.  I don't just mean that it can't lead to satisfaction (as the book of Ecclesiastes points out) but also that people can't help but turn even simple ethical nihilism into some sort of weird affected ethical game.  We are human beings, we can't help it.  As the Bl. Simone Weil said, "Man would like to be an egoist and cannot.  This is the most striking characteristic of his wretchedness and the source of his greatness."

So if we were created good, then why are we all so royally fucked up?  (Pardon my French, but I cannot think of an equally potent and apt word to describe the human condition.)  That will be the subject of the next post in this series.

But let me just say now that for a long time the Church has over-empasized the faults of the physical world, and embraced a severely ascetic mindset.  This was wrong, as it implicitly denied (what was theoretically admitted as doctrine) that the world was created very good.  But we are now so hedonistic as a culture, even in the Church, that we are not likely to make the same mistake.  In the present day we are much more likely to fail to see the need to crucify the flesh with its desires and passions!  (Gal. 5:24) Seems like a total contradiction with what I said before, doesn't it?  But without this you cannot be saved, so it's a bit of a shame no one talks about it much these days, because it is an essential part of the Gospel which has the power to save you.  More on this to come.

Next in series: Flesh and Spirit II: Original Sin

Posted in Theology | 8 Comments

Against Pantheism

by Aron Wall Posted on March 12, 2015

In the comment mines I suggested, off-handedly, three possible metaphysical explanations for consciousness, without endorsing any of them.

A reader John responds to one of these suggestions:

To my primitive mind, this seems to be the most valid argument:

3. In fact, it is not possible to explain consciousness from nonconscious entities. Therefore, the most fundamental thing in existence is a mind, and we are parts of that mind. Matter is just a delusion which this mind believes in for some unknown reason. (I don't find this view plausible at all, but that's not the point.)

This is a longstanding view from oriental philosophy, and it intrigues me why you don't find it plausible.

Thanks for your comment.  My main reason for finding this type of Pantheistic/Idealistic view implausible are these:

1. Matter sure seems like something with a real, consistent, and objective nature, quite unlike a dream.  For example, when I wake up my furniture and stuff is always in more or less the same place.  There are trees by the road whether or not I care for them to be there.  As a physicist I can make precise models of how matter will behave under certain circumstances, and in fact it does those things.  It does not consult my wishes except when I act on it using my body, and even then things do not always go according to plan.

Matter is a very parsimonious explanation of practically every experience I have.  So considering it a delusion seems unjustified.  And even if matter were a illusion, it must still exist as an illusion; if I hallucinate a blue tiger, there may not be a real tiger in the room but there is still a real image in my mind.  So saying matter is an illusion doesn't actually reduce the number of entities which need to be explained!  Actually it makes things worse, because I cannot think of any reason why God would have the type of schizophrenia required to think he is multiple persons living in a common environment.  Nor can in turn be an illusion that I suffer from illusions, since that would be a logical contradiction.

(Speaking very broadly—since there are many varieties of Hinduism and Buddhism—a lot of these oriental philosophies don't really believe in logic in the first place, or only use it to argue for contradictions, so that we give up our dualistic forms of logic.  But I could never accept that perspective on logic in a million years---there is literally nothing more illogical than denying the validity of logic!  I refuse to be insane.)

2. If we define God as the ultimate explanation for the Universe, which cannot itself be explained, then to say that everything is God is to say that nothing at all can be explained.  But if a view explains nothing, it is less good than a view which explains, well, anything!  I touched on this point in my discussion of Pantheism in my series on Fundamental Reality.

3. The actual Creator of the universe has spoken to me both in the Bible and in personal conversation, and he does not seem to regard other people as as part of himself in the requisite fashion.  To Moses, he says "I am who I am" (Exodus 3:16), not "I am who you are".  In fact he seems to disapprove of a number of specific things which human beings do—we Christians call these things "sin".  And as I have argued, if God is good and we are not, then it follows that we are not God.  To think that we are parts of God might be gratifying to our pride, but it is more wholesome to realize we are not God, and instead accept that we are created beings loved by him.  As St. Chesterton said:

I want to love my neighbour not because he is I, but precisely because he is not I.  I want to adore the world, not as one likes a looking-glass, because it is one's self, but as one loves a woman, because she is entirely different.  If souls are separate love is possible.  If souls are united love is obviously impossible.  A man may be said loosely to love himself, but he can hardly fall in love with himself, or, if he does, it must be a monotonous courtship.  If the world is full of real selves, they can be really unselfish selves. (Orthodoxy, "The Romance of Orthodoxy")

Only in the case of one human being did God identify himself so fully with him, as to allow him to share completely in his divine titles and identity.  And Jesus was no ordinary human, what with being the Word of God, who pre-existed with him from the beginning!  If we were divine beings, we would know it.

True, by receiving the gift of Jesus's Spirit, we do become by grace "partakers of the divine nature" (2 Peter 1:4).  But this is not the same as being the unique and uncreated Son of God.  To be commune with God is not the same as to be God.

So it's important for the distinction between the Creator and created to be sharply distinguished from the beginning.  Once that's 100% clear, we can allow the mystics the liberty to speak the "language of love" concerning the intimate union between themselves and God, without fear of being misunderstood.  I could say to my wife that I am part of her and she is part of me, without either of us thinking that we must be the same person in a literal sense.

Posted in Metaphysics, Theology | 46 Comments

For the Love of God!

by Aron Wall Posted on March 11, 2015

A reader who goes by the name of Petronius Jablonski—I suppose I should call him St. Petronius—has been vigorously arguing against Free Will in the comments to my recent post about Special Relativity, beginning with this comment:

Thanks for the lucid sketch of A Theory & B Theory. You have a knack for writing about philosophical head-scratchers in plain English. I envy your students. (Consider something book-length. A Christian physicist should have no trouble finding an agent.)

We should add free will to the list of controversies in Theology where there is decisive evidence coming from Physics. Isn't the B Theory a stunning depiction of Divine Determinism? God creates this massive, amber-like slab of past, present, & future, all parts of which are equally “real.” How could any single detail have been otherwise unless God made it differently?

Far from being incompatible with Christian theology, this takes St. Paul at his word: Why does God hold us accountable and punish us if we have no free will? This is what Romans 9:19 is asking. St. Paul puts the question into the mouth of an imaginary disputant after stating that God has mercy on some (Moses and Jacob) and hardens others (Esau and Pharoah). His answer does not mention free will, middle knowledge, or allowing evil in the best possible world. The answer is the single most terrifying thing in any of the world's religions: Who are you to ask? God creates some men to be vessels of wrath, others to be vessels of mercy. The purpose is to demonstrate His power. Reality is not about us or our standards. We have no inalienable right to free will (only the Prime Mover has that). God, like a potter making different vessels for different reasons, has the absolute right to make whatever He wants for whatever reason He wants. (Ouch! This is so harsh, but there you have it.) https://www.biblegateway.com/verse/en/Romans%209:19

Note the explicit denial that moral responsibility requires the capacity to do otherwise. "Why does He still find fault? Who can resist His will?" = It's not fair that God judges us because we couldn't do otherwise! St. Paul's answer chills the blood. Damnation isn't about people abusing their free will; it's how God shows His power and mercy to the Elect (in the same way He demonstrated His power by hardening Pharoah's heart and then destroying him). Again, ouch, but that's what it says. For some, the appeal of Christianity is that it takes determinism seriously.

I await your book on physics & the B theory of time supporting the plain teaching of Romans 9. This would be a bestseller. ;o)

Thanks for your pre-order of a book I haven't agreed to write, but I don't think it will say what you hope it will say...

You're mistaken that the B-theory implies Determinism.  From the statement:

(1) The past, present, and future are all equally real,

it is simply not possible to derive the statement

(2) Nothing could have been otherwise,

by any logical argument, not without smuggling in premises that are far more substantive than (1) is.

Most of these premises, ironically, involve smuggling in A-theoretic presuppositions about the nature of the past.  An A-theorist might believe that "The past is unchangeable, but the future is still open", but B-theorist can hardly uncritically accept either statement as it stands.  Why should we adopt the first statement and not the second?  Instead let us say that all time is as contingent as the future, as real as the present, and as definite as the past.

Your "massive, amber-like slab" is more poetic metaphor than physics.  If we want to go by what Physics says, we have to take into account Quantum Mechanics as well as Relativity, and this seems to indicate that if we turned the clock back and re-did the experiment, so to speak, we would not get the same outcome a second time.  Physics can only make probabilistic predictions.  I claim that, having the exact same motivations and neural structures at 12:00 pm, and fixing my perceptual experiences after that, there are still multiple possible things I might decide to do at 12:01 pm.  There is no infinite regress, unless we assume that what I choose to do at an instant must be determined by who I am at that instant.

Also, if it were true that the B-theory conflicts with Free Will, then this would imply that God also has no Free Will, since he himself exists eternally.  Thus your claim that the B-theory supports Calvinism is self-contradictory.  Similarly for arguments based on a supposed infinite regress.  These arguments against Free Will could also be applied to God, if they were really valid.

Now onto your theological claims.  I notice that in your various comments you only cite the Scriptures that support your claims, while ignoring those scriptures that might tell against you (e.g. Romans 11 a couple of chapters later).  Romans 9 is indeed in the Bible (as are the other verses you cite in a later comment I didn't quote) but you have misunderstood it entirely.  It's funny how Calvinists take St. Paul's series of rhetorical questions as if they were straight-up assertions, but ignore his quite explicit statement that God "wants all men to be saved and to come to a knowledge of the truth" (1 Timothy 2:4).   But if we are going to get our theology out of rhetorical questions, how about these ones:

"Do I take any pleasure in the death of the wicked? declares the Sovereign Lord. Rather, am I not pleased when they turn from their ways and live?....Repent! Turn away from all your offenses; then sin will not be your downfall. Rid yourselves of all the offenses you have committed, and get a new heart and a new spirit. Why will you die, people of Israel? For I take no pleasure in the death of anyone, declares the Sovereign Lord" (Ezekiel 18:23,30-32).

or the question asked by Abraham:

"Will not the Judge of all the earth do right?" (Genesis 18:25).

You see that St. Abraham had full confidence that God would act in a way that he, a mere human being, could understand as being just and righteous.  Abraham's faith was credited to him as righteousness, and God accepted his request.

Or if you prefer the metaphor of the Potter and the Clay, perhaps you can read the passage which St. Paul got it from, about how human choices can avert God's intentions and plans:

Then the word of the Lord came to me.  He said, “Can I not do with you, Israel, as this potter does?” declares the Lord. “Like clay in the hand of the potter, so are you in my hand, Israel.  If at any time I announce that a nation or kingdom is to be uprooted, torn down and destroyed, and if that nation I warned repents of its evil, then I will relent and not inflict on it the disaster I had planned.  And if at another time I announce that a nation or kingdom is to be built up and planted, and if it does evil in my sight and does not obey me, then I will reconsider the good I had intended to do for it.  Now therefore say to the people of Judah and those living in Jerusalem, ‘This is what the Lord says: Look! I am preparing a disaster for you and devising a plan against you. So turn from your evil ways, each one of you, and reform your ways and your actions.’ " (Jeremiah 18:5-11).

If you look at the context of Romans 9, you will see that St. Paul is imagining an Jewish interlocutor who can't accept God's choice to temporarily set aside Israel in the propagation of the Gospel, and to choose the Gentiles instead.  (Notice that Scripture never actually says that Esau and Pharaoh were damned, that's not the point of the passage.)  His rebuke of the insolent question makes sense in this context.  But the actual reason for God's decision does indeed have something to do with Israel's choices, since Paul gives a reason for their failure to be saved: "Why not? Because they pursued it not by faith but as if it were by works" (9:32).  Furthermore God's ultimate purpose in all this is to save the world: "For God has bound all men over to disobedience so that he may have mercy on them all" (11:32).  As the Gospel of St. John states:

"For God so loved the world that he gave his one and only Son, that whoever believes in him shall not perish but have eternal life.  For God did not send his Son into the world to condemn the world, but to save the world through him." (John 3:16-17)

Is the God you believe in the same God who left the 99 sheep in the sheep fold to seek the one sheep who was lost?  "In the same way your Father in heaven is not willing that any of these little ones should perish" (Matt. 18:14).  The God who searched through the house for the one lost coin; the loving father who rescued the prodigal son?  Who commanded us to love our enemies, because that's what he himself does (Matt. 5:44-45)?  Who loved his enemies so much that he sent Jesus to die for the sins of the whole world?  If not, then apparently you are worshipping a different God and a different Jesus.

One more proof-text.  It is this one:

Bear in mind that our Lord’s patience means salvation, just as our dear brother Paul also wrote you with the wisdom that God gave him.  He writes the same way in all his letters, speaking in them of these matters.  His letters contain some things that are hard to understand, which ignorant and unstable people distort, as they do the other Scriptures, to their own destruction. (2 Peter 3:15-16).

This warning label is also in the Bible!  St. Peter identifies the true meaning of Paul's message ("our Lord's patience means salvation"), and then advises people to watch out lest tricky theological topics such as predestination paint a false picture of God, a false picture which he says is capable of destroying you spiritually!  (Some would argue that if God hates certain people, why shouldn't we hate them too?  In this way it is possible to damn yourself using ideas that were falsely wrested from Scripture.)  So apparently we ought to be careful when deciding what the "plain teaching" of Paul's letters is.  At least, that's the plain teaching of this passage.

I don't claim to be "neutral" or "unbiased" in my interpretation of these particular Scriptures, any more than anyone else is.  How could I possibly be unbiased, when you are saying such terrible things about our Father in heaven?  The doctrine that God is good is more fundamental even than the doctrine that the Scriptures are inspired.  So that if it were necessary to choose between them (which it is not!) one should certainly pick the former over the latter.  This is the faith of Abraham, who lived before any part of our current Bible was written.

The Bible may appear to support both sides of this issue, but I have an interpretive key, namely God is love and in him there is no darkness at all and that it is not presumptuous to teach children to sing Jesus loves me this I know, for the Bible tells me so.  These are a foundation for sound, correct doctrine, unlike "plain reading" which immediately runs into difficulties here since many of the plain readings appear to conflict.  There is indeed an important spiritual truth to be found in Romans 9 and every other verse you have quoted, but it is not found in any opinion that makes God out to be morally monstrous.

As you say, this fatalistic doctrine "chills the blood", and "it also repels" you.  There is a good reason for that—the reason is that it is wrong!  "The letter kills, but the Spirit gives life (2 Cor 3:6)"  If you have any guidance from the Holy Spirit at all, trust your instinct that God is good, not just powerful:

One thing God has spoken, two things have I heard: That you, O God, are strong, and that you, O Lord are loving (Psalm 62:11-12).

God is more loving than you can imagine—and also more powerful, since he is capable of making creatures with real freedom and responsibility.

Posted in Theological Method, Theology | 37 Comments

God and Time II: Special Relativity

by Aron Wall Posted on March 7, 2015

Despite what people seem to think, there are very few controversies in Theology where there is decisive evidence coming from Physics (leaving aside some real doozies such as Young Earth Creationism).  But the question of whether God is in Time is one of them.

In the previous post I argued that God must perceive Time as it really is.  But our conception of Time has been modified radically as a result of Einstein's theories of Relativity.  It starts out with Special Relativity, and becomes even more extreme with General Relativity.

The first thing to notice is that our usual division of time into Past, Present, and Future—which I tacitly accepted when discussing the metaphysical problems of the A-theory (a.k.a. Presentist) idea that only the Present really exists—seems to be totally wrong.  Instead you have to think about spacetime, and it is unclear what we even mean by referring to the "Present".  As I said in one of my earliest posts:

We're used to dividing up time into three parts relative to ourselves: past, present, and future. The present is just an infinitesimal sliver, so in a sense this division is into two parts: points to the past have \Delta t < 0 compared to you, while points to the future have \Delta t > 0 compared to you.

However, special relativity tells us you have to chop up spacetime in a more complicated way.  Bearing in mind that you each live in a particular place as well as a particular time, you can chop up spacetime into three different regions.  The future is points that are timelike separated to you and have \Delta t > 0; these are the points of spacetime that you can affect.  The past is points that are timelike but have \Delta t < 0; these are the points that can affect you.  Then there is elsewhere, the points that are spacelike separated.  These points can neither affect, nor be affected, by each other.  The three regions are separated by the "light cone", which consists of the points that you could send a lightray to (or from).  I'm too lazy to draw a picture right now, but you can see a pretty good explanation here

If we treat time as a metaphysically fundamental quality, and say that things at the present moment of time really exist, really we are saying that anything which is simultaneous to my present experience exists.  But the concept of "simultaneous" is rendered problematic in Special Relativity.

That is because there exists a symmetry of spacetime, called a Lorentz boost, which mixes up the time and space coordinates.  (The Lorentz boost corresponds to changing the speed of the "reference frame" in which you are viewing the system.  You can always transform to a frame in which a given object's center of mass is at rest.)

Here is an spacetime diagram of two frames of reference, one in which "Static Sue" is at rest, and the other in which "Mobile Martha" is at rest (despite their names, there's no actual objective fact about which one of them is moving):

Here the vertical axis is time and the horizontal axis is one of the dimensions of space.  The horizontal grey lines indicate Sue's notion of simultaneity, and the diagonal peach lines represent Martha's notion of simultaneity.  Their relative velocity is about half the speed of light, which would travel at approximately 45° had I drawn any light in this picture (I chose not to draw any light because, sadly, both ladies are blind).  Sue and Martha's reference frames do not agree about which of the two events p or q occurred first.

In particular, as long as two points p and q are spacelike separated, by acting with this symmetry you can always choose for their time coordinates to have any of the 3 temporal relations: t(p) > t(q), t(p) = t(q), or t(p) < t(q).  Since nothing can travel faster than light, no causal signals can go between the points p or q anyway, so the order doesn't really matter.

(Nor can we say that if p exists, everything spacelike separated to q exists simultaneously.  For "simultaneous" is supposed to be a transitive relation.  If p is simultaneous with q, and q is simultaneous with r, then p and r should also coexist simultaneously.  But in Special Relativity every pair of spacetime points share a common point they are both spacelike to.  This idea would thus make all spacetime points simultaneous.)

And yet, for some reason, in the very same 20th century in which Physics got rid of the idea of the Present moment, some revisionist theologians decided to propose a more limited, anthropomorphic deity who changes with time, or who doesn't know the future.  Either because they wrongly believe divine foreknowledge conflicts with free will, or because they believe that the Bible teaches this, or because they subscribe to more radical process theology ideas...

But if:

1) God is omnipresent (so he does not pick out a particular point in space), and
2) The Lorentz boost is a valid symmetry of reality, then inevitably:
3) God is omnitemporal.

There are only a few possible rebuttals.  One is to hope that relativity turns out to be wrong in this respect.  There are a few very speculative quantum gravity ideas about this (e.g. Hořava gravity), but none of them are extremely promising.

A second is to say that God just breaks this symmetry, he "picks out a particular reference frame" and that's just that.  Well, in addition to being ugly to theoretical physicists such as me, it seems bizarre that God, who transcends the universe and created it, would need to break a law of nature of that he created just in order to relate to the universe.  (It's not like not we're talking about a miracle here, we're just talking about the way in which God coexists with the universe at every moment.) God relates to the universe by creating it as it is, and by knowing it as it is—which means that there should be no reason to break any symmetries in describing how God relates to the universe, if our best model of how the universe is preserves those symmetries.

A third approach might be to bite the bullet and say that God exists in space as well as time.  Maybe there is one version of God (or should I say "a god"?) existing at each spacetime point, and each god knows only the things in the past lightcone of that point.  So God can't send signals faster than light or know what's going on in the Andromeda Galaxy right now (for any reference frame's definition of "right now").  But what a needless limitation!  I could throw out a prooftext here, but I'm supposed to be saving the Scriptures for the next post.  Instead I will confine myself to pointing out that this view has serious issues concerning the divine unity as well as omniscience and omnipotence.  Is it really necessary for the Blessed Creator to chop himself up into pieces, just in order to create the spacetime continuum?  This seems to tend more towards a Pantheistic view in which the God creates the universe out of his body, then a Monotheistic view in which he creates freely like a novelist inventing a story.

One reader (who subscribes to the "Open Theism" view that God does not know the future) suggests that perhaps God exists in all reference frames.  But this makes no sense to me.  We cannot say that God exists in all reference frames simultaneously, since we need to first pick a reference frame to say what we mean by simultaneous!  Indeed, this view does not really give a well defined answer to the question of what knowledge God has access to at any given moment.  If I, sitting in a particular place and time, pray to God to intervene at some other point, which is spacelike separated to me, can he base his answer on things taking place in the Andromeda Galaxy, or not?  This model would imply that there are infinitely many versions of God at a single spacetime point, each with different knowledge and powers.  That's even more complicated than the previous supposal.  Which version of God gets to decide what happens at that point, and why can't they just all communicate with each other?  This view seems more problematic than any of the others.

So, to conclude, Special Relativity seems to strongly suggest that if God has no definite position in Space, he must also not be in Time.  Now we have Spacetime, and we ought to be able to translate what we say about God into that language somehow, unless we think that our theological expressions should be immune to progress in the Sciences.  But here it is traditional theology, not revisionist modern theology, which fits the data better.

(Although this raises certain questions about other theological entities, such as angels or heaven, which are often conceived of as being in time, but not space.  Or at least not in our space... but of course we don't really know much about what these entities are really like.  Although God transcends all understanding, in certain respects we know a lot less about these created entities than we know about God, because (a) there are no metaphysical arguments that they have to exist, and (b) we interact with them less frequently.)

I've decided to save General Relativity and other physics considerations for another post.

Next: General Relativity

Posted in Physics, Theology | 19 Comments

God and Time I: Metaphysics

by Aron Wall Posted on March 2, 2015

I've been asked to write about the relationship between God and Time.  I believe that God is not a part of Time, that he is eternal and unchanging, and that therefore he knows (what we consider to be) past, the present, and the future equally.  I believe that there are good reasons to believe this coming from 3 different fields of study: 1) metaphysics, 2) physics, and 3) biblical theology.

(Of course, it is also true that the Son of God

came down from heaven and was incarnate by the Holy Spirit and of the Virgin Mary, and was made man.  He was crucified for us under Pontius Pilate, suffered [παθόντα, which can also mean "was passively acted upon"] and was buried.  On the third day...

In other words, he united himself to a human being who was, like us, part of the flow of time.  In this sense, God is in Time, but to allow this to be truly and properly a life-giving paradox, we need to assert that it was the Eternal and Immortal who suffered and died for us.  The more we anthropomorphize the divine nature, the less significant is the Incarnation.)

In order to address this question, we need to know two things: what is Time and who is God?  To some extent we can begin to explore the metaphysics of Time without discussing who God is, although eventually we must place every created thing in the context of the One who created it.

So let's start with Time.  There are two main views on this, which are rather boringly called the A-theory and the B-theory (although there are variants I won't consider).  This is, as far as I can tell, due to a 1908 article by the philosopher John McTaggart arguing for the Unreality of Time.  McTaggart was basically a Hegelian mystic and yet, despite the later backlash against Hegel in the subsequent era of Logical Positivism, this paper has became one of the foundational articles for contemporary Analytic Philosophy!

(Recently I've been reading the records of the Oxford Socratic Club, a club for debate between Christians and Atheists/Agnostics, of which St. Lewis was President, whose Digest has recently become available from Lulu thanks to St. Joel Heck.  The talks were given around the time of WWII, which was a particularly interesting time for Philosophy since it was during the overlap period when both Idealism and Logical Positivism were taken seriously.)

Anyway, the A-theory (a.k.a presentism) claims that time flows from the past to the future, in such a way that neither the past and future really exist, but only the present moment is real.  However, the past was real and the future will be real, since time is really flowing from past to future.

The B-theory (a.k.a. eternalism) claims that all times (past, present, and future) exist equally, and that the word "present" is like the word "here", an index to refer to the location of the speaker within the timestream.  Thus, there is no objective fact about which time is really "present", any more than there is an objective fact about whether "here" is located in the USA or Australia.

One of my commenters explained the difference in this way:

The first is called the A-theory, or tensed time. Only the present is real; the past and future do not exist. The second is called the B-theory, tenseless time, the block view of timespace, or Minkowski or Minkowskian spacetime. All of time—past, present, and future—is complete and actual in this view. In some unperceived way, all of time is occurring now.

I mostly agree with this statement (although I'm not sure what "complete" means) but take issue with the last sentence.  The B-theorist would not say that all of time is literally now anymore than we would say that all places are here.  The past indeed exists, but does not exist "in the present" because for an A-theorist that means "at the same time as the speaker is located."

Really what that last sentence does is explain the B-theory view in terms of the A-theory view.  According to the A-theory view, only the Present moment is real.  Saying "all times exist now" is really shorthand for "The B-theorist ascribes to the Past and Future the same type of reality which the A-theorist only ascribes to the Present."

Can we return the compliment and describe the A-theory in terms of the B-theory?  Actually we cannot.  If all you have are B-theory ideas, there is no way to make the A-theory clear.  If an A theorist says that the past does not yet exist, the B-theorist will translate "does not yet exist" to "exists at a moment t_1 previous to the current moment t_2", and if he says that the future is going to exist, she translates this to mean just that the future is in the future!

In this sense the A-theory contains a vicious circle in it, as pointed out by McTaggart (although I don't agree with his conclusion that time is therefore "unreal").  When we say that a physical object is changing or flowing, this means that it changes with respect to time, that if we plotted it out on a graph, there would be a physical parameter x such that the time derivative is nonzero: dx / dt \ne 0.  When we say that time itself is flowing, either we mean dt / dt = 1 (time goes at one second per second) which is a trivial calculus tautology which says nothing, or we mean that it is flowing with respect to some other meta-time coordinate.  But that's absurd, if we can only explain time with respect to a deeper time.  (And if that deeper time "really flows" we will need a 3rd timestream to parametrize that, and so on.)

It's like those time travel stories where somebody goes back and changes the past.  But if you think about it, that's a crazy contradiction.  Time just is the way we parametrize change.  The moments of time cannot themselves change or flow in the same way that things change or flow, since there is no other timestream to parametrize their change.  (Well, maybe in science fiction there is, but in the real world there's no reason to postulate this.)

We can put it another way.  The A-theorist maintains that the past and future do not exist.  But if this is true, it is impossible to distinguish it from a radical presentism in which one maintains that only the present moment will ever exist.  Suppose that right now (e.g. 9:18 pm March 2, 2015) is the only instant that will ever exist.  The past is just a delusion of our memory, and the future is a just delusion of anticipation.  None of it is real.  Clearly an absurd form of skepticism.  But really, the A-theory implies this.  For it says that the future exists only in the future and that the past exists only in the past and that both of these are forms of nonexistence.  So the future does not really exist, and neither does the past.  No amount of protesting about the fact that the future is going to exist or the past having existed implies anything about it actually ever existing, unless you secretly smuggle in the B-theory view that these modalities refer to ways of existing.

One might worry, though, that the B-theory is radically foreign to our own experiences.  Whatever we say philosophically, isn't it obvious if we inspect our own conscious experiences that it feels as if time is ever flowing and changing?  Each moment is so slight that we hardly grasp it before the next is upon us.

I admit that this worry has some psychological tug on me, but in the end I don't think it implies the A-theory.  After all, it also feels as if my own experiences are more real than the experiences of others, and that here (wherever I am) is more real than there (wherever I am not) but these things I am happy to discount as illusions, without incorporating them into my metaphysics.  Furthermore, my brain cannot really detect a single instant: it takes a second or two for me to consciously process my sensory data.  Thus what I experience as now is always really a moment that has a finite amount of thickness in time.  If only the a single instant existed at once, that sliver would actually be too small for any conscious experiences to fit inside of it.  But if more than one instant can exist, it is simplest to say that they all exist, but that my self simply does not experience them all together in one lump.

Thus I conclude that only the B view makes logical sense.  Some might say that this means Time is an illusion; but I would instead say I am asserting that all of Time is real.

Now if God is omniscient, then he experiences everything as it actually is.  But we have seen that the idea that time itself "flows" and "changes" (as opposed to saying that things change with respect to time), makes no sense.  If the B-theory is correct, then God must experience it as being correct, that is he must himself be eternal and unchanging.

But this is also what we would conclude if we instead started with the nature of God as understood by classical theism.  Here, you will recall, God is conceived of as the fundamental being whose existence is explains everything else.  As I argued before, the fundamental reality, however we conceive of it, must be eternal:

If the fundamental entities are necessary, then it stands to reason that they are also eternal, since something that exists necessarily cannot come into being, or cease to be, or indeed change in any way.  They must just exist timelessly.  Besides which, if they explain what happens at all moments of time, it doesn't seem plausible that they should only exist for certain moments of time.  For similar reasons, one can argue that the fundamental entities can't be limited to just one region of space.  Their influence must be present everywhere.

For God to be in Time, would mean that there is a part of God which changes and develops and changes, even if it is only the part that observes "what time is it right now".  But that would mean that God is actually divided into pieces, some of which (the past versions of God) help to explain others (the future versions of God).  This is inconsistent with the unity and eternity which befits the divine nature, which is fully real and cannot pass away like shifting shadows.

This is why proponents of Classical Theism have generally maintained that Time, rather than being some Metaphysical Ultimate, is actually part of created reality.  It exists contingently as part of the physical world, because God created it.  This view was developed by Philo, St. Augustine and others, but in the next post two posts we shall see that it is also supported by modern physics: especially Einstein's theories of Relativity.  Then in the third last post posts I will argue that the view that God is eternal and unchanging is also to be found in the Bible.

Next: Special Relativity

Posted in Metaphysics, Theology | 73 Comments