The comments to my post about the Hard Problem of Consciousness have spiralled into a long conversation about the Problem of Evil, Free Will, and whether God is in time, and whether God knows the future. I won't try to recap that discussion here (you can go read it yourself if you like), but instead to answer some questions about which were raised, which I had been postponing answering due to being busy with work and job interviews.
St. Steve asks:
How likely or unlikely is that there is something like free will? I read that most contemporary philosophers argue libertarianism, I have also seen that there is a point of view Compatibilist. What do you think is the most plausible?
It seems that those who support the libertarian free will are all dualistic, while a point of view is Compatibilist is a non-reductive materialism of mind.
What is your opinion on these views of free will?
"Libertarian Free Will" is the position that human beings (and maybe other entities) have the ability to make genuine decisions, which could have been otherwise, and that the causal responsibility for that decision is rightly attributed to that person. Causal responsibility must of course be distinguished from moral responsibility, which requires additional factors, such as the person being aware of the consequences of their decision.
"Determinism" is the contrary position that everything we do is determined by certain factors outside of our control, such as God or the laws of physics or our genetic predispositions or whatever. As you can see, there are both theological and materialistic versions of this idea.
"Compatibilism" is the compromise belief that although determinism is true, we nevertheless should be regarded as morally responsible for our actions, because we have a lesser, non-libertarian form of "free will". In other words, even if it was inevitable that we did what we did, because we wanted to do it, and nobody put a gun to our heads, we are (in this view) still morally responsible. ("Morally responsible for what purpose?", one might ask. A human justice system may reasonably disregard these metaphysical issues, but responsibility before God, who sees everything, plausibly does depend on such things.)
Well, it seems to me that compatibilism is a namby-pamby watered-down use of the word free will. When I say Free Will, I mean the full-blown libertarian kind! Now let's ask if it exists.
The first consideration is experiential, somewhat along the lines for my argument for morality. A lot of the time, it feels like we have free will, the ability to make choices and do otherwise than we did. (In other cases, like sneezing, we feel like we had little choice about the matter.) I think this is substantial prima facie evidence for the existence of Free Will, but it is not conclusive. It is not a logical contradiction to feel like you have Free Will when you don't, the way it IS a logical contradiction to feel like you are Conscious when you are not.
Susan Blackmore claims that she no longer feels like she has free will, but this seems like self-hypnosis to bring her experiences in line with her philosophical beliefs. (By the way, I highly recommend her book Conversations in Consciousness, in which she interviews many leading thinkers about what consciousness is.)
The second consideration is Science. Now the laws of Classical Physics were deterministic, meaning that if you know all the positions and momenta of all the particles at one moment of time, you can deduce what happens at any other moment of time in the future or the past. Since most people think they have very limited control over what happened before they were born, this served as a powerful argument against Free Will, at least for Materialists. (A Dualist or an Idealist could of course evade the conclusion by denying that the laws of Classical Physics give a complete description of the world.)
Nowadays we know that Classical Physics is false. Quantum Mechanics appears (at least for all practical purposes, leaving aside Many Worlds and other bizarre interpretations) to be nondeterministic. The outcome of a given experiment can only be predicted statistically, in terms of probabilities. Oddly, this has not resulted in much resurgence in a belief in Free Will, perhaps because it was under attack during the 20th century for other reasons, perhaps because the spotlight has moved on to neurological and psychological considerations.
On a more philosophical note, some might say, if chance determines what I do, that isn't any better than if something beyond my control does it. How is it me acting if my decisions are just a roll of the cosmic dice?
But I think this is based on a confusion. Chance is not an entity any more than fate is an entity. Suppose the laws of physics absolutely required a certain big rubber ball to knock over a glass of wine. It would still be the ball that did it, not fate. Similarly, if your decisions can only be predicted probabilistically, it is still you that does it. The probability is just a measure of how likely you are to do it.
Another possible objection is that the brain is made out of parts. Well before you get to the level where quantum physics is relevant, the parts are small enough that they cannot meaningfully be said to be conscious. A neuron probably does not have mental states (and even if it did, it wouldn't be the same thing as our mind). Certainly atoms have nothing like a mind, that we know of. So even if the atomic motions involve indeterminism, it can't be credited to us; the atoms still control what we do.
At one time this reductionistic argument bothered me quite a bit. However, behind this argument is a strange double-standard. We are to be sufficiently identified with our atoms that we have no identity above and beyond them. And yet, not so identified with them that if the atoms act freely, we act freely. A strict materialist would have to say: I am the atoms I am made out of, and therefore there can be no question of them controlling me as if they I were something else. (On the other hand, if I am something else in addition, who is to say that this something else cannot act in the world?)
Again, the reductionistic argument basically supposes that parts are the only things that are really real, and wholes are just meaningless arrangements of parts which have no real identity or status. But clearly my whole self does exist; what's more it has the rather surprising property of consciousness, which I would not have predicted from the parts alone. If wholes are sufficiently real that they can be conscious, why can't they be real enough to act freely?
Indeed, if the reductionists are right that the whole is identical to its parts, it is equally true (since identity is a symmetric relation) that the parts are identical to the whole. So their behavior is determined by what I do. Thus even a Materialist could perhaps believe in Free Will.
Clearly this is a deep problem, and not one that can be easily resolved by a superficial appeal to Science or Logic. My reflections here are intended to produce aporia, the type of confusion induced by listening to Socrates, who was the wisest of men because at least he knew he didn't know. And, in the absence of knowledge, he fell back on myths about the gods, to explain the moral convictions that were the foundation of his entire project. Those who have read Plato will know what I am talking about.
So at the end of the day, I fall back on my religion for deciding what to believe about Free Will. The fact that God—who knows our inmost being—relates to us as if we were morally responsible creatures who can make real choices, is for me the most decisive indication that we really are. (Of course, the Bible also talks about divine predestination. I believe these passages also describe an important truth, one that is also important to my religious experience. Even if we cannot easily reconcile all of these truths with our puny brains!)
St. Luke P writes:
I appreciate your affirmation of free will and it sounds like you think it is important. I think that it is essential for moral responsibility. Furthermore, free will must be more than a set of counterfactuals about what we would do.(I know this is not your view) Indeed, such a set of counterfactuals could describe a computer which has no free will at all. Rather, to have free will we must truly have "the ability to do otherwise" in these situations. I am blameworthy for giving into temptation in virtue of the fact that it was morally wrong to do so and I had the ability to do otherwise.
Now you say that foreknowledge is not at odds with free will but I think it must be with respect to this kind of free will. If I could genuinely choose X or Y then there must be no "fact of the matter", as you say, about which I will choose. Will implies must.
I understand that you affirm the B theory of time. This is where I think there is a real conflict with free will. The B theory implies that all time is equally real and that the future exists. If the future does exist, as described by the B theory, then all of the facts of the matter are fixed and unchangeable.
Thanks for your comment. I like your phrasing that "The B theory implies all time is equally real and that the future exists", because it avoids the common pitfall of saying that all times exist "now", which true only if we use the word "now" metaphorically. (To say that all places exist equally, is different from saying that all places exist here. On the B theory, the word "now" functions similarly to the word "here".)
But I don't agree at all that free will requires there to be no fact of the matter about what we choose. The only way there could be no fact of the matter, is if the choice isn't made at all, which is the opposite of free will!
There is a fact of the matter about whether I chose to marry my wife St. Nicole, and an observer can know that fact with certainty, but that does not make the decision retroactively unfree. I cannot now change this decision, but my past self could have done otherwise.
When you say "fixed and unchangeable" this equivocates between two meanings of the word fixed. The facts of existence are fixed in the sense that they are definitely real and have a precise nature. In that sense, our choices are fixed. But that is compatible with saying that there are other possible outcomes, which could have existed instead.
And of course, if our future decisions are real, then God can know them in advance. (See here for a general solution to most supposed paradoxes involving Divine Omniscience.)
Added Later: Note that, in Quantum Mechanics, it is also true that "if you know all the positions and momenta of all the particles at one moment of time, you can deduce what happens at any other moment of time in the future or the past". That's because the first part of the sentence is impossible, by Heisenberg's uncertainty principle!

From my lay mans knowledge of logic, I believe St. Luke P committed a common fallacy in modal logic, when saying that P is true necessarily, the detractor who commits the fallacy erroneously states that necessarily P. Or in other words the detractor states that since P is a necessary outcome of a certain state of affairs, then P is a necessary truth in the strong logical sense, but P can be a necessary outcome of a contingent state of affairs leaving P ultimately contingent.
In modal logic notation, one uses the symbol (\boxempty in latex) to mean necessarily. Then what you are saying is that
(\boxempty in latex) to mean necessarily. Then what you are saying is that
1.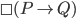 (Necessarily, if P then Q).
(Necessarily, if P then Q).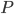 (P is true)
(P is true)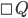 (Necessarily, Q)
(Necessarily, Q)
2.
while it implies Q, does not imply
3.
For that deduction you would need either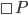 or
or 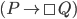 .
.
Interesting post but I have to notice that quoted commentator made some errors. Some recent polls show that most contemporary analytic philosophers in Western academia are compatibilists about free will even there are big libertarian minority and Free Will skeptics minority.
Also, dualism and libertarianism are not necessary connected. Probably, many dualists are libertarians but not all and certainly not all libertarians are dualists about mind. For example, Peter van Inwagen , distinguished analytic philosopher, is materialists about human persons (even if he is not naturalist, he is notable Christian philosopher) but also believe that we have genuine, libertarian Free Will. Robert Kane defend robustly libertarian Free Will in his writings (and his introduction in contemporary debate about Free Will is really great) but I don't think that he is dualist.
I believe that theists should not reject compatibilism as inconsistent with theism (even if they reject compatibilism on some other ground, because there are very strong and intuitive arguments against this view). Recently philosopher Michael Almeida propose controversial thesis that theism and libertarianism are incompatible thesis!
Exactly Dr. Wall, thanks for the clarification in symbolic form.
One clarification, I wouldn't say that □P→□Q or that necessarily P entails the necessity of Q. Q can still be a contingent fact even though it necessarily follows from necessarily P. So for example Gods foreknowledge is necessarily true, but his foreknowledge is of contingent facts about future human decisions. So let P be God's foreknowledge of Q and Q be a free choice (libertarian) made by a person. So
1. □P→Q
2.□P
3.Q
is correct, but the fallacy is committed when someone concludes necessarily Q... (therefore no free will.)
1. □P→Q
2.□P
3.□Q
John,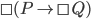 .
.
You have to be sure to put the parentheses in the right place when you write these expressions, and I don't think you have it quite right. In your first sentence I think you meant
If P is the proposition that God knows I will go to work tomorrow, and Q is that I go to work tomorrow, then the correct deduction is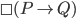 , not
, not 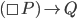 (If P is necessary, then Q) is not correct. (The convention is that
(If P is necessary, then Q) is not correct. (The convention is that 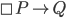 means the latter, not the former.)
means the latter, not the former.)
Thus although your first syllogism is indeed valid, I don't think either of its premises are true. If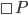 were true, then together with
were true, then together with 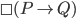 it would imply
it would imply 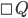 , denying free will. The solution is to deny both
, denying free will. The solution is to deny both 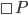 and
and 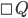 , while affirming
, while affirming 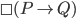 .
.
Miloš,
Thanks for your comment. I agree that ones position on Free Will is not obviously connected with ones position on Materialism/Dualism.
I think St. Michael Almeida's thesis is controversial because it is wrong...
Hmmm...I guess what I'm trying to affirm is that God's foreknowledge is necessarily true and the free act is contingent, not that God's foreknowledge entails actions necessarily. I don't think that God's knowing future actions means the person necessarily performs said action. In fact I think the opposite is true, that a person's free action is what grounds God's foreknowledge necessarily. The only way I know how to justify this is by asserting that God's omniscience entails middle knowledge of counterfactuals. So where you and I disagree is like you said, where we place the parentheses. I would say (necessarily P) entails Q, without adding that necessarily (P entails Q).
Sorry I couldn't type the symbolic forms, I'm typing on my kindle and it's not working with me.
John,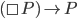 (If P is necessary, it is true), it follows that your statement that
(If P is necessary, it is true), it follows that your statement that 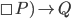 , while true, is logically weaker than the (more obvious and more relevant) statement that
, while true, is logically weaker than the (more obvious and more relevant) statement that 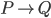 (If God knows I will go to work, then I will go to work). That follows from the fact that God is never wrong. This in turn is weaker than the statement than
(If God knows I will go to work, then I will go to work). That follows from the fact that God is never wrong. This in turn is weaker than the statement than 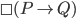 (*), which follows from the fact that God cannot be wrong. So my statement implies yours, but yours does not imply mine. So your premise 1 is true, but not as strong as it might be.
(*), which follows from the fact that God cannot be wrong. So my statement implies yours, but yours does not imply mine. So your premise 1 is true, but not as strong as it might be.
Since
On the other hand, your second premise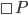 is simply false. If I have Free Will, then
is simply false. If I have Free Will, then 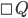 is false, but
is false, but 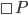 together with the statement that God cannot be wong
together with the statement that God cannot be wong 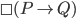 would imply
would imply 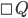 . In other words, there is a possible alternative world in which I don't go to work, but in that world God does not know that I go to work (because I don't) and therefore
. In other words, there is a possible alternative world in which I don't go to work, but in that world God does not know that I go to work (because I don't) and therefore 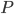 is not true in all possible worlds.
is not true in all possible worlds.
I'm not a fan of middle knowledge, but it's not necessary to reconcile God's foreknowledge with free will. I would say that when we say God's foreknowledge is "necessary" we are using a verbal circumlocution to mean that necessarily, anything God knows is true. There is no reason to say that a given act of foreknowledge is itself absolutely necessary; it can be contingent on the thing known actually being the case.
(*) at least, it is weaker if we use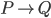 to mean material implication, which is true iff Q is true and/or P is false. But I see from Wikipedia's list of logical symbols that it is more usual to use
to mean material implication, which is true iff Q is true and/or P is false. But I see from Wikipedia's list of logical symbols that it is more usual to use  or
or  for material implication, and
for material implication, and  for logically entails. If we interpret
for logically entails. If we interpret  as logically entails, then since logic is itself necessary,
as logically entails, then since logic is itself necessary, 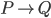 would be equivalent to
would be equivalent to 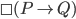 .
.
I believe I'm coming to a better understanding of what your claim is, but I still disagree with □(P→Q) (since God is never wrong, then Q). From my understanding of knowledge, knowledge of a free choice must be grounded in the facts of the free choice. It seems to me when you state "(If God knows I will go to work, then I will go to work)" the antecedent is being grounded in the consequent and becomes circular. This is why I don't think it is correct to state □(P→Q).
Now when I state (□P), I don't mean "necessarily, anything God knows is true" I just mean that in all possible worlds God knows every contingent free choice of all possible worlds. So to say that □P entails □Q given □(P→Q), is false because □P does not entail □(P→Q). which is what you stated when you said " I would say that when we say God's foreknowledge is "necessary" we are using a verbal circumlocution to mean that necessarily, anything God knows is true." Which is not what I meant by □P.
I see my error, thank you for you patience
John,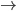 (entails) nor
(entails) nor  (material implication) make any claim about "grounding" or causality. They merely state a logical relationship between the propositions P and Q, that if P is true, then Q is true. (In addition,
(material implication) make any claim about "grounding" or causality. They merely state a logical relationship between the propositions P and Q, that if P is true, then Q is true. (In addition, 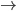 states that the implication is logically necessary.)
states that the implication is logically necessary.)
I think the issue primarily comes down to the definition of the symbols used in modal logic. I agree with you that God's knowledge of our choices is grounded in the fact that we make those choices. But neither of the symbols
As an example,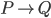 is true if:
is true if:
1) P is that a cop correctly testified I was speeding, and Q is that I was speeding (in which case Q is the cause and P is the effect)
2) P is that I truthfully promised I would go home, and Q is that I did (in which case P is the cause and Q is the effect)
It doesn't say anything about which proposition grounds the other (or whether both are grounded by some third thing).
Secondly, symbols like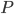 are interpreted to mean that the proposition
are interpreted to mean that the proposition 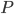 is true in the real, actual world. They are not generally interpeted as Molinist "middle knowledge" style counterfactuals (which would incidentally require a more complicated system of symbols to express, than classic modal logic). By
is true in the real, actual world. They are not generally interpeted as Molinist "middle knowledge" style counterfactuals (which would incidentally require a more complicated system of symbols to express, than classic modal logic). By 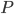 I meant that in the actual world, God knows that the actual me will go to work in the actual world. Not anything about God knowing what I would do in some possible world. (I don't believe in Molinism, but that is irrelevant to my claims about the standard interpretation of the symbols in modal logic.)
I meant that in the actual world, God knows that the actual me will go to work in the actual world. Not anything about God knowing what I would do in some possible world. (I don't believe in Molinism, but that is irrelevant to my claims about the standard interpretation of the symbols in modal logic.)
On this interpretation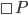 can only be true if, in every possible world X, I exist in X and go to work in X and God knows it in X.
can only be true if, in every possible world X, I exist in X and go to work in X and God knows it in X.
If the thing that grounds P is a contingent free choice, then P must be contingent as well.
One question, if the interpretation of quantum mechanics is deterministic then the objection against free albeldrio for materialists still possible?
Charles,
I take it "albeldrio" means will...
There are many philosophical issues involved in determining the conditions required for Free Will. But my answer is no. Free will is not possible if both of the following are true: a) the laws of physics are deterministic, and b) the laws of physics give a complete description of human behavior. (Aside from bizarre scenarios in which human choices affect the initial conditions of the universe.)
But there are a number of mathematical theorems which show that (given some reasonable sounding assumptions) there is no way to account for quantum mechanical randomness using "hidden variables" which secretly determine the outcome. Many worlds is different in that it says that anything which can happens, happens in some world. So if that were true, the correct statement is that any time you make a decision, you must make every choice. That's not Free Will.
Aron,
One question, if human consciousness can not be inferred only from the laws of physics, that means it is possible that part of our thinking is not determined by these laws ?(assuming that the laws of physics are deterministic)
Charles,
If by "possible" you mean logically possible (leaving aside plausibility), then sure, I don't see any contradiction with saying that there are deterministic laws of physics, but in addition something else mental which is not deterministic.
However, intuitively we think that our thoughts and decisions are capable of influencing the physical world around us. If so, these (hypothetical) deterministic laws of physics would have to be suspended or inapplicable somewhere in the brain, which seems a bit queer.
At the other extreme, there is another view called Epiphenomenalism which asserts that, even though consciousness is not deducable from the laws of physics, nevertheless the physical state of our brain determines our conscious experiences, and that in turn consciousness has no effect on the physical world. On this view physics controls mind but not the other way around. If that were true, deterministic laws of physics would imply we have no Free Will.
Have an opinion about the dilemma of determinism which indicates that free will is logically inconsistent because it is not compatible with determinism nor indeterminism http://en.wikipedia.org/wiki/Dilemma_of_determinism
Lewis,
That's what I was trying to address with the 2 paragraphs beginning with "On a more philosophical note..."
I claim that Free Will is compatible with Indeterminism. Things which are random in the sense of being unpredictable, are not necessarily random in the sense of having no entity which causes them. In other words, not all causation needs to be determinisitic.
Galen Strawson he argues that the notion of free will leads to an infinite regress and is therefore senseless. According to Strawson, if one is responsible for what one does in a given situation, then one must be responsible for the way one is in certain mental respects. But it is impossible for one to be responsible for the way one is in any respect. This is because to be responsible in some situation S, one must have been responsible for the way one was at S−1. To be responsible for the way one was at S−1, one must have been responsible for the way one was at S−2, and so on. At some point in the chain, there must have been an act of origination of a new causal chain. But this is impossible. Man cannot create himself or his mental states ex nihilo. This argument entails that free will itself is absurd
Lewis,
I don't buy the premise that "to be responsible in some situation S, one must have been responsible for the way one was at S−1."
His argument presupposes that there is no such thing as "agent causality", something which is caused by a thing instead of a situation. That is, even if you have no control over who you are at time S-1, that person at S-1 can still decide between two or more possibilities for who you are at S. If this happens in a nondeterministic way, then you have Free Will. And it's not ex nihilo at all, except in the way that Indeterminism always is.
An alternative principle is "Any time something might or might not happen, there must be some actually existing thing(s) which causes it to be one way or the other." That principle (which is plausibly the opposite of allowing ex nihilo events), plus Indeterminism, implies that at least some entities possess freedom.
Thanks for your answers. I would like to know what is your opinion about the views of Schopenhauer and John Locke on free will. Locke believed that the will could not be free, as each choice is necessarily done, so we can not change
Another question, what answer would you give to Why did one choose A and not B?
Compatibilist philosophers have argued that Free Will Involves Determination and is Inconceivable Without It . Our will and actions are adequately determined, by our reasons, motives, feelings, etc., not in any way pre-determined from before we begin thinking, evaluating, and selecting one of the alternative possibilities in our thoughts. It is our thoughts and the open future that are undetermined.
Others argue that If the choice of A was the reasonable outcome of my deliberation, then the choosing otherwise (the choice of B), which may have occurred given the same past circumstances, would have been "arbitrary," "capricious," "irrational," and "inexplicable," relative to my prior deliberation.
Aron,
Great site and excellent discussions which are, however, generally far over my head. However, there is the free will question where, I think, I can make some contribution.
You say
"However, intuitively we think that our thoughts and decisions are capable of influencing the physical world around us. If so, these (hypothetical) deterministic laws of physics would have to be suspended or inapplicable somewhere in the brain, which seems a bit queer."
To me, it is not clear that even animal behavior is perfectly captured by the laws of physics.
Aquinas says somewhere to the effect that
Stones (i.e. inanimate bodies) move by necessity, the sheep (i.e. animate bodies) move by instinct and
people (i.e rational animals) move by deliberation.
Now, the laws of physics may be defined or understood as the laws of necessity by which the inanimate bodies move. Now, the animals and the people have material bodies and CERTAIN aspects of these bodies
are describable by the laws of physics. This would hold for all material bodies, even inanimate. There may be certain aspects of inanimate bodies that are NOT describable in physics. For the laws of physics describe those aspects of material bodies that can be formalized, in other words, the quantitative aspects, leaving the qualitative aspects of the material bodies outside the domain of physics.
Now, the qualitative aspects of inanimate bodies turn out to be unimportant, generally speaking, in describing their motion, but for animate bodies, these aspects are crucial and hence the entireity of the motion of animate bodies is not describable by physics.
This is my understanding at present and I would love to have your comments.
Mactoul,
In my answer to Charles, I was assuming for the sake of argument that these hypothetical laws of phyiscs are determinstic (contrary to fact since the real laws of physics are quantum mechanical). For concreteness, let us imagine that:
1) The physical universe contains a collection of particles. are simultaneously well-defined, and
are simultaneously well-defined, and , the laws of physics allow you to calculate (by some definite mathematical rule) the positions and velocities at any other moments of time
, the laws of physics allow you to calculate (by some definite mathematical rule) the positions and velocities at any other moments of time  .
.
2) The positions and velocities of the particles at a given time
3) Given the positions and velocities of the particles at one moment of time
where assumption #3 is Physical Determinism, which some people used to think was true back in the days of classical mechanics. It presupposes #2 (which seems to be false in QM). #1 is just for simplicity (I don't want to worry about relativity or field theory here, because I don't think they change anything essential).
Now I think you are asking me to suppose the following:
4) A given physical body has both quantitative and qualitative aspects, which are distinct.
5) The quantitative aspects include the positions and velocites of the particles out of which that physical body is made.
6) The qualitative aspects include (in the case of animals or people) certain mental properties including the capacity to make choices, based on instinct or deliberation, which are not determined by the positions and velocities of particles beforehand.
7) The initial positions and velocities of the particles, prior to the existence of the animal or person, are also not affected by the choices of the animal or person. (This seems pretty obvious but is necessary to close a loophole).
8) At least sometimes, these free will decisions influence the motion of the animal or person.
I am sympathetic to assumption #4 (in the real world, not just this hypothetical determinstic world). But surely at this point we have a contradiction, because if #4-8 are true than #3 is not true. Thus Determinism would be false.
Now perhaps you would be willing to bite this bullet (especially since Determinism seems to be false in the real world). And perhaps this was the entire point of your comment, to deny Determinism. But I think it is worth pointing out explicitly, that this system of affairs would at some point require a "violation" of the quantitative laws of physics (somewhere in the animal's brain?) that seem to be valid outside of animals. That is, you cannot simply partition the universe into quantitative and qualitative aspects; if at some point the qualitative aspects affect the quantitative aspects, then you need to somehow add some sort of extra force term or something to your laws of physics which depend on free will. (In this hypothetical deterministic setup).
Going back to the real world, the laws of QM are not deterministic so there is probably some more wiggle room to postulate that weird things are going on without violating the observed laws of physics inside of animal brains. Also, no one has ever measured the known laws of physics breaking down inside animals, but I suppose a dualist could argue that the physical brain is such a complicated system that perhaps we wouldn't have noticed. Assuming of course that it's subtle; if it involved e.g. gross violations of conservation principles, we would probably have noticed it by now.
I think that this kind of dualism, which violates the usual laws of physics, is slightly implausible, but NOT so wildly implausible as metaphysical naturalists make it out to be. Since there is at least one thing associated with the brain (consciousness) which we can't explain from the laws of physics alone, it seems plausible there may be other things going on as well.
I would replace your (1)
1) The physical universe contains a collection of particles
by
1`) The universe is the totality of consistently acting (and interacting) things.
That is, I do not presume atomism. Now, these things are either inanimate or animate. Physics describes the metrical properties of things, whether determinstically or non-determinstically.
But the properties of animate things are not exhaustively described by physics. This is true even if we hold to strictly deterministic physics. It is the assumption of atomism that is smuggled in, more or less unconsciously, we have to struggle against.
The animate things are wholes and thus entirety of their behavior is not describable by their component parts. Thus, determinism may hold and free will as well. Indeed, free will depends upon the inanimate world behaving predictably.
Free will is applied to human acts. And what are human acts, properly speaking?. They follow deliberation in human minds. The mind perceives what should be done and we either do it or we don't.
This freedom we have, to do or not do our intellect tells us that should be done, isn't this freedom called free will?
It does not seem to have any discernible connection with atoms, determinism or in particular, quantum mechanics.
Mactoul,
I intended my (1) to be compatible with the existence of things other than particles. That's why my (1) didn't say the universe contains ONLY particles. It is still true that if the laws of physics seem to take the form of determinstic rules for what the particles do, then those particles form a closed system. If the atoms are not a closed system because of animals and people, then those (hypothetical) deterministic laws of physics need to be violated at some point.
But even if we ignore issues of free will, I agree that the universe is more complicated than a collection of atoms. Ignoring gravity, it is really described by a relativistic quantum field theory--the Standard Model--which is not deterministic, but it does determine the probabilities of various events via a set of precise mathematical equations, that I know and could write down for you, except it would take too long to explain them. Do you think that these rules of relativistic field theory break down inside of the human brain, which does after all seem like a material object to external observation (even if it may be other things in addition)? Yes or no?
(Neither answer is going to spring a trap, I just think your viewpoint would be clearer if you pick a side on this. Of course "I don't know" is also an reasonable answer, if not as fun...)
Of course, I don't know. But I want to point out some overlooked assumptions.
CS Lewis in Miracles does argue for breakdown in the laws of physics in brain--the Argument from Reason that concludes that naturalism must be false.
I argue that it may even not make sense to apply laws of physics to living bodies in the first place.
Philosophically, a living body is a whole, a "substance" as it is called. Its parts, atoms for instance, are said to exist virtually (not in the sense of this term in physics but in its philosophic sense).
The language used by physicists is, generally speaking, very vague. Indeed, I have not been able to find a single demonstration of Heisenberg's uncertainty principle that was clear enough to understand the very claim.
The quantum field is regarded as the fundamental building block of the universe. But what is a quantum field? It gives the probability amplitude for finding a particle at position x,y,z, at time t. So, surely the particle whose probability is being discussed is more fundamental.
Anyway, what I suspect is, when a physicist does measurements on atoms or electrons inside a living body, and when a chemist does measurements of molecules inside a living body, he will not find any discrepancy. But the overall behavior of the living body as such will never be captured by physics or chemistry.
It is, indeed, overly ambitious to talk about living bodies. Even the reduction of chemistry to physics is problematic enough and may never be accomplished, again for the reason that chemical substances are a whole in their own right. For instance, take a spoonful of liquid water. Is it H20? No. H20 is merely the chemical formula for a water molecule. Obviously, a spoonful of water is not a water molecule. So, even the chemistry captures but a facet of the whole that is a spoonful of water. And, the H20 molecule. Does it contain hydrogen and oxygen? It certainly does not contain hydrogen and oxygen gases. It does contain hydrogen and oxygen atoms in a virtual sense.
Mactoul,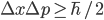 where
where  refers to the standard deviation of a position coordinate
refers to the standard deviation of a position coordinate  and its associated momentum
and its associated momentum 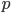 .
.
On the contrary, the Heisenberg Uncertainty Principle is a completely sharp and precise statement, which can be proven mathematically! If it seems obscure to you, that may be because it is written in the language of mathematics rather than in English. The English words are just a vague way to reference the actual statement
That is, you take the probability distribution for detecting the particle in a given location, as obtained from the wavefunction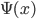 using the Born rule. You can calculate the average position in which it is detected, i.e. the expectation value
using the Born rule. You can calculate the average position in which it is detected, i.e. the expectation value 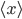 . Then
. Then 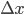 is a measure of how wide the uncertainty is spread around that average position. You calculate
is a measure of how wide the uncertainty is spread around that average position. You calculate 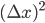 by taking the average value of
by taking the average value of 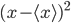 , and then you take the square root of that to get
, and then you take the square root of that to get  .
.
Then you take the Fourier transform of the wavefunction to get the wavefunction with respect to momentum,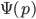 . You repeat all the steps above to calculate
. You repeat all the steps above to calculate 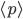 and
and 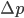 . At the end of the day, the product of the two numbers
. At the end of the day, the product of the two numbers 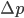 and
and 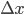 is always greater than a certain minimum value
is always greater than a certain minimum value 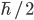 .
.
Perhaps if you are not mathematically inclined, some of the steps above seem like gibberish. But I assure you that they all refer to completely precise mathematical operations, i.e. if somebody handed you a particular mathematical function and said that was the wavefunction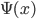 , then you could turn the crank in a completely mechanical fashion to calculate the numbers
, then you could turn the crank in a completely mechanical fashion to calculate the numbers 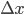 and
and 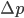 , and all physicists would agree on what those numbers are (assuming they didn't make an arithemtic blunder).
, and all physicists would agree on what those numbers are (assuming they didn't make an arithemtic blunder).
Of course, like everything in QM, the philosophical interpretation is obscure. But whatever interpretation you assign to wavefunctions, the Heisenberg Uncertainty Principle is going to be a true fact about those wavefunctions.
This seems to presuppose that the only kinds of measurements people make in the laboratory are the positions of particles. But there are many other kinds of measurements, e.g. measuring the value of an electric field at a given point (or more precisely, the electric field averaged over some small region of space, since our measuring apparatus always has some finite size). The equations of QFT also say what we should expect to see for these measurements. So I don't see why we should take particles to be more fundamental than fields.
I assume you are aware that these are highly contentious claims, made by some neo-Thomistic philosophers, which many other philosophers would dispute.
I agree that reductionism makes the mistake of thinking that wholes have no idependent existence, except in the sense of being composed of parts. But I think this talk of things only existing "virtually" seems to go too far in the a holistic direction, denying that the parts of the body have any independent existence apart from the whole. I don't see why it can't be true that both the whole and its parts really exist. Even if I grant the Aristotelian premises that only some things exist as "substances", why can't a substance contain another substance?
In any case, it seems clear that my body in fact contains parts, and that (unlike in cheesy Martial Arts movies) Newton's laws of motion seem to apply to those parts, just as much as to any other physical system! I think that we should take this common sense observation into account when constructing a metaphysical system.
Aron Wall,
Thanks for a clearer exposition of the Uncertainty principle than I have ever seen. The question of vague interpretation remains though, after all mathematics.
As Fr Jaki writes:
"An interaction that can not be measured exactly may still take place exactly."
Why assume that if we can not measure p and x exactly, the particle lacks exact values of p and x?
Mactoul,
The difficulty lies in making a specific proposal for how p and x can be simultaneously well defined, which is compatible with everything else we know. These are called "hidden variable theories", and there are various no-go theorems which place significant restrictions on them.
For example the Kochen–Specker theorem says that, in any system described by a Hilbert Space with at least 3 orthogonal states, it is impossible to have all the values of the "operators" (analogues of measurable quantities such as x and p) be simultaneously well defined, in a way which respects all the usual rules of logical implication.
There may well be loopholes in these kinds of theorems, so I don't think one should give up hope entirely. But if it were easy to construct a plausible model of hidden variables, somebody would already have done it!
Still, I am somewhat sympathetic to the idea that it is possible to know more about the world than the Uncertainty Principle would naively allow. For example, in order to make "postdictions" about the past, we need to assume that the universe began in some special low entropy intitial state. (If we naively extrapolate just from our present day direct measurements, without using any such restriction, we would conclude the entropy should increase as we go to the past as well as to the future, leading to absurd conclusions such as e.g. the nonexistence of dinosaurs.) I think this knowledge provides us with more information about the past than would naively be allowed by Uncertainty. (In his original paper on the Uncertainty Principle, Heisenburg says explicitly that it only holds on a forward-going basis, but most people don't think about this sort of thing carefully...)
Mactoul,
Exactness of measurement isn't what drives the Uncertainty principle. It's a consequence of wave-particle duality. The wave function is precisely that: a wave function. According to the more traditional interpretations of quantum mechanics (most notably Copenhagen) this wave function isn't just a mathematical description of how accurately we can measure the position or momentum of a particle--it is the particle. An electron, or proton say, doesn't "look like" a wave or a particle to us until we measure a wave-like or particle-like property in it. But that wave function is still the "thing in itself". Unless I misunderstood his approach (which I may well have), this is why Aron presented the Uncertainty principle to you via Fourier analysis. Any periodic wave function is subject to Fourier analysis, and it turns out that uncertainty principles are a direct mathematical consequence of it. If you describe "position" and "momentum" in a similar manner you can actually derive "uncertainty" relationships for any kind of wave, including sound waves or waves on the ocean. So as long as the "thing in itself" is a wave function of some sort, it must have an associated uncertainty principle between any two conjugate properties (e.g. position-momentum, energy-time, etc.). This is true regardless of how exactly any of those properties can be individually measured. There's a famous principle known as Bell's Theorem which states that no physical theory of "local hidden variables" (the kind we may think are there even if we can't measure them exactly) can ever reproduce all of the predictions of quantum mechanics. It has been tested in experiments and found to be true.
Now that said, it is possible to interpret the wave function differently and construct local hidden variables theories (e.g. the Bohm interpretation of QM) and there are interpretation of QM that do so. If any of these approaches proves to be true, perhaps then we can talk of properties having exact values. But Bell's Theorem requires that in all such approaches quantum effects must be non-local--that is, spread out across space-time in a manner not restricted by the speed of light. Many physicists have a hard time accepting that, which is in large part why the traditional interpretations haven't been more widely rejected. We can't have our cake and eat it too.
It's possible to derive the Uncertainty principle by modeling particles as little "wave packets" and analyzing how such a packet would be knocked around by a photon when observed. It's much easier to derive it like this so that's how it's often introduced in undergraduate courses. It was first taught to me that way in my freshman chemistry class way back when. This is unfortunate because even though it works, it paints a picture of this little billiard ball particle who's location can't be observed by a cue-ball photon without knocking it into the corner pocket. This is the wrong way to think of it. Quantum realities are far more mysterious, and beautiful.
[Aron, if I missed on anything here please correct me. :-) ]
Scott,
My correction is that your comment in square brackets seems to be unnecessary in this case. ;-)
Aron,
Does the Kochen-Specker theorem still leave Bohmian mechanics a viable option? I know that at least in the case of the Bell inequalities, the non-locality of Bohm's theory is what allows it to be consistent. Is this similarly the case with the Kochen-Specker theorem? From your description it would seem that it would not be, since a the position operator, for example, clearly has at least 3 orthogonal states. Thanks!
Matt, is just a single operator---all the information in it commutes---so the Kochen-Specker theorem does not apply to it.
is just a single operator---all the information in it commutes---so the Kochen-Specker theorem does not apply to it.
The Kochen-Specker theorem forbids assigning mutually consistent values to all operators acting on a 3 dimensional Hilbert space. (For a complex Hilbert space "dimension" means complex dimension). The position operator
Thus Bohmian mechanics is not inconsistent. However, it has the somewhat unaesthetic feature that it requires arbitrarily picking a specific basis of the Hilbert space. Bohm picked the position x, but you could equally well pick momentum p. Unfortunately, this arbitrary choice often requires one to break a bunch of symmetries one expects to hold in physics. Also, the most "obvious" basis to pick might change when you reformulate your model---for example, in QFT the most obvious analogue of "position" is the value of a field at a point, which does not correspond to the position of any quantum.
This arbitrariness and breaking of symmetries is, I think, why most physicists dislike Bohm. One could argue that being logically contradictory is a far worse sin than merely breaking some symmetries, but it would be nice to avoid both of these... Those physicists who think the Many Worlds Interpretation makes sense would also criticize Bohm for having all the same structures as MWI, plus more, thus (in their view) violating Occam's razor. I don't think MWI makes sense, but that doesn't mean I'm happy with Bohm either.
Speaking of Bohm and related matters...
A friend (who doesn't have a background in physics) just posted this story to his Facebook page. The model reported therein is based on the use of Bohmian quantal trajectories to derive a quantized Raychaudhuri equation. The approach is news to me and I only had time for a brief review. However I did note that it was originally published in Dec. 2014, and by last summer there was at least one other paper reporting issues with it.
This may be getting off-topic for this post... if so, I can post it elsewhere. But do you know anything about this Aron?
"Exactness of measurement isn't what drives the Uncertainty principle. It's a consequence of wave-particle duality."
And where that come from?
Mactoul,
Where does wave-particle duality come from...? That is the $64 million question! No one knows. There are those who believe quantum mechanics is an outcome of some deeper underlying principle or feature of the universe. But if so, no one has any idea what it is, and in any event that is far from certain. The origin and interpretation of quantum mechanics is one of the central unanswered questions in physics, if not the one. What we do know is that wave-particle duality is at the very foundation of the quantum nature of the universe and the starting point for everything else.
"you could turn the crank in a completely mechanical fashion to calculate the numbers Δx and Δp, and all physicists would agree on what those numbers are "
But what do the numbers Δx and Δp mean? This is where the textbooks get vague.
1) They refer to the spread in the measurements performed on the quantum particles. Of course, to get the spread the measurements need to be performed repeatedly. This case is essentially same with classical statistical mechanics.
2) They refer to the spread in the particle position and momentum PRIOR to the measurement. There is an ontological defect-the particle position and momentum do not exist as unique values. But doesn't this view rests on an equivocation-- if a property can not be measured exactly, then it does not exist exactly?
Consider the thought experiments Einstein proposed to challenge the Uncertainty Principle. All were based on the idea that the particle position and momentum could be measured simultaneously to arbitrary precision. Bohr defeated them showing that it could not be done. But again. doesn't this entire debate rests on the equivocation--logically showing that we could not measure some thing to arbitrary precision, how does that show that that thing does not exist?
Mactoul,
There's nothing vague about the numbers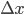 and
and 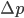 . They're precisely what they're stated to be--the uncertainties inherent in either property prior to their measurement--and that uncertainty can be evaluated precisely via the usual rules of frequentist probability. According to frequentist formalism the measurement of any probability becomes more accurate with increasing sample size. It's entirely meaningful to say I have a 50% chance of returning heads from tossing a "fair" coin before doing so. I know this because although tossing that coin twice won't reliably return a heads and a tails, tossing it 100,000 times will almost certainly return 50,000 of each, and I can conduct such a test prior to tossing the coin again. There's nothing arbitrary about either the prior character of the probability or how I determined it.
. They're precisely what they're stated to be--the uncertainties inherent in either property prior to their measurement--and that uncertainty can be evaluated precisely via the usual rules of frequentist probability. According to frequentist formalism the measurement of any probability becomes more accurate with increasing sample size. It's entirely meaningful to say I have a 50% chance of returning heads from tossing a "fair" coin before doing so. I know this because although tossing that coin twice won't reliably return a heads and a tails, tossing it 100,000 times will almost certainly return 50,000 of each, and I can conduct such a test prior to tossing the coin again. There's nothing arbitrary about either the prior character of the probability or how I determined it.
There's no "ontological defect" involved in quantum uncertainty either. As I pointed out before, the ontological reality--the "thing in itself" so to speak--is a wave function whose very essence exhibits wave/particle duality. Its particle-like "position" and "momentum" are inseparable from its wave-like properties prior to their observation, and each of these properties will manifest themselves in different ways depending on how they're observed.
Consider a single-slit diffraction experiment. If we illuminate a slit with monochromatic light, the target image will display a diffraction pattern resulting from the superposition of the light waves. Now suppose we replace the lamp with a "light gun" that shoots photons one at a time (this can be done). Quantum mechanics tells us that if we shoot a photon "bullet" at the slit, there's an irreducible uncertainty to exactly where it will strike the target. But what's really interesting is that if we repeat this single-shot experiment many times, the resulting pattern of photon "bullet holes" in the target will also display a diffraction pattern just like the lamp! This experiment is no different than tossing 100,000 fair coins to measure a prior probability of 50% heads, yet it results in behavior that's only possible if each photon is subject to wave-like diffraction prior to being observed to strike the target at any unique location. There is no way to account for this in terms of a merely epistemological inability to measure the exact location or momentum of particle "bullets" without resorting to spacio-temporally non-local effects (per Bell's theorem). The thing-in-itself is a wave as well as a particle which according to the usual rules of Fourier analysis must exhibit uncertainty relationships between any canonically conjugate properties it has. It only acquires unique wave-like or particle-like values for those properties when they're observed.
Strange as it may seem, this is the universe God made... in all of its unfathomable mystery and beauty! :-)
Scott,
Numerous people have been asking me about this work, so I see that I will get no rest until I write an article bashing it...
Aron,
By "this work", are you referring to the Bohmian quantal trajectories theories I asked about on 3/04 or the larger uncertainty vs. "hidden variables" discussion of the last couple weeks? Either way, I'm looking forward to your article, and in the meantime I'll do my best to to share whatever I can about both that might be helpfu1! :-)
I was talking about the "Bohmian quantum trajectories" thing which people keep asking me about. Although nobody I actually know in the physics communities I'm a part of takes it seriously, as far as I know.
"the ontological reality--the "thing in itself" so to speak--is a wave function whose very essence exhibits wave/particle duality. "
Well, I don't know if physics is really competent to speak of "thing in itself". Physics necessarily proceeds from certain things as given. But even otherwise, it seems that the wavefunction is a poor candidate of "thing in itself". After all, what is the wave function? Isn't the definition of the wave function that it gives the probability amplitude of a particle being measured in such and such state? So, the particle whose wave function we are discussing, that particle must be the fundamental reality and the wave function being just an attribute of the particle.
Mactoul,
As you say, the wave function does give the probability amplitude of a particle being measured in a particular state. But we need to be very careful with language here. Stating it this way implies prima-facie that the wave function is just an equation we can use to calculate the probabilistic properties of a particle, in the usual sense of that word. This is the wrong way to think about it. The wave function actually describes a reality for which measuring a wave property will return a wave-like value, and measuring a particle property will return a particle-like one. It doesn't do any good to claim that it's just a math equation, and therefore less "real" than something tangible like a tiny billiard ball. In the formalism of QM, the act of observing (measuring) a property is also mathematical. It's given by an operator that transforms the initial wave function into another wave function that is an eigenstate of the initial one--that is, the same function multiplied by a constant--in which the corresponding eigenvalue (the constant) is the property we observe.Take the wave function of an electron for instance. Its wave function will be given by something like,
The act of observing its location, say, is given by an operator--let's call it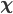 --so that we have,
--so that we have,
where x is the location we observe the "particle" to be at. In this case the eigenstate/eigenvalue associated with the measurement is trivially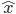 . However, we could just as easily have observed the electron's momentum, for which the operator
. However, we could just as easily have observed the electron's momentum, for which the operator 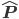 is given by,
is given by,
As can be seen, this time the eigenvalue returned is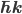 . This is in fact the Debroglie momentum p of the electron, for which there is also a Debroglie wavelength given by,
. This is in fact the Debroglie momentum p of the electron, for which there is also a Debroglie wavelength given by,
Notice that in both cases we start with the same initial wave function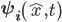 , and end up with a final one,
, and end up with a final one, 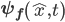 that's just like it up to a constant value. In the first case observing
that's just like it up to a constant value. In the first case observing 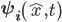 gave us a
gave us a 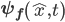 with a particle-like location. In the latter case observing it gave us a
with a particle-like location. In the latter case observing it gave us a 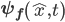 with a momentum and a wavelength. The only difference was in how we chose to observe it. Splitting
with a momentum and a wavelength. The only difference was in how we chose to observe it. Splitting 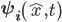 up into a "wave" reality and a "particle" reality is possible--this is what's done in the Debroglie-Bohm approach. But it's arbitrary and unnecessary and in the eyes of most physicists today it creates more problems than it solves. Occam's razor is poised and ready to slice.
up into a "wave" reality and a "particle" reality is possible--this is what's done in the Debroglie-Bohm approach. But it's arbitrary and unnecessary and in the eyes of most physicists today it creates more problems than it solves. Occam's razor is poised and ready to slice.
For what it's worth, interpretations of QM are as messy and problematic to physicists as they seem to everyone else, which is why there are so many different ones, including ones where the wave function is taken as real and ones where it's unreal. All have their strengths and weaknesses, but the most problematic ones are generally those in which one tries to split waves and particles from each in an attempt to preserve what we macroscopic beings consider "common sense". This is why I keep going back to the phrase wave-particle duality. Since it looks like Aron is planning a more complete post that will undoubtedly cover the issues with the Debroglie-Bohm approach far better than I could, for now it's probably best to just leave it at that.
The biologist J. B. S. Haldane once said, "It is my supposition that the Universe in not only queerer than we imagine, is queerer than we can imagine". I'm sure I speak for Aron as well as myself when I say that a big part of why we both pursued physics is that it gives us a glimpse of a universe which is not only fascinating and beautiful, but perhaps mysterious to a point even queerer than we can imagine. In the words of Einstein, we want to know God's thoughts... the rest are details. :-)
[I corrected some bugs in some of the equations above; see below--AW]
Crap... what happened to my double dollar signs...??? :-(
Scott Church,
Is the wave function a physical thing?
Or the "quantum particle" whose wave function it is?
Or is the "quantum particle" identical with its wave function?
Note that the wave aspects are exhibited only under repeated measurements. In the double-slit experiment, a single hit to the screen lits up in a particular place. The diffraction pattern emerges after a number of individual hits to the screen.
Your idea of fundamental ontological status of wave function reminds me of Wheeler's It from Bit.
: “…every it—every particle, every field of force, even the spacetime continuum itself—derives its function, its meaning, its very existence entirely—even if in some contexts indirectly—from the apparatus-elicited answers to yes or no questions, binary choices…bits.”
Would you comment upon It from Bit?
Scott,
The problem wasn't the double dollar signs, it was bugs in the latex expressions. If you use the \left( and \right) commands, it is important that you not put a space or any other symbol in between the command and the parenthesis it acts upon.
Also, in one equation the \left wasn't paired properly with a \right, and in another equation there was a missing { when you began an exponential.
I also took the liberty of replacing some h's with \hbar's as needed. (For those not in the know,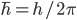 , where h is Planck's original constant, but it turns out that
, where h is Planck's original constant, but it turns out that 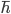 appears in a lot more expressions so physicists mostly use it instead.
appears in a lot more expressions so physicists mostly use it instead.
I keep meaning to add a "sandbox" where people can test equations to their heart's content, or else the ability for people to edit own their comments, but I can't find any worpress plugins which have all the needed functionality. In the meantime, you can of course test your latex on pages like this, but there are differences in which commands are allowed so I can't guarantee it.
Thanks Aron! I actually used the Codecogs page to build/test my equations, but given the Unicode issues I've had with my Notepad I've been putting them into my comments manually instead of copy/pasting. I must've fat-fingered some because they worked fine at Codecogs. Thanks for the hbar change too... I couldn't remember offhand how to do hbar in LaTex and there wasn't an hbar widget at Codecogs. So I just gave up and used "h" because I was in a hurry. In retrospect, "\hbar" seems like a no-brainer... and for that matter, why didn't I just copy the equations from Codecogs instead of my Notepad...? I must've been tired... :-) Regarding a sandbox, WP QuickLaTex for WordPress claims to have a preview feature in Ver. 3.8.4. Have you looked into that one yet?
Mactoul,
I think I'll defer to Aron on It from Bit... To be honest, I could be better versed on the topic, and I imagine he's going to cover it in his current Quantum Mechanics series. I guarantee you he'll do a better job than I could. For now, perhaps the best advice for any of us would be simply to avoid speaking of "wave functions" and "quantum particles" as though they were separate things. Maybe we could coin a term like... "wavarticle" or something... :-) Until someone comes up with a better way to separate the two (which most physicists will tell you hasn't happened yet), it's best to just accept a unified reality that is, in some hard-to-imagine way, both. Best.
Reductionism is a pale outdated model of reality whenever you are trying to analyze a complex nonequillbium system with lots of sensitive, tightly interacting pieces, you need Chaos/complexity theory, check out: http://plato.stanford.edu/entries/chaos/#FreWilCon
Welcome to my blog, kev,
Chaos theory tells us that even if the laws of physics are deterministic (as in classical physics), a tiny change in the initial conditions can (in certain kinds of systems) lead to an enormous difference in what eventually happens. This makes it impossible for human beings to predict what will happen (e.g. the details of the weather for a period of more than about a week.
But this by itself does not refute the reductionist worldview. Because most reductionists don't claim that we scientists could ever actually predict the behavior of a complex system by knowing all its parts. The only claim, as a philosophical matter, that if you know everything about what the parts do, then in principle you would know everything there is to be known about a system.
Mind you, there are lots of good reasons not to be a reductionist anyway, notably its complete inability to explain consciousness as I argued above.
The article you link to is about how in a quantum mechanical world chaos theory might amplify the effects of small quantum fluctuations to larger scales (in the brain) thus (it is claimed by some people) accounting for our free will. There seems to be some physical dispute about whether the brain in fact does this, but probably the more difficult question is the philosophical one of whether one can reasonably attribute such a nondeterministic event, originating at the atomic/molecular level, to the human being taken as a whole.
"small quantum fluctuations to larger scales (in the brain) thus accounting for our free will. "
This is a confusion that ought to be put to rest a long time ago. Quantum indeterminism is irrelevant to the metaphysical notion of free will. Trouble is, people define free will as opposed to determinism, without any qualifications. The notion of determinism is, again, confused in discussions where physics and metaphysics intersect, because determinism is differently defined in the two disciplines.
Physics is the study of laws of necessity that govern inanimate bodies. It does not extend to the laws that govern animate bodies and rational bodies.
Determinism, in the older sense, is the idea that things do not happen without (sufficient) reason.
However, the 20C usage relates to the precise configuration of physical systems.
Quantum mechanics, is deterministic under the older usage but (possibly) non-deterministic under the modern usage.
Free will is a capacity of rational animals who move by deliberation. The special movements of rational animals are beyond the province of physics, classical, quantum mechanical or whatsoever.
You say: "Quantum Mechanics appears (at least for all practical purposes, leaving aside Many Worlds and other bizarre interpretations) to be nondeterministic. The outcome of a given experiment can only be predicted statistically, in terms of probabilities."
But on the Firewalls comment you implied that an objective collapse view has major problems. I am not sure how this makes sense.
When it comes to interpretations of quantum theory, you basically have four broad camps: those that make no ontologically significant pronouncements (e.g. The Copenhagen interpretation), those that reject the reality of super positions (hidden variable theories), those that accept the reality of super positions but deny that a transition to a single state ever occurs (the "many worlds" interpretation, aka the "look-guys-I-proved-that-Schrodinger's-cat-can't-trip-over-its-own-dead-body-so-we-don't-need-that-cludgy-collapse-thing-anymore!" interpretation), and those that accept both the reality of the superposition and the transition to a single state (objective collapse interpretations). Number one makes no statement about determinism, and numbers two and three are both explicitly deterministic. Which leaves option four: objective collapse. But you don't seem fond of option four. So what am I missing?
Hi again Aron,
Just for some clarification:
In your post about consciousness, I think I read that you said that neuroscientists have found that quantum mechanical effects were not observed in the brain (something you said in response to one of the commenters presenting a paper from Penrose I think?), but you did mention that you think indeterminism plays a role in our behavior. You also argued that a sort of interactionist dualism where the conservations laws are violated every time the "soul" interacts with the brain is implausible but not as implausible as naturalists claim.
I know one cognitive scientist who tries to argue for libertarian free will from a reductionistic framework. I never read his book but apparently he traces his indeterminism to how the neurochemistry in the brain is sensitive to neuronal spikes that can be traced to the behavior of a single ion that obeys quantum mechanical laws. Would you say that you'd prefer a non-reductive physicalist approach to free will (where we are our brains but indeterminism allows for LFW, although its exact mechanisms are unknown) or a dualist view where it doesn't matter if indeterminism affects our brain because the immaterial soul can interact with it anyway?
also, I wanted to clarify what you meant about the quantum events affecting our behavior but that the actual computing done by our brains are macroscopic hence obey the Newtonian laws.
Pingback: Free Will, Physics, and God (Q+A Response) | Veritas Christo et Ecclesiae
Sorry in advance to resurrect an ancient thread, but I only discovered your blog a few days ago and couldn't resist binge reading it! I also wasn't sure whether to post this in this thread or in the "Free Will" thread, but I'm picking this one because the post has a good statement of what has always bothered me about reconciling omniscience with free will—the accidental necessity of the past: "There is a fact of the matter about whether I chose to marry my wife St. Nicole, and an observer can know that fact with certainty, but that does not make the decision retroactively unfree. I cannot now change this decision, but my past self could have done otherwise."
As it happens, I do believe God is timeless for the usual scriptural and other reasons, but I've never been able to figure out how that solves the dilemma. The usual statement of the problem depends on the intuition that while the past could have been otherwise, it is now not open to us to take any action that would change it, and combines it with the the fact that if something is necessary, and it entails something else, that something else is necessary as well. (As discussed earlier in the thread—if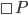 and
and 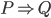 then
then  . That's certainly true of logical necessity, and it seems plausible that it would be true of the "accidental" necessity the past now has.) If you buy both those things and a few other hard-to-dispute premises, it seems like you have a problem:
. That's certainly true of logical necessity, and it seems plausible that it would be true of the "accidental" necessity the past now has.) If you buy both those things and a few other hard-to-dispute premises, it seems like you have a problem:
What about if God is timeless? Well, I personally find it quite hard to have strong intuitions about a timeless being, but almost everyone who thinks that God is timeless still believes that God can act in time. If so, you can simply restate the problem in terms of God intervening to make a prediction in time. ("God created a tablet yesterday that stated that you will answer the telephone tomorrow at 9 am, etc.")
What about the proposed solution in the "Does God Need a Brain" post—if there's a problem with "God knows X," wouldn't there be the same problem with "X is true"? I agree with this, in the sense that it seems like some propositions like "X is true" are not entirely about the past, so they don't share in the accidental necessity of the past. (For example, "It is true that yesterday's meeting was the first or four monthly meetings" is partly about the past but partly about the future, so we don't have the same intuition that it's not now open to us to affect its truth.) Maybe the same thing is true about facts like "God knows X"—if people from William of Ockham to Alvin Plantinga think so, who am I to reject it as absurd? But it's hard for me to see why "God knows X" is different from other propositions we think of as accidentally necessary. And when you add in interventions by God, even less seems accidental necessary: For example, a colony of ants moved into Paul's backyard, and it's God's will that the colony be preserved. But Paul chooses to mow the lawn tomorrow, God would have seen to it that the colony didn't move in. So it seems like whether the ant colony would have moved in depends on whether Paul chooses to mow the lawn tomorrow. And similarly, it's possible that there are things that you could do in the future such that, if you do them, you would not have married St. Nicole. And all that seems hard to swallow.
I guess if I had to accept one of these implausible propositions, it would be the last one—maybe the class of accidentally necessary propositions is much smaller than I would have though. But I'm not entirely happy with it, and would love any thoughts on how to make this more palatable.
Raghav K,
It seems to me that there are at least two ways that this tension can be resolved. One solution is to say that God’s being omnipotence means that He knows everything that it is logically possible to know. Since it is not logically possible to know what a free agent will decide to do, God cannot know what Bill will decide to do tomorrow. This does not conflict with His being omnipotent, and may not rule out His having a very good idea of what Bill is likely to do tomorrow.
The second way to resolve the tension is via the well known concept of “Middle Knowledge” of Molina and da Fonseca.
Given an array of possible worlds, God knows what all individuals will freely choose in every possible circumstance. If placed in one set of circumstances, God knows what Bill would freely choose and placed in another set of circumstances, God knows what Bill would freely choose.
Hi James,
I agree that the first option resolves the issue, though at the cost of jettisoning a good deal of the Christian tradition. Some may be willing to pay that price, but I'm reluctant to contradict such a great cloud of witnesses. In any event, as discussed in the Peter van Inwagen paper I linked above, it's hard to reconcile Open Theism of this sort with some of the promises that God has made—that at lease some people will be saved, for example. But since the theological and philosophical merits of Open Theism have been extensively discussed on this blog, you can think of my question as being directed at those who (like Aron) reject Open Theism but want to maintain that libertarian free will exists.
I also have objections to Molinism (again, like Aron and others in this thread), but for present purposes will just note that Molinism doesn't provide a reason to deny any of the premises in the argument excerpted above. So the Molinist also needs to have some other counterargument to that fatalist argument.
Hi Raghav,
“I agree that the first option resolves the issue, though at the cost of jettisoning a good deal of the Christian tradition. Some may be willing to pay that price, but I'm reluctant to contradict such a great cloud of witnesses. “
I’m not sure that acceptance of this viewpoint involves jettisoning the tradition. It seems to me that traditionally it has always been understood that God’s being able to do everything that it is logically possible to is the way we should understand His being omnipotent. For example, this is arguably implicit in Hebrews 6:18 where it says that “God did this so that, by two unchangeable things in which it is impossible for God to lie, we who have fled to take hold of the hope set before us may be greatly encouraged.” This suggests that God was not viewed by St Paul as being able to do the logically impossible. Furthermore, many medieval theologians always understood God’s omnipotence in this way. So I see the view I outlined more as a drawing out of an old tradition, not a break with it.
“I also have objections to Molinism (again, like Aron and others in this thread), but for present purposes will just note that Molinism doesn't provide a reason to deny any of the premises in the argument excerpted above. So the Molinist also needs to have some other counterargument to that fatalist argument.”
For the argument to work a certain notion of “knowledge” is required. If one understands knowledge probabilistically, then God could have known the relevant counterfactual with a high probability. In other words I am claiming that a credence can be knowledge.
Raghav,
Welcome to my blog!
[There is no need to apologize for commenting on an old thread. I actually prefer that to people starting off-topic conversations in new threads.]
First of all, I agree God is timeless, so the argument as you've stated it isn't valid (as you yourself point out).
But I think I would also question the validity of the concept of "now-necessary". I am not sure there's any particular reason to admit this as a primitive modal concept. Things can be relatively necessary, in the sense that they are beyond the power of an individual agent at a particular time to change, but this is a highly context-dependent property, and I see no reason to think that supernatural intervention (such as prophecies of the future) might not allow finite being's choices to have retrocausal influence, even though this is normally physically impossible.
As for how time-travel paradoxes are avoided in cases of prophesy, I'm not sure but presumably it helps that God is omnipotent so he can ensure that history is self-consistent.
Alternatively, there is the concept of the absolute necessary, which is beyond the power of any entity, even God, to change. But I think this category is best thought of as a timeless one. Once you put in any temporal stipulations about when it can be changed, you are no longer talking about absolute necessity but only relative necessity (or perhaps, absolute necessity of a conditional statement e.g. conditional on you committing adultery, it is not within the power of God to make it so you are a virgin.)
JamesH,
I'm not a Molinist because of the Grounding Objection. I don't think the concept of "middle knowledge" is coherent, becuase if God does not create an entity then I think there is no fact of the matter about what they would do.
To back up St. Raghav's point, the reason why it contradicts tradition is not simply because of the definition of omnipotence. If it were merely an abstract argument, along the lines "God can do this because he can do anything", then I agree it would be open for somebody to argue that the thing in question is actually instrinsically impossible.
The trouble is that in the Bible, God explicitly claims to know the future, and demonstrates this knowledge by making predictions about the future many times (even about things that are seemingly the outcome of human free will, like St. Peter's denial of Christ, or Josiah's desecration of Jeroboam's altar). For example God's ability to predict the future is a major theme in Isaiah, (see chapters 41-48).
For more about this, see my post on Foreknowledge.
Thanks for the response, Aron. As I said, I think I end up in pretty much the same place—that things in the past might be different depending on what I choose to do in the future—but I'm not entirely happy about it. (Note that I don't think the relation necessarily has to be a causal one, as your reference to retrocausation suggests.)
I'm guessing this should read, "I see no reason to think that supernatural intervention (such as prophecies of the future) might not allow a finite being's choices to have retrocausal influence," right? If so, I agree with you that what I above called the "accidental" necessity of the past isn't a type of logical necessity. It simply expresses the following intuition, the description of which I borrow from the van Inwagen paper linked above: "in every possible continuation of the present state of affairs, the same propositions about the ‘present past’ (the past before the present moment) are true as are true in the present state of affairs." Or, as you put it above, "I cannot now change this decision, but my past self could have done otherwise." I personally find that intuition pretty strong, and while I feel compelled to abandon it for the reasons sketched out above, I would love to find a way of salvaging it.
(And I don't think an atheist confronts the problem quite as strongly, despite the argument in your Fundamental Reality VII post, since I don't think that propositions like "It was true yesterday that Raghav will tell a lie on June 15, 2031" or "It is true that yesterday's meeting was the first or four monthly meetings" are entirely about the past, so they don't share as strongly in the intuition I sketched out in the previous paragraph.)
The usual way I've seen Open Theists address this is to suggest that fewer decisions are free than we ordinarily think. (That's the option that seems to be endorsed by van Inwagen with respect to St Peter and Judas in the essay above, and I know it's also Dean Zimmerman's view.) For example, if I were (God forbid) to steal someone's wallet tomorrow, perhaps that decision isn't free, but is rather the unfree result of a character that I built up through other free choices I made in my past; similarly, perhaps it was already "baked in" to St Peter's psychological makeup at the time Christ made his prediction that under such-and-such a circumstance he would thrice deny Our Lord. Personally, it seems unlikely to me that (say) the penitent thief had no free choices open to him that would forfeit his place in paradise following the promise in Lk 23:43, but I don't know that there's anything in scripture that definitively excludes that possibility.
Raghav,
Yes, there was a missing "not". Good catch! I fixed it in my original comment, so people won't be confused reading it.
You may also be interested in this comment of mine if you haven't read it already. I was reminded of it while tracking down the following quote by St. David Hunt, which I reproduce here: