In a previous post, I argued that falsifiability is not the be-all and end-all of Science. There are valid scientific beliefs that are not falsifiable.
However, there is something to the idea that beliefs should be falsifiable. One way to make this precise is to use Bayes' Theorem. This is a rule which says how to update your probabilities when you get some new evidence E. It says that your belief in some idea X should be proportional to your prior probability (how strongly you believed in before the evidence), times the likelihood of having measured the new evidence given X. (You also have to divide by the probability of having measured the new evidence, but this is the same no matter what X is, so it doesn't affect the ratio of odds between two competing hypotheses X and Y. It's just needed to get the probabilities to add up to 1). As an equation:
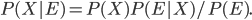
For example, suppose you believe there is a 1/50 chance that there exists a hypothetical Bozo particle (I just made that up right now). And suppose you perform an experiment which has a 50% chance of detecting the Bozo if it exists. Just for simplicity in this example let's suppose there are no false positives: if you happen to see the Bozo, it leaves a trail in your particle detector which can't be faked.
There are two possible outcomes: you see the Bozo or you don't. In order to see the Bozo, it needs to (a) exist and (b) deign to appear, so you have a 1% chance of seeing it. In that case, the probability that the Bozo increases to 1.
On the other hand, you have a .99 chance of not seeing the Bozo. In that case, your probabilty ratio goes from 49:1 to 98:1 since the Bozo exists possibilities just got halved. This corresponds to a 1/99 probability that the Bozo exists.
On average, your final probability is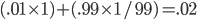 
. Miraculously, this is exactly the same as the intitial probability 1/50 of the Bozo existing! Or maybe it isn't so much of a miracle after all. On reflection, it's pretty obvious that this had to happen. If you could somehow know in advance that performing an experiment would tend to increase (or decrease) your belief in the Bozo, that would mean you that just knowing that the experiment has been done (without looking at the result) should increase or decrease your probability. That would be weird. So really, it had to be the same.
We call this property of probabilities Reflection, because it says that if you imagine yourself reflecting on a future experiment and thinking about the possible outcomes, your probabilities shouldn't change as a result.
Now Reflection has an interesting consquence. Since on average your probabilities remain the same, if an experiment has some chance of increasing your confidence in some hypothesis X, it must necessarily also have some chance of decreasing your confidence in X. And vice versa. They have to be in perfect balance.
This means, you can show that it is impossible for an observation to confirm a hypothesis, unless it also had some chance of disconfirming it. VERY ROUGHLY SPEAKING, we could translate this as saying that you can't consider a theory to be confirmed unless it could have been falsified by the data (but wasn't).
Even so, there are a number of important caveats. In some situations in which we can and should believe things which are, in various senses, unfalsifiable. This occurs either because (a) The Reflection principle doesn't rule them out, or (b) the Reflection principle has an exception and doesn't apply. Here are all the important caveats I can think of:
- It could be that the probability of a proposition X is already high (or even certain) before doing any experiments at all. In other words, we know some things to be true a priori. For example, logical or mathematical results (such as 2+2 = 4) can be proven with certainty without using experiments. Similarly, some philosophical beliefs (e.g. our belief that regularities in Nature suggest a similar underlying cause) are probably things that we need to believe a priori before doing any experiments at all.
.
Propositions like these need not be falsifiable. This does not conflict with Reflection, because that only applies when you need to increase the probability that something is true using new evidence. But these propositions start out with high probability.
. - It could be that a proposition has no reasonable chance of being falsified by any future experiment, because all the relevant data has already been collected, and it is unlikely that we will get much more relevant data. Some historical propositions might fall into this category, since History involves unrepeatable events. Such propositions would be prospectively unfalsifiable, but it would still be true that they could have been falsified. This is sufficient for them to have been confirmed with high probability.
. - Suppose that we call a proposition verified if its probability is raised to nearly 1, and falsified if its probability is lowered to nearly 0. Then it can sometimes happen that a hypothesis can be verifiable but not falsifiable. The Bozo experiment above is actually an example of this. There is no outcome of the experiment which totally rules out the Bozo, but there is an outcome which verifies it with certainty (*).
.
This doesn't contradict Reflection. The reason is that Reflection tells us that you can't verify a hypothesis without some chance of lowering its probability. But it doesn't say that the probability has to be lowered all the way to 0. In the Bozo case, we balanced a small chance of a large probability increase against a large chance of a smaller probability decrease.
.
The Ring Hypothesis was another example of this effect. We have verified the existence of a planet with a ring. Had we looked at our solar system and not seen a planet with a ring, this would indeed have made the Ring Hypothesis less likely. But not necessarily very much less likely. Certainly not enough to consider the Ring Hypothesis falsified.
. - Suppose that, if X were false, you wouldn't exist. Then merely by knowing that you exist, you know that X is true. But X is unfalsifiable, because if it were false you wouldn't be around to know it.
.
For example, no living creature could ever falsify the hypothesis that the universe permits life. Even though it didn't have to be true. Nor could you (in this life) ever know that you just lost a game of Russian Roulette.
.
This type of situation is an exception to the Reflection principle. The arguments for Reflection assume that you exist both before and after the experiment. (You can also construct counterexamples to Reflection involving amnesia, or other such funny business.)
To conclude, these are four types of reasonable beliefs which cannot be falsified. It is a separate question to what extent these types of exceptions tend to come up in "Science" as an academic enterprise (as opposed to other fields). But I don't see any good reason why these exceptions can't pop up in Science.
(*) Footnote: Some fictitious person (let's call her Georgina) might say that the Bozo is still falsifiable since nothing stops us from doing the experiment over and over again, until the Bozo is either detected or made extremely improbable. Hence, Georgina would argue, the Bozo IS falsifiable.
My answer to Georgina is that it actually depends on the situation. Maybe the Bozo experiment can only be done once. Maybe (since I'm making this story up, I can say whatever I want) the Bozo can only be detected coming from a particular type of Supernova, and it will be millions of years before the next one. More realistically, maybe the Bozo is detected using its imprint on the Cosmic Microwave Background, and the phenomenon of Cosmic Variance means that you can't repeat the experiment (since there is only one observable universe, and you can't ask for a new universe). More realistically still, maybe the experiment costs 100 billion dollars and Congress can't be persuaded to fund it more than once.
Georgina might not like the last example very much, since she might say that all she cares about is that the Bozo is in principle falsifiable. Perhaps as a holdover from logical positivism, the Georginas of this world often talk as though this makes some kind of profound metaphysical difference. But it's not clear to me why we should care about falsifiability in principle. The only thing that really helps us is falsifiability in fact.
If a critical experiment testing the Bozo will not be performed until next year, for purposes of deciding what to believe now, we should behave in exactly the same way as if the experiment could never be done. Experiments can't matter until we do them.
Hi Aron! I've been reading this blog on and off for a while, and since you hit on a topic I really like (falsifiability and science), I figured it was time to comment. While I have a few comments/questions, let me focus on the two biggest ones:
1. It had never occurred to me to use Bayes' Theorem in this way to describe the process of conducting experiments, and it seems pretty cool. However, there's one key feature that I don't understand: how does one quantify the probability of a claim about the universe being true? In fact, I don't even mean this in practice; I don't see how it it even makes sense in principle. For instance, you claim that there is a 1/50 chance that the Bozo particle exists. Does that mean that out of 50 possible universes, only one can contain the Bozo particle? Does it mean that out of 50 competing theories, only one posits the existence of this particle? Something else? Without a definition of this probability, it seems to me that the Bayesian analysis is meaningless.
2. This may be (in fact, probably is) a semantic issue, but what do you mean by "science"? In my mind, a scientific theory is broadly defined by two key features: it is (i) a prescription for predicting nontrivial outcomes of experiments or observations, with (ii) a domain of applicability in which it purports to be valid. Note that by a "nontrivial outcome", I mean an outcome that is not tautologically true (e.g. the statement "if I drop an apple it will either fall or not fall" is not a theory, because the statement "the apple falls or it doesn't fall" is trivial). Then by construction, these features imply that a theory must be falsifiable, since an experiment performed in its domain of applicability could in principle disagree with its prediction. Any claim that does not contain these two ingredients I would not call a theory, whether it is verifiable or not (e.g. the Ring Hypothesis). Of course with this definition the question "Does science need to be falsifiable?" is trivial, so I wonder what your definition is.
Dear Sebastian,
Welcome to my blog! Thanks for your questions.
1. None of the above. Since the number of "possible universes" and/or "possible theories" is infinite, we can't simply count them to find out what fraction contains a Bozo. (And we shouldn't do that in any case, since there is really only one universe, so far as I know, and there are plenty of terrible theories that shouldn't have equal weight with the good theories.) No, when I say that the probability is 1/50, what I really mean is that your subjective expectation is that, given everything you already know, and prior to doing the experiment, you think the odds are 1 in 50 you'll see it. In other words, it's a measure of your subjective psychological state. (Or, if you prefer, the psychological state of an idealized rational agent who knows everything you know.) If I already know the results of the experiment, my probability to think Bozos exist will be different from yours.
As to how you go about quantifying your psychological state with a specific number, except in some special cases where symmetry tells you an exact answer, you have to "eyeball it". Just like when you decide how high a painting should go on the wall to look best aesthetically with the other stuff---it feels wrong when it's too high and when it's too low, and you pick the place that seems best. If this seems incorrigably subjective, well, I'm afraid that deciding how plausible different ideas are is just part of life.
There's a nice dialogue about what this all means here: http://math.ucr.edu/home/baez/bayes.html
2. I have a (fallible, and partly unconscious, but real) prescription for predicting how my wife will respond to various stimuli, administered in the domain of dependence of our relationship. Does that make my marriage into a Science? If not, perhaps we need a better definition of Science.
Also, does your definition of Science allow for the predictions to be probabilistic? If not, it won't include QM. If so, the predictions might not be falsifiable for the reasons I describe in the main post.
I'd rather define Science from the "bottom up", by first identifying the fields of study which are commonly considered to be Sciences (in the modern sense of the word) such as Physics, Chemistry, Biology, etc. and then asking what distinguishes them from other things. That's what I tried to do with my Pillars of Science series. I expect that any definition which is as simple as yours will end up including many things which are not commonly regarded as Sciences. I'd rather try to identify general characteristics of Science than look for a strict black-and-white definition. My parents are linguists, you see, and they drilled into my head that concepts are defined by their centers rather than their boundaries. (A beanbag chair may be a chair by certain definitions, but it's not going to be what pops into your head if I say "chair".)
Even under your definition, a scientific theory might not be falsifiable (by us) if it predicts "experimental" outcomes only in a domain of dependence which we don't have access to. For example, many ideas about Quantum Gravity could be tested if we could probe distance scales as small as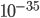
meters, but this is absolutely impossible with current (or any reasonably forseeable future) technology. So does that make Quantum Gravity scientific, or not? I think it's best to get comfortable with ambiguity, and say, "Yes in one sense, no in another". It is, however, unambiguously true that Physics departments pay people like me to think about it...
Thanks for the replies!
1. Having briefly looked at the document you linked, as well as the Wikipedia article on Bayes' theorem and Bayesian probability, I think I understand why I was confused by your original claim. I had always interpreted probability from the frequentist point of view, wherein I thought of probabilities as assigned to possible outcomes of an event. You, on the other hand, appear to be using the Bayesian interpretation, where probabilities refer to beliefs.
I should still do some reading on the topic, but let me just say that while I think I could eventually be convinced to adopt the objectivist view of Bayesian probability, I really don't like the subjectivisit view - at least, not for formal reasoning. It's certainly true that we colloquially use probabilities to refer to subjective beliefs all the time (e.g. "I think it's 99.99% likely that there is no Santa Claus", etc.), but I find it hard to believe that such vague notions can actually be useful in anything other than casual conversation. But, since I'm just starting to learn about this now, please feel free to educate me!
2. It looks like we're taking different approaches here - I like an axiomatic approach, where I take my definitions and axioms as given and go from there. For instance, if I just stuck by my definition, then I'd say yes, you do have a scientific theory for predicting how your wife will behave in certain contexts (in fact, I do mean this somewhat seriously - in a sense, psychology just consists of developing and testing models to describe and predict people's behavior, and I'd consider that an application of the scientific method).
You, on the other hand, are taking something like a top-down approach - you're trying to find some unifying characteristics of what most people would think of as "science." I have nothing against this sort of approach to things - in fact, I think it can yield some very interesting insight. But I think the insight it yields is sociological insight - it tells us about the mindset of a society at some point in time. I don't think it really provides any information about the idea in question.
As an example, I took a philosophy of art course in undergrad, and we spent the entire first half of the semester trying to come up with a definition of art. It felt a little like this:
"Consider definition M for art. Clearly, it includes pieces of art X and Y. But it doesn't include piece of art Z, and some people think Z should be considered art, so definition M is no good. Next, consider definition N for art. It includes pieces of art X, Y, and Z, so it's better than M. But actually some people don't think Y should be considered art, so definition N is no good either. Next, consider..."
and so on. This was both fun and infuriating at the same time: fun, because this sort of approach illuminates the way people's perception of art changed over time; infuriating, because (a) it was doomed to fail, since obviously there's no consensus among the public (or art experts) for what should and shouldn't be considered art, and (b) it prevented us from ever just picking a definition and rolling with it.
Thinking about science in your top-down approach is great for illuminating how much the notion of "science" has changed over human history. But just as "science" was radically different two thousand years ago from what it is today, in another two thousand years it may change just as dramatically. So whatever notion of "science" you come up with in this way will be very impermanent and tied to the era (and culture) in which it was developed.
Dear Sebastian,
Somewhat surprisingly, it turns out that subjectivist Bayesian methods actually are useful in doing real science, notwithstanding the squishiness of choosing your prior probabilities. Normally the "objective" methods are more or less equivalent to Bayesianism with a particular choice of prior (and when frequentist methods are not so equivalent, normally you can prove that they are objectively wrong!) Performing a Bayesian analysis makes this choice explicit, so that you can examine whether or not you believe in it. In other words, if you don't do Bayes, you aren't avoiding the arbitrariness in your choice of prior. Instead, you are swallowing the arbitrariness whole without examining it.
For example, suppose you are doing an experiment where you are considering whether a certain physical effect exists or not. You aren't sure whether it's there at all, and if it is there, you aren't sure how big it is. A reasonable thing to do in this case might be to pick a prior which is a weighted average of A) a delta function on the parameter being 0, and B) a continuous distribution over nonzero values of the parameter. Or suppose you are measuring the mass squared of the lightest neutrino. If you get a slightly negative answer (and some early experiments did...) it would be foolish to conclude that the neutrino is probably a tachyon. Bayesian statistics can tell you the correct mean value of the neutrino mass, conditional on the assumption that it is (with very high prior probability) positive.
Besides there's this: http://xkcd.com/1132/
As for things like Art, I think that maybe the real moral of your Art class is that it's better to describe art than to define it. You've probably noticed that when you look up words in the dictionary, there's words they can define, like bracelet, "a piece of jewelry worn on the wrist", and then there's words that nobody can really define so they just start describing them, like frog, "any of various largely aquatic leaping anuran amphibians (as ranids) that have slender bodies with smooth moist skin and strong long hind legs with webbed feet". (Definitions are taken from Miriam-Webster.)
In any case, as annoying as the exercise might be, I think it is important to calibrate definitions of common words by comparing them to the common usage of the word. Otherwise people might get confused. I don't think it's necessarily important for the word ``Art'' to cover everything a depraved modern artist might be tempted to do in order to offend people---in fact, it might really be better for all of us if we agreed the word doesn't cover such things! But it's worth checking whether it gets things right which are clearly Art or not Art, leaving out the weird edge cases.
I guess I do think that Science IS a sociological phemoneon, associated with a particular type of community. At one level, it's just a refinement of the same observational skills which people have been using for thousands of years. But somehow we've refined it to the point where things have really taken off. And we want a word to describe this aspect. On the other hand, when people start putting Science-with-a-capital-S on a pedestal and venerating it as the source of all knowledge, then it's time to remind ourselves that it's really just people looking at the world and thinking about it. Which people do in a variety of ways, many of which don't (and shouldn't) happen in Science departments.
It's up to us to decide whether the word should be defined broadly or narrowly. The confusions usually arise when people slip back and forth between the two illicitly.
Aron, your last link is broken (trailing right-parenthesis).
[Fixed it. Thanks---AW]