Another question from St. Paul, the reader from New Zealand:
I hope that you are well and that you are having fun with your work. I see that you posted our email exchange on your blog, it was a great answer and much appreciated.
I actually have another question I would like to ask, (although I realise that you may well be planning on writing about it already) but as always I completely understand if you don't have the time!
I've been reading about the recent detection of gravitational waves and how they confirm the theory of inflation. What I have found interesting is that there have been quite a few articles reporting that most models of inflation imply the existence of a multiverse, with quotes from Alan Guth, etc. I realise that the term "multiverse" can be used for several quite different situations, but they seem to be referring to one with variation of the laws of physics, meaning the anthropic principle can be invoked.
I was wondering what you make of this new discovery and what your take on the idea of the multiverse is? I have always felt that the fine-tuning argument was a helpful pointer to God, so I am curious about the implications of confirming inflation (although the existence of multiple universes certainly doesn't rule Him out).
Thank you for your time,
Paul
A quick explanation concerning "fine-tuning" and the "multiverse". Fine-tuning refers to the observation that the fundamental constants of Nature seem to take special values which appear to be necessary to the existence of life. The fine-tuning argument is a theistic argument which claims that this is good evidence for the existence of God.
One common atheistic retort is to say that maybe there are lots and lots of universes—with different laws of physics in each universe—and that any observers would therefore have to live in the universes which permit life. This idea is a called the multiverse.
This may sound like crazy science fiction thinking, but I actually think it is the most plausible naturalistic response, given what we now know about physics. Although there is no really good reason to believe in the multiverse, it seems much more plausible then any of the attempts to construct physical mechanisms to account for this fine-tuning.
However, it is not really clear to me that the multiverse is the sort of thing that ought to count as an explanation for fine-tuning. In some moods it seems to me like cheating. Science normally works by postulating theories to fit the observed data, not by postulating (new and unobservable) data to make the theories we have seem less weird.
In fact, there are in fact some serious controversies as to how to properly do Bayesian reasoning in the context of a multiverse. Pretty much all viewpoints lead to some horrendous paradoxes. Since the proper way to do probabilistic reasoning in this context is unclear, it is also unclear to what extent the multiverse would be an explanation for fine-tuning. But this is a complicated question I don't have time to go into right now.
Instead, Paul asks the different question of to what extent the multiverse is supported by real, actual Science. In particular, the very recent results from last March about inflation. For those of you who have been living under a rock, there was a recently announced experimental result in cosmology. The BICEP2 experiment claims to have seen the gravitational waves resulting from inflation, a very early period in our universe's history where the size of the universe expanded at an extremely quick, exponential pace.
[Update: the BICEP2 results have since been discredited.]
I wrote to Paul roughly as follows:
Most models of inflation predict "eternal inflation", meaning not that there wasn't a beginning, but that in some regions of the universe, inflation continues forever towards the future.
In order to have a multiverse of the sort that might be conceivably relevant to fine-tuning, you need to meet two criteria: (a) a mechanism for producing gazillions of different universes (at least 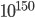 without supersymmetry, or
without supersymmetry, or 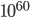 with supersymmetry), and (b) in these different universes, there are an equally large number of different effective parameters describing the low energy physics in each of the universes.
with supersymmetry), and (b) in these different universes, there are an equally large number of different effective parameters describing the low energy physics in each of the universes.
Eternal inflation is conducive to (a) insofar as it would result in widely separated regions which can never causally communicate with each other even at the speed of light. But it does not by itself do anything to meet condition (b). The best argument for (b) is probably string theory, which seems to have gazillions of different types of metastable vacua, but there is currently no successful experimental predictions for string theory. (String theory does seem to imply the existence of gravity, but that's more of a retrodiction, and isn't unique to string theory...)

Is there any sense in which the multiverse could be considered a timeless, infinite entity that would eliminate the need for God as a beginning to the universe?
The "multiverse" is just a bunch of evolving universes, so it's not timeless. If by a multiverse one effectively means one big universe with a lot of regions, then most of the same arguments that I discussed in the series "Did the Universe Begin" would also apply to a multiverse.
Aron, I've got a quick question as well. It seems to me that as you said, within the context of the standard model eternal inflation by itself does nothing to give us child universes with wildly different laws of physics. For any given bubble universe appearing from some excited inflaton potential state I don't see how reheating alone could lead to any differences in how underlying symmetries (like say, the Higgs mechanism, or electroweak symmetry) actually break leading to differing parameters. It seems to me that from the standpoint of fine tuning, the multiverse idea requires the string vacua of M-theory to have any teeth. To my understanding those vacua are defined by the underlying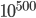 calabi yau manifold configurations possible within the framework.
calabi yau manifold configurations possible within the framework.
If so, are these vacua actually metastable in the sense that any of the possible topologies could, for lack of better terms, "freeze out" of an underlying 11-dimensional "foam" as the larger universe cools, or do they merely reflect a lack of knowledge of the underlying one that constrains string states? Cosmologists these days talk about eternal inflation and a multiverse with gazillions of different sets of physical laws as though they're synonymous. But it seems to me that this is only possible if M-theory is true specifically in the former sense.
Am I missing anything?
Hmmm... I thought I did the LaTex per your instructions and copied out of Notepad, but it didn't seem to render right. Could it be an ascii/unicode thing? Guess I'm still getting used to this. :-)
[Fixed. The problem was somehow you used ∧ rather than the standard ASCII carat ^ ---AW]
Scott,
That's right, the Standard Model by itself does not allow child universes with "different laws of physics", so to speak. It has got only one vacuum state. In order to get enough vacua to potentially explain fine-tuning, you need a significantly more complicated theory. For example, string theory (I'm not sure I know of any other plausible examples, but that may just be due to our lack of knowledge about quantum gravity.)
I'm not an expert on string theory model building, but I gather that the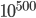 number doesn't come from the number of Calabi-Yau manifolds alone. (Calabi-Yau manifolds are the ways of compactifying 6 dimensions of the 10 dimensional string theory, in a way which preserves supersymmetry.) While no one knows exactly how many Calabi-Yau's there are (it might even be infinite), currently there are only about 30,000 known-to-be-distinct choices. To get a number like
number doesn't come from the number of Calabi-Yau manifolds alone. (Calabi-Yau manifolds are the ways of compactifying 6 dimensions of the 10 dimensional string theory, in a way which preserves supersymmetry.) While no one knows exactly how many Calabi-Yau's there are (it might even be infinite), currently there are only about 30,000 known-to-be-distinct choices. To get a number like 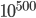 , you need to include "flux compactifications" in which various higher dimensional versions of electromagnetism have different amounts of electric flux wrapped around various cycles. I think you also need to include various types of higher dimensional membranes to build realistic models. To break supersymmetry you need to include "antibranes" which have the opposite electric charge from the other branes; it is controversial which of these models are unstable, but at least some of them are probably okay (assuming string theory is true to begin with). This is the KKLT scenario.
, you need to include "flux compactifications" in which various higher dimensional versions of electromagnetism have different amounts of electric flux wrapped around various cycles. I think you also need to include various types of higher dimensional membranes to build realistic models. To break supersymmetry you need to include "antibranes" which have the opposite electric charge from the other branes; it is controversial which of these models are unstable, but at least some of them are probably okay (assuming string theory is true to begin with). This is the KKLT scenario.
A metastable state is one which lasts for a while and then eventually decays (as opposed to an unstable state, which decays right away, or a stable state which lasts forever in the absence of an external force). Normally in QM, one expects that there will always be a tiny probability to decay into a lower energy state, unless the state has the lowest possible energy given its conserved quantities. If there are an enormous number of possible vacua, one expects that most of them will be metastable, that is there will be a small probability to decay. (If our own vacuum is metastable, the halflife must be at least billions of years, or one would expect it to have already decayed to something else.)
I think you are using the term "metastable" in a confusing way in your question. Normally when people talk about a vacuum being metastable, they are referring to the probability of decay FROM the vacuum, whereas you seem to be interested in the probability of decay TO our vacuum state. Let me rephrase your question as "What is the probability that a vacuum like ours would form from some particular simple initial 11 dimensional spacetime foam state, by some reasonable spacetime history?" (supposing the universe began in such a state). I don't think anybody knows how to calculate the answers to questions like this...
On the other hand, I think most string theorists generally expect (it isn't proven, but it's plausible, see this paper for an argument) that any inflating vacuum will have some nonzero probability to decay to any other particular inflating vacuum state. If so, and if eternal inflation occurs, then with probability 1 there will exist a bubble of any particular kind we like SOMEWHERE in the multiverse. To what extent this counts as a prediction / explanation of what we see is a very deep and difficult philosophical question.
Aron, thanks! As usual, this is just what I needed. And yes, you formulated my question better than I did. What I had in mind was decay TO one or more vacuum states during post-inflation reheating, and whether that would result in child universes with physics just like ours or different physics. It always seemed to me that given eternal inflation, string/M-theory is required to make the latter possible. And thanks for clarifying the nature of those vacua as well. I was under the mistaken impression that within the formalism, Calabi-Yau manifold topology alone determined the landscape. I've been meaning to read the original KKLT paper but haven't got around to it yet. I'll read the other one you linked as well.
Speaking of string/M-theory, I just finished Peter Woit's book Not Even Wrong and thoroughly enjoyed it. I've been dropping in at his blog too (when I'm not here :-) ). He gets a lot of traffic from string theorists and some of them are seriously pissed at him for his stance on M-theory and the multiverse. He gets regular visits from some heavyweights too... Lee Smolin drops in from time to time, and so does Susskind. Spending time there really gives one a feel for the controversy surrounding all this... at times it sounds almost like a religious war. To me that's revealing, if for no other reason because it provides an antidote to all the big-name folks that treats M-theory and the multiverse like they're self-evidently a done deal. In the wake of the Carroll-Craig debate, I'm beginning to see why Carroll gets so testy when folks bring up the subject of falsifiability.
And you confirmed my LaTex Fail theory as well. I usually write my posts in Notepad and copy/paste them. For development-related reasons I have my Notepad configured for Unicode rather than ASCII, and I've been wondering if that wasn't my problem. Sounds like it was.
Blessings!
Scott,
You're welcome.
BTW, I think the standard eternal inflationary multiverse picture is that there are different possible vacua during inflation, with some probabilities to tunnel between them, but that once you start exiting inflation (i.e. during reheating) it is already pretty much determined which kind of universe you will end up in... so "reheating" isn't the relevant time period for universe selection. (Here I'm assuming that inflation ends by some field slowly rolling down its potential, and not by suddenly tunneling into a noninflationary state. This "slow roll" assumption is needed to get cosmologies that look like ours.)
Only part of the inflationary potential is eternally inflating (and there are some models of inflation that are not eternal).
Hi, Mister Wall.
I Was reading some of your posts about fine tuning, BGV theorem and the multiverse, but one of the things that are bothering me a lot is the idea of the multiverse.
I’m a bit skeptical about the multiverse hypothesis. Why the multiverse would create (or allow) the existence of dysfunctional universes (Life-Prohibiting) and functional universes like this one at the same time? How could that be possible? Is it not paradoxical? I mean, as far as I know, one of the ways to know that there’s a multiverse (I don’t remember where I read it) is by observing the gravitational influence of other universes over ours. Am I right? What would that imply? That implies that the multiverse is influenced by laws of nature and physical constants that allow the gravitational influence of other universes over ours and, by taking it as a reference, that implies that the multiverse is fine tuned for its own existence. How could the multiverse's generating mechanism of universes would create dysfunctional universes, while this mechanism is influenced by fine-tuned constants and inmutable laws of nature? How those dysfunctional universes could be independent from the multiverse but, at the same time, still being influenced by the multiverse? it’s like expecting to see a galaxy in our universe with different laws and constants and, as far as I know, the laws of nature and physical constants never evolve, they’re inmutable, the “dysfunctional” galaxies are technically fine tuned because they’re under the same laws as our planet and galaxy are. Why the multiverse must be different?
Or, in a better picture and accepting that multiverse seems to vary its constants or its own laws, How is possible that our universe seems not to be affected by these inconstant constants or mutable laws, and still being part of it at same time? It doesn’t seem to be rational, and it’s like expecting to see a balloon full of water with tiny gelatin spheres and squeeze (or freeze) the ballon and expect to see that the spheres are not affected by the pressure or the temperature changes and so on. Could be more rational to think that the multiverse only allows -forever- the existence of functional universes because it is fine-tuned for it? Could the multiverse be a fine-tuned for fine-tuned universes for intelligent life? and if not, what could be the naturalistic explanation for that kind of multiverse that varies its own constants and laws? the only one I can think about it is that the multiverse is conscious, it’s self aware, and the multiverse knows what it wants. Kinda supernaturalistic, or something else that violates rationality or the logic of science.
The only thing that can be rational to believe that all the universes are fine tuned and they only vary in quantity of matter or energy. Just imagine a box with pots full of soil in it, every pot represent the universes and the box is the multiverse. The box determines what happen with the pots and the pots are basically made of the same material and full with the same type of soil, the only thing that makes them different is the quantity of soil. Some of them will be completely full whiles others just would have one particle of soil. I think thats more rational and plausible than the multiverse that allows functional and dysfunctional universes at the same time.
I'm not a physicist, but think that the more probable (plausible and best) hypothesis is the one that is the least paradoxical, unless that's my opinion. What do you think?
P.D. excuse my english, and sorry if my comment would look a little bit aggressive or something like that, but these ideas were flying around my head all this year. I'll wait for your response patiently.
Mr. Maolong,
No worries about the style of your comment, that is fine. However, I think whoever told you about the multiverse has gotten some things seriously confused.
The word multiverse can mean different things to different people, but as far as I know, nobody has proposed a multiverse model where you could observe the things in other universes by their gravitational effects on ordinary matter! Rather, in most multiverse scenarios it is impossible for us to interact with the other universes. This is not good from the perspective of creating an interesting science fiction story, but it does prevent the multiverse from having the conceptual problems you described.
In the most respectable multiverse model, which is based on string theory and eternal inflation (which are both speculative, but not unmotivated, theoretical proposals for how the world might work), the different "universes" consist of different regions of spacetime which are so far away that they cannot communicate by means of any signals travelling at or below the speed of light. Because the region between the different "bubble universes" is rapidly expanding, in fact the different universes will never be able to communicate with each other, by gravity or any other interaction. Thus it is impossible to test the idea of this kind of multiverse directly. However one might be able to test some of the ideas which support it.
If the string theory multiverse idea is correct, the deepest laws of Nature (string theory) would be in fact the same everywhere. That would not change. However, there are many different ways for the fields in string theory to be arranged, and these different arrangements can give rise to effective laws of physics describing the appearences of low energy phenomena in in different regions of the universe. Similar to how physics in water seems very different from physics in the middle of the sun, even though both regions are described by the same effective laws of physics. But there would only be some specific sets of effective laws that are allowed by string theory. So that is the idea.
The reason why our effective laws of particle physics don't seem to change, would be because the amount of energy it would take to move our universe from one kind of "vacuum" to another kind of "vacuum" is enormously large. Our vacuum would be "metastable"---lasting a very long time---but in principle a large fluctuation could cause it to transmute into a different ground state. As long as the half life of our vacuum is significantly longer than the current age of the universe, there is no conflict with observation.
While I do believe that the laws of physics---whatever they turn out to be---were designed by a supernatural Creator, I don't think the physical multiverse itself would have any kind of consciousness. One could imagine a multiverse in which all the universes are fine-tuned, but the string theory multiverse would probably not be an example of this---most of the configurations people can think of would not be suitable for life, but a very tiny fraction might be OK.
I am not saying that the multiverse idea is necessarily correct, just trying to explain it in more detail.
Ok... thank you very much. I'm still betting for fine-tuned multiverse, but thanks for your response, very informative. And don't get me wrong, I'm a Deist... that multiverse scenario was so problematic to me in a philosophical way because I read the comments of some deist (not here, of course) thinking almost the same about the multiverse, because our perspective of the universe is the immutability, as much here as much in the multiverse
Thank you very much, I wish a merry christmas and a happy new year.
If you believe in fine-tuning, why not a fine-tuned single universe? (Just curious.)
Because I like the idea of a multiverse, maybe in other universes I'm the creature I would love to be, something like a Na'vi creature or an anthropomorphized tiger... or maybe there are dragons as pets... you know, that kind of sci-fi stuffs. I can dream, right? But I do not believe in that kind of multiverse that generates universes with different laws or different constants... seems to be really paradoxical to me, but I want to wait and see.
The problem with the fine-tuning argument is that it makes no distinction between stochastic events and events with agency. Probability calculations are a necessary but insufficient condition.
I notice that when Bill Craig debates Sean Carroll he said fine tuning was due to necessity, chance or design. Bill ruled out necessity as an explanation of fine tune by appealing to string theory. If you have inflation and string theory both true it seems likely you can solve the fine tuning problem. It seems to me there is more evidence for inflation than for string theory. However what if inflation is true and string theory is false? Then the multiverse may not be such a good response against the FTA but then one wouldn't be in such a strong position to rule out necessity either.
David,
Your comment is too cryptic for me to get anything useful out of it. But one point is that Bayesians use probability to refer to a person's personal subjective degree of belief. It doesn't matter whether an event is "stochastic" or involves "agency", if you are uncertain about the outcome then you can describe your uncertainty using probabilities, and then update when you get new evidence.
howie,
I agree that St. Craig's move there was somewhat questionable, since taken as a whole String Theory would be somewhat bad for the Fine Tuning Argument. Even without eternal inflation, there is the issue that String Theory does not seem to have any continuously adjustable constants (in that sense, the ultimate fundamental laws are physically necessary, within the framework of String Theory). The seemingly different constants in all those different vacua are really just different configurations of the fields. This does not necessarily rule out fine tuning althogether, but it means that any such tuning would have to involve initial conditions---selecting the right vacuum state---rather than tuning of the deepest laws of physics (once you know the laws of physics are described by String Theory in the first place, that is!).
(In fact his division of the possibilties into "physical necessity, chance, or design" is a little odd. For example, a multiverse fits rather oddly into the "chance" category.)
However, if as you suggest string theory is false, then I don't thnk that postulating "physical necessity", without anything more, is a good explanation for why the universe supports life. Saying "the universe had to be just the way it is" still doesn't explain why the way that is necessary coincides with the way that supports life. See my response to Explanation #4 in my fine tuning talk.
I never got around to making a post on the fine tuning issues in the Carroll-Craig debate, but eventually I should, since I think both participants made some pretty serious errors.
I just discovered this site a few days ago. Very inticing discussions!
As for this one, I've always found the fine-tuning argument peculiar. As far as I'm aware, there's no observation or experiment to suggest physical constants are items that can be 'tuned' or changed with time. They're called constants for a reason unless I've missed something. Is there anything (that doesn't depend on non-confirmable ideas like strings) to suggest physical constants can change with time?
Hello Andrew,
As physicists use it, the term "fine-tuning" has nothing to do with physical constants varying over time. The term refers only to the fact that many such constants happen to fall within extremely narrow ranges consistent with the existence of life and intelligent observers like us. The analogy is drawn from the way a radio can only pick up broadcasted content when it's set to very specific frequencies. Beyond that, no reference is being made to any physical constant actually being "dialed in" to life-permitting values in any sense.
Best.
Thanks for the reply, Scott!
That's what I've come to understand too. It's why it surprises me that it's actually an argument that apologists take seriously.
I don't think it is just apologists who take fine tuning seriously, Aron and Scott both do and have done posts about it. Google search for "aron wall explanations for fine tuning" to see some slides from a
presentation he did. As far as I know both Aron and Scott take it seriously. Hopefully one of them can explain why it is a good argument for God.
I agree with your first statement, Chris. Several physicists also take it seriously, which surprises me all the same. I should've stated that too.
But my point was that from everything I've seen, the spirit of the fine-tuning argument hinges on the "what if" question. Sometimes physicists ask this question, only to illicit wonder in non-scientists as a means of attracting them to science. But it is not always something that should be accepted as a real possibility. Neil Tyson demonstrates this on an episode of Cosmos where he describes black holes as worm holes that could take us to exciting places in our universe or other universes. Non-physicists might be lead to believe this is something that most physicists accept if they miss Tyson's very brief, initial statement before the wild journey that "you're entering uncharted scientific territory." I think to some degree, this is what has happened with the fine-tuning argument. Except for some reason, many physicists fell into the same trap and brought non-physicists with them. In proposing that constants are 'fine'-tuned, nearly everyone has taken the extraordinary leap of faith in assuming they are 'tuned' or even tunable! It seems to me that such a premise requires some reason to even expect it as a possibility. But there doesn't appear to be any. This of course doesn't refute the fine-tuning argument, but it seems to me that it does illegitimize it until we learn the necessary information... that constants are items that can 'take on' values. Sure, they 'take on' values when we discover them, but that doesn't mean they had any value before discovery. Aron seems to recognize this reasoning in the presentation that Chris pointed out. On Slide 36 he states odds of entropy if randomly selected, followed by the statement, "there's no particular reason why the state should be random."
Basically with a very crude analogy the fine-tuning argument seems like asking, what if 10 were actually 11? At present, the basis of the argument seems like another fruitless question. Physicists entertaining the question is a surprise to me, but apologists taking it even further and using it as evidence to support another extraordinary claim is in some ways even more perplexing.
I don't really have time to explain why I personally find fine tuning compelling (finals are approaching for me) but perhaps Aron and/or Scott can explain why they think it is a good argument in technical terms. I would point out though, that the entropy example you listed was in the presentation listed under "Other (less convincing) kinds of fine-tuning" so that implies the other (earlier mentioned) cases are more convincing and not subject to the same criticism. http://www.michaelgstrauss.com/2017/07/is-fine-tuning-fallacy.html
As for the number example, I can't say that I find that even remotely close to what is being argued. Ten can't possibly be something other than itself, there are no models or argument that suggest a specific quantity could have been another quantity, that is a meaningless question. However, we do have mathematically consistent models that allow for universes with different law structures and widely different constants. Aron's example earlier, I quote, "That's right, the Standard Model by itself does not allow child universes with "different laws of physics", so to speak. It has got only one vacuum state. In order to get enough vacua to potentially explain fine-tuning, you need a significantly more complicated theory. For example, string theory (I'm not sure I know of any other plausible examples, but that may just be due to our lack of knowledge about quantum gravity.)" So the point here is that the question fine tuning asks is not like asking "why is 10 not 11?" which is meaningless because it is metaphysically and definitionally impossible for a necessary number to have been something else. Instead, the fine tuning argument notices that we could have had a universe with different constants/initial conditions, so why do we have one that falls within the life permitting range? Simply put, we have good reason to think that our universe could have been different (from the starting initial conditions), but there is no reason at all to think that numbers could have different identities. We could use the sound we make for 11 to mean the quantity 10, but the quantity ten doesn't change its nature, there is no physical procedure or model that explains how that could happen; unlike fine tuning where we can easily construct models that would not be life permitting. Finally, here is a technical article from Luke Barnes that might be helpful in explaining why fine tuning is not a trivial "what if" question - https://arxiv.org/abs/1707.03965
Hello Andrew,
Sorry for the delay in responding! The last couple weeks have been pretty busy for me, and stressful. Regarding your last, there are a few things that probably should be clarified.
First, as I alluded to before, the strength of the fine-tuning argument has nothing to do with the "tunability" of any fundamental physical constant. The mystery before us is that there are a number of such constants that can theoretically assume a vast range of possible values, yet by the most striking of coincidences just happen to fall within vanishingly small ranges consistent with the existence of reflective, self-aware observers like us... capable of wonder, gratitude, and worship. If anything, it would be easier to account for these coincidences if some degree of variability made it possible to "tune them in." A metaphorical radio with no tuning dial just makes this bio-friendly miracle that much more astounding!
Nor does this argument hinge on any "what if" question. These constants are quite real, their values have been robustly determined, and amidst a vast sea of theoretically valid possibilities, they do, in fact, assume astonishingly specific bio-friendly values... and for virtually no known reason. In this respect, Christopher is correct. The comparison of 10 to 11 isn't valid here. The mathematics of real, cardinal number lines constrains those numbers to their assigned values. But the physical constants in question here are not constrained to anything like their observed values by any physics known or on the horizon. While it is possible, as of this writing there isn't a shred of evidence to suggest that they are so constrained, or even can be.
Notice that this miracle will remain true even if we do discover that they are constrained by a deeper theory with no tuning dials. Such a theory would be even more sophisticated, subtle, and miraculously specific than anything we've imagined so far, which would only deepen the same bedrock dilemma: Of all the infinite forms the laws of physics could have assumed, the universe reflects one of the vanishingly tiny few that not only yields what Eugene Wigner called, "the unreasonable effectiveness of mathematics," but makes us possible as well. Whence this unreasonably effective mathematical universe so perfectly suited to creatures like us? There are no "what if's" here Andrew. This miracle is as concrete, and baffling as it gets! :-)
And there are only three possible ways to account for it. The first, of course, is sheer, dumb luck. Coincidences do happen after all. Maybe we just got lucky and drew one quadrillion royal flushes from a quadrillion-shoe deck of cards. This is possible of course, but for the obvious reasons few if any physicists take it seriously. Which leaves us with two remaining possibilities;
1) A vast blunderbuss of universes. Keep drawing universe cards from nature's deck for however long it takes until you draw a hand with observers like us, infinitely if necessary.
2) Design. Accept that the universe was purposely, and even lovingly crafted, at least in part with the intent of producing reflective, self-aware observers.
Needless to say, right out of the gate die-hard atheists will consider the latter option anathema. So the only real option open to them is some sort of multiverse that keeps drawing universe cards until they get what they're after. This is where "what if" questions might enter, Stage Right. However, it isn't enough to simply postulate such a multiverse. If this framework is to have any theoretical teeth, there must be a viable physical mechanism that can produce one. Furthermore, this mechanism must allow not only for child universes but ones whose fundamental physical constants can vary widely enough that given enough tries, our existence would eventually turn up. And if this multiverse is not past-eternal (which is likely), this will have to be a likely outcome in the time available since its beginning. For more on all this, I would also recommend the paper of Luke Barnes' that Christopher linked, as well as his book with Geraint Lewis, A Fortunate Universe.
The closest anyone has gotten to this is the string landscape/eternal inflation multiverse. I don't know how many of them would admit it, and it isn't my place to put words in their mouths. But given what to them will be the dismaying prospect of 2), I suspect this is why multiverse theories are as popular as they are today with many atheist physicists and thinkers, despite their lack of solid theoretical grounding and any possibility of empirical testability.
"Of all the infinite forms the laws of physics could have assumed"
For instance?
Do the physicists know a single different form that a particular law, such as Coulomb's law could have assumed? Note that we are talking about a whole consistent set of laws that are needed to produce a consistent universe.
That was going to be my question too, Mactoul. You say there are a number of physical constants that can theoretically assume a vast sea of values. Mactoul points out you make the same claim about physical laws. What is the justification for this?
Theoretical physics is full of models that are perfectly consistent, and even useful, but don't describe the universe we live in. Some examples off the top of my head: multiple metrics in GR (e.g. the Godel metric), various quantum field theories (e.g. phi-cubed theory), heck for that matter, Newtonian mechanics (which is a good approximation in most cases but not the full story of what's going on - given how long it was the dominant paradigm in physics, this should make it the paradigm case of a model that's internally consistent but doesn't really describe the universe we live in). It is not too difficult to come up with laws of physics that are different from the ones we actually find in our universe. Given that we have a variety of perfectly consistent alternatives to the universe we actually experience, it doesn't seem unreasonable to ask, "Why these laws, rather than some other ones?" It's not like these are the only self-consistent set of laws, and physics doesn't say a priori which set of laws are right - we can only tell which is right by observation.
Likewise with physical constants - there's no reason why, say, the fine-structure constant *has* to be 1/137, rather than, say, 1/138, or 1, or 42, at least not as far as theory is concerned - that value is just measured experimentally and inputted into the theory. Theory has nothing to say about what value the fine-structure constant is - as far as theory is concerned, the value could be pretty much anything. You can give it pretty much any value you like on paper and the theory is still consistent.
I think this is what is meant when talking about how the constants 'could have been different'. It's just noticing that theory is silent on what values the constants take, and *as far as theory is concerned*, their values could be anything. It's not saying that there's a physical mechanism by which constants change, nor is it necessarily putting forward a metaphysical view where these constants are 'tunable'. All it's saying is that there is no theoretical reason for the constants to take one value over any other.
Again, it doesn't seem unreasonable to then ask, "If my theory is still consistent regardless what value I give these constants, why do they turn out to have these values rather than any other ones?"
It gets more interesting when you include the realisation that life (or complex chemistry, or whatever) is only possible if those constants fall within a certain narrow range.
I don't think this commits you to the view that there is a metaphorical tuning dial or anything like that - I think even if the constants couldn't have been different from the values they have, it would still be a legitimate question to ask, "Why these values rather than other ones?" Compare: plenty of mathematical truths couldn't have been otherwise. But it still makes sense to ask why that's the case - why this theorem rather than that one, etc.? That's the whole point of proofs, after all.
Likewise, we can still quite legitimately ask, "Why these values, and why in this life-permitting range, rather than some other values?", even if, in the final analysis, it were to turn out that they couldn't have had any other values after all.
Andrew and Mactoul,
Andrew2 took the words right out of my mouth [or fingers :-) ]. Physics is full of models that are internally consistent and useful, but very different than the universe we live in. There are two respects in which this is true, and he gives good examples of both. Here are some further thoughts and examples of my own.
First, there's the allowed variability in fundamental physical constants. Case in point, consider the Newtonian gravitational constant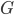 , and the cosmological constant
, and the cosmological constant 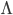 . Their observed values are;
. Their observed values are;
Neither of these values can be derived from any first principles, and virtually every known law of physics allows for them to be many orders of magnitude larger or smaller. They are fundamental because there is one, and only one way to obtain them, and that is to measure them. And yet, if either were even slightly different, we wouldn't be here. Depending on how one does the accounting, there are at least 26 of these constants, and per other estimates, 31. Like the above, all could assume vastly different values than they do without being in conflict with any known or foreseeable physics. They just are what they are. BTW, Mactoul, Coulomb's Law doesn't escape this either. It depends on the fine structure constant Andrew2 mentioned, which as he correctly pointed out, isn't constrained to the observed value of 1/137 in any known way. Yet if it were significantly different, Coulomb's Law would preclude our existence as well.
Second, there's no reason why the laws themselves have to be what we observe. Over the last century, countless physical theories have been proposed and tested. Again, Andrew2 gave some good examples. Others examples would be "fifth force" theories, alternate cosmologies, or inflationary models and inflaton candidates. These days, there are almost as many of the latter as there are salaried cosmologists. All but a handful have gone the way of the world, not because of any internal inconsistencies that precluded them from being possible, but simply because they failed observational tests. If we had a legitimate reason to believe the laws of physics couldn't be any different than they are, there wouldn't be a need for universities and research institutes to fund experimental physics. ;-)
For another perspective, here's something else to consider. While we're a long ways from a viable "theory of everything" and string theory (or more properly, M-theory) has no shortage of issues, Aron and many other physicists believe that nature will ultimately lend itself to some sort of "stringy" description. But whether or not that turns out to be the case, at the very least, the M-theory framework provides an internally consistent theoretical framework that certainly could be true in principle. And it's particularly telling that it allows for a mind-numbingly large "landscape" of false vacua. At least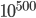 such vacua are thought to be possible, and according to some recent estimates, there may be as many as
such vacua are thought to be possible, and according to some recent estimates, there may be as many as 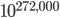 (see this paper co-authored by a friend of Aron's). [For some perspective on how large these numbers are, consider that the number of subatomic particles in the entire visible universe, 27+ billion light years in diameter, is thought to be on the order of
(see this paper co-authored by a friend of Aron's). [For some perspective on how large these numbers are, consider that the number of subatomic particles in the entire visible universe, 27+ billion light years in diameter, is thought to be on the order of 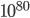 or so.] Each of these vacua would result in vastly different particles, forces, and laws of physics. We don't know how many of them are stable or have exact theoretical solutions yet, but the fact of the matter is that every one of them is certainly possible. If the universe proves to be unlike any of them it'll be because its laws just don't happen to take that form... not because they couldn't have in principle.
or so.] Each of these vacua would result in vastly different particles, forces, and laws of physics. We don't know how many of them are stable or have exact theoretical solutions yet, but the fact of the matter is that every one of them is certainly possible. If the universe proves to be unlike any of them it'll be because its laws just don't happen to take that form... not because they couldn't have in principle.
The bottom line is this... There is an infinite number of internally consistent, and entirely possible forms the laws of physics could have taken. And no matter how you do the accounting, the astronomical majority of them preclude any possibility of reflective, self-aware observers who can take it all in and give thanks. That is the mystery of fine-tuning. Indeed, one of the biggest reasons for the popularity of the multiverse Aron discusses in this post is that for atheist and agnostic physicists, it's the only option they have that offers any hope at all of being able to account for fine-tuning without being forced to acknowledge a Creator... and even it doesn't rule one out.
Best.
And then there are the digital physics proponents (who claim that the universe is a cellular automaton or something similar). That’s a whole different can of worms.
There seems to be some competing claims here so I'll try to parse them out.
First, there's this statement:
"Again, it doesn't seem unreasonable to then ask, 'If my theory is still consistent regardless what value I give these constants, why do they turn out to have these values rather than any other ones?'"
The error here is that the theory (whatever theory) regards the constant in the theory as a constant. This doesn't seem to be in dispute, right? Our ignorance of the one true value of the constant doesn't mean all possible values before discovery are actually real. The universe has been doing what it's doing before we know the value of the constant. This same problem can be seen in the Barnes paper that was mentioned a few times when he discusses the cavendish experiment. The surprise to me is when people still assume the hypothetical possibilities were real possibilities even after the actual value is discovered.
To me, it's like arguing that even though we now know the earth is round, it could have just as well have ended up flat because we used to think that it was flat. It seems like "tuners" (I just coined that term, haha) give these possibilities equal credence when one is not possible in reality.
Now, there is a separate claim here that our universe, under governing rules, is able to 'take on' values of the constants in our theories. But as I see it, we do not yet have a confirmed or confirmable theory of our early universe (or pre-universe for the designers here) that gives it the ability/mechanism to 'take on' imagined possibilities of constants in theories.
Scott, you said there are no 'ifs' in the tuning argument. Yet you go right back to the ifs in your last statement. The Barnes paper presents ifs numerous times. You're all demonstrating the If question is the heart of the tuning argument. And it seems to be a really big If, because constants are constants by observation and by theory and still, no one has presented any reasonable justification to warrant asking such an If.
Hi Andrew,
Let me (hopefully) clear things up. I don't think anyone has said that all values of physical constants are equally real until measured. Certainly I haven't said that, as that strikes me as speculative at best and ludicrous at worst. As I said above, it's still reasonable to ask why certain things are the case, even if they couldn't have been otherwise.
Your analogy with a flat vs. round earth could be instructive. I think we agree that it wouldn't be too clever to claim that the earth could just as well have been flat as round, just because people used to think one rather than the other (I note as an aside that actually belief in a flat earth was not terribly prevalent historically, but that's by the by). However, we can still ask, "Why is it round, rather than flat, or hemispherical, or banana-shaped, or whatever?" Asking why things are the way they are, rather than some other way, is a huge part of the scientific project. And I don't have to really believe that the earth could have been banana-shaped in order to ask that question.
Likewise, asking why, say, the fine-structure constant is 1/137 rather than, say, 42, doesn't entail belief that there's some way by which it could have been 42 instead of 1/137.
Here's an analogy which might help. The surface area of a sphere is given by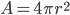 . Now, we can just accept that, or we can ask why that formula, rather than a different one? Why not
. Now, we can just accept that, or we can ask why that formula, rather than a different one? Why not 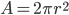 ? Now the first equation couldn't be different - there's no way that the surface area could be given by the second one. But you can still ask why is it the first formula, rather than the second. (And to answer that question, we'd go through such and such a proof (say, involving surfaces of revolution) and be able to explain why the first formula and not the second.) I can still ask that question, even if I don't believe things could have been otherwise. And indeed, asking that question can help you understand why things are the way they in a deeper way, because you understand why alternative 'possibilities' aren't real possibilities at all.
? Now the first equation couldn't be different - there's no way that the surface area could be given by the second one. But you can still ask why is it the first formula, rather than the second. (And to answer that question, we'd go through such and such a proof (say, involving surfaces of revolution) and be able to explain why the first formula and not the second.) I can still ask that question, even if I don't believe things could have been otherwise. And indeed, asking that question can help you understand why things are the way they in a deeper way, because you understand why alternative 'possibilities' aren't real possibilities at all.
Hopefully this should make it a bit clearer that you don't have to believe things could have been different in order to ask why they are one way rather than a different way.
I'm going to briefly address one bit of terminology which I think could be a sticking point - when physicists talk about changing the values of some constant, they don't mean, say, that the fine-structure constant used to be 1/137 and then changes to 42. Rather, they're asking, what if it had never ever been 1/137? What if it had always been 42 instead? What would the universe have been like then?
You can call this an exercise in speculation if you want - fine, I probably agree with you. Think of it as science fiction. But again, as with most science fiction, you can ask why it's science fiction rather than science fact. Why aren't there hoverboards? Why can't I time travel? And why isn't the fine-structure 42, but 1/137 instead?
Best,
Also Andrew.
Hello Andrew,
As Andrew2 said, no one is claiming that all values of any fundamental constant are actually real before we discover one of them to be. What's being said is that our current physics renders them all possible, which leaves us with the question of why they're found to have these values rather than those ones. "Tuners" [yes, clever term! :-) ] give equal credence to all possible values because the laws of physics do. In the complete absence of any shred of evidence to the contrary, no one value is any more likely than any other. Nor are these constants "[constant] by theory." They are only because we observe them to be. Countless experiments have searched for variation in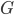 ,
, 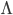 ,
,  , and other fundamental constants, and none has ever been observed. Furthermore, if some of them had varied appreciably over the history of the universe there would be unmistakable consequences for the large-scale structure of the universe, and these aren't observed either. No theoretical constraint requires any of this. It's just what experiments and observations have confirmed.
, and other fundamental constants, and none has ever been observed. Furthermore, if some of them had varied appreciably over the history of the universe there would be unmistakable consequences for the large-scale structure of the universe, and these aren't observed either. No theoretical constraint requires any of this. It's just what experiments and observations have confirmed.
The round vs. flat earth analogy is irrelevant here. That question arose long before the rise of modern science for reasons that had nothing whatsoever to do with physics, and physics isn't ambiguous about the shape of the earth in any way that would raise a fine-tuning question. In fact, in the absence of correspondingly large angular momentums, Newtonian gravitation requires planetary and larger bodies to be near spherical in shape, and it's no surprise that planets, stars, black holes, and other such astronomical bodies are.
There appears to be some misunderstanding of the "if" questions here. When I said there were no "ifs" in the tuning argument, I was referring only to the fact that fundamental physical constants do exist, have narrowly life-friendly values, and are, in fact, not constrained in any way whatsoever by the laws of physics. Given these facts, it's entirely reasonable to ask why they are found to have values that fall within very narrow life-friendly ranges when virtually nothing we know about the universe requires them to, and what the universe would be like if they didn't. This is no different than asking why the guy next door married Lisa instead of Kathy, and how his life would've been different if he'd married Kathy instead. One can meaningfully explore that question and draw some conclusions without presuming that he's a polygamist, or that he had a gun to his head and had no choice in the matter. :-)
Best.
Scott,
Your analogy is not representative of what we're discussing here. Assuming we observe Lisa and Kathy are real people, then marrying either of them were real possibilities. That we can observe both of them and the act of marriage, actually does make it a different question. We do not have such a luxury concerning our universe. I would alter your analogy to make it Lisa vs Wonder Woman. We could of course ask why the guy next door chose to marry Lisa instead of Wonder Woman (nerds like me would really wonder), but you see where this is headed. We're imaginative creatures, and I'm not discounting that it may be a fun question with fun answers, but in terms of informing reality, we have to be disciplined in our inquiry and potential answers. The answer to the question here is Lisa is the real "possibility" so that's what we observe.
Concerning constants, sure we can ask the question, why this value instead of that. But the answer is, because that's what we observe. My point remains that the answer really is trivial until we observe that there actually were alternate possibilities. We don't run wild with our laws of Physics. There may be no constraints on constants in the laws themselves, but we don't just rely on the laws. We are also guided by observation. Consider Newton's gravitational law (or even Einstein's replacement). There are no constraints in the equations restricting negative masses or even mass values with imaginary numbers. But we never observe such things, so there's no a priori reason to go and search for them or even regard them as real possibilities because we simply do not observe them.
So yes, I see the fine-tuning argument as an exercise in speculation. But an unwarranted one because of our observation. Until we observe constants can actually be or could actually have been other values, I think it prudent to avoid running wild with the speculation. Just like marrying Wonder Woman, it's a fun question to ask, but the question and answers are not informing us on reality.
- Andrew
Hi Andrew,
I do not find your response all that convincing. Consider this claim you make: 'Concerning constants, sure we can ask the question, why this value instead of that. But the answer is, because that's what we observe.' I think you might be missing the point. Consider this analogy: We can ask why is the sky blue, rather than green. But if I answer, 'because that is what we observe', then I'll have missed the point of the question. The question is asking for an explanation for the sky being blue (say, due to Rayleigh scattering). Likewise, just responding, 'because that is what we observe' doesn't really answer the question - we're looking for an *explanation* for why the constants have the values they do, and just saying, 'because that's what we observe' doesn't really cut the mustard.
Onto your concerns about possibilities:
Perhaps it's useful to think of different types of possibility. On one level you've got physical possibility - that's whatever is possible according to the laws of physics. But there are other levels of possibility. A different level would be logical possibility. If something isn't a logical contradiction, then it is logically possible. Here are a couple of examples, to provide some intuition: a married bachelor is not a logical possibility, because that would be a contradiction in terms. However, a perfect circle is a logical possibility - there's nothing contradictory about a perfect circle. But a perfect circle most likely isn't physically possible - no matter how precisely you draw it, it will never be perfect, because the atoms that make up your drawing will ensure it has a finite resolution - at some level of magnification, it will cease to be a perfect circle. So a perfect circle could be an example of something that is logically possible, but not physically possible.
Clearly, everything that is physically possible is also logically possible. But not everything that is logically possible is physically possible.
Now, barring certain speculative theories like string theory, the fundamental constants we're interested in don't change. So you could claim that it is not physically possible, given our current understanding of the laws of physics, for the constants to change.
However, there is nothing logically contradictory about supposing that the fundamental constants have different values to the ones we measure. So it is at least logically possible for the fundamental constants to have different values.
I do not think proponents of the fine-tuning argument are necessarily talking about physical possibility when they talk about it being possible for the constants to be different. I think it more likely they're talking about logical possibility.
Of course, there's an alternative possibility. Philosophers will sometimes talk about metaphysical possibility, which seems to be something in between logical and physical possibility. The notion of metaphysical possibility seems a little woolly, but I think, again we can gain some intuition about it with an example. There is nothing logically contradictory about saying that some event E happened with no cause - it is logically possible for an event to happen without a cause. However, you might claim it is metaphysically impossible for E to happen without a cause - in any world that happens to exist, E will always have a cause, regardless of what laws of physics obtain. I think this should provide some intuitive sense of what people might mean by metaphysical possibility.
It seems fairly clear to me that 'tuners' might be referring to metaphysical possibility, when they talk about constants possibly having different values.
So, I don't think tuners are claiming that it is physically possible for the constants to have different values. It seems much more likely they're claiming it is logically and/or metaphysically possible for them to be different.
P.S. I'll point out in advance that you don't have to agree with the claim that every event E has a cause - I'm just using it illustrate what sorts of ideas might be candidates for metaphysical (im)possibilities, as opposed to physical or logical ones.
Hi Andrew,
It is true that "the answer is trivial until an alternate possibility turns up in our observations." After all, that is why we call them "fundamental" physical constants. :-) But...
The problem with your whole approach here is that it begs the very question that's on the table. The only way to observe (or rule out) alternate possibilities is to start by acknowledging that they are precisely that--possibilities... and then, go looking for them. This isn't "running wild with speculation," it's doing physics. As Andrew2 pointed out, the whole point of science is to explain what we observe--not explain it away. "It is what it is because we observe what we observe" is not an explanation of anything.
Going back to my marriage analogy, Wonder Woman is not a valid comparison to Lisa or Kathy for one simple reason... She already has been ruled out. There's no question about the fact that she's a fictional cartoon character, and as such, not marriage material for your neighbor. On the other hand, according to your logic we have no choice but to assume that if we observe that he married Lisa, then she is literally the only woman on earth (or at least the only one he knows), and checking dating websites or his circle of friends and acquaintances for any other living female soul would be "running wild with speculation." That doesn't follow.
The same is true of fundamental physical constants. Not only is there no valid reason to assume fundamental physical constants can't have alternate values, there's considerable precedent for not doing so until it's been proven otherwise. Case in point, the cosmological constant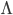 . The only reason Einstein even proposed it in the first place was that he didn't like the idea of an expanding universe and needed to postulate it to avoid one. When it was independently discovered that the universe actually is expanding, further observations placed its value at zero to within statistical significance and Einstein promptly referred to it as "the biggest blunder of my life." For the next few decades, every cosmology textbook in print treated it as such, and that was still the case when I was in graduate school. But cosmologists remained perplexed because... [wait for it]... there was no reason why it should just be what it is "because that's what we observe..."
. The only reason Einstein even proposed it in the first place was that he didn't like the idea of an expanding universe and needed to postulate it to avoid one. When it was independently discovered that the universe actually is expanding, further observations placed its value at zero to within statistical significance and Einstein promptly referred to it as "the biggest blunder of my life." For the next few decades, every cosmology textbook in print treated it as such, and that was still the case when I was in graduate school. But cosmologists remained perplexed because... [wait for it]... there was no reason why it should just be what it is "because that's what we observe..."
Or so we thought! Eventually, it was discovered that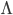 is, in fact, positive, and has the value I reported above. In 1997 the Nobel Prize was awarded for that discovery. Had physicists just assumed there was "no a priori reason to go and search for [other values] or even regard them as real possibilities" that discovery never would've been made.
is, in fact, positive, and has the value I reported above. In 1997 the Nobel Prize was awarded for that discovery. Had physicists just assumed there was "no a priori reason to go and search for [other values] or even regard them as real possibilities" that discovery never would've been made.
This "luxury" as you call it, is what makes science possible. If we made it a ground rule that "Observed = Necessarily Real" and "Unobserved = Necessarily Fiction," there would be no physics... and Aron wouldn't have a job! :-)
[BTW, the claim that Newtonian gravity and "Einstein's replacement" of it place no constraints on negative mass is incorrect. Newtonian gravity is a demonstrated low mass-energy limiting case of general relativity, and the equivalence principle renders negative mass impossible. If negative masses ever were observed, GR would be falsified and in need of being completely replaced.]
Best.
One minor correction to my last... It's negative rest mass of the sort that appears in Newtonian gravitation that's forbidden by GR. Negative energies are allowed.
Doesn’t GR allow imaginary rest mass, though (tachyons)? And yet we haven’t observed any.
The multiverse speculations are something new in the history of physics. Previously physicists searched for the constants and once the value was fixed by experiments, it was then fixed. Of course, the experiment could be refined and more precise values obtained. But they did not go on speculating the possible values the said constant would be taking in some unknown world.
What is more, they do not even speculate, properly speaking. They do not say that the electronic charge is 1.6e-19 coulomb in this universe, but 2.5e-19 in some other specified other universe. They just bandy about multiverses, and infinite possible values of constants etc. There is nothing specific. That's why I asked if any proposal for alternative self-consistent laws of physics exists.
Unfortunately I couldn't get back to this quickly so there's tuners coming at me from all directions. It’s like a tuner sandwich!
Andrew2,
I've not missed a point. Just like Scott's initial invalid analogy about marrying two observed possibilities, your analogy is also irrelevant here. It is perfectly reasonable to ask and explain why the sky is blue, because we observe lots of possibilities (not just blue) for our sky and others. This is the difference. THIS is the point. The possibilities are observed in those examples. When that's the case, it is perfectly reasonable to ask why one occurs. When it is not the case, we are still permitted to ask why, but the answer is trivial or useless until we observe more about the universe. This is not necessarily explaining it away permanently, but it is an acknowledgement that there is no fruitful justification in asking the question given our current knowledge. I think I see your point about logical vs physical possibilities, but I disagree that tuners are only supposing logical possibilities such as mathematical abstractions. We’re talking about physical constants here (nature), and as Scott said, there's no restrictions placed on constants by the laws, so by your definition, that illustrates he regards the possibilities as physical possibilities. Regardless, the problem is they have further assumed the physical possibilities were/are REAL to some extent. I'll elaborate as I respond to Scott.
Scott,
I'm happy to see we're on the same page about fundamental constants. Now let's explore everything you wrote after "but." :-)
You write that we must acknowledge possibilities before we may observe or rule them out. Then after acknowledgement, we may go and look for them. I agree this is how Physics is done, but that’s not something you or other tuners are doing. In fact, you’ve already assumed they really exist without “looking”, and have gone further to propose hypothetical explanations as to why we only observe one value. This is only speculation. Not Physics.
Your discussion of the cosmological constant further shows you are still conflating possibilities with what we can observe. You’re correct that Einstein proposed it without observation. That’s ok. That’s what we do sometimes. Then we go and try to observe what it is, and our best efforts at the time showed it to be zero. You are correct in this, but then you write,
“cosmologists remained perplexed because... [wait for it]... there was no reason why it should just be what it is ‘because that's what we observe...’”
And
“Had physicists just assumed there was ‘no a priori reason to go and search for [other values] or even regard them as real possibilities’ that discovery never would've been made.”
You’re absolutely wrong in your suggestions here. First, there is no evidence cosmologists remained perplexed that it should be zero, because as you can read in texts on cosmology or general relativity, everyone accepted a non-zero value (as Einstein eventually did) as an unnecessary assumption. Second, physicists then DID assume there was no a priori reason to search for other values. Until there was reason. Observed reason. The current value of the cosmological constant was not discovered because we thought it had to be another value. It was discovered because OTHER observations lead us to revise and refine our previous understanding and revisit the cosmological constant. This history can be found in any astronomy textbook. But regardless of this history, once again, our ignorance of the actual value does not mean that it actually was and could have been exactly zero. This is why the cosmological constant is actually not a case in point.
I’m sure we agree on how Science is done, but to clarify, I’m not suggesting unobserved = fiction. The best any scientist can say is unobserved = maybe fiction. Until we rule that out by observation, I’m sure you’d agree it’s a very prudent position to take. And note, I’m not even saying it can’t be ruled out. We just can’t seem to do it now. The problem with the tuning argument is it’s like saying unobserved = probably real. I’m not even saying that’s false, but you’d have to agree it takes a giant leap of faith to accept it and then go beyond to build upon that acceptance. This is what tuners do. I’m not saying it’s wrong, but it certainly isn’t fruitful. Case in point, your possible answers to questions involving the unwarranted acceptance of possibilities being probably real involve a currently unobservable god with unobservable divine action, or a currently unobservable multiverse with unobservable infinite possibilities. Neither of these are things we can scientifically build upon, and this makes sense because in the context of the tuning argument, they came from an acceptance that we cannot scientifically build upon at present. This is still my main point. Accepting unobservables as evidence supporting a premise in an argument makes the argument a poor one.
[BTW, the equivalence principle doesn’t necessarily render negative mass impossible. It’s simply a starting point in developing GR where we assume positive mass because that’s what we observe in nature. We may still determine solutions to the field equations that include negative mass. More fun speculation, but again, it’s just that … fun speculation. My favorite is the Alcubierre warp drive. Here’s another specifically singling out negative mass: https://arxiv.org/abs/1407.1457
Hello Andrew,
Forgive me for taking so long to respond to your last. Once again I've had a rather stressful week, but I'll spare you the gory details of that. :-)
We seem to be in a bit of a rut here. Interesting as this discussion has been, and with all due respect for the points on which we agree, the larger subject of fine-tuning in physics has been explained clearly enough, here and in other posts, and I see no point in continuing to belabor topics that have already been thoroughly dealt with. So let me just leave you with these final thoughts...
First... No, acknowledging possibilities is not the same thing as "[assuming] they really exist without 'looking'." I don't understand why we have to keep revisiting this... it's really not that difficult. The definitions of the words possible and actual are clear enough, and hardly synonymous with each other. There's no valid reason whatsoever to think it's impossible, even in principle, to go fishing without being convinced there are fish in the pond. I've fished all my life and I'm here to tell you, I've cast lures and flies into countless fishing holes believing it wasn't even likely there were fish in them, much less that said fish were "probably real." On many of those occasions, I was shocked by a hard strike and a landed fish... where I least expected one. Which is precisely why I continue to explore waters where fish are possible without being probable, much less a given. Physics is no different.
Perhaps it would be helpful to review how science actually works. As you rightly note, we do pretty much agree on its larger principles, but some crucial subtleties are being missed. As I've written elsewhere, science doesn’t deal in facts as most people understand that word. It deals with data. One begins with reproducible measurements of some observed phenomena, especially those that current theoretical frameworks cannot explain, like the values of some physical constants. One or more hypotheses are formed to account for them, and the most viable of these are developed into formal theories from which the outcomes of further, yet untested observations can be predicted. Perhaps some deeper theoretical framework and/or boundary constraints require these values... Perhaps they aren't really constant after all, but are varying at some very small rate we have yet to detect... Perhaps. Any of these may prove correct, or none of them. Either way, if we want to know, we put these theories to the test by looking for their predicted outcomes. Failure to observe them is known as a theory's null hypothesis and counts as evidence against it. And (this is important!)... our observations are as much a test of our null hypotheses as they are of our theories. Never, ever, under any circumstances whatsoever does any reputable physicist presume that unobserved = "probably real."
There's a term for "science" that admits theories or null hypotheses, but not both... it's called dogma.
Second... Regarding the cosmological constant, I'm not sure what "astronomy textbooks" you've been reading, but cosmologists are, and for many years have been, more than just "perplexed by its [near] zero value." The cosmological constant problem has been one of the biggest and most vexing issues in physics for decades. Not only is there reason to think it could have a non-zero value, quantum field theory, arguably the most successful theoretical framework in history, requires it to be astronomically larger than its observed value--a state of affairs that has been referred to as "the largest discrepancy between theory and experiment in all of science."
Nor did anyone just assume there was no a priori reason to search for "other values" and set that question aside until "other" observations led them to revise it. Why do think those "other" observations were being made in the first place...? The teams led by Riess and Perlmutter invested a great deal of time, effort, and expense to map global distributions of Type-1A supernovae. Was that because their wives were all out for bingo night at the Grange and there was nothing good on TV...? Those surveys were among numerous other efforts (e.g. - the COBE, WMAP, and Planck missions, the Sloan Digital Sky Survey, etc.) whose objective was to map and characterize the large-scale structure of the universe and its cosmological parameters. Over the years, studies like these produced increasingly refined measurements of such parameters, including the cosmological constant. The latter was known to be approximately zero, but only to within significant confidence intervals that allowed for the possibility of a small non-zero value. Increasingly broad and sophisticated efforts such as these relentlessly shrunk those confidence intervals, leaving less and less room for one to hide in... until it couldn't hide any longer. At no point in any of these studies did anyone presume that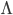 had to have a non-zero value. Indeed, the null hypothesis was the expected result, which is why the discovery was all the more shocking and Nobel-worthy when it was made.
had to have a non-zero value. Indeed, the null hypothesis was the expected result, which is why the discovery was all the more shocking and Nobel-worthy when it was made.
Finally... Regarding negative mass and the equivalence principle, I stand corrected. Although I can't help but notice that you referred to its possibility as the very sort of speculation that you claimed above is "not physics." Yet as your linked paper reveals, physicists do seem to think the question worth investigating.
Best.