There's a common notion floating around, due to Karl Popper, that scientific theories are characterized by the fact that they are falsifiable. The idea is that it is never possible to verify a scientific theory (i.e. the sun always comes up) because one day it might not happen. But it is possible that the sun might not come up some day, and then the theory is falsified. It must then be rejected, and replaced with something more complicated.
Now, let me confess right away that I have not gotten this idea by reading any of Popper's writings. It is an idea which has been popularized in the scientific community. You see, everyone knows what Popper said without having read any of it ourselves. It could be that if I actually read Popper's books, my idea of what he said would be falsified. So let me confine myself in this post to discussing Popperism as commonly understood.
If a theory is unfalsifiable (that is, if no experiment you could possibly perform would rule it out, then according to Popperism it is not a scientific theory. Among those who subscribe to Scientism, this is usually assumed to be A BAD THING™. (The way some people talk, if a theory is unfalsifiable, that means it is false!)
People often characterize bogus pseudoscientific ideas as unfalsifiable, because of the tendency of people who believe in them not to subject them to rigorous scrutiny. But this is clearly an oversimplification. True, there is such a thing as mystical Woo-Woo from which no definable predictions can be made, either because the ideas are not precise enough or because they don't relate to any actually observable phenomena. But many psuedoscientific ideas, such as homeopathy, reflexology, or astrology, can be tested experimentally, it's just that the people who believe in them don't like the results when people do!) I've heard people refer to Young Earth Creationism (YEC) as unfalsifiable. I think their reasoning must be the following:
1. YEC is unscientific and wrong.
2. I've been taught that when ideas are unscientific, the reason is because they are unfalsifiable.
3. Therefore, YEC is unfalsifiable.
In fact, though, the real problem with YEC is that it IS falsifiable, and in fact has been falsified many time over. If the universe were created about 6,000 years ago and we have to get all of the layers of fossils and rock from a single planet-wide Flood about 4,500 years ago, then there are a gazillion problems with observation. It contradicts the results of almost every branch of science which tells us anything about the past. (Adding bizarre extra ideas, like God created the earth with fossils in it in order to trick us into believing in evolution, may make YEC unfalsifiable, but it might be better to characterize this as pigheaded refusal to accept reasonable falsification.)
[Fun fact: if you interpret all of the genealogies in Genesis as being literal, with no gaps—which of course I don't—then it follows that when Abraham was born, all of his patrilineal ancestors were still alive, back to the tenth generation (Noah)! (This is using the Masoretic Hebrew text that omits Cainan, who is included in the Septuagint Genesis and Luke.)]
All right, digression over.
Clearly there is something right about the idea that theories ought to be falsifiable, yet not confirmable with certainty. Major scientific theories usually deal with generalities: they make predictions for a large (perhaps infinite) number of different situations. Normally, it is not possible to verify them in all respects, because even if it works well in many cases, it could always be an approximation to something else.
On the other hand, I think there are some scientific ideas which are verifiable but not falsifiable. Here's an example:
Ring Hypothesis: Somewhere in this universe or another, there exists a planet with a ring around it.
I submit to you that: 1) our observation of Saturn verifies the Ring Hypothesis, 2) when scientists verify a proposition by looking through a scientific instrument, that counts as Science, and 3) no possible observation could have falsified the Ring Hypothesis. (Even restricting to the Milky Way, eliminating planets with rings would be a tall order, impossible with current technology.) Therefore, there are scientific propositions which are verifiable but not falsifiable.
On the other hand, even if an experiment "falsifies" a theory, it could be that the experiment rather than the theory is wrong. As Einstein once said "Never accept an experiment until it is confirmed by theory". This witticism may seem to turn science on its head, but nevertheless it has a bit of truth to it. A while back, there was an experimental observation which seemed to suggest that neutrinos travel faster than light. Soon there were many papers on the arxiv trying to explain the anomaly. But it turned out, not surprisingly, that there was an error in the measuring devices. Usually, when a well-tested theory is in conflict with an experiment, and the anomaly has no particularly good theoretical explanation, it is the experiment which is wrong. Not always, but usually.
What this means is that we need a more flexible set of ideas in order to discuss falsification and verification. In particular, we ought to accept that falsification and verification can come in degrees—observations can make an idea more or less probable, without reducing the probability to exactly 0 or 1. The accumulation of enough experimental data against a theory should make you reject it, but it may be able to withstand one or two anomalous measurements.
The quick answer is that one ought to use Bayes' Theorem instead. This is a general rule for updating beliefs, taking into account both our prior expectations and observation. This goes not just for Science, but also for everything else. The only thing that makes Science special is that, due to a number of special circumstances, the process of testing through observation is particularly easy to do.
Even though falsification is not the best way to think about Science, it still works pretty well in many cases. In a later post, I hope to explain the connection between Bayes' Theorem and falsification. Usually we should expect good theories of the universe to be falsifiable, but in certain situations they don't have to be. Bayes' Theorem can be used to understand both the general rule, and why there are exceptions.
I think your views on Popper (that's *Sir* Karl Popper btw ;0p) are in broad alignment with the views of most current philosophers of science - that he gets something right when he talks about falsification as being central to science, but there's also something that's not quite right about it too. People generally agree that it's an improvement over the confirmation account of what makes science, um, science. But ultimately, as you point out, it falls victim to the same problems that confirmation faces...e.g., that there are cases where it's impossible to falsify a reasonable theory/hypothesis (*in practice* if not *in principle*), that you can always come up with post hoc explanations, that you can always question the reliability of the measuring equipment, and so on. Your take that confirmation and falsification come in degrees is quite aligned with Lakatos' insight: Scientific theories rest on a network of beliefs and assumptions, some of which are more core to the theory than others; such that, if there is an anomalous observation, the outermost, "auxiliary" assumptions are the first to go (e.g., the assumptions that the measuring devices are functioning properly, and other things of that nature). The auxiliary assumptions act as a protective belt surrounding the core assumptions (e.g., that energy is conserved, every action has an equal & opposite reaction, and things of that nature). These core assumptions only get challenged, shifted, and abandoned in very rare occasions, as Kuhn would say, at periods of scientific revolutions (Copernicus, Einstein, that kind of stuff). Ultimately, I like to think of falsifiability in terms of Kuhn's account - as one of the many aesthetics that factor into theory appraisal, but not always the most important one for any given scientist or any given theory appraisal (though sometimes very important). Speaking of which, I'm not ready to jump on the Bayesian bandwagon (Bayeswagon?) just yet. It strikes me as unfalsifiable! Not unlike the Drake equation, its virtue is that it's a useful tool for organizing thoughts and assumptions. You're going to have to convince me of anything further! ;0p
The whole notion of “falsifiability” is meaningless in mainstream physics.
The particle does not always travel through a single slit in a double slit experiment.
How do you falsify the above statement? You place detectors at the entrances, throughout or at the exits to the slits.
When you do this the particle is always detected entering, traveling through and exiting a single slit.
The notion the particle does not travel through a single slit is refuted by the evidence. It’s been falsified.
So, what does mainstream physics do? They ignore the physical evidence which refutes the notion the particle does not travel through a single slit and state that something else occurs when you don’t detect the particle.
What is that something else? Well, now mainstream physics can make up all sorts of stuff about a multiverse or many worlds or whatever nonsense it wants because you can’t falsify made up nonsense.
The notion the particle does not travel through a single slit is falsified by the physical evidence.
However, mainstream physics is so screwed up it can’t understand something as simple as the particle always being detected entering, traveling through and exiting a single slit in a double slit experiment is evidence the particle always travels through a single slit. It is the associated physical wave in the aether which passes through both.
Luke,
It's nice to know that some contemporary philsophers of science are saying some fairly sensible things. Thanks for the input. Even though I am an American and don't believe in such things, I apologize to SIR Popper for forgetting his title of nobility. I wish that I could call him SAINT Popper (Acts 26:29), a far better thing, but at least in his earthly life it appears from a cursury internet search that he did not know the Savior.
Kuhn (another great whom I haven't read, but expect to disagree with when I do) always seemed to me to be unnecessarily disrespectful to his elders when he appropriated Planck's dictum:
The idea you attribute to Kuhn about theories being protected by auxilliary assumptions which (at first) we are more willing to discard seems entirely sensible. However, I note that we didn't actually need to change any of our ideas about how equipment works in general to save ourselves from faster than light neutrinos. We only needed to change our view that the equipment in the OPERA experiment was properly calibrated. (Indeed, now that it is fixed and is giving sensible results, presumably we all go back to believing that it is probably properly calibrated.)
I also want to observe that this is not quite the same thing I was saying when I said falsification and verification come in degrees. I was talking about my Bayesian degree of confidence in a particular proposition/i>. But of course, in general there are multiple propositions running around, and when we update our credences according to Bayes' Law, this will generally require us to start by doubting the principles which seemed least certain to us.
Regarding your doubts of Bayesian epistemology: I don't think that it has to be falsifiable. Bayesianism purports to say how an idealized rational agent should adjust their beliefs based on evidence. In principle, the way you would support this is by thinking about lots of different possible situations (real or counterfactual) and ask whether it gives a sensible prescription in all of these situations. Then you compare to other epsitemologies and see which is better. Since the situations don't have to be actual, I think this is in principle a purely a priori inquiry. I think that means it doesn't have to be falsifiable, any more than 2+2=4 is falsifiable. But I also think it works great when applied in practice (just like arithmetic is a highly practical art).
Anyway, there are various Dutch book arguments which say that if you have to accept or decline bets on various propositions at various odds, and if we define your probability credences based on which bets you take, then EITHER your credences can be represented as following Bayesian rules, OR you might accept a set of bets which is guarenteed to lose you money. To me this is as close to a "proof" as one is likely to get in philosophy.
Welcome to my blog, mpc755.
The interpretation of quantum mechanics is a notoriously tricky subject. There are a number of different interpretations. People who hold different interpretations all agree on how to calculate probabilities in real experimental setups. Hence there is no experimental way to distinguish between them. Instead, we have to use some combination of logical consistency and theoretical elegance to determine which is the best. Really, it's a question in metaphysics, not physics.
All metaphysical theories involve postulating some sort of additional stucture, not directly observed, in order to make better sense of what we do see. Your Bohm-like "physical wave in the aether" is just as much an example of this as Copenhagen or the Many Worlds Interpretation. There's nothing wrong with this in principle, the question is just which type of postulates seem most reasonable. (Personally I think that MWI is logically inconsistent in its treatment of probability theory, but obviously other people disagree.)
However, the rules for calculating probabilities for different events happening are plenty falsifiable. You just do an experiment and see if the frequencies of outcomes agree with the predicted probabilities, within the relevant error bars. If you can agree with the rules for doing this, then we mainstream physics will be happy to have you.
Anyway, it seems rather cynical for you to condemn my entire profession based on this one issue, which even mainstram physicists would agree is controversial. Just because pop-science books and intro-level courses use certain heuristic concepts to try to explain QM to people, doesn't necessarily mean that they are Articles of Faith which you have to accept to be a physicist.
I don't know enough about your "physical aether waves" interpretation to say whether it agrees with experiment, but if it does, great! We can add it to the long list of alternative interpretations of QM people have come up with. On the other hand, if it doesn't agree with experiment, or if we can't understand what it is saying, then there might be a problem.
The main issue with postulating a "physical wave in the aether" to guide the particles, comes in situations where there are 2 or more particles running around. In situations like that, the guide "wave" needs to be a function, not living in the three space coordinates, but rather in the space of all possible configurations of the particles. But once you say that, it is obviously no longer a conventional wave of a usual sort. It's a really weird and counterintuitive type of wave. But if you're comfortable with that metaphysics, great! All of the choices on the table involve assuming something really bizarre is going on.
Aron, would you like to be more specific about the inconsistency you find in MWI's treatment of probability theory?
g,
At some point, I should devote a blog post to this subject. But before that, I'll need to explain QM some. So as not to drive you mad with curiosity before then, here's a very brief explanation:
If all branches of the wavefunction truly exist as separate "worlds", that seems to me logically equivalent to saying that everything that can happen, happens with probability one. But that's in flat contradiction with the Born rule, which says that some events have a greater probability of occuring than others. I don't even know what it would mean to say that all physical possibilities exist, but that some of them exist more than others. Existence is not something that comes in quantitative degrees!
OK, thanks.
I don't see that there's a contradiction here. MWI says (kinda) that everything happens-somewhere-in-the-multiverse with probability 1, but it doesn't say that everything happens-on-this-particular-occasion with probability 1, and it's the latter that would contradict the Born rule (or everyday probability theory). (Compare a very-large-universe theory that has a universe large enough and random enough that there are almost certainly vast numbers of "versions" of us (with our present surroundings and history) in it. Maybe even an infinite universe, with infinitely many copies of us. Then, e.g., when you roll a die, "with probability 1" there's some version of you somewhere that rolls a 6. But there's no contradiction between that and the fact that (with the usual idealizing assumptions) the probability that you roll a 6 on this occasion is 1/6 rather than 1.)
I agree there's something of a puzzle about how wavefunction amplitudes produce probabilities. But one can make an argument along the following lines (there's a famous paper by Wallace that goes into more detail, though his language is a bit different from mine; I think it's expanding on some ideas of Deutsch, and from what he says about Deutsch it seems possible that Deutsch's approach is more like mine below).
Assume (this, if anywhere, is where something gets smuggled in) that sufficiently small wavefunction changes (measured in the "obvious" norm) correspond to small changes in probabilities in some sense, and in particular that if you decompose the wavefunction into orthogonal bits one of which has a tiny norm then the probability associated with the latter is very small. (That's shorthand for a statement about limits.) Then I'm pretty sure you can show that histories in which frequencies diverge badly from the ones you get from the Born rule have very small measure and hence (in the limit) tiny probability. In other words, if you're willing to assume that tiny measure => tiny probability, then that suffices to show that "the Born rule almost always holds approximately in the long run".
Wallace's paper takes a slightly different approach, making not a substantive assumption about probabilities (infinitesimal measure => infinitesimal probability) but a normative assumption about preferences (agents' preferences should be continuous functions of the wavefunction), and deducing (with a bunch of other very reasonable axioms) that rational agents should act as if they predict outcomes in accordance with the Born rule.
(I should maybe stress a bit more that "tiny measure => tiny probability" is a consequence of "probability is a continuous function of the wavefunction", which may be a more plausible axiom. I should also add that I am not a quantum physicist, or any other sort of physicist, and any amount of what I've written may be wrong, though I'm pretty sure the basic ideas are OK.)
g,
I'm familar with attempts to smuggle in the Born rule, and they seem rather unconvincing to me. The elegance of MWI is popularly supposed to be that all need is the wavefunction---no need for any additional rules like collapse. But in fact, as you point out, you do need some auxilliary assumptions, in all the rules that you point out. And in particular, the assumption that "sufficient tiny norm events never happen" seems rather contrary to the premise that "all possible events happen".
It seems to me, that once you've specified everything that IS (and saying either 1) "every possibile outcome happens" or 2) the wavefunction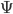
is all that exists seem to me to be such specifications), there is no more room for additional arbitrary assumptions. You've already said everything there is to be said about the universe. That would make MWI incoherent.
Actually, about such situations I would be inclined, hesitantly, to say that it is also meaningless what you roll (and therefore that we know we don't live in such a universe). When you roll a die, there are infinitely many versions of you which get a 6, and infinitely many versions where the die explodes and you die, and infinitely many versions of you where green monkeys pop out and start torturing you to death. They are all equally "real", and they occur the same cardinality number of times. Unless you're the sort of person who thinks you die if you enter a star trek teleporter, I think the only correct thing to say is that you would have ALL of these experiences.
Anyway, the question of how to do probability theory in such "mutiverse" type settings is highly controversial, and I'm not aware of any satisfactory general prescription which doesn't lead to horrible paradoxes in certain cases. But, provisionally, because it seems to me the least absurd, I incline to the view that by far the best way to explain the (seeming fact that) some things happen but not others, is that (in reality) some things happen but not others. This requires that the universe not be too large and uniform.
(I know that this is all rather off topic, and you've said you're going to be posting on this issue in the future -- so unless you specifically request otherwise this will be the last I have to say on the matter in this discussion.)
I really don't see how the word "smuggle" is a reasonable description of what I described. We have the wavefunction. We have an obvious metric on the space of possible wavefunctions. I remark that the axiom "probabilities are a continuous function of Psi" is enough to get you (close enough for practical purposes to) the Born rule. Where's the smuggling?
But I never suggested making the assumption that sufficiently-tiny-norm events never happen. I suggested making an assumption that implies that as norm -> 0, the probability of the event happening (on any particular occasion) also -> 0. That's an entirely different matter.
It seems to me that you should have, at least, a niggling feeling in the back of your mind that you're deriving too strong a conclusion from too little information, when you say "therefore we know we don't live in such a universe".
I suggest the following thought experiment. Consider a one-parameter family of universes, all very much like this one (and, in particular, all having us in them) but with parameterized size. Once the size gets large enough, there are almost certainly "copies" of us with indistinguishable life histories such that (e.g.) any given die roll comes out each possible way; and apparently you know on (for want of a better term) metaphysical grounds that that's absurd and meaningless and "therefore we know we don't live in such a universe". For smaller sizes, this doesn't happen and (so far as I know) you're happy regarding us as living in such a universe. So what does the transition from possible to impossible look like? Is a world where there is, let's say, a 10% chance that there's just one other indistinguishable copy of you "meaningless" and impossible? One where there's a 0.01% chance? 10^-100? Even in our world, and even assuming it isn't terribly large (for all we know, last I heard, it might well be), the probability isn't zero. Should we be saying that Pr(roll a 1) = ... = Pr(roll a 6) = something just a little bigger than 1/6?
It seems to me that that whole line of thinking must be wrong. The probability that you roll a 6 isn't made any larger by the possibility that a copy of you somewhere else might be rolling a 6. Your probabilities have to add up to 1, not to 1 + a fudge factor accounting somehow for the possibility that there are other versions of you elsewhere.
And it also seems to me that if all these finite-but-ever-larger universes are OK and give us the same probabilities (as they must) then their infinite limit is also OK and gives us the same probabilities; and that cardinality is a mere red herring. I should in fairness add that although I think I've just given a reason to think it's a red herring, that isn't "my" reason -- it simply seems obvious to me from the outset that "they all have equal cardinality" is no more reason to assign equal probabilities than e.g. the fact that (assuming a traditional continuously-divisible spacetime) the states-of-the-world in which a die comes up 1 and comes up not-1 "have equal cardinality" is reason to assign equal probabilities to those.
A quick note about Noah and Abraham - I don't see why you think this is a far-fetched idea. It actually seems to be implied by the text itself. What did Jacob say to Pharaoh in Genesis 47:9? "The years of my pilgrimage are a hundred and thirty. My years have been few and difficult, and they do not equal the years of the pilgrimage of my fathers".
He lived to be 130 years old, but his years were *few* and *shorter* than that of his ancestors. By all accounts, even incidental ones like this, human longevity shortened dramatically in those years. In addition, if you have a group of people who are living that much longer than their offspring, you can see where the Greek and Roman heroic stories come from. You have a group of people who really do seem to be immune from death giving birth to children who are mortal. Eventually they did die, but this must have been how it seemed to those living at the time.
Welcome to my blog, Jonathan. It is of course true that Genesis seems to portray prehistoric human beings as living longer than other humans. There are also other ancient texts which describe mythologically long lifespans (e.g. Sumerian kings reigning 72,000 years, which seems excessive even by the standards of Genesis).
However, archaeological evidence shows that prehistoric people (at least those whose remains we can examine) did not live longer than modern day humans; in fact their life expectancy, and the age of the oldest people, are noticably lower. Thus, in general, they did not live longer than us. Which should not be surprising given the much worse medical technology of that time.
If long life were only achieved by a tiny fraction of the population, then of course we would not necessarily know it from archaeology. One could imagine that God supernaturally extended the ages of certain people (given the basic facts of human biology as we know it now, I think this would require a miracle), but we would not be able to scientifically test this unless those people were a part of our sample. This seems especially likely in the case of Abraham, where the whole point of the story is that he and Sarah were much to old to have a child, his body being "dead" as Paul says---and that he had faith anyway that God would do the impossible.
But long lifespans are hardly the worst conflict between modern Science and a literal interpretation of Genesis. The fact is, that any Christian who accepts the modern scientific consensus must interpret the early chapters of Genesis nonliterally. Leaving aside the age of the earth and human evolution, the geological evidence simply cannot be squared with a universal Flood. Thus, at least the extreme old ages of the antediluvian patriarchs are squarely inside a portion of the text which we know for other reasons to be mythological (although nonetheless divinely inspired by God, and revealing deep truths in a symbolic way). The symbolic nature of these ages seems reinforced by the fact that some of them seem to have numerological singificance (most strikingly Enoch (365) and Lamech (777)), and that they keep coming tantalyzingly close to 1,000 without ever reaching it, suggesting the inadequacy of even the longest lifespan for attaining complete fulfillment. This lesson from Genesis will be of even greater practical significance if future medical technology allows us to extend the maximum lifespan beyond 120 years.
You classified Homeopathy as unscientific 'idea', LOL??!
Instead of embarrassing yourself further, please EDUCATE yourself before stating another UNscientific opinion about the healing power of homeopathy!
http://dialecticalhomeopathy.com/
http://hpathy.com/clinical-cases/
http://www.homeohome.com/about-swasthya-clinic/cured-cases.html
http://www.modernhomoeopathy.com/cases.htm
http://www.homeopathy.ca/courses_det04-review.shtml
... and many, many more...
[Can't help but notice that these links consist primarily of individual case studies, and that while some of them are dramatic, none of them involve double blind tests, which totally ought to be possible if homoeopathy isn't just the placebo effect.---AW]
I personally have only used Homeopathics on my family (ear infections, croup, flu, colds, warts and other lovely childhood things) They have always worked which is why I continue to first seek out a treatment using homeopathics. If at any point a cure is not found I'd seek the help of medication BUT 8 years and 3 kids later no antibiotics, fever reducers, steroids etc. have been needed. (Not to say that will alway be the case!)
I am continually told by 2 friends who are nurses that homeopathics are bunk. (while their kids tend to have longer fights against illnesses than mine) But I ask them, "why should I change what is working?" I might not understand the science behind it (I have read Margeri Blackie ' s The Patient, Not The Cure... that's all the studying I've done on this topic) but my "mom commonsense", based on the evidence in my life and the lives of my family, is that homeopathics work.
I'm cool with someone saying homeopathics are "non- scientific" because I know they can't be tested like medication. But being "non-scientific" doesn't mean they don't work or have a place in the area of healing/wellness.
Sarah,
How do you know the improvements weren't just due to the placebo effect? And if they work, why would it be impossible to test them?
Can a placebo effect be 99% affective for 5 different people on multiple illnesses?
Honestly Aron... I taught kindergarten and now stay at home with my 8, 5 and 2 year old. I consider myself to possess intelligence BUT I lack education (in many areas ;-) this is one reason I read your blog) I don't know much besides what the definition is of the placebo effect.
In the area of Homeopathics I use common sense... it had worked for ALL of us in different areas (like I listed before) So when my friends who are in the medical field tell me I should stop doing what has worked and start doing what they do which doesn't work as quickly or effectively (in a few cases) I find their unwillingness to even try homeopathics for themselves to be a bit silly.
But to them I'm just a teacher who knows nothing in the area of medicine so why listen to me ;-) My kids are very healthy kids so for that I'm grateful!
As for testing homeopathics, I was privy to a debate between a medical and naturopathy doctor. Sorry it's been well over a year. What I understood was that one of the objections by the medical doctor was that homeopathics can not be tested like medication. That the claim of "like curing like" by the use if a substance's energy can't be tested using the scientific method.
If this is true or not, I have no idea. I took the doctors words in good faith since I am not educated in the areas science and medicine.
Again, they work for us (or at least we think they work for us ;-) ) and we don't have to mess with the lovely side-effects of some medication (constipation and drowsiness in a child are super fun and every mothers dream ;-) )
Good point with the Ring hypothesis. However, in this form it's falsifiable, because in principle it's possible to check all the planets (you only need logical possibility, not the empirical one). But it can be changed to "There exists a possibly non-observable planet with a ring around it", and now it's as unfalsifiable as can be ;)
Welcome Ciach,
I don't see why you say falsifiability only requires "logical possibility" to falsify the theory. Who says that?
I'm pretty sure that when people talk about falsifiability, they mean that it's actually feasible for some future experiment to falsify the theory. Not that some logically-possible (but actually physically-impossible) measurement would allow you to do so!
Practically speaking, it's impossible to check all the planets in the observable universe. And checking outside the observable universe is probably physically impossible due to the absence of FTL travel. Let alone checking to see whether there are any other universes besides this one.
"People often characterize bogus pseudoscientific ideas as unfalsifiable"
Astrology I regard as pseudoscience not because it is unfalsifiable but its computational procedure does not fit the scientific procedure.
A scientific computation takes many inputs but the outputs are fewer. Thus, the information content of the output does not exceed the information content of the inputs.
In astrology, they ask you for 1-2 inputs but these inputs are able to produce indefinitely many outputs.
There is a generation of information, not possible from any computational procedure.
Macotul,
NO! That is very close to the direct opposite of the truth. There are lots of scientific theories that take a small number of inputs, turn a mathematical crank and calculate a large number of outputs. For example, Quantum Electrodynamics (QED) requires only a single real number as input (the fine-structure constant) and outputs an enormous amount of information (many, many numbers to many degrees of accuracy) about how electrons and photons scatter.
It is much closer to being true that a theory is worthless if the information in the inputs exceeds the information in the outputs. Because in that case, there is a high probability that the theory makes correct predictions only because you tuned the inputs until you got the right outputs, and not because of actually correctly describing the physics.
So trying to get a large number of outputs from just a few inputs is what all good scientific theories do!
The reason astrology is nevertheless bad, is because their outputs don't take the form of verifiable experimental results. They take the form of vague descriptions of you personality and life outcomes, which people accept as accurate due to the Barnum effect. (And when people do proper controlled scientific experiments, they almost always get null results.)
Also bad is the complete absence of any plausible scientific mechanism whereby the position of the planets could affect human behaviors in the desired way. This makes it very unlikely a priori. (Although if the experiments showed strong enough results, we would have to accept it anyway and cope with the consequences---that's how science works!)
When people ask me for my birthday for astrological purposes, I tell them that if astrology really worked, they ought to be able to tell me my birthday!
"When people ask me for my birthday for astrological purposes, I tell them that if astrology really worked, they ought to be able to tell me my birthday!"
Aron, this statement is priceless! Definitely one that's going in my repository of pithy quips! :D
Aron,
"Quantum Electrodynamics (QED) requires only a single real number as input (the fine-structure constant)"
So, even the electron and proton masses are not required?
Or the values of electron charge, Planck's constant and the speed of light separately?
I know extremely little of QED but I thought that the expansion of various cross-sections, for instance, in QED was made in the powers of the fine-structure constant. But that QED requires no other physical input --this view is novel to me.
"The reason astrology is nevertheless bad, is because their outputs don't take the form of verifiable experimental results"
On the contrary, the astrologers are forever making falsifiable predictions. They are continually falsified. But due to some strange irrationality in the people, they still attract customers.
"They take the form of vague descriptions of you personality and life outcomes"
You have perhaps acquainted only with very debased astrologers. Traditionally, the astrologers did their computations and still do, in India for instance. That they ask for your birthday MEANS that they do some kind of computation. It is missing the point that they do not KNOW your birthday. They do not claim to be prophets but calculators.
Aron,
Surely, to predict an experimental result, many quantities need to be known, apart from the cross-section.
The geometrical information, the various areas, lengths, not to mention the time duration.
All these would be required if one aims to predict--how many scintillations there are going to be at a particular spot in a screen placed so and so distance away from such and such target, with the projectiles coming to this velocity.
Mactoul,
With respect to QED:
1) I was only counting dimensionless constants (those without units) because the numerical value of the dimensionful ones like the speed of light, Planck's constant, and so on depend on your choice of units, and you can select your units to make them equal to 1. See here for an explanation.
2) I was also thinking about the dynamics of electrons and photons only. If you include protons as well, then you would need to know the dimensionless ratio between their masses. And if you include more kinds of particles there will be a few more numbers. The point remains that you can predict a lot of numbers (the results of an arbitrarily large number of possible experiments) from just a handful of numbers.
3) I am also not counting initial conditions for a given experiment as input numbers, because those can (in an ideal experiment) be determined by the experimenter. You can think of the theory as making a large number of "if you do this... then this will happen (with this probability)" statements, and the point is that an infinite number of these can be predicted using a finite number of constants.
4) But even if we count the initial conditions of an experiment as inputs as well, there is no reason why one could not successfully predict more numbers then there are inputs. Good scientific models are predictive!
With respect to astrology, I agree that in principle it is falsifiable with rigorous enough tests, but most astrologers try to keep their predictions vague enough that people won't feel like it was falsified, but will instead grab onto potential confirmations.
Consider one of your non-debased traditional astrologers. Suppose that he asks for my birthday so he can calculate my fortune. Well, in principle he should be able to deduce my birthday by doing the calculation 365 times (once for each possible birthday) and then letting me know which birthday matches the events in my life that have already happened. (Such a test would of course require letting the astrologer know whatever non-birthday information about my life they thought they could predict.)
Pop American astrology predicts personality from month of birth, so if that worked they should be able to deduce my month from my personality, if they know me well enough. I am aware of the fact that traditional astroological methods are a lot more complicated than this and depend on the positions of planets as well as the sun.
Incidentally, because of the procession of the Earth's axis, these pop American horoscopes are all off by one month now anyway! Strange how few astrologers seem to have noticed...
"Somewhere in this universe or another, there exists a planet with a ring around it."
If you had read you Popper you would know that "strictly existential statements are not falsifiable. We cannot search the whole world in order to establish that something does not exist, has never existed, and will never exist. It is for precisely the same reason that strictly universal statements are not verifiable. Again, we cannot search the whole world in order to make sure that nothing exists which the law forbids" (Popper, 1959[2002]:40).
Aron.
On the lapsed question of whether a scientific calculation requires more inputs than outputs, you wrote
"Good scientific models are predictive!"
Yes, they are predictive but only because good theories have a formal procedure to calculate. Having a formal procedure requires certain inputs. Now, to me it is not at all obvious why a good (or any valid) procedure should be able to output indefinite number of outputs from a constant number of inputs.
Pls note that as I made the point on 17th April, prediction means prediction about an experiment and not just a theoretical calculation. Hence I do not accept your characterization
"You can think of the theory as making a large number of "if you do this... then this will happen (with this probability)" statements, and the point is that an infinite number of these can be predicted using a finite number of constants. "
This is so since we are comparing with astrology and the astrologers do make predictions about particulars. A particular individual and a particular time. So, physics also needs to do the same.
If one makes this comparison, one finds that physics requires indefinite numbers of inputs to output indefinite number of outputs. Unlike astrology.
Janvier,
Thanks for providing the quote. I did a websearch for the chapter in which Popper says that, and he goes on to say that: "on the basis of the criterion of demarcation I have adopted I shall therefore have to treat strictly existential statements as non-empirical or `metaphysical'." (And therefore, it appears, unscientific.)
That sounds like an incredibly bizarre definition of these words.
Mactoul,
You are completely unteachable! I gave a specific example from science of a model (QED) which makes an indefinitely large number of predictions from a small number of parameters. (Whether it is one or a few, does not matter for the point I am making.)
Needless to say, QED is not a mere mathematical calculational device that has nothing to do with observation; rather it is used all the time by scientists to predict the results of actual experiments!
Although you admit you know "extremely little of QED" yourself, you also seem to be unwilling to believe my word as a physicist about properties of this theory, and instead set about to dogmatically correct me about it. You are free to disagree with me about matters of philsophical interpretation, but you should at least give me credit for knowing some elementary facts about my own field of expertise.
What benefit do you gain from these discussions, if you are unwilling to ever admit that you might be wrong?
By the way, the statement "All elephants are more than 10 feet away from me" is formally universal yet verifiable, while the statement "There exists cash that is in my wallet" is formally existential yet falsifiable. Neither of these statements require an unlimited search.
Aron,
I regret sounding somewhat brash. ?My apologies.
I totally accept your authority on QED. My comments do not dispute your points 1 and 2--that is QED and relate to points 3 (which is rather subjective) and 4 (for which you provide no reason).
In any case, this is a very minor thing.It is just an idea I had about demarcating science from pseudoscience by considering alleged computational procedures of the pseudosciences. The idea is probably wrong.
Aron,
Your point 4.
"Good scientific models are predictive!"
Prediction means prediction in time. At time t_1 one predicts situation for time t_2.
Does it has a bearing on relative number of inputs and outputs? To seems it seems that even if one requires 10x quantities at t_1 to predict 1 quantity at t_2, it is still a prediction.
Mactoul,
Thanks for your apology, and sorry if I lost my temper too quickly. It is possible that some of the difference between us is just a difference of terminology. What I am talking about is the number of parameters that appear in a theoretical model (not experimentally controlled or observed numbers) and comparing that to the number of predicted numbers (including conditional observations given certain inputs as predictions.)
In general, if you have a theory with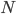
different parameters, for algebraic reasons you need to observe 
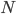different experimental parameters just to fix the value of these parameters themselves. Thus, you usually need at least 
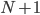different measurements to meaningfully test the theory itself. (This is just a rule of thumb, since there may be situations in which one of the parameters is irrelevant for the experiment and can be ignored entirely, or cases where certain outcomes can't be obtained from any value of the parameters due to nonlinearities, e.g. if 
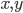are real-valued parameters and our theory says that 
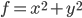, then a single measurement that 
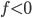will falsify the theory.)
Aron,
Hopefully, you would reconsider the idea that we can separate out some pseudosciences by pointing out how their (alleged) computational procedure differs from the procedure employed in physics.
Classically, a system of N particles is fully described by 6N independent numbers--3N position coordinates and 3N momenta at time T0.
This predicts at time T1, precisely 6N independent numbers-3N position coordinates and 3N momenta. So, there is a conservation of information. If we were to include chaos effects, there is actually a loss of information.
But, in astrological computations, there is no such loss or even conservation. Given a few numerical inputs, potentially all the information about future can be calculated.
I think you are confused a scientific hypothesis and an observable scientific fact.
To test the validity as a scientific hypothesis of a statement I present my trusty unicorn:
Hypothesis "Somewhere in this universe or another, there exists a unicorn".
That is as clear as an untestable and non-scientific hypothesis goes.
If I show you a unicorn in my garage, then it becomes a scientific fact. But the statement is no longer considered a hypothesis at this point.
To push the absurdity further, let's use the god hypothesis: "somewhere in this universe or another, there's god". Now that is clearly a non-scientific hypothesis. But suppose god appears, and let you measure him, and through that experiment prove that himself is indeed god. Now the hypothesis is no longer a hypothesis: it becomes an experimentally confirmed fact.
The problem with unfalsifiable hypothesis is that there's no objective way, other than dumb luck, for the scientific method to look for an answer whether the hypothesis is confirmed or rejected. Because there's nothing to look for, it is considered unscientific.
Yes, a falsifying experiment can be wrong. But the idea is that the experiment can be refined further if we work hard enough, and a bad experiment can be proven to be a bad experiment by someone else. Although it might be long and hard, it is possible to obtain an answer. That's the key difference.