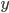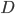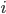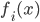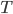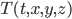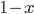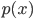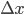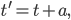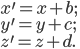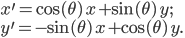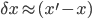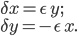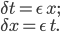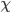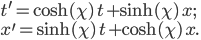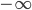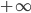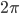Recently I ran across a pretty good explanation of the Higgs mechanism (hat tip Siris) by a certain Rob Knopp, which I thought I'd link to because of its connection with my previous post on fields. When I first looked at his blog, it seemed like maybe I'd found a kindred spirit: someone who blogs on science while identifying as Christian. Unfortunately, it turns out he actually denies almost all traditional Christian beliefs. On this blog, religion won't mean something watered down until it makes few if any factual claims. Instead I adhere to the red-hot supernaturalist "original brand" of Christianity that includes real miracles, a divine Incarnation, Atonement, inspired Scripture (including the Old Testament), the Second Coming, etc. Just in case you were wondering.
However, what really stood out to me from the last link was this throwaway line about medieval culture:
[Jesus] lived an errant life, eschewing the temporal power that monarchs would later claim was justified by the "divine right of kings," even eschewing extreme temporal influence. He preached the opposite of a lot of medieval social philosophy: the poor are not lesser humans and thus worthy of their lot, but if anything exalted. (Blessed are the poor, and all of that.)
Assuming that this was meant as a criticism of Medieval Europe (and not, say, the caste system of Medieval India), this is almost as far off base as if he said that Medievals had landed on the Moon. The Medievals did not believe that the poor are "lesser humans and thus worthy of their lot". It would be much more accurate to say that they believed that the poor were superior humans and that poverty is, not indeed strictly necessary for salvation, but highly desirable for anyone wanting to live more spiritually. Which explains all those people who swore vows of poverty in order to live in monasteries. It's almost as though they were familiar with the teachings of Jesus on the subject of poverty!
It's true that Medieval Europeans believed that the rule of earthly Kings was ordained by God. But the claim that so-and-so was the rightful King of England originally had nothing whatsoever to do with spiritual superiority, any more than your claim to own your car, or the President's claim to be legitimately elected, implies any notion of being spiritually superior to other people. Medieval Christians (like Ancient and Modern Christians) believed that God has ordained the existence of human governments to enforce justice, and that therefore (barring exceptional circumstances) it is our duty to obey whatever government one happens to live under. There was indeed a much more extreme theory of the "divine right of kings" that basically said that the monarch could not be resisted under any circumstances whatsoever. However, this theory was popular, not in Medieval times, but rather the Early Modern era (roughly the 16th-18th centuries).
As St. Chesterton pointed out, people are happy to accuse almost anything that seems old and bad as "Medieval" without checking to see what Medieval people actually thought and did. In reality, prior to the Renaissance, the Medievals:
- invented Academia as we know it, and founded the first Universities,
- strongly believed that one could discover the nature of the Universe using logical reasoning based on appropriate authorities,
- held in high regard ancient pagan learning and culture,
- like all educated people after Aristotle, knew the Earth is spherical and that the universe is huge compared to the Earth,
- prohibited military attacks on civilians, and tried to restrict war to certain days,
- ended nearly all chattel slavery in Europe (but see below),
- developed the notion that government must respect certain human rights (in feudalism, serfs were tied to the land but had customary rights which the lord was required to respect),
- officially taught that witchcraft was impossible, and that the popular belief in witches was a superstition to be discouraged.
Yes, you heard that right. They didn't burn witches. They did burn heretics, but those were real whereas witches were a figment of the peasants' imagination. Witch trials didn't become popular until the supposedly more enlightened Renaissance and Early Modern Era (mainly 1484-1750). Even then they didn't burn witches, they hung them. (What about all that stuff about dumping the witch in water to see if she floats? You know, either she floats and is convicted, or she drowns and is posthumously acquitted. Of course, no one would actually be so stupid as to devise a trial system that kills the innocent on purpose. In reality, the witch-hunters would pull those who sank out of the water before they drowned.)
The early Medievals did occasionally use trial by ordeal, when the evidence of guilt was doubtful—for other crimes than witchcraft, which they didn't believe in, remember! However, the trials actually appear to have been rigged to produce acquittals. In any case, these mostly ended soon after 1215 when the Church refused to allow priests to cooperate. In England this method was replaced with trial by jury.
The Modern Period also brought the racist version of the slave-trade into the world. Unfortunately, because of failure to turn the other cheek when pagans or Muslims would capture Christians as slaves, some slavery of non-Christians was permitted. Unfortunately, this meant that slave-traders were in existence when the New World was opened up...
The idea that the Medieval scholars believed the earth was flat is a lie invented in the 19th century by rationalists eager to find a historical precedent useful for mocking creationists, as documented by the historian St. Jeffrey Burton Russell here and here (I haven't read his book but I've seen him talk). For more information about the actual Medieval worldview, you can't do better than reading St. Lewis' wonderful book The Discarded Image. I should have put a gazillion more links in this post, but you all know how to use Wikipedia.
The idea of inevitable moral progress with time is much easier to believe if you only have a superficial notion of history. I do think that we've made important progress in justice over the past 2 or 3 centuries, but notice that a lot of these involve undoing the moral mistakes of the Early Modern era. Like all eras, the Medievals had many moral blind spots. But then again, so do we.