I've been SUPER busy this month what with:
i) faculty job interviews at a couple places,
ii) a bad cold, thankfully now over,
iii) a minicourse I'm currently teaching at the University of Maryland.
In the absence of a more substantive post, you can console yourself by pondering the following snapshot of my whiteboard.
Note: the cartoon has nothing to do with the equation above (or the sentence partially displayed below). But feel free to try to figure out what the equation means, if you can!

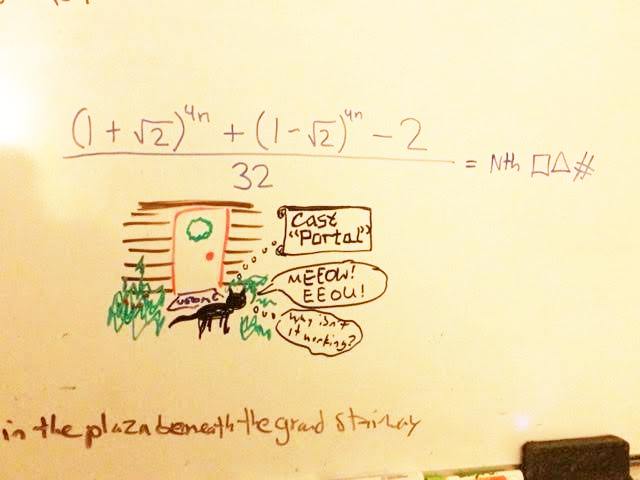
The equation is always equaled to the variable which has been inputted. Now what that means with respects to physics... no clue lol.
Aron,
We rapidly reach extremely large numbers for relatively small values of n. For example, for n=0, f(0)=0, f(5) = 1,413,721, and f(10) = 63,955,431,761,795. Obviously you are NOT testing mathematics or physics; however, the property of the function are rather interesting: Its hugely exponential behaviour, the fact that zero is the “vertex”, and the symmetry about it, are all clues to the metaphysics of “undivided looking”.
So here’s my metaphysical take:
Exponential behaviou = God’s omnipotence
Zero origin = Everything in life originates from God
Symmetry = Life is full of geometrical symmetry: the body, the heavens, etc. God is the ultimate Geometer.
Thanks.
So... any good news about the job offers? :D
I kinda figured from the hefty hint on the RHS that the equation was just a formula for the nth square triangular number - the first 10 or so values for n that I subbed in seemed to corroborate this. I'm having a harder time proving it though...
In the numerator, the term (1-2^0.5) = -0.4142++++, which means (1-2^0.5)^4n quickly goes to zero as n get larger and larger. So f(n) is approximately ((1+2^0.5)^4n -2)/32.
The error of approximation in percent is 0.09 for f(1) and almost 0,0 for n>1.
So the nth square triangular number (the clue) is almost exactly ((1+2^0.5)^4n -2)/32.
Andrew2,
Yes, it is a formula for the nth square triangular number. I figured it out myself, although it is by no means original.
To begin to see why it is true, note that a square number is of the form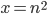 while a tringular number is of the form
while a tringular number is of the form 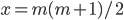 .
.  and
and 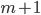 are coprime, therefore their prime factorizations have nothing in common. Hence, in order for
are coprime, therefore their prime factorizations have nothing in common. Hence, in order for 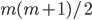 to be square,
to be square, 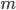 and
and 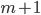 must have the property that the odd one is a square, while the even one is twice a square.
must have the property that the odd one is a square, while the even one is twice a square.
Hence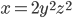 where
where 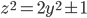 . This means, essentially that we want
. This means, essentially that we want 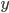 and
and 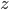 to be whole numbers such that their ratio is "as close as possible" to
to be whole numbers such that their ratio is "as close as possible" to 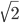 . We can now use the "continued fraction approximation" to
. We can now use the "continued fraction approximation" to 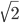 :
:
Truncating this expression at various places gives sequential candidates for the fraction
From there, if you work a little harder, you can derive the exact formulae for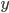 and
and 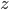 , which involves a piece which exponentially grows (proportional to
, which involves a piece which exponentially grows (proportional to 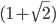 raised to some power) and a piece which exponentially shrinks (proportional to
raised to some power) and a piece which exponentially shrinks (proportional to 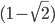 to some power). When you multiply everything together and expand it out, you end up with the formula I wrote down. But I can't be bothered to rederive it in detail right now!
to some power). When you multiply everything together and expand it out, you end up with the formula I wrote down. But I can't be bothered to rederive it in detail right now!
TY,
Goodness gracious, are you trying to make me sound like a crackpot? I just thought it was a pretty mathematical pattern! :-0
Your second comment seems right though....
Declan,
Not yet. These things generally involve a lot of time and deliberation. It's a waiting game now...
Aron,
Pretty neat, your mathematical reasoning to the final expression. And I didn't men to make you a modern day Nostradamus!
I'm not sure what it means, but I shoved the function into Desmos and discovered that the function on the left is a very little, tiny horizontal line on the horizontal axis that is bisected by the vertical axis.
-1.1x10^-16 </= n </= 1.1x10^-16
But I'm not sure what the right side of the equation means.
So, I concede that the problem is "above my pay grade."
Tim,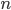 is an integer, this is the formula for the
is an integer, this is the formula for the 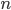 th number which is both square and triangular. The final output should always be an integer when
th number which is both square and triangular. The final output should always be an integer when 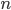 is an integer.
is an integer.
When
I'm not familiar with the graphing calculator you are using, but it may have been confused by the fact that if you insert a noninteger n, you may end up taking roots of a negative number (since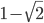 is negative). Also, the function increases exponentially, so for proper viewing it may be necessary to adjust the scaling of the horizontal and vertical axes.
is negative). Also, the function increases exponentially, so for proper viewing it may be necessary to adjust the scaling of the horizontal and vertical axes.