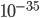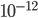Out with the Old Random Links

by Aron Wall Posted on January 1, 2019

Since it's now 2019, it's a good time to clear out some random links I've got bookmarked to show you.  Here they are:

♦  You can't take an introductory psychology course without hearing about Zimbardo's "Stanford Prison Experiment", but in fact many aspects were faked.  Part of the scam is that the experiment went so "badly" that it would be unethical for any other researchers to repeat it—but not so badly that it couldn't still be used to catapult himself to perpetual fame and glory.

♦  The hot new result in biology is "epigenetics", the idea that (modifying the standard Darwinian picture) the experiences of one generation can affect which genes are expressed in the next generation.  You'd never guess from the wild news coverage of this that the phenomenon has never been convincingly demonstrated in human beings.

♦  Martin Gardner's attack on Karl Popper.

♦  Llamas, the secret bioweapon for producing vaccines that work on all types of flu?  I'm putting a question mark on this, only because 90% of the amazing news stories about medicine don't pan out somehow.  I wish journalists would write more news stories about the things researchers discovered 10 years ago that are now definitely curing lots of people...

♦  Potoooooooo, a famous race horse and stud.  Pronounced POT-EIGHT-OHS.

♦  Rithomachy, the medieval arithmetic battle board game, was apparently nearly as popular as Chess for a few centuries.

♦  An illustrated history of the American Revolution by a Japanese book in 1861... in which the Founding Fathers battle various giant beasts.

♦  Bitcoin is currently using half a percent of the world's electricity.  Perhaps we shouldn't be squandering the planet's resources on a mindless race to manufacture currency that doesn't actually produce anything valuable?

[UPDATE 2/7/19: here's a possible rebuttal of the guy whose blog apparently started this ecological alarm.  Haven't put in enough work to figure out who's right here, but until then I'm taking these articles with a grain of salt.    If anyone knows more about this I'd be grateful if they weigh in.]

♦  In other cryptocurrency news: The (arguably unconstitutionally appointed) Acting Attorney General was previously involved in a scam to try to trick people into buying time travel cryptocurrency.  Unbelievable!  As if an AG disbelieving in Marbury vs. #@*$^&! Madison weren't bad enough.  (I knew about the UConn crackpot from when I decided not to apply to a faculty position there, but I had no idea these threads were connected...)  Apparently it really is important to educate the public about why time travel is worth talking about but not really worth investing your retirement savings in.

♦  The Sabbath as a radical act of protest against being treated as a slave by the economic system.

♦  The Graphing Calculator Story, another radical act of protest... in favor of voluntarily working without pay?  Hilarious.

♦  As for involuntary servitude, a cynical take on schooling: Part I, Part II.  As a lazy bright kid who didn't do most of the homework I was assigned despite significant feelings of guilt, I 100% endorse these posts (except I disagree with the bit opposing standardized tests, and have some reservations about the section labelled "foreign kids").

♦  Why state educational ratings are measuring the wrong thing.  As a libertarian magazine, Reason has its own biases, but it seems quite reasonable that we should control for different state populations, and shouldn't count money spent on education (which is a cost) as if it were an educational outcome (a benefit).  Don't forget to click on the plot that shows their new rankings.

♦  How the US Educational system does math word problems completely wrong, by a mathematician from Russia.  Come on, folks!

♦  I've heard several times before that there are different potentially valid models of how to look at mental illness, but I think a few paragraphs in the middle of this blog post give a particularly striking answer for what makes a "spiritual model" different from other approaches, namely that it actually engages with—even when it does not agree with—the content of mental issues in a way other approaches do not.  (I don't have any reason to think the author is a Christian, but I still found this helpful.)

Oh, and Ivy League schools should stop discouraging people from being supportive to students with mental illnesses!

♦  This account of fixing an issue causing depression is also somewhat interesting, although I'm not sure how well the method would work on everybody...

♦  St. Shamus Young has an interesting series about procedural world-building that I think is pretty cool; his autobiography/conversion-story is also worth reading through.  Not for the slow of connections, though.

♦  An interview with a Christian neuroscientist at Stanford, St. William Newsome.

♦  Here's a brain viewer that's supposed to show you how different parts of the brain are mapped out, but I'm not sure my own brain is capable of handling the web interface.  Let me know if anyone figures out how to actually extract useful information from this.

♦  A side effect of people becoming less religious is we start treating political cults as if they were a religious identity.

♦  St. Ben Sasse, Senator from Nebraska and St. John's College graduate, had some balanced remarks about the MeToo movement during the recent confirmation fight.

♦  Tips for more productive and realistic political conversations.

♦  The Believing Game, another conversational tool for identifying certain sorts of truths.

♦  A while back I gave some advice about how to read the Bible.  The same guy also asked about Church History, and I put off answering because I thought I might write a whole blog post on the subject.  Ha!  My actual recommendation is to start by reading The Lion Handbook on the History of Christianity.  Then, if you are curious about some particular great Christian of the past, find a translation and start reading their work for yourself.  If it doesn't speak to you, pick something else.

♦  You know how in the Bible, when the king Jeroboam split Israel off from the southern kingdom of Judah, he set up an alternative system of worship involving a sycretistic hybrid religion where YHWH was worshipped in the form of golden calves?  [If the answer is no, click on the first link in the previous item.]  Well, archaeologists have recently found a payrus with some creepy alternative psalms from the Northern Kingdom religion.  Although there are parallels to the Biblical Psalms, in these psalms YHWH is worshipped alongside other Middle Eastern Gods, and may be identified with a "Bull".  He is also portrayed as being satiated by bowls of sacrificial blood.  I think most Christians don't realize how a lot of the biblical Psalms (like #50) are polemics against this sort of crass religion.

♦  One of my ancestors, the Rev. Aron Wall, helped lead a group of Mennonites from the Ukraine to the United States.  I'm staring right now at a photograph of him and his wife that is hanging on our mantelpiece, and he looks almost exactly the same as in the photograph I just linked to.  The Mennonites weren't originally from the Ukraine either; as Anabaptists (the more radical wing of the Reformation) they had been persecuted by both Protestant and Catholic countries in Central Europe.

♦  The Biodeterminist Guide to Parenting, by popular blogger Scott Alexander, one of the few people I trust to summarize the actual scientific evidence in a suitably tongue-in-cheek manner.

♦  Recently I've been commenting sometimes on Scott's blog Slate Star Codex.  Readers of this blog may be interested in my Ask Me Anything which mostly turned into an argument about the evidence for Christianity.

I've also been having some interesting conversations with a guy who is summarizing the beliefs of secular biblical critics about the Bible; this spans many threads but you can find most of them by tracing back links from the index post for the Torah /"Deuteronomistic History", the index post for the Prophets, and the most recent post of his ongoing series on the Writings [I may update this with the Index post later.] You can find out why scholars believe the Documentary Hypothesis, and more about why I'm skeptical of such hypotheses.

Have a blessed 2019, everyone!

Posted in Links | 6 Comments

Breakthrough Panel Discussion on Time Travel

by Aron Wall Posted on November 7, 2018

Everyone seemed to love the panel discussion on "Is time travel possible?", featuring Veritasium's Derek Muller as host; and Nima Arkani-Hamed, Daniel Harlow, Daniel Jafferis, and myself as panelists. We had a lot of fun with it, but also there's some profound physics involved, in what one might have thought was a pretty flippant choice of topic. So without further ado, here it is:

(Back up to 7:55 if you want to hear all the introductions to the event at the beginning.)

After our panel there were two others on "What are the limits of Science" and "Is there life in the Universe", recorded in the same video. There were a lot of interesting people on these panels, although I don't think the conversations cohered quite as well as ours did, perhaps because they involved people from different disciplines.

In the second panel, Andrei Linde is a fun speaker, but I think he overplayed how much we currently know for sure about the early universe after inflation happened. There are a lot of mysteries between the time inflation ended (about 10^{-35} seconds after the Big Bang by his reckoning) and the time of the Higgs Phase Transition (about 10^{-12} seconds, which corresponds to the highest energy scale we can measure at the LHC). Between these times there are a lot of mysteries, like what process produced more matter than antimatter, as needed for any matter to exist today. I also wish he'd mentioned Cosmic Variance, a pretty obvious Limit on Science in his field.

Gary Ruvkin, the guy who thinks life on earth came from outer space was also kind of interesting. Apparently after about a billion years of nothing, life shows up on Earth and it's already pretty complicated. So maybe it came from elsewhere? The downside of this hypothesis, he said wittily, is that it "only buys you another 10 billion years" to evolve life (going back to the Big Bang). Since this is a physics and theology blog, I'll mention that even though I generally think that Darwinian evolution suffices to explain the evolution of complex life from simpler life, it does seem bewildering how something as complicated as the first cell might have arisen naturally, without a miracle. But just because I can't imagine it doesn't necessarily mean it couldn't have happened by some natural process. As a theist I am philosophically open to both supernatural and natural explanations, both of which are ultimately due to the Creator of all things.

That third panel should really have been: "Is there other life in the Universe", otherwise I think the question is pretty easy. This panel includes Jocelyn Bell Burnell who received a special Breakthrough prize this year for her revolutionary discovery of pulsars. Scandalously, the Nobel was given to her advisor but not to her; either because of sexism, or because of a bias against graduate students, or some combination thereof.

This seems like a good time to mention that, if I understand the history correctly, it was Daniel Jafferis' grad student Ping Gao who had the original idea to try to make a traversable wormhole in AdS/CFT. (Although as the 3rd person to join the collaboration, I can't speak to the exact division of labor between Ping and Dan.) Now the New Horizons prize was awarded for our lifetime of work so far, and not just for this one article, so I'm not saying that Ping should have been eligible for this particular prize. But I do think it's important for people to acknowledge junior collaborators, and not just assume the senior people did all the best work. So thanks Ping!

[Apparently I misunderstood the history, and is was Daniel who had the original idea and assigned it to Ping as a project.  I apologize for the mistake, but of course I'm still grateful to Ping for his hard work and insights!]

Posted in Physics, Talks | 5 Comments

Prizes

by Aron Wall Posted on November 4, 2018

I've recently won a pretty big prize in theoretical physics, called the New Horizons Prize.  This is a smaller version of the Breakthrough Prize which is awarded to more junior researchers.

My prize is shared with MIT's Daniel Harlow and Harvard's Daniel Jafferis, both of them excellent physicists.   Amusingly, each pair of us have written exactly 1 article together (but we have never collaborated as a trio).

I hope it is not too vain to share some news articles about the prize, in case people want to know more:

There is also going to be a prize ceremony today [i.e. the day I am writing this post], Sunday Nov 4th, in Mountain View.  You can find more information about the broadcasting of the event, and the other prize winners, here.  There will also be an all-day symposium at UC Berkeley this Monday, at which I will be getting the actual trophy and also we will be speaking at a panel on whether time travel is possible.  You can watch it live streamed here.

I've also recently received the 2018 Philippe Meyer Prize and the IUPAP Young Scientist Prize [alt link], both of whose award ceremonies will be in the future.

After all this shameless self-promotion, I have some even better news that makes me even prouder: in January Nicole and I are expecting our first child, a son!  We are so pleased by this, and hope that he will find this world hospitable as God's will is accomplished in his life.  I don't feel prepared yet to be a father, but then again no one ever is.  I understand that children are very good at training up their parents, so hopefully it will turn out all right!

Posted in Blog, Education, Physics | 10 Comments

How the Trump Administration Harms People I Know

by Aron Wall Posted on October 23, 2018

A few news cycles ago, everyone was discussing the Trump administration's cruel policy of separating migrant children from their parents (and then losing track of them, which cannot be anyone's ideal of efficient government).  This is a serious issue which deserved significant press coverage.  And a major campaign promise by Trump, to temporarily ban Muslims from entering the US, has resulted in a controversial executive order that was eventually upheld by the Supreme Court as constitutional (even though I'm sure many of the Justices would have struck down a similarly tainted domestic policy had the government not said it was related to "national security".)

However, in this post I want to talk about some more minor ways in which Trump's anti-immigration policies have hurt people I care about.  None of these people have suffered anything as extreme as the asylum-seeking families detained at the border.  But I think it is still important to talk about the lesser ways in which anti-immigrant policies hurt people, especially when I can speak from the experience of people I know personally.

There is a tendency for controversial, hot-button issues to soak up all the public attention.  Because of this, the public debate surrounding immigration usually focusses on illegal immigrants.  But the people I am going to talk about are legal immigrants, whom the government welcomed in, and is now treating badly.

(I will therefore not be discussing specifically the Iranian physicists negatively affected by the so-called "Muslim ban", even though I do know some individuals who have likely been negatively affected.  In my experience, none of the Iranians living in the US support the Iranian regime.)

As a fairly privileged upper-middle class person, it's fairly rare for political issues to affect me directly, except insofar as they contribute to my tax bill, and to the government grant monies that have sometimes paid my salary.  I have strong opinions about many of the issues involved, but as far as my life was concerned, the Obama administration was not much different from the Bush administration, except that it changed which news stories I read about on the internet.  So when people I actually know have their lives derailed by politics, I start paying attention!

The information below was obtained by conversations with the victims of these policies.  I assume their information is largely accurate, but I have not tried to check it with independent research.

I. Graduating Students

As you might expect, Stanford University accepts many bright graduate students.  This year, several of the High Energy students have defended their Ph.D.'s and graduated.  They had applied for prestigious postdoc positions starting this Fall, and were accepted.  These are some of the brightest students in the whole world, and they want to contribute their intellectual talent to our nation.

Unfortunately, because some of them are foreigners, from scary countries like China and Canada, rather than US citizens, they are required to get work visas.  In previous administrations, that involved some annoying requirements, such as a rule that you had to go back to your home country and apply from there.  The Trump administration, however, currently has a backlog of around 6 months processing all visas in this category.  Hence they have been unable to start their new jobs yet, even though the academic year started months ago.  During this time, they are:

- forbidden from gaining any income in the United States,
- unable to leave the country or return home, for fear of not being readmitted to the USA, and making their application less likely to be accepted.  (Despite the fact that they are here legally due to their previous visa.)
- advised against moving to their new location for fear of being held to be "working" for their new employer
- advised against doing research (which for us theorists is literally just "thinking/talking about physics") for the same reasons.

Graduate students are not very likely to be sitting on an enormous stash of savings, so this is obviously a serious issue for these students.  Imagine if the government told you that you are forbidden to work, and on top of that threatened you with dire consequences if you wanted to move back in with your parents, or move to any other country that did allow you to work for them.  I reckon you would be pretty upset.

So why didn't they just apply for their visa 6 months in advance?  Well, because any application submitted more than 3 months in advance is automatically rejected as being filed to early.  So yes, the Trump Administration is, by underhanded delay tactics, imposing a Catch-22 that makes it literally impossible for these students to start their new job at the beginning of the new academic year.

Since there are statutory quotas for the total number of people admitted, I'm not sure this foot-dragging will even have the effect of lowering the number of foreign workers in the USA.  It is just being jerks for no good reason, to the international people that we were going to hire anyway.

II. A Recent Faculty Hire

What about people higher up the academic ladder?  I was just hearing last night from a condensed matter theorist around my age, who was recently hired for a tenure-track position at a top UC school in his field.  (While there is some subjective element to this judgement, and he is a friend of mine, on almost any view we are talking about one of the top 10 most promising people in his subfield in the whole world.  That's how good you have to be to be hired at a place like that.)

While he is allowed to work, the backlog for him getting a Green Card (permanent residency) is currently 20 years!  Bear in mind, his employment already puts him in the highest priority category you can possibly get by virtue of employment.  (He could only do better if he was marrying a US Citizen or was a religious worker.)

Why so long?  Well, in its infinite wisdom, the government has decided there should be an equal number of spots for immigrants from every country, irrespective of the population of the country.  As if they were voting on Senators.  So people from India or China have difficulties, whereas somebody from a small Pacific island nation somewhere has no problems.  This is obviously stupid, but past administrations have remedied this by reassigning unused spots from countries like Liechtenstein to the nationalities with higher demand, while still staying under the total national quota.  Well, they aren't doing that any more.

So this guy, one of the most talented physicists in the world, with a permanent academic appointment, needs to wait two decades (or more likely, until a Democrat retakes the White House) just to be able to be a permanent resident.  In the meantime:

- he is ineligible for many grants
- he cannot return to India to visit his family, without having to go through an extensive, 3 month background check on return (and possibly being denied re-entry).
- his brother wanted to visit him but was denied a tourist visa (due to his age bracket and being from India; however his parents were able to visit him).

III. What God Says

The Bible teaches that we are to treat foreigners fairly and not to oppress or harass them.  This is a major theme in Old Testament, starting with the Torah:

Do not oppress a foreigner; you yourselves know how it feels to be foreigners, because you were foreigners in Egypt.  (Ex 23:9, cf. 22:21)

When a foreigner resides among you in your land, do not mistreat them.  The foreigner residing among you must be treated as your native-born.  Love them as yourself, for you were foreigners in Egypt.  I am the Lord your God.  (Lev 19:33-34)

The Law required foreigners to be given full access to justice:

Do not deprive the foreigner or the fatherless of justice, or take the cloak of the widow as a pledge.  Remember that you were slaves in Egypt and the Lord your God redeemed you from there. That is why I command you to do this.  (Deut 24:17-18)

The Levites shall recite to all the people of Israel in a loud voice...

“Cursed is anyone who withholds justice from the foreigner, the fatherless or the widow.”

Then all the people shall say, “Amen!”  (Deut 27:14,19)

This included provision for refugees escaping from oppression in other countries:

If a slave has taken refuge with you, do not hand them over to their master.  Let them live among you wherever they like and in whatever town they choose. Do not oppress them.  (Deut 23:15-16)

and for both private and public welfare systems for those who fell down on their luck:

When you reap the harvest of your land, do not reap to the very edges of your field or gather the gleanings of your harvest.  Do not go over your vineyard a second time or pick up the grapes that have fallen. Leave them for the poor and the foreigner. I am the Lord your God.  (Lev 19:9-10, cf. 23:22)

When you are harvesting in your field and you overlook a sheaf, do not go back to get it. Leave it for the foreigner, the fatherless and the widow, so that the Lord your God may bless you in all the work of your hands.  When you beat the olives from your trees, do not go over the branches a second time.  Leave what remains for the foreigner, the fatherless and the widow.  When you harvest the grapes in your vineyard, do not go over the vines again.  Leave what remains for the foreigner, the fatherless and the widow.  Remember that you were slaves in Egypt.  That is why I command you to do this.  (Deut 24:19-22)

At the end of every three years, bring all the tithes of that year’s produce and store it in your towns,so that the Levites (who have no allotment or inheritance of their own) and the foreigners, the fatherless and the widows who live in your towns may come and eat and be satisfied, and so that the Lord your God may bless you in all the work of your hands.  (Deut 14:28-29, cf. 26:12)

as well as a commandment making it illegal to discriminate against immigrants:

You are to have the same law for the foreigner and the native-born. I am the Lord your God.  (Lev 24:22)

 For the generations to come, whenever a foreigner or anyone else living among you presents a food offering as an aroma pleasing to the Lord, they must do exactly as you do.  The community is to have the same rules for you and for the foreigner residing among you; this is a lasting ordinance for the generations to come.  You and the foreigner shall be the same before the Lord: The same laws and regulations will apply both to you and to the foreigner residing among you.  (Num 14:6)

although this general principle presumably did not take precedence over other Torah commandments which explicitly treated foreigners differently in specific respects, e.g. the rule against charging interest in Deut 23:19-20 applied only to fellow Jews, not to foreigners.

Of course, the message of welcoming strangers continues with the Prophets and the New Testament, but this is enough to make my point.

IV My Own Opinion

Now I am well aware that the United States of America is not a theocracy like ancient Israel, and that there are plenty of laws in the Torah which it would be inappropriate to enforce (or even follow) in modern day conditions.  But as a Christian, I believe that there are ethical principles to be found in the Bible which I ought to pay attention to.  Charity towards foreigners is one such ethical principle, and it is flouted by so-called Christian "conservatives" who idolatrously say "America First!" instead of putting God first.

Not that I accept for a minute that the immigrants I know are bad for America.  Our scientific preeminence requires us to recruit top talent from around the entire world, to stay on top.  I oppose trying to reserve academic positions for Americans for the same reason I'm not a fan of affirmative action, because I believe that it's best for jobs to be filled by a merit based system without regard to extraneous factors.  If that means that we get a lot of Indian and Chinese people, good for them!  A bunch of geniuses are coming from all over the world wanting to work for us, and somehow that's a bad thing?  It's not like you can just hire some random guy who lost his auto manufacturing or coal mining job.

There is also an enormous humanitarian good to be gained by allowing more people into developed First World countries.  However, I do not believe that the US should have completely open borders.  First, because I think there are valid national security reasons to keep terrorists and other undesirable criminals out.  Secondly, because there may be a maximum rate of immigrants that we can accept without overburdening our society or culture.

Still, there has never been a wealthier society than ours, capable of meeting more people's needs.  Nor has there been any society with a stronger track record of assimilating immigrants successfully.  And pretty much all economists on either side of the political aisle agree that protectionism in trade is bad for both countries.  It's almost a mathematical theorem.

But even if you believe differently than me about these broader issues, it's not like the policy makes sense for any of the academic people I mentioned above.   If the government had legitimate national security concerns about any of them (which would be frankly absurd, given the people in question), they shouldn't have let them into the country in the first place.  There's no way that it's in our national interest to let people into the country, lavish our educational resources on them, and (eventually) decide they can stay, but jerk them around the whole time, and make the process a bureaucratic nightmare.

Posted in Ethics, Politics | 28 Comments

The Image of God

by Aron Wall Posted on October 16, 2018

Imagine an art historian whose life work is to study Picasso paintings.  She analyses the minute flecks of paint on each work, to determine their composition.  She also goes to conferences where people divide the paintings into different eras, and tries to see if her results can be related to their discoveries.

However, she doesn't believe Picasso actually existed.  Nor do most of her colleagues.  A few of them do, but it is considered somewhat gauche to mention it in talks or official publications.

It's a bit like this whenever a scientist doesn't believe in God.  The work may have technical expertise, even brilliance, but it misses the forest for the trees.  It is blind to the biggest, most important result of all.

I don't mean to imply that Atheism is as implausible as Picasso-denial would be.  The philosophical arguments for the existence of God require careful contemplation, and some thoughtful individuals have resisted them as (in their opinion) fallacious.  Indeed, most scientists don't give the question careful thought at all.  But as somebody who is convinced God exists, the final outcome still seems (regardless of how understandable it may be) a little bit comic or absurd.  You may not believe in God, but you carefully study his laws and decrees.  Look up from your work, contemplate the ocean or hills, and ask your heart where all this beauty came from!

There is yet another respect in which God haunts Science, as its inspiration and origin.  We can also look at the scientist as a human being.  Without the human mind, Nature would of course still exist, but Science (which is just the careful study of Nature by beings with minds) would not.

Jews and Christians believe that all human beings — no exceptions! — are created in the image of God.  It is because we have a likeness to the Creator, that we are capable of both Science (understanding God's creation) and Art (making our own creations).  So scientists who don't believe in God aren't just blind to what's in front of them, they are also blind to their own true self, to the spiritual power that enables them to work on a calculation or a measurement.  But, their work still reflects God's glory, even though they don't recognize it.

Now God is invisible.  As the Creator, God precedes Nature and transcends it.  Divinity has no physical form, and the human mind cannot comprehend it.  To make a graven image of any animal or person, and worship that as if it were divine, is regarded in the Bible as idolatry, a serious sin.  Yet this same book insists from its very first chapter that God created men and women in his own image!

The human animal may be a rather Picasso-esque, surreal representation of the uncreated, bodiless, singular Power that set the stars in the sky and binds quarks into nuclei; yet it is the representation that is given to us, as a handle to reach out and touch the divine.  We are not God, but we are like God; and by serving our neighbor we also serve the one who made him.

And although none of us yet fully live up to our potential as icons or paintings of God, we have the promise that the Master Artist is working on us, striving forcefully to mold us into that perfect image (if only we allow ourselves to be worked on).  We are all broken in many ways, and that definitely includes me!  But the same God who patiently waited billions of years to make our world — who brought forth the evolution of single cells, sponges, fish, dinosaurs, and (in these last days) birds — is also working to redeem each of us, and the human family as a whole.  That is why Christ came to earth, on a daring rescue mission: to put us back in touch with the source of the whole universe.

This is far more exciting and interesting than the shallow sentiments that most moderns try to console themselves with.  As St. Dorothy Sayers observed, "There was never anything so perilous or so exciting as orthodoxy, nothing so sane and so thrilling."  In that respect it is, again, like the best moments of scientific discovery.

Posted in Theology | 15 Comments