A few years ago I wrote a series of blog posts (starting here) discussing the debate between Sean Carroll and St. William Lane Craig.
Well, last week I was invited to St Cameron Beruzzi's internet show Capturing Christianity, along with fellow guests Sts. Luke Barnes and Ronald Cram, to give further comments about the debate.
You can still watch it by following this link. The whole thing is about 2 1/2 hours long.
Here is an excellent blog post St. Brandon Watson about how to fix the system that leads to police brutality. My own reflections follow:
There is a long history of racist policing in the United States. It is natural to assume that if the problem involves racism, the best solution must necessarily be to make a change that directly addresses racial issues. However, often the solution to a problem can only be found by thinking more generally than the original problem.
A better solution (and one that might have a chance of success without immediately turning the issue into an intractable argument) is to make structural changes that increase everyone's rights and protections against arbitrary actions by police and others.
I'm sure that the majority of police officers are decent people who would not approve of going around murdering people, but the fact is if you give to some class of individuals what effectively amounts to the power of life-and-death over ordinary citizens, it only takes a small minority of abusive individuals to lead to serious problems. That is why those who are entrusted with great power must also be held to a higher standard of responsibility.
Racism will indeed influence which communities and individuals are targeted by the police (although the extent to which specific aspects of the policing system are racially biased is a complicated sociological question without clear-cut answers). But our goal here should not merely be to make it so that summary executions without trial are fairly distributed between different ethnic groups. The goal should be to make it so that nobody in America believes themselves to have the legal power to execute unarmed and helpless captives without a trial (I'm not talking about how the police should respond to armed assailants, which is a different matter where judgment calls are unavoidable).
The only way to make that happen is to provide consequences for people who do such things. And one way to try to implement that is by revisiting legal doctrines such as qualified immunity, which stack the deck in favor of government officials who violate people's rights.
A couple of readers have asked for my take on the Pandemic.
1. First of all, practical matters: If you haven't already been told a hundred times already, you should try to avoid going to places with people in them, besides members of your own household (assuming none of them are sick yet!). This is our way of protecting, not only ourselves, but elderly and sick people.
Some have questioned whether shutting down the economy will lead to even worse consequences than the disease itself. Certainly, this is going to lead to suffering for many poor people and small business owners and workers. But while nobody knows all of the effects of such decisions, in the short run suspending the inessential parts of the economy probably actually saves lives on net (even before taking into account stopping the disease!), what with less driving cars, and less pollution.
Maybe we can take this opportunity to remind ourselves that what we call the "economy" often reflects priorities that are not completely healthy and beneficial? Just as an individual can benefit from a period of fasting from inessential luxuries, to learn what is more important, a whole society can benefit from a fast as well.
These days there are services in most places to order groceries online and have them delivered to your door. If you can still find time slots available, that is much safer than going to the grocery store yourself. (There is some chance of getting exposed to the virus from touching surfaces, e.g. food packaging, but people breathing droplets is thought to be the main way it spreads. If you are concerned about viruses on surfaces you can wash the outer packaging in soapy water, as we have been doing.)
If you have frozen or imperishable food stored up, you can also eat that.
You can also order delivery from restaurants, if needed. This is less ideal, but at least this way at most 1 person from outside breathes on you per meal.
If none of those strategies works for you, then you might still have to go to the store, but please do so as infrequently as you can (which means you should try to make each trip count, by buying enough food for say 2 weeks if possible). Wear a mask if you can, or at least cloth over your face.
If you are in a vulnerable demographic, maybe you could get somebody else to go to the store for you? If you are healthy, perhaps you could provide this service for someone who is not?
If you are living in a house with a sick person, of course make sure their needs are met, but do your best to try to minimize your exposure to their germs. Infection is not just a yes/no thing—it turns out that the quantities of virus you are exposed to matter. If you are exposed to only a small number, it takes the viruses longer to reproduce to dangerous numbers, giving your immune system more time to crack their code and build up antibodies.
2. But what about the theological significance? In each generation, there is a temptation for Christians to read too much into the disasters of that time as if they were some unique sign, rather than the way life is in general.
Is the Pandemic a sign of the End Times? Should we expect Jesus to be coming back any moment now? Well, it seems like the Black Death (which killed a lot more people) would have been an even stronger sign, and we know that Jesus didn't come back in the 1300's. Even the Spanish Flu probably killed more people per capita than Covid-19 will.
Let's see what Jesus says, in the beginning of his discourse to his disciples about the End Times, which—going by the chronology of Holy Week in the Gospel of Mark—he probably preached on the Tuesday before he was crucified (so this blog post is 1 day late, sorry!).
From Matthew 24 [with the two words in brackets taken from the parallel passage in Luke 21]
While He was sitting on the Mount of Olives, the disciples approached Him privately and said, “Tell us, when will these things happen? And what is the sign of Your coming and of the end of the age?”
Then Jesus replied to them: “Watch out that no one deceives you. For many will come in My name, saying, ‘I am the Messiah,’ and they will deceive many: You are going to hear of wars and rumors of wars. See that you are not alarmed, because these things must take place, but the end is not yet. For nation will rise up against nation, and kingdom against kingdom. There will be famines and earthquakes [and plagues] in various places. All these events are the beginning of birth pains. Then they will hand you over for persecution, and they will kill you. You will be hated by all nations because of My name.”
Note the words I have highlighted here. The words in red involve various types of human conflicts (often leading to bloodshed), the words in blue involve natural disasters (including plagues like Covid-19), and the words in black indicate what Jesus says about both of these categories: Don't panic, this is what happens in each generation, it is not any kind of indicator that you live in the last generation. It is not the end, it is just the beginning.
Jesus does, however, refer to these signs (which manifest to different degrees in every generation of human history), as the "birth pains", so he doesn't entirely reject the idea of looking at them as some sort of "sign".
Actually, Covid-19 is a sign of the End Times, but only in a certain sense. It is not the sort of sign that silly prognosticators are looking for, who—in defiance of Jesus' statement that not even angels, or the Son with respect to his human knows the day or hour, but only the Father—try to predict the time of the End. Rather, it is a sign for the wise, for those who know how to interpret events.
Let's compare it to tooth decay. When I was 28, I had to get my wisdom teeth removed; they had actually grown in perfectly fine, but they were decaying since I hadn't kept them as clean as I should have. The dentist said they'd need to be removed or else crowned, and even that would only hold for another decade or so. So I had them taken out—but that's another story.
Covid-19 is a sign of the mortality of the human existence as a whole, in exactly the same way that tooth decay is a sign of your own mortality. A wise man will learn from such experiences the frailty of his mortal condition, and will recognize from it the inevitability of his eventual physical demise. But, that does not mean that you'll be hit by a bus the moment you walk out of the doctor's office on painkiller, nor does it mean that you can use cavities as a sort of guidepost to predict the year and manner of your death. True, an untreated tooth abscess might well be the thing that kills you, but most likely you'll be done in by something completely different.
3. As I said, many Christians have a temptation to interpret recent historical events as if they were a lucid story where we can read off the plot and say what the moral is. (Scholars sometimes call this sort of tendency, Historicism.) We can be sure that historical events fulfill God's will, but it is hubris to think, in the absence of specific revelation about the matter, that we can give a detailed explanation of how or why they do so.
Let us turn to the favorite book of the prognosticators: the Book of Revelation. Near the beginning of the book, John has a vision of God in heaven, and in that vision he sees a strange sight:
Then I saw in the right hand of him who sat on the throne a scroll with writing on both sides and sealed with seven seals. And I saw a mighty angel proclaiming in a loud voice, “Who is worthy to break the seals and open the scroll?” But no one in heaven or on earth or under the earth could open the scroll or even look inside it. I wept and wept because no one was found who was worthy to open the scroll or look inside. (Rev. 5:1-4)
The scroll that is full of writing represents the hidden meaning of God's creation. If there is a Creator, and if he created human beings for a purpose, then this hidden significance has to exist! But it turns out that nobody is worthy—smart enough or good enough or holy enough—to penetrate the depths of this mystery.
As Ecclesiastes says: "He has made everything beautiful in its time. He has also set eternity in the human heart; yet no one can fathom what God has done from beginning to end." This mystery, represented here by the "seven seals", is a problem for those who try to defend God by constructing plausible theodicies.
True, any idiot can see that it is sometimes true that suffering builds character, that freedom requires the possibility of bad choices, and that great good can sometimes come out of terrible evil. And if there is an afterlife, we cannot expect that our final fulfillment will come in this life, but rather we are being prepared for another (and unimaginable) state of existence.
But for precisely this reason, those who seek to come up with facile philosophical explanations of exactly why God allowed this war or that disease, in a way that is supposed to be more satisfying then repeating such obvious platitudes, are fooling themselves. As Housman wrote:
"Malt does more than Milton can
To justify God's ways to man."
Does that mean that there is no way to understand the purpose of Creation? Not quite, since there is one who knows:
Then one of the elders said to me, “Do not weep! See, the Lion of the tribe of Judah, the Root of David, has triumphed. He is able to open the scroll and its seven seals.”
Then I saw a Lamb, looking as if it had been slain, standing at the center of the throne, encircled by the four living creatures and the elders. The Lamb had seven horns and seven eyes, which are the seven spirits of God sent out into all the earth. He went and took the scroll from the right hand of him who sat on the throne. And when he had taken it, the four living creatures and the twenty-four elders fell down before the Lamb. Each one had a harp and they were holding golden bowls full of incense, which are the prayers of God’s people. And they sang a new song, saying:
“You are worthy to take the scroll and to open its seals,
because you were slain,
and with your blood you purchased for God
persons from every tribe and language and people and nation.
You have made them to be a kingdom and priests to serve our God,
and they will reign on the earth.” (v. 5:5-10)
The slain Lamb, of course, represents Jesus, and his sacrifice on the Cross. At the Cross, and only at the Cross, God's hidden purpose for human suffering and agony become apparent. Hence, only the risen Jesus is fully worthy to interpret the meaning of human history, and in particular whatever suffering the sick may be experiencing right now.
To the extent that we can have a glimmer of this now, as a person other than the Savior, it can only be to the extent that we meditate on the Cruciform love of God that was revealed there, and let it permeate our thoughts and character. This is nothing more nor less nor other than the call to fully become a saint. To become a saint is to have a satisfactory resolution to the Problem of Evil, in a particular life. But the gate is open for that person only. The next person to come along will not be able to grasp the explanation, unless they too are on the road to holiness.
As the Lamb begins to open the Seals one by one, John sees the famous "Four Horsemen of the Apocalypse"—but originally the term "Apocalypse" just meant the four Horsemen that appear in the Apocalypse of John, i.e. the Book of Revelation. (Although, they were first seen by the Prophet Zechariah.) The woes they bring are the same as the ones that Jesus described at the start of the Olivet discourse, and which have characterized every era of human history: conquest, war, famine, and pestilence.
I watched as the Lamb opened the first of the seven seals. Then I heard one of the four living creatures say in a voice like thunder, “Come!” I looked, and there before me was a white horse! Its rider held a bow, and he was given a crown, and he rode out as a conqueror bent on conquest.
In the 20th century alone, about 100-200 million people were killed as a more or less direct consequence of government policy (e.g. genocide and deliberate starvation), not counting military deaths. (This is based on old notes for a Sunday school class; I'm not going to try to find all my sources again.)
When the Lamb opened the second seal, I heard the second living creature say, “Come!” Then another horse came out, a fiery red one. Its rider was given power to take peace from the earth and to make people kill each other. To him was given a large sword.
About 40 million people were killed in battle in the 20th century.
When the Lamb opened the third seal, I heard the third living creature say, “Come!” I looked, and there before me was a black horse! Its rider was holding a pair of scales in his hand. Then I heard what sounded like a voice among the four living creatures, saying, “Two pounds of wheat for a day’s wages,and six pounds of barley for a day’s wages, and do not damage the oil and the wine!”
Famine was responsible for the deaths of about 70 million in the 20th century.
When the Lamb opened the fourth seal, I heard the voice of the fourth living creature say, “Come!” I looked, and there before me was a pale horse! Its rider was named Death, and Hades was following close behind him. They were given power over a fourth of the earth to kill by sword, famine and plague, and by the wild beasts of the earth. (v. 6:1-7)
Death seems somewhat redundant with the effects of the previous Horsemen. Indeed, Death seems to get pretty much everyone eventually. Even if we only focus on the new element of infectious disease, this one is actually MUCH bigger than the other 3. In the 20th century, around 200 million people were killed by smallpox alone, and that was just one of many deadly scourges.
Most of the deaths by plague in the 20th century came near the start. As a result of vaccines and better medical care, death by infectious disease dropped in developed countries (e.g. the USA) to only about a 10% the rate it had before. Even with the novel coronavirus running rampant, we live in very sheltered times compared to every other era in human history!
The 5th Seal is also something common through many eras:
When he opened the fifth seal, I saw under the altar the souls of those who had been slain because of the word of God and the testimony they had maintained. They called out in a loud voice, “How long, Sovereign Lord, holy and true, until you judge the inhabitants of the earth and avenge our blood?” Then each of them was given a white robe, and they were told to wait a little longer, until the full number of their fellow servants, their brothers were killed just as they had been.
In the 20th century there were, depending on how you count, somewhere around 45 million Christian martyrs.
Only when we reach the 6th Seal to we seem to get imagery that corresponds to the actual End Times, and it seems to comes in a huge spectacle all at once:
I watched as he opened the sixth seal. There was a great earthquake. The sun turned black like sackcloth made of goat hair, the whole moon turned blood red, and the stars in the sky fell to earth, as figs drop from a fig tree when shaken by a strong wind. The heavens receded like a scroll being rolled up, and every mountain and island was removed from its place.
Then the kings of the earth, the princes, the generals, the rich, the mighty, and everyone else, both slave and free, hid in caves and among the rocks of the mountains. They called to the mountains and the rocks, “Fall on us and hide us from the face of him who sits on the throne and from the wrath of the Lamb! For the great day of their wrath has come, and who can withstand it?”
I expect that this provides us with a picture of the Second Coming which is at least as literal as the Book's depiction of the body of Jesus (a Lamb with 7 eyes and 7 horns). Yes, Christ will return to Earth just as he has promised, but John's vision was not given to him to satisfy all of our curiosity about exactly how it will happen.
In my opinion it is more profitable to meditate on the deep irony inherent in the strange and paradoxical phrase "Wrath of the Lamb". This is a rather astonishing juxtaposition. A lamb is not an animal that most people would associate with apocalyptic rage and judgement. What can this mean?
It means that when God arrives to forcibly overthrow all the powers of the world, he will do so with the same body that suffered on Earth as a meek, innocent victim of torture and execution. A person who—although he was very far from being a physical or verbal doormat—told his disciples not to resist their persecutors, and who willingly forgave his tormenters. That person, and nobody else, is going to finally end all violence and disease, and economic exploitation, and religious oppression. Not by beating them in a fair fight on their own terms, but rather by the sheer power and glory and worthiness of his unveiled and crucified divinity.
This blog post will not attempt to interpret the strange Sabbath rest of the 7th Seal. Nor will I attempt to give an interpretation of the Trumpets and Bowls which follow the Seals in the text (although this does not necessarily imply anything about their chronological order) except to note the obvious fact, that depending on how the future unfolds, the human race could easily face severe ecological devastation as a result of human sin and mismanagement of the Earth.
The main purpose of these visions and teachings is not to show us what we have to suffer—there has always been plenty of that on Earth, even without special Tribulations and Persecutions—but rather to show us who suffered along side us.
Those of us who persist in reading the Scriptures, or the events of our lives, with the goal of finding Jesus there, will not I think find them to be without meaning.
6. How long was it between the time when the supposed supernatural events took place, and when they were first written down (in a document that has had copies of it preserved). Is it early enough to suggest the text is based on testimony rather than later legends?
Last time, we looked at the ancient religions of Hinduism and Judaism, which make claims about events taking place long enough ago, that there is room to doubt or deny the very existence of their foundational figures. But even in the case of founders who clearly existed in historical times, there is often a significant gap of centuries between the time they lived, and the time in which the accounts (or legends) about them were written down.
(This particular post will not focus on religious founders during the modern era, e.g. Joseph Smith, for whom lots of contemporary documentation still exists. Modern founders can usually pass this test fairly easily, although in many cases the contemporary material is sufficiently embarrassing that these religions might have been more plausible if less contemporary material had been preserved...)
Pali Canon (gap of centuries)
I'm no expert on Buddhism, but I gather that the earliest texts seem to have been written down quite a long time after his death. First of all, Buddhist traditions can't even agree on which century Gautama Buddha lived in; some traditions say 563-480 BC, others say 483-400 BC. (Although, if you think that's bad, the scholars can't even agree on which millennium Zoroaster lived in!)
According to Gautama's Wikipedia article:
Various collections of teachings attributed to him were passed down by oral tradition and first committed to writing about 400 years later.
although the article on the Pali canon (the earliest collection of Buddhist scriptures, compiled by Theravada tradition) suggests that a few of the books may have been fixed by the reign of Ashoka (268-232 BC).
Because these are some of the earliest documents we have about Buddhism, in the other parts of this series I will be implicitly assuming that the Pali canon contains a more or less authentic account of Buddha's teachings. But it should be kept in mind that we still have them at a significant remove.
This is a significantly longer period of time for legends and accretions to develop, compared to the interval of 20-30 years between e.g. Jesus' Resurrection and St. Paul's letters.
Lotus Sutra (more centuries, also snake people)
Other Buddhist texts were written much later still, and have no good claim whatsoever to be based on the life of the historical Buddha. For example, one of the most popular Buddhist religious texts outside the Pali canon, the Lotus Sutra of the Mahayana tradition, teaches the inspirational doctrine that anyone who seeks Enlightenment can eventually become another Buddha, helping others in turn. This text has the following origin story.
The tradition in Mahayana states that the sutras were written down during the life of the Buddha and stored for five hundred years in a nāga-realm [i.e. a parallel world populated by snake gods]. After this, they were reintroduced into the human realm at the time of the Fourth Buddhist Council in Kashmir.
which hardly inspires confidence that the text really represents the authentic teachings of the historical Gautama Buddha. (Would you trust a snake-person to accurately copy a manuscript?) It takes only a small modicum of skepticism to suspect that this document was actually written around the time of its supposed "reintroduction to the human realm", which if the above account is correct would have taken place c. 78 AD or c. 127 AD depending on when Emperor Knishka took the throne, approximately 5 or 6 centuries after the death of Buddha).
If my argument in the previous installment was right, the fact that the Lotus Sutra is legendary should also be pretty obvious from its contents and style, since it is very hard to spin convincing fake histories out of whole cloth. Let's see if this suspicion bears out.
This text opens with the Buddha surrounded by (if I've looked up the terms correctly) over 12,000 fully enlightened monks, 8,000 additional monks and nuns, 80,000 irreversibly enlightened bodhisattvas, 42,000 heavenly deities of various kinds, hundreds of thousands of snake-gods, millions of horse-headed deities, bird-headed deities, nature spirits of different kinds, and oh, a few hundred thousand normal humans too. (One wonders who was doing the catering for this event?) At this time, the Buddha emits a ray of light from his forehead that illuminates the entire multiverse. The crowds then listen to him expound his teaching of the sutra for 60 small kalpa [i.e. aeons lasting billions of years], before he passes into Nirvana.
It is hard to take this seriously as the recording of a historical event. To be very clear, my reason for saying this is not that the text contains a supernatural event. (The Bible also contains supernatural events.) Nor is the problem that the supernatural events described contradict my Christian worldview. (That would be circular reasoning, if we are trying to figure out whose religion is most plausible.) Rather, the problem is that the text makes no attempt whatsoever to fit the supernatural events into a plausible historical narrative that fits within the space and time parameters of the historical Siddhartha Gautama's life, the monastic teacher who lived for 83 years (not billions of years), during which the population of India probably did not include millions of people with animal heads, at least according to our current archaeological understanding.
Thus, it's not so much that the Lotus Sutra tries to be historically plausible, but fails to be fully convincing due to a few minor slip-ups about details. As far as historical accuracy goes, this document is not even competing in the same tournament as the canonical Gospels! Given its legendary nature, any spiritual value it has can only survive if the text is capable of standing on its own independently, apart from being historically grounded in the words of the actual Buddha. But for this particular text, I don't see how that can work very well, since a lot of the content of the Lotus Sutra consists of specific promises supposedly made by the Buddha to his disciples, on the basis of his preternatural wisdom. If the Buddha didn't actually make these promises, then what reason do we have to trust them?
(To Christians, the Lotus Sutra is also noteworthy in that it contains an alternative version of the parable of the Prodigal Son. Because of the greater complexity of the Buddhist story, my personal opinion is that the Christian version probably came first; not that it matters much theologically, because we already know that Jesus sometimes adapted illustrations from other sources. The Buddhist version of the tale is notably different though, in that the father only becomes wealthy after the son departs. Also, in the Buddhist version the son really is taken on as a hired servant; not because of any defect in the father's love, but rather because the son is skeptical that the rich man is actually his father, so the father devises it as a clever scheme to gradually entrust the son with more and more privileges, so as to eventually restore the relationship.)
The Miracles of Zoroaster (gap of millennia)
With regard to the miracles of Zoroaster, the (non-religious) Encyclopædia Iranica says:
These miracles do not reflect historical events; they are always associated with the mythical and legendary history of Mazdaism and the ancient Iranian epic, although the miracle itself remains, as in other cultures, an act contrary to the laws of nature or one attributable to divine intervention (Sigal, p. 10). One might even say that there is no hagiography in Iran comparable to that which grew up in Christendom or in Islam. Even though Zoroaster can be considered a saint, the legends concerning his life and miraculous deeds are probably of late origin. They are not comparable to the miracles attributed to Jesus and his disciples, nor indeed to those attributed to Christians martyred under the Sasanians (see Gignoux, 2000). The invention of miracles in Mazdaism may be the result of competition towards the end of the Sasanian period with other established religions (i.e., Judaism, Christianity, and Islam), the aim perhaps being to show the holiness and eminence of the founder of Zoroastrianism; such hagiographic traditions can scarcely have survived for more than a millenium...
The sources concerning Zoroaster... and others are Dēnkard V and VII, the Wizīdagīhā ī Zādspram (see ZĀDSPRAM), and the Wizīrkard ī dēnīg. No historic accounts exist of the life of Zoroaster. The Mazdean theologians formulated pious legends, mainly based on their own imaginative perceptions, although one may surmise the existence of lost parts of the Avesta or the Zand that would have attested them. The existence of many variations between the texts may be construed as evidence of their authenticity, or merely an indication that there was competition to relate the most striking and demonstrative miracles. [bolded emphasis mine.]
Of the three sources mentioned above: the Zadspram dates to the 9th century AD; the Denkard dates to the 10th century AD; and the Wizīrkard ī dēnīg has an extremely controversial and convoluted textual history. Although the story of Zarathustra’s life is narrated by Medyomah in the first person, the transmission of the manuscript can only be traced back to 1239 AD (and even this date is controversial, since when the text was published in 1848 it was rejected and suppressed, leading to the destruction of most copies of the text).
To summarize this data: Zoroaster died somewhere in the range 1500 - 600 BC. The earliest accounts of his miracles seem to date to the 800-1200's AD, which is approximately two thousand years later, in texts that written during the dominance of Christianity and Islam, when Zoroastrians needed to show that their religious founder was just as cool as those other religious founders. In this case the gap is too large to take the claims seriously.
The Oral Torah (a millenium and a half)
Rabbinic Judaism also has some relatively unconvincing claims of oral transmission from the past. It claims that its interpretations of the Torah (which are compiled in the Talmud, the first layer of which was written down c. 200 AD) are based on an unwritten "oral torah" given by God to Moses himself, more than fifteen centuries earlier. Even though we have no records of anyone talking about the oral torah before about 150 BC, when the party of Pharisees began to exist! This is staggeringly implausible, not just because of the lack of references in the written Torah to this supposed secret tradition, but also because of the tumultuous history of the Jews described in the Bible, during which the written Torah barely survived intact.
(Incidentally, Jesus was vehemently opposed to these oral traditions of the Pharisees, even though in other respects his theology was in closer agreement with the Pharisees than the other Jewish sects of the time. After the destruction of the Temple, the Pharisees and Christians were the two main sects of Judaism that survived. Although in medieval times, there was a significant sect of Jews who rejected the oral torah, called the Karaites.)
Orthodox Jews believe that the Great Sanhedrin (i.e. the supreme council of 71 rabbis who judged the most important religious cases, which existed until 358 AD), goes back all the way to the time of Moses. The Torah does say that there were 70 elders who received the Holy Spirit at the time of Moses, but there is no statement that this was intended to be a permanent body, nor are there any references to the Sanhedrin before 76 BC. Prior to the Babylonian Exile in 605 BC, decisions about the law seem to have been normally rendered by priests, not by rabbis (who did not exist before the Exile, and who therefore also do not have an unbroken chain of ordination going back to Moses).
The New Testament (decades)
In the case of the New Testament, the exact dating of the Gospels is somewhat controversial, but it is pretty uncontroversial to say that they are all products of 1st century Christianity, which places them no more than 70 years after the death of Jesus c. 33 AD. (Some unusually skeptical scholars date the Gospel of John to the early 2nd century, say 110 AD, but I believe this is currently a minority opinion.)
I personally think the Gospels were probably written significantly earlier than this. For example, one of the main reasons these scholars date the Synoptic Gospels to after c. 70 AD, is that in them Jesus predicts the destruction of the Temple at Jerusalem, about 40 years before it happened. But this argument seems to rest on the anti-supernaturalist assumption (sometimes called "Methodological Naturalism") that historians should never accept supernatural explanations on principle. These scholars are basically asking the question: "Given the premise that predictive prophecy is impossible and that Christ didn't really say this, when did this text most likely arise?" But that would be circular reasoning, if we are trying to decide which if any religion is believable in the first place!
(Sure, if a scholar has other reasons to believe Christianity is false, it would be completely rational for them to ask what historical conclusions would follow from that. But the scholarly constructions of such hypothetical scenarios, are almost always presented to the public as if they were a refutation of Christianity based on definite historical evidence, instead of what it almost always is: a speculative historical reconstruction based on the assumption that Christianity is wrong.)
Without such biased assumptions, it is just as plausible to suppose that the Synoptic Gospels were written more like 30 years after the death of Jesus, and the Gospel of John perhaps another decade or two after that. Especially if the Gospels were actually written by their traditional authors Matthew, Mark, Luke, and John, as testified to by nearly all subsequent Christian writings to discuss the question, beginning in the 2nd century. Earlier dates are also suggested by the kind of indicators of historicity I described last time.
One can argue for a more conservative point of view as follows: The book of Acts (a text in the New Testament describing the early history of the Christian Church) highlights the missionary work of Sts. Peter and Paul, but strangely ends at an anticlimax (St. Paul is in Rome awaiting trial, but hasn't yet been tried by Caesar or executed). One can think of several possible explanations for this omission, but the simplest one is that these events hadn't happened yet. This would put Acts in the early 60's at the latest. But Acts is a sequel to the Gospel of Luke (by the same author), and Luke's Gospel is generally believed to have used Mark as one of its sources. This would probably push Mark back to the 50's AD, i.e. less than 30 years after the Crucifixion of Jesus. (I don't claim that this argument from silence is completely watertight, not at all; but the arguments for later dates are at least equally indirect and circumstantial. What's sauce for the goose is sauce for the gander.)
To a young person, a few decades may seem like a long time—but actually this is really good by the standards of most ancient historical texts. It means that the New Testament was written down when at least some of the people who had witnessed the key events were still alive. Similarly, most scholars of ancient literature would probably kill to get multiple sources identifying the author of their favorite text from the century after it was written.
On the other hand, the surviving Gnostic Gospels were all written much later, mostly in the 2nd-4th centuries. A possible exception is the Gospel of Thomas, which could be from the 1st century, but is more usually dated to the 2nd.
The letters by St. Paul are dated (depending on the letter) in the interval between the late 40's and his martyrdom in the early 60's. Secular scholars generally think only about half of the 13 Pauline epistles in the New Testament were actually written by him (opening the door to later dates for the rest of them). I would dispute this judgment, but it is not of great importance in this context, since the most important letters from the point of view of Christian apologetics mostly belong to the undisputed category. (Although if 1 Timothy is authentic, it would give another reason to date the Gospel of Luke earlier than Paul's death, since 1 Tim 5:18 appears to quote from Luke as if it were already authoritative Scripture.)
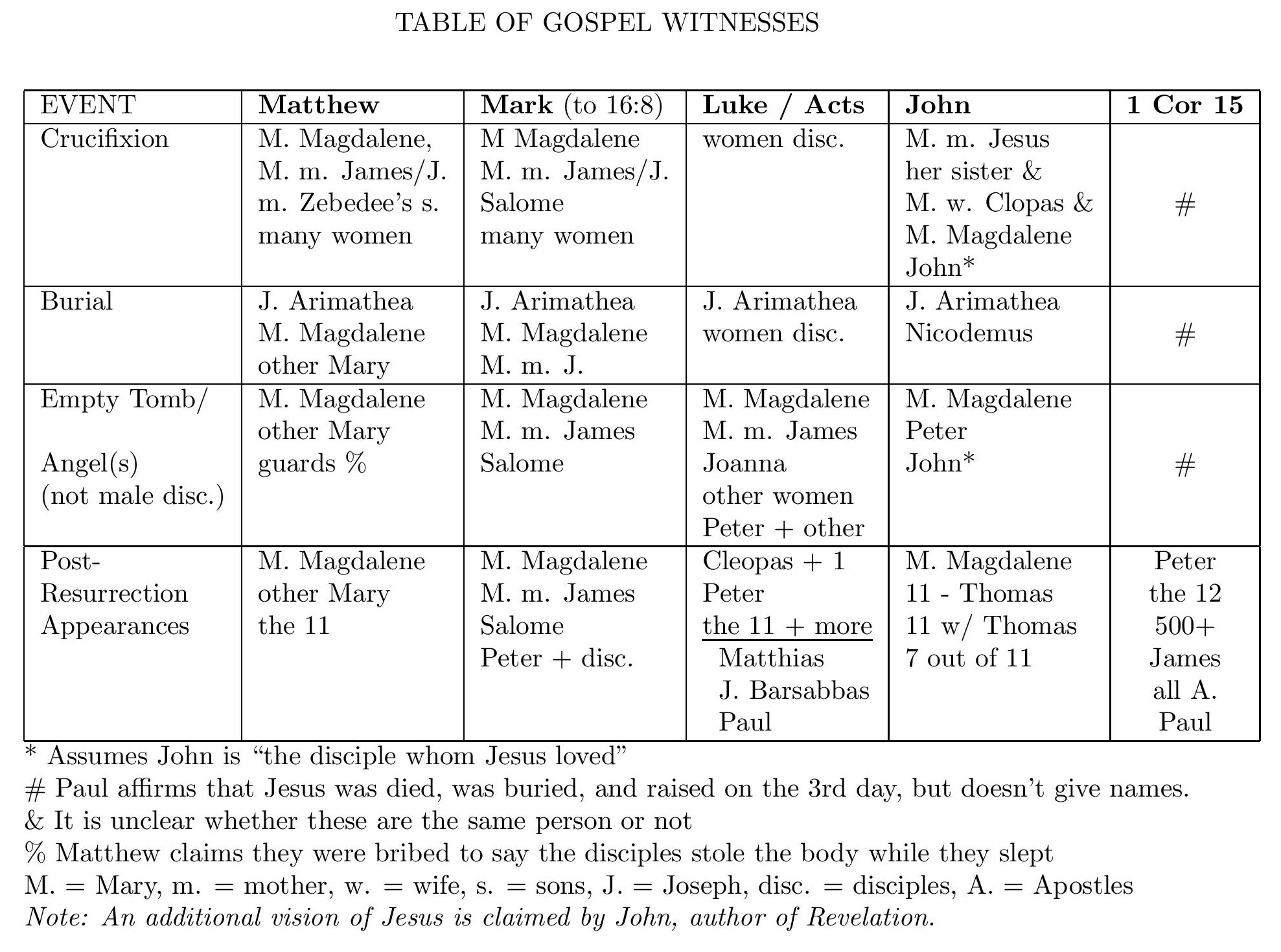
One particularly important passage (in a letter that is undisputedly by St. Paul himself) recites a long list of eyewitnesses to the Resurrection of Jesus:
For what I received I passed on to you as of first importance: that Christ died for our sins according to the Scriptures, that he was buried, that he was raised on the third day according to the Scriptures, and that he appeared to Cephas [i.e. Peter], and then to the Twelve. After that, he appeared to more than five hundred of the brothers at the same time, most of whom are still living, though some have fallen asleep. Then he appeared to James, then to all the apostles, and last of all he appeared to me also, as to one abnormally born. For I am the least of the apostles and do not even deserve to be called an apostle, because I persecuted the church of God. But by the grace of God I am what I am, and his grace to me was not without effect. No, I worked harder than all of them—yet not I, but the grace of God that was with me. Whether, then, it is I or they, this is what we preach, and this is what you believed. (1 Cor. 15:3-11)
By cross-referencing Paul's ministry to other historical events, this letter is usually dated c. 55 AD, that is about 25 years or so after the claimed appearances. It implies that St. Paul was given a list of individuals and groups who encountered the resurrected Jesus before he himself did (although he omits the women who were the first to see Jesus, possibly because the ancient world, being sexist, did not take the testimony of women as seriously).
To get more detailed information about what actually happened during several of these appearances, you have to read the Gospels or Acts. (No one source gives all of the Resurrection Appearances, but several Appearances seem to be described by multiple sources.) This data is summarized in a table at the end of this post.
A Note about my Methodology
I'd like to make a slight digression about my methodology at this post, in order to highlight at least one potentially biasing factor in my own research.
In the last section I questioned the anti-supernaturalist assumptions of biblical critics. But I only know about these circular assumptions because I've investigated the Christian religion closely enough to have my own opinions.
On the other hand, for most of the other religions in this section like Buddhism, I have had to rely on the dates given by supposedly objective "neutral" scholarship as summarized by e.g. Wikipedia. On the other hand, I would never rely on the supposedly "neutral" scholarship on Wikipedia in the case of Christianity, which I consider to be tainted by its deference to secular biblical scholarship. So is this a fair mode of proceeding?
Well, one possible answer is this: given my current level of knowledge of other religions I don't see much alternative, so it will have to do for now. But if anyone is aware of evidence that other religious texts are dated in a way which is also cynical and biased against the claims in question, they are welcome to present this evidence in the comments.
And I do think I am able to reject similarly specious rejections of religious histories when I encounter them in the wild. For example Patricia Crone, a highly respected Islamic Studies scholar at the IAS, seriously argued that Mohammad never really lived in Mecca. This is exactly the kind of bizarre reinterpretation of Islamic history which I would never accept in the case of Christianity, and indeed I don't accept it for Islam either!
Also, even if I were to take the views of secular biblical critics at face value, the gap before the New Testament was written down would still compare very favorably to all of the cases reviewed above, where the record gap is much longer. (The large majority of secular biblical scholars date the Gospel of Mark to c. 70, which is still only four decades after the death of Christ, i.e. within the lifespan of a single individual. And this document is filled with lots of different miracles.) So I think an apples-to-apples comparison still ends up with Christianity coming out looking very favorably on this point, compared to other ancient religions.
(By the way, I don't think my rejection of manuscripts that were supposedly preserved by snake-people in a parallel universe, or manuscripts written on golden plates that are invisible almost all the time, counts as a similarly pernicious methodological assumption. There's a big difference between: 1. being open-minded enough to potentially accept manuscript evidence for supernatural claims if the texts bear the marks of being actual historical documents, and 2. being so gullible that you'll accept documents written by people who basically said to their contemporaries: "No, you can't see the previous manuscripts, they were invisible the whole time because of this additional supernatural event, an event which makes it so this totally isn't a situation where I just wrote this document right now and tried to pass it off as a lot older than it actually is".)
The Quran (effectively contemporaneous)
We now turn to the most recent of the large world religions. According to Islam, the primary source of religious knowledge is the Quran (supplemented by traditions called Hadith, see below). The Quran itself was extensively memorized by a large number of people, and written down not very long after Mohammad's death.
The evidence does not seem to support the extravagant claim by orthodox Muslims that the Quran was preserved perfectly, since there is plenty of evidence for variant readings among early Muslims. (Mohammad is said to have explained some of the variant readings among different Muslim groups by claiming that the Quran had been revealed in 7 different Arabic dialects, but this could easily have been an ex post facto rationalization in order to keep peace in the community.) Also, the third caliph Uthman ordered the destruction of all versions of the Quran except a standardized edition, thus removing most of the evidence of early variations. From a scholarly perspective, this is the worst possible way to make the exact contents of the text certain.
Nevertheless, the Quran was likely still preserved with a very high degree of accuracy, due to the large number of listeners who memorized, recorded, and preserved it. So I think we can trust that the version we have today is extremely close to the words that Mohammad himself spoke. Thus, for the practical purpose of deciding whether Islam is true, I think we can take the text of the Quran for granted as being nearly identical to the version spoken by Mohammad.
(As stated in the last section, I am assuming that the standard outline of Muslim history reported by Muslims is basically accurate in its broad outlines, and there are no giant conspiracies to make up entire cities and dynasties during the period after Mohammad. Which is not to say that there are no legends or exaggerations, or that facts are not recounted from a specific viewpoint. I think this is entirely reasonable and fair, given the number of people involved and the fact that it was founded during historical times. I don't think weird revisionist theories of early Islam should be taken seriously, any more than weird revisionist theories of early Christianity.)
So far, so good. However, the purpose of this exercise was to assess the credibility of specific supernatural claims, not merely to assess the evidence for the mere historical existence of the religion itself at the time of its supposed founding.
And for the most part, the Quran itself doesn't record any miracles actually done by Mohammad. In fact there are a great many disavowals of the miraculous, in which he explicitly refuses to perform miracles! (On occasion, the Gospels also record Jesus refusing to perform miraculous signs to convince skeptics, yet there are far more incidents described where Jesus does perform dramatic miracles, usually out of compassion for suffering people, and often in the presence of his enemies.)
There are three noteworthy exceptions:
(1) The Night Journey in which Mohammad was taken from Mecca to Jerusalem, described for example in the following verse:
Exalted is He who took His Servant by night from al-Masjid al-Haram to al-Masjid al-Aqsa, whose surroundings We have blessed, to show him of Our signs. Indeed, He is the Hearing, the Seeing. (Sura 17:1)
Later traditions (not found in the Quran) say that the journey took place on the heavenly steed Buraq, and that in his journey Mohammad also ascended to Heaven, where he met with a series of previous prophets. Suspiciously, no one on Earth witnessed any of this besides Mohammad himself, so mostly we are left with his bare claim to have done this.
(2) The Splitting of the Moon is mentioned in just 2 consecutive verses of the Quran:
The Hour has come near, and the moon has split. And if they see a miracle, they turn away and say, "Passing magic." (Sura 54:1-2)
If it weren't for later traditions (see below), it wouldn't be 100% clear that this is supposed to be a sign at the time of Mohammad's ministry (a few Islamic commentators have thought that this text refers to a sign that will take place in the End Times).
(3) The primary miracle of Islam is supposed to be the literary beauty and inimitability of the Quran. This has always seemed unconvincing to me as a supernatural sign, since there have been many other brilliant poets in history with rough backgrounds. And as far as I can judge personally from English translations, while parts of the Quran certainly have a forceful grandeur (e.g. the magnificent Rolling Up Sura), taken as a whole I do not get the same impression of stylistic beauty that I get from many other poetic books.
Admittedly, I don't know what it's like in the original Arabic. (I was never very good with foreign languages, so I'm not going to try to learn it either.) Most Muslims would say that this doesn't fully count as reading it, and I can certainly believe that it sounds far better in the original.
But this is yet another way in which Islam, despite its attempt at universalism, is much more bound to a particular culture than Christianity is. We accept translations of the Bible in all languages, because Christ is for everyone! And while no translation can capture all of the stylistic features of the original, quite a bit of the poetic beauty of e.g. the Psalms and Isaiah comes through just fine in English translations.
Hadith (a couple centuries)
There are also several reports in the Hadith (later oral traditions about Mohammad's words and deeds) that Mohammad did miracles. Now, the major collections of hadith were not written down until a couple centuries after Mohammad's death, and there are typically several people in the chain between the first person who wrote it down and the prophet. So far this may not sound all that impressive...
...but on the other hand, many of these traditions are recorded by multiple lines of transmission. For a few hadith, there are so many independent chains of transmission that it is essentially impossible for a reasonable person to doubt their validity. For other hadith, there is only a single chain of transmission, so you have to decide whether you think that the narrators were trustworthy. Muslim hadith scholars have taken great pains to try to separate out the reliable from the unreliable hadiths, by checking the accuracy of all the individuals responsible at each step of the chain of transmission (although in Sunni Islam, the Companions of Mohammad himself are pretty much just axiomatically assumed to be reliable, which is potentially problematic for those who do not already accept Islam). In many ways, their minimal threshold for accepting hadith as reliable are quite impressive—if also somewhat legalistic and rigid.
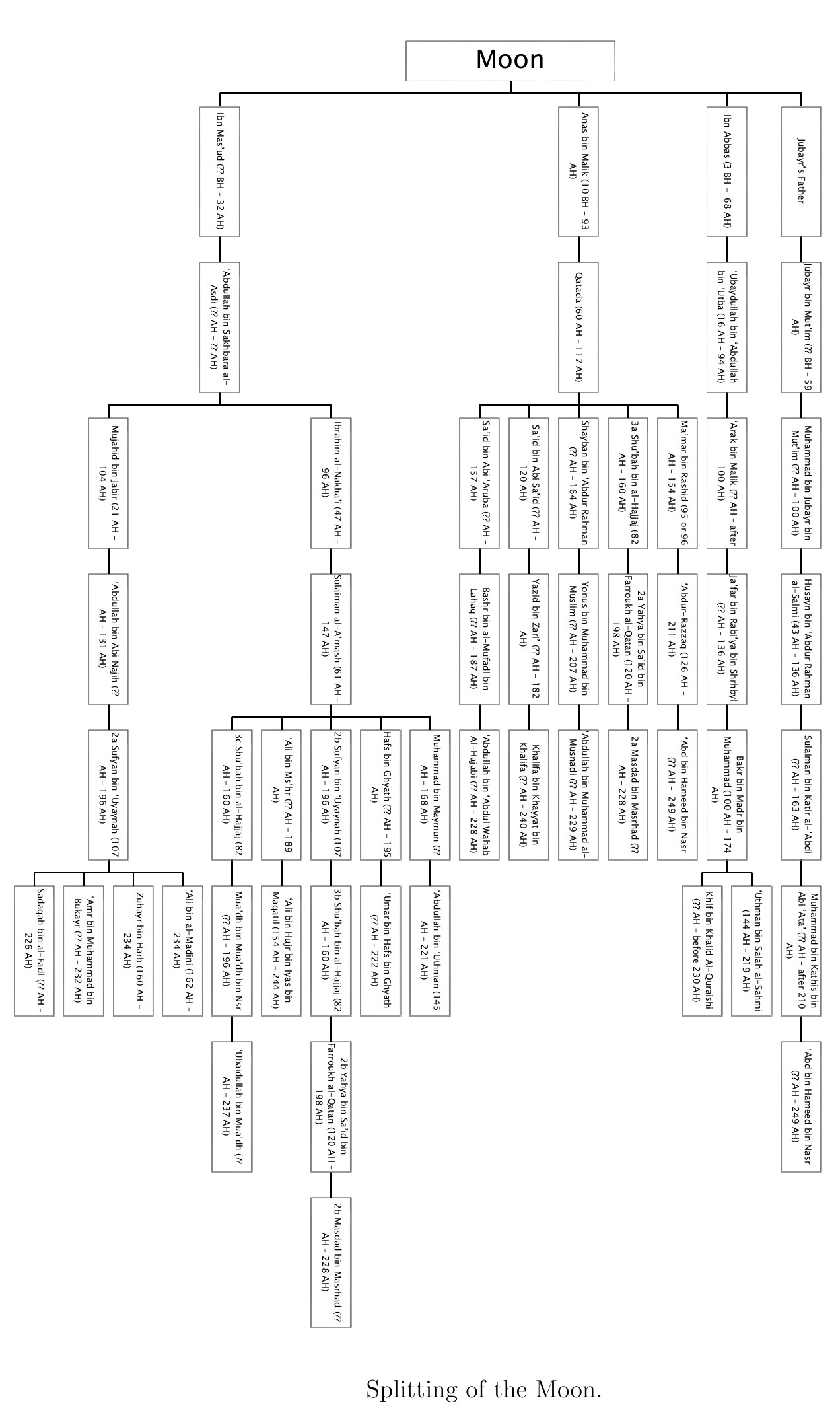
At the end of this post I will insert a "tree diagram" showing the chain of transmission for the hadith for the Splitting of the Moon, which is one of several miracles attributed to Mohammad in Hadith.
Comparison between Christian and Islamic miracle sourcing
While the 2nd century testimony for e.g. the authorship of the Gospels is quite good by the standards of ancient history (when it comes to nonbiblical texts, scholars are willing to accept authorship claims with far less evidence), as an apologist I can only wish that the early Christians put as much attention into explicitly recording chains of transmission as the early Muslims did.
On the other hand, there was also less need for them to do so. The writers of the Gospels and Acts were writing within a few decades of the events they wanted to record, and—operating within the usual conventions of Greco-Roman biography—they found it sufficient to merely name some of the individuals who were present at each event, with the implication (normally unstated) that some of these individuals were sources for the historian. What we are really seeing here is the distinction between a literate culture and an oral culture.
Since the Gospels were preserved in an essentially fixed form before the first generation of witnesses had died out, there was not the same need to construct elaborate chains of transmission, when the written documents came from the Apostles themselves or their close associates.
So I don't think that the miracle reports in the hadith can be casually ruled out as later legends. But that does not mean I am willing to concede that these miracles actually happened. (See the next question).
In order to facilitate a head-to-head comparison between the Resurrection of Jesus (the most important Christian miracle) and the Splitting of the Moon (which I consider the most impressive Islamic miracle of those that are well-attested), I include the following two charts, giving the witnesses associated with each miracle claim:
[I am grateful to my friend Ahmed for providing me with the following "tree diagram" illustrating the chains of transmission for the "Splitting of the Moon". The top 4 names are those who are claimed to be direct eyewitnesses of the miracle, while the bottom names are the last members of the chain, whose testimony was recorded in early, reputable hadith collections along with the chain of narrators]
Next: Natural Inexplicability
People were getting an error message when they tried to read the previous post:
Comparing Religions V: Historical Accounts
I've fixed the issue now, so if you weren't able to read this post before, you can do so now! (Although some people were probably able to read it before since it was correctly displayed on the main page of the blog)
It is also now possible to leave comments on that post, so feel free to write in complaining that I unfairly dismissed the historical evidence for Frodo, or whatever else you'd like to say.
