In the Valley of the Shadow of Death

by Scott Church Posted on October 3, 2021

A lesson from Martin Luther on walking in faith during pandemics.

By Scott Church – Guest Blogger

After decimating nearly one-third of Europe during the 14th Century, the Bubonic plague continued to ravage it in periodic epidemics before it was effectively eradicated in the mid-20th Century (White, 2014; Schiferl, 1983; Griggs, 2014). For the most part, these outbreaks were isolated to villages or regions, and it was possible to flee to safety elsewhere until they subsided. In August of 1527, one such outbreak came to Wittenberg while Martin Luther was at the university there, and Elector Johann Hess of Saxony ordered him and other professors to flee to Jena for safety.

Luther refused, choosing instead to stay behind with his wife Katharina von Bora and open their home as a ward for the sick, whom they cared for at great personal risk to themselves. He penned a letter to Elector Johann explaining his reasons (Luther, 2020). Five centuries later, in the age of COVID-19, his words and the testimony of his life show us what true God-fearing faith during pandemics is... and more importantly, what it is NOT.

In his words,

"[W]hoever serves the sick for the sake of God's gracious promise... has the great assurance that he shall in turn be cared for. God himself shall be his attendant and his physician, too. What an attendant he is! What a physician! Friend, what are all the physicians, apothecaries, and attendants in comparison to God? Should that not encourage one to go and serve a sick person, even though he might have as many contagious boils on him as hairs on his body, and though he might be bent double carrying a hundred plague-ridden bodies! ... Therefore, dear friends, let us not become so desperate as to desert our own whom we are duty-bound to help and flee in such a cowardly way from the terror of the devil, or allow him the joy of mocking us and vexing and distressing God and all his angels..."

True disciples don't deliberately put themselves in harm's way out of mere fealty to church doctrine, or to appease worldly narratives and political agendas others have tarnished it with for reasons that serve their own interests rather than God's. They do so in loving service to their neighbor. In the words of the apostle Paul, they offer themselves as living sacrifices, holy, acceptable to God, which is their reasonable service (Rom. 12:1).

Note the reference to reasonable service (from the KJV Bible)—Or as the Amplified Bible renders it, "rational (logical, intelligent) act of worship." Genuine faith sees the face of Jesus in the poor, the oppressed, and the sick, and with full rational knowledge of the risks involved, seeks to be His healing face in their lives. It is in THAT place that we trust God's Will for our best, and our neighbor's.

By contrast, Luther tells us, there are those who,

"Sin on the right hand. They are much too rash and reckless, tempting God and disregarding everything which might counteract death and the plague. They disdain the use of medicines; they do not avoid places and persons infected by the plague, but lightheartedly make sport of it and wish to prove how independent they are. They say that it is God's punishment; if he wants to protect them he can do so without medicines or our carefulness."

This sort of "faith" will have nothing to do with reason (logic, intelligence). It flies recklessly in the face of real-world facts, rejects medicine, makes no attempt to socially distance from the sick, and even goes so far as to make fun of those who do, simply to assert its independence... that is, freedom.

Sound familiar...?  ;-)

According to Luther,

“This is not trusting God but tempting him. God has created medicines and provided us with intelligence to guard and take good care of the body so that we can live in good health… If one makes no use of intelligence or medicine when he could do so without detriment to his neighbor, such a person injures his body and must beware lest he become a suicide in God's eyes. By the same reasoning a person might forego eating and drinking, clothing and shelter, and boldly proclaim his faith that if God wanted to preserve him from starvation and cold, he could do so without food and clothing. Actually that would be suicide.

It is even more shameful for a person to pay no heed to his own body and to fail to protect it against the plague the best he is able, and then to infect and poison others who might have remained alive if he had taken care of his body as he should have. He is thus responsible before God for his neighbor's death and is a murderer many times over. Indeed, such people behave as though a house were burning in the city and nobody were trying to put the fire out. Instead they give leeway to the flames so that the whole city is consumed, saying that if God so willed, he could save the city without water to quench the fire..."

True disciples are rational (logical, intelligent). They embrace science, medicine, and socially responsible behavior—not out of license masquerading as "freedom," but because they are responsible to God for their own health, and... [wait for it] ... their neighbor's. To do otherwise—to reject their reasonable service, which is holy, acceptable to God—is to tempt Him rather than trust Him, and in so doing, become a murderer plain and simple.

In summary, he tells us,

"No, my dear friends, that is no good. Use medicine; take potions which can help you; fumigate house, yard, and street; shun persons and places wherever your neighbor does not need your presence or has recovered, and act like a man who wants to help put out the burning city. What else is the epidemic but a fire which instead of consuming wood and straw devours life and body? You ought to think this way: Very well, by God's decree the enemy has sent us poison and deadly offal. Therefore I shall ask God mercifully to protect us. Then I shall fumigate, help purify the air, administer medicine, and take it. I shall avoid places and persons where my presence is not needed in order not to become contaminated and thus perchance infect and pollute others, and so cause their death as a result of my negligence. If God should wish to take me, he will surely find me and I have done what he has expected of me and so I am not responsible for either my own death or the death of others. If my neighbor needs me, however, I shall not avoid place or person but will go freely, as stated above. See, this is such a God-fearing faith because it is neither brash nor foolhardy and does not tempt God."

Nor is this restricted to personal faith only. It is a calling to the church and community as well,

“'Whoever loves danger,' says the wise man, 'will perish by it' (Ecclus. 3:26). If the people in a city were to show themselves bold in their faith when a neighbor's need so demands, and cautious when no emergency exists, and if everyone would help ward off contagion as best he can, then the death toll would indeed be moderate. But if some are too panicky and desert their neighbors in their plight, and if some are so foolish as not to take precautions but aggravate the contagion, then the devil has a heyday and many will die. On both counts this is a grievous offense to God and to man..."

To these ends, Luther’s exhortation to “make use of medicine and intelligence” is particularly timely for us. When diseases broke out in his world, one had only two options—do your best to avoid them; and pray for a healthy recovery if you don’t succeed. We, on the other hand, have been blessed with five centuries of advances in virology, immunology, and medicine his world didn’t have. And of all the blessings at our fingertips in the age of COVID-19, one stands out more than any other—the one that allows us to arm ourselves against it, and possibly even eradicate it… vaccines. Unfortunately, many people still aren’t getting them, which is keeping widespread herd immunity out of reach. In the United States in particular, many are flat-out refusing vaccination for ideological reasons, not the least of which is a general hostility toward science and public health measures that from all appearances, no amount of evidence or logic will ever be able to penetrate. Many others, however, are hesitant due to concerns about how safe and effective COVID vaccines are (especially considering public health recommendations to continue masking and social distancing even after vaccination) but can otherwise be reasoned with if these concerns are addressed. They can be.

COVID vaccines are effective

As of this writing, three COVID-19 vaccines are in general use in the United States: The messenger RNA-based (mRNA) vaccines manufactured by Pfizer and Moderna, and the Johnson & Johnson adenovirus-based "one-shot" vaccine. All three have been thoroughly tested and approved by the FDA (Tanne, 2020; Oliver, 2020). The AstraZeneca adenovirus-based vaccine has also been approved for general use in Europe (EMA, 2021). Demonstrated efficacies of mRNA-based vaccines against infection or symptoms requiring hospitalization from the original wild strains of SARS-COV-2 are 95-97% for the Pfizer–BioNTech BNT162b2, and 92-95% for Moderna mRNA-1273. Corresponding figures for the Johnson & Johnson [J&J] Ad26.COV2.S and AstraZeneca–Oxford ChAdOx1 nCov-19 vaccines are around 67-72% (Haas et. al., 2021; Tenforde et. al., 2021; Callaway, 2021; Noor, 2021; Polack et. al., 2020; Mahase, 2020; Olliaro et. al., 2021; Mallapaty & Callaway, 2021).

As of Sept. 2021, these figures are still holding up well, even against recent variants such as B.1.617.2, or Delta. Per multiple studies in Europe and North America, effectiveness of the Pfizer–BioNTech vaccine against the more robust and transmissible Delta variant ranges from 79% to 88% for infection and symptomatic illness, and 89% to 100% (!) for hospitalization (Tregoning et. al., 2021; Lopez Bernal et. al., 2021; Baraniuk, 2021; CDC, 2021).

For all vaccines collectively, one recent study in New York found overall age-adjusted effectiveness against new COVID-19 cases and hospitalizations to be 75% and 89.5% to 95.1% respectively (Rosenberg et. al., 2021). A similar recent study in England found 50-60% effectiveness against infection by Delta (symptomatic or otherwise), including the less effective one-shot ones such as J&J (Smout, 2021). Even a single immunization has been shown to boost neutralizing titers against all variants and SARS-CoV-1 by up to 1000-fold (Stamatatos et. al., 2021), and one study of new COVID-19 cases in Kentucky during May and June of 2021 found that those who were vaccinated were 2.34 times less likely to be infected than those who had previously had COVID-19 and survived but weren't vaccinated (Cavanaugh et. al., 2021). One recent study in Israel did find an effectiveness of only 64% for Pfizer–BioNTech BNT162b2 against infection and symptomatic illness (Hass et. al., 2021). However, it was based on incidence rates in subjects who were considered fully vaccinated one week after receiving their second dose, whereas per U.S. CDC guidelines, one isn't considered fully vaccinated until two weeks after their second dose (CDC, 2021b).

If one does contract COVID-19 after vaccination, severe symptoms, hospitalizations, and deaths among breakout cases are almost an order of magnitude lower than those among the unvaccinated. Even in the case of the more vaccine-resistant Delta variant, the Pfizer–BioNTech BNT162b2 and Moderna mRNA-1273 vaccines reduce risk of hospitalization after four months by 93% and 91% respectively, and by 92% and 77% after six months (Scobie et. al., 2021; Self et. al., 2021).

But of course, if in doubt one could simply check the trended data on new US cases and deaths vs. vaccination rates since mass distribution of these vaccines began in earnest last January (JHUM, 2021). The dramatic declines in COVID-19 with rising national vaccination levels reflected in these datasets are self-evident. The spike in new cases after July 11, 2021 was almost entirely due to the Delta variant spreading among the unvaccinated, who as of July 30, 2021 comprised 96-99.8% of all cases (Kates et. al., 2021). And among the rising percentages of breakthrough cases (thanks to the unvaccinated Petrie dish), severe illness, hospitalizations and deaths are clearly a fraction of those for the unvaccinated (CDC, 2021c; Evans & Wernau, 2021).

By the numbers and the extensiveness with which they've been tested, the effectiveness of these vaccines in preventing infection, hospitalization, or death from COVID-19 is beyond reasonable dispute. But that said, it's important to be clear about what we mean by effectiveness and efficacy (there's a difference). When we say, for instance, that the Pfizer–BioNTech vaccine has an efficacy of 88% against infection, we mean that in controlled studies where a random sample of subjects received the Pfizer vaccine and an identical (or as similar as possible) control group of subjects received a placebo, 88% fewer subjects in the vaccinated group contracted COVID-19 during the trial period than the unvaccinated group--that is, if 100 COVID-19 cases turned up in the unvaccinated group, twelve did in the vaccinated group, and likewise for efficacies against hospitalization and death. On the other hand, vaccine effectiveness generalizes these comparisons to wider vaccine use in the general public. Since vaccine distribution and use may differ regionally and/or demographically from controlled laboratory studies, vaccine effectiveness may differ somewhat from efficacy.

In both cases, what we are NOT saying is that an efficacy/effectiveness of 88% against infection means that vaccines only work for 88 out of 100 people, nor that they will only work 88% of the time for you. Likewise, 93% efficacy/effectiveness against hospitalization does NOT mean that seven out of every 100 breakout cases will be hospitalized, and the rest will be asymptomatic. It isn't hand grenades. :-)

It simply means that there will be 88% fewer infections and 93% fewer hospitalizations in a vaccinated population than an unvaccinated one. But everyone who is vaccinated still has some level of protection from vaccines that they wouldn’t otherwise have. [The WHO Vaccine efficacy, effectiveness and protection page has a very readable and informative overview of all this.]

All other factors held constant the bottom line is that vaccination protects everyone and does so in at least three ways.

First, while it is true that in some cases the individual protection offered by vaccines may not be enough to prevent one from coming down with the disease or being hospitalized, they still reduce everyone’s risk for infection, and nearly all of those who do come down with a breakout case anyway will have less severe symptoms than they otherwise would have. How well vaccination protects you personally will depend on a wide range of factors including your age, your overall immune function, any comorbidities you may have, how much exposure you get from daily life (home, workplace, etc.), and more. But regardless, you will be more protected with vaccination than without it. And unless you have known life-threatening vaccine allergies or related immune function risks, getting vaccinated poses no risk compared to remaining unvaccinated since you would have to be infected and get sick to generate an immune response anyway, so there's no reason not to get one.

Second, if 88 out of 100 people who are vaccinated don’t contract COVID-19 when exposed to it, that means there are 88 fewer people spreading the disease before they develop symptoms, which in turn reduces everyone’s risk of exposure to it in the first place (more on this shortly). This is a key point, especially for those who intend to love their neighbor as themselves…

Choosing to be vaccinated doesn’t just protect you from infection, it protects your loved ones, your friends, and your community.

Finally, and most alarmingly, the vast majority of people filling hospital beds nationwide and around the world are unvaccinated COVID-19 patients, and the resulting burden is taxing healthcare workers and resources to the breaking point—so much so that in many regions, hospitals are literally having to resort to “death panels” to decide who gets care based on their likelihood of survival (Knowles, 2021; Hiltzik, 2021; Westneat, 2021). In other words, we have now reached a point in this pandemic where people are literally dying from preventable conditions because there are no hospital beds for them.

A month ago, my 89-yr-old father fell and broke his knee. He was left on a gurney in a hallway at Deaconess Hospital in Spokane, Washington for eight hours because there wasn’t a single bed available for him—all but a handful were being used by unvaccinated COVID-19 patients from Idaho who were seeking care in Washington because of the very Idaho hospital death panels discussed in the last two sources cited above. If he’d been in a car accident, needed an emergency appendectomy, or had a heart attack, he’d be dead… for literally no reason other than that all the beds in the nearest hospital were taken up by unvaccinated COVID-19 patients.

Choosing to be vaccinated doesn’t just protect you from hospitalization and death, it protects doctors, nurses, and healthcare workers struggling to save lives, and saves everyone from needless crippling or death due to lack of available care.

COVID vaccines are safe

As of this writing, nearly 6.3 billion COVID-19 vaccinations have been administered worldwide. More than 393 million have been administered in the United States, and 63% of the U.S. population have had at least one shot (Ritchie et. al., 2021; JHUM, 2021). Anaphylaxis adverse reaction rates have run around 0.0011% for Pfizer and 0.00025% for Moderna or roughly two to eleven adverse events per million vaccinations administered (Rutkowski et. al., 2021; Shimabukuro et. al., 2021; Banerji et. al., 2021). Corresponding figures for adenovirus vaccines such as Johnson & Johnson [J&J] Ad26.COV2.S and AstraZeneca–Oxford ChAdOx1 are around 0.0003% for blood clotting (Ledford, 2021; CDC, 2021d). Overall, as of Aug. 16, 2021, after administration of more than 357 million doses of COVID-19 vaccines, a grand total of 6,789 deaths had been reported, or 0.0019% of doses administered (CDC, 2021d), and few of these deaths have even been specifically tied to the vaccines themselves rather than extraneous factors or even coincidence. For these and many other reasons, as of Aug. 23, 2021, the Pfizer–BioNTech BNT162b2 has full rather than emergency FDA approval (USFDA, 2021).

For comparison, your odds of being struck by lightning once in an 80-year lifetime (believe it or not, the National Weather Service maintains stats on this!) are one in 15,300, or 0.0065%--more than three times the odds of a severe adverse reaction (SAR) from any COVID-19 vaccine (NWS, 2021). Apart from valid doctor-certified medical exemptions, it isn’t reasonable to refuse vaccination based on risk this low.

In conclusion, it should be also noted that there is a flood of disinformation regarding vaccine safety and effectiveness circulating on social media and in online activist and news/op-ed forums. A detailed examination of the numerous claims and allegations being made is beyond our scope today but suffice to say that virtually none of it has any basis whatsoever in fact and it continues to spread only because it receives uncritical reception in these forums outside of the scientific peer-review process.1 By the reliable data and numbers, the safety of these vaccines is also beyond reasonable dispute.

Do I still need to mask up and socially distance after vaccination?

In a word, yes… but only as the circumstances of your daily activities and regional safety guidelines dictate. Here are the things that need to be kept in mind…

As of this writing, 99% of all new COVID-19 cases in the US are the Delta variant (CDC, 2021e). As already noted, the existing Pfizer vaccine has been shown to be 79-88% effective against Delta for infection. That's tantamount to saying that it's 12-21% ineffective, meaning that even if you're vaccinated you still have roughly one chance in six of coming down with COVID-19 if exposed to it, perhaps asymptomatically.

What happens if you do...? It’s well known that breakout cases among the vaccinated can still carry viral load significant enough to be contagious even if they don't become symptomatic, and in some cases, they may even carry as much as those who aren’t vaccinated (CDC, 2021). Either way, if you do, how many susceptible people you pass it to while contagious will depend on a wide range of factors—your age and immune function, demographics of your daily encounters, behavior (including masking and social distancing), etc. Taking all these factors into account, given the average person infected with a disease, the expectation value for how many people he/she will spread it to in an unvaccinated environment while contagious is given by its base reproductive factor, or 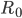R_{0}.

As of this writing, Delta has an estimated 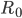R_{0} of between 5 and 9.5, as opposed to that of chickenpox, which has an 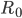R_{0} of 8.5 (CDC, 2021; UNSW, 2021; Liu & Rocklöv, 2021; Georgiou, 2021). As such, even if you are vaccinated, if you come down with a breakout case of Delta COVID-19 in an unvaccinated setting and don't quarantine or change your behavior, you will likely spread the disease to at least some people before recovering or dying. In most cases being vaccinated will reduce the likelihood that you will spread it, but it’s possible that you could spread it to as many as five to nine others. Each of them will then do likewise, and so on—more so among the unvaccinated. As successive generations of infection proceed through a given population, the number of susceptible hosts will be eroded by acquired immunity or death, and continued infection rates will to first order yield an effective reproductive factor, 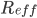R_{eff}, given by,

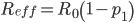
R_{eff} = R_{0}\left ( 1 - p_{1} \right )

where 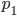p_{1} is the percentage of a population that has acquired immunity either through infection or... vaccination. As can be seen, the key to reducing 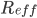R_{eff} is to increase 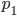p_{1}… And vaccination makes this possible at a much faster rate with orders of magnitude fewer casualties.

For Delta (or any other SARS-COV-2 variant) to be contained regionally or globally, 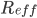R_{eff} must remain less than 1.0 long enough for the virus to die out. So, given a median 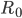R_{0} of 7.3 for the estimated range above, this means that 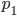p_{1} must be greater than 0.86. As of Oct. 3, 2021, total cumulative U.S. COVID-19 cases were at 43.7 million and deaths at 701,000, or around 13.1% of its population that has acquired immunity, and concurrently, 54.9% of its population is fully vaccinated (JHUM, 2021; CDC, 2021). Conservatively assuming negligible breakout case overlap, and naively presuming a normalized overall vaccine effectiveness of 88% (per the upper range of Pfizer–BioNTech Delta variant effectiveness cited above), that works out to at most, a 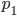p_{1} of 0.61—far short of the target needed for containment. And none of this accounts for the erosion of vaccine effectiveness by the evolution of increasingly vaccine-resistant strains, which once they break out of vaccinated hosts, spread most virulently among the unvaccinated.

What can we do? By my lights, there are three responsible options:

Option #1:  If you haven’t done so already, consider getting vaccinated.

This is by far, the best protection you can offer yourself and others against infection and/or hospitalization from all extant strains of SARS-COV-2. If you have a history of allergies and/or reactions to vaccines and are worried about whether they’re safe for you, consult your primary care doctor. You might also want to spend some time at the CDC’s COVID-19 Vaccine Information portal for more information. Bear in mind that these vaccines are free. You don't need health insurance to get them and they’re available at most pharmacies as well as clinics, including grocery store pharmacies (My wife and I got both our Pfizer shots at our neighborhood Safeway). The pharmacists there will gather the needed information regarding your risks, and consult your primary care doctor as well if need be. For safety reasons, you will be asked to remain in the waiting area for 10-30 minutes after receiving your shot. And in the extremely unlikely case that you do have a SAR (Severe Adverse Reaction) to vaccination, they will have EpiPen’s on hand that will immediately rectify all but the tiniest handful of them.

Again, this cannot be emphasized enough—There is an obscene amount of pseudoscience, conspiracy theories, and other disinformation being circulated on social media by anti-vax activists. 1 To repeat a viral mantra in these communities… Under no circumstances whatsoever should you “do your own research” on YouTube, Facebook, or any agenda-driven online forums outside of the scientific peer-review process. Your primary care doctor has your personal medical history, and properly trained pharmacists who work with COVID-19 vaccines and understand what risks they have will be able to contact him/her if there are any concerns. They and they alone can speak to whether they’re safe for you.

Option #2:  Mask and socially distance when prudent, especially indoors.

If COVID-19 vaccines aren’t a safe and viable option for you, you can still protect yourself and others by socially distancing and wearing a mask. SARS-COV-2 is spread primarily by expectorated droplets and aerosols (this is where the six-foot rule comes from) and masking dramatically decreases the spread of these droplets. Outdoors, breezes and atmospheric dispersion make this less of a concern. But indoors it’s more important, especially in smaller spaces.

The best protection is provided by medical-grade N95 masks like those manufactured by 3M’s Particulate Respirator 8211. These are the only masks that will individually block SARS-COV-2 viral transmission in both directions, protecting you as well as others. Their only downsides are limited availability, and for some people, discomfort (they tend to produce skin irritation and/or itching).

The next best thing is a high-quality 3-ply cloth mask with microfilters such as those made by Airband. Even better is double-masking—wearing a surgical mask under a 3-ply cloth one. Recent research has shown that properly done, this can reduce one’s risk of transmission and infection by 90% or more, rivaling the efficacy of mRNA vaccines (Brooks et. al., 2021). Proper use of masks is as important as mask selection, so it’s a good idea to review the CDC’s Guidelines for improving mask protection.

It also should be pointed out that agenda-driven activists on social media and in online “news” and propaganda forums are spreading even more pseudoscience and disinformation about masks and social distancing than vaccines, and virtually none of it has any basis whatsoever in fact either. 2 As before under no circumstances whatsoever should anyone be “doing their own research” in such forums outside of the scientific peer-review process.

Option #3:  Avoid crowds and prolonged indoor gatherings.

As already noted, expectorated droplets are the primary vector of transmission for SARS-COV-2. However, normal breathing does release a viral load that only a medical-grade N95 mask will stop. In outdoor or large, well-ventilated spaces this viral load is too small to make a difference. But in tightly crowded conditions and gathering in small, enclosed spaces it can build up to dangerous levels. If you don’t have access to medical-grade N95 masks, avoid crowded gatherings in poorly ventilated spaces—yes, unfortunately, that does include churches where proper circulation and social distancing measures aren’t being implemented.

Finally, bear in mind that as we have seen, even if you are vaccinated, adopting options #2 and #3 as well will still give you protection from a breakout infection, and help protect others if you do come down with one.

Whatever path we choose, let us examine our own hearts and remember that it’s not just we ourselves that we’re protecting, but our neighbors, our loved ones, and our communities. As the poet John Donne said,

“No man is an island entire of itself; every man is a piece of the continent, a part of the main; if a clod be washed away by the sea, Europe is the less, as well as if a promontory were, as well as any manner of thy friends or of thine own were; any man's death diminishes me, because I am involved in mankind. And therefore never send to know for whom the bell tolls; it tolls for thee.”

As we face our own plague—As millions of our fellow citizens suffer under the iron fist of this cruel disease, hundreds of thousands die slow, horrible, intubated deaths, and doctors and nurses put in 70/80-hour weeks at the edge of their human reserves to save lives—Luther reminds us that we are all in this together, and we’ve been called to go forth into that Valley of the Shadow of Death hand-in-hand...

Not in brashness or foolhardiness… Not in willful rejection of science and medicine… Not in service to Self and license masquerading as "freedom…"

But as living sacrifices, holy, acceptable to God, in reasonable service to each other knowing that whatever may befall us, God is by our side completing the work he began in us. "Truly I tell you, whatever you did for one of the least of these brothers and sisters of mine, you did for me" (Matt. 25:39-40).

Or in the words of Paul,

"All things are lawful, but not all things are profitable. All things are lawful, but not all things edify. Let no one seek his own good, but that of his neighbor" (I Cor. 10:23-24).

"Do nothing from selfishness or empty conceit, but with humility of mind regard one another as more important than yourselves; do not merely look out for your own personal interests, but also for the interests of others. Have this attitude in yourselves which was also in Christ Jesus, who, although He existed in the form of God, did not regard equality with God a thing to be grasped, but emptied Himself, taking the form of a bond-servant, and being made in the likeness of men. Being found in appearance as a man, He humbled Himself by becoming obedient to the point of death, even death on a cross. For this reason, also, God highly exalted Him and bestowed on Him the name which is above every name, so that at the name of Jesus every knee will bow, of those who are in heaven and on earth and under the earth, and that every tongue will confess that Jesus Christ is Lord to the glory of God the Father" (Phil. 2:3-11).

Do nothing from selfishness or conceit… Regard others as more valuable than yourself, and look to their interests as well as your own...

Have this attitude (this mindset, this worldview, these values... not these parroted dog-whistles or party-line narratives) in you which was also in Christ Jesus...

Who although He was God Incarnate, with all the power, authority, and glory thereof, did not consider that august status a thing to be grasped (clung to, defended with bared teeth and narcissistic injury), but emptied Himself, taking on the role of a servant...

And being found in mortal human form, was obedient to the point of death—even death on a cross, which in New Testament times was a death of disgrace reserved only for the lowest of despised criminals...

This is the kind of discipleship we’ve been called to… And it’s a far cry from rugged individualism and idolatrous nationalism whitewashed with joyful hymns and inspirational bumper stickers.

Say what you will about his quaint puritanical language, his belief that "evil spirits" cause plagues, and other bucolic naivetes. But like us, Luther was a man of the age he lived in. His words were penned long before he or any of his contemporaries had access to modern epidemiology, immunology, or even knowledge of germs. To dismiss him for speaking from, and to the age he lived in would be at best anachronistic, and at worst, sanctimonious. Archaic or not, in this age of COVID-19, the example he left with us is as self-evident as it is timeless, and those of us who call ourselves Christians would do well to heed it—especially those who seem to think that trusting God means tempting Him by rejecting science and medicine and behaving recklessly in the name of “freedom,” and then expecting Him to clean up their messes without holding them accountable as His sons and daughters.

We can embrace a faith like his that "makes use of intelligence and medicine" and "serves the sick for the sake of God's gracious promise." We can offer ourselves as living sacrifices, holy, acceptable to God in reasonable service to our fellow human beings and put an end to this pandemic. We can reach for the best that is in us, the best that is in our souls...

Or we can set aside loving our neighbors as ourselves (Mark 12:31) and tempt God with a "faith" based on denial, recklessness, and idolatrous worldly narratives and spread this disease throughout the world, filling hospitals and graves in our wake.

In short, we can be salt and light to a world in need... or in Luther's words, murderers.

The choice is ours. But make no mistake... We're kidding ourselves if we think we can choose the latter and expect that outside of our own echo chambers, the world isn't going to notice the difference and judge our witness accordingly.

Footnotes

1)      A deeper examination of some of the most widespread anti-vax myths currently in circulation can be found at two public Facebook posts of my own titled Covid-19 Vaccine Whack-A-Mole and Covid-19 Vaccine Whack-A-Mole - Part 2.

2)      Likewise, a deeper examination of the most widespread anti-mask myths currently in circulation can be found at a public Facebook post of my own titled Anti-Mask Whack-A-Mole.

References

Banerji, A., Wolfson, A.R., Wickner, P.G., Cogan, A.S., McMahon, A.E., Saff, R., Robinson, L.B., Phillips, E. and Blumenthal, K.G., 2021. COVID-19 Vaccination in Patients with Reported Allergic Reactions: Updated Evidence and Suggested Approach. The Journal of Allergy and Clinical Immunology in Practice. Online at https://www.jaci-inpractice.org/article/S2213-2198(21)00466-9/abstract. Accessed Oct. 3, 2021.

Baraniuk, C., 2021. Covid-19: How effective are vaccines against the delta variant? BMJ: British Medical Journal, 374. Online at https://www.bmj.com/content/374/bmj.n1960. Accessed Oct. 3, 2021.

Cavanaugh A.M., Spicer K.B., Thoroughman D., Glick C., & K. Winter. 2021. Reduced Risk of Reinfection with SARS-CoV-2 After COVID-19 Vaccination — Kentucky, May–June 2021. MMWR Morb Mortal Wkly Rep, 2021;70:1081-1083. DOI: http://dx.doi.org/10.15585/mmwr.mm7032e1. Online at https://www.cdc.gov/mmwr/volumes/70/wr/mm7032e1.htm?s_cid=mm7032e1_w. Accessed Oct. 3, 2021.

Centers for Disease Control and Prevention (CDC). 2021. Improving communications around vaccine breakthrough and vaccine effectiveness. PowerPoint presentation, July 29, 2021. Online at https://context-cdn.washingtonpost.com/notes/prod/default/documents/8a726408-07bd-46bd-a945-3af0ae2f3c37/note/57c98604-3b54-44f0-8b44-b148d8f75165. (period included in the link). Accessed Oct. 3, 2021.

Centers for Disease Control and Prevention (CDC). 2021b. COVID-19 Vaccines That Require 2 Shots. Aug. 9, 2021. Online at https://www.cdc.gov/coronavirus/2019-ncov/vaccines/second-shot.html. Accessed Oct. 3, 2021.

Centers for Disease Control and Prevention (CDC). 2021c. COVID-19 Vaccine Breakthrough Case Investigation and Reporting. Aug. 20, 2021. Online at https://www.cdc.gov/vaccines/covid-19/health-departments/breakthrough-cases.html. Accessed Oct. 3, 2021.

Centers for Disease Control and Prevention (CDC). 2021d. Selected Adverse Events Reported after COVID-19 Vaccination. Aug. 17, 2021. Online at https://www.cdc.gov/coronavirus/2019-ncov/vaccines/safety/adverse-events.html. Accessed Oct. 3, 2021.

Centers for Disease Control and Prevention (CDC). 2021e. COVID Data Tracker - Variant Proportions. Updated Sept. 22, 2021. Online at https://covid.cdc.gov/covid-data-tracker/#cases_totalcases. Accessed Oct. 3, 2021.

Callaway, E. 2021. Pfizer COVID vaccine protects against worrying coronavirus variants. Nature, May 6, 2021. Online at https://www.nature.com/articles/d41586-021-01222-5. Accessed Oct. 3, 2021.

European Medicines Agency (EMA). 2021. EMA recommends COVID-19 Vaccine AstraZeneca for authorization in the EU. Jan. 29, 2021. Online at https://www.ema.europa.eu/en/news/ema-recommends-covid-19-vaccine-astrazeneca-authorisation-eu. Accessed Oct. 3, 2021.

Evans, M. & J. Wernau. 2021. Unvaccinated Americans Are Behind Rising Covid-19 Hospitalizations. Wall Street Journal, July 18, 2021. Online at https://www.wsj.com/articles/unvaccinated-covid-19-hospitalizations-11626528110?mod=article_inline. Accessed Oct. 3, 2021.

Georgiou, A. 2021. How Contagious Are Chickenpox, Measles As CDC Document Reveals Delta Variant's R0. Newsweek, July 30, 2021. Online at https://www.newsweek.com/how-contagious-chickenpox-measles-cdc-document-delta-variant-coronavirus-r0-1614661. Accessed Oct. 3, 2021.Oct. 3

Griggs, M.B. 2014. 30,000 People In Quarantine After Bubonic Plague Kills One in China. Smithsonian, July 23, 2014. Online at https://www.smithsonianmag.com/smart-news/bubonic-plague-outbreak-china-leads-quarantine-180952136/. Accessed Oct. 3, 2021.

Haas, E.J., Angulo, F.J., McLaughlin, J.M., Anis, E., Singer, S.J., Khan, F., Brooks, N., Smaja, M. Mircus, G., Pan, K. Southern, J., Swerdlow, D.L., Jodar, L., Levy, Y., & Alroy-Preis, S. 2021. Impact and effectiveness of mRNA BNT162b2 vaccine against SARS-CoV-2 infections and COVID-19 cases, hospitalizations, and deaths following a nationwide vaccination campaign in Israel: an observational study using national surveillance data. The Lancet, May 05, 2021. Online at https://doi.org/10.1016/S0140-6736(21)00947-8. Accessed Oct. 3, 2021.

Hiltzik, M. 2021. Column: 'Death panels' arrive — in COVID-stricken Republican Idaho. Los Angeles Times, Sept. 17, 2021. Online at https://www.latimes.com/business/story/2021-09-17/death-panels-republican-covid-stricken-idaho. Accessed Oct. 3, 2021.

Johns Hopkins University & Medicine (JHUM). 2021. Coronavirus Resource Center: World Map >> US. Updated Oct. 3, 2021, 11:21 AM PT. Online at https://coronavirus.jhu.edu/map.html. Accessed Oct. 3, 2021.

Kates, J., Dawson, L., Anderson, A., Rouw, A., Michaud, J, & N. Singer. 2021. COVID-19 Vaccine Breakthrough Cases: Data from the States. Kaiser Family Foundation, July 30, 2021. Online at https://www.kff.org/policy-watch/covid-19-vaccine-breakthrough-cases-data-from-the-states/. Accessed Oct. 3, 2021.

Knowles, H. 2021. Hospitals overwhelmed by covid are turning to 'crisis standards of care.' What does that mean? Washington Post, Sept. 22, 2021. Online at https://www.washingtonpost.com/health/2021/09/22/crisis-standards-of-care/. Accessed Oct. 3, 2021.

Ledford, H., 2021. COVID vaccines and blood clots: five key questions. Nature, 592(7855), pp.495-496. Online at https://www.icpcovid.com/sites/default/files/2021-04/Ep%20132-12%20COVID%20vaccines%20and%20blood%20clots_%20five%20key%20questions.pdf. Accessed Oct. 3, 2021.

Liu, Y. and Rocklöv, J., 2021. The reproductive number of the Delta variant of SARS-CoV-2 is far higher compared to the ancestral SARS-CoV-2 virus. Journal of Travel Medicine. Online at https://academic.oup.com/jtm/advance-article/doi/10.1093/jtm/taab124/6346388. Accessed Oct. 3, 2021.

Lopez Bernal, J., Andrews, N., Gower, C., Gallagher, E., Simmons, R., Thelwall, S., Stowe, J., Tessier, E., Groves, N., Dabrera, G. and Myers, R., 2021. Effectiveness of Covid-19 vaccines against the B. 1.617. 2 (delta) variant. New England Journal of Medicine. Online at https://www.nejm.org/doi/full/10.1056/NEJMoa2108891. Accessed Oct. 3, 2021.

Luther, M. 2020. Whether One May Flee From A Deadly Plague. Aug. 1527. Reprinted in Christianity Today, May 19, 2020. Online at https://www.christianitytoday.com/ct/2020/may-web-only/martin-luther-plague-pandemic-coronavirus-covid-flee-letter.html. Accessed Oct. 3, 2021.

Mahase, E. 2020. Covid-19: Moderna vaccine is nearly 95% effective, trial involving high risk and elderly people shows. BMJ: British Medical Journal (Online), 371. Online at https://search.proquest.com/openview/f23612d9e0218b4d0ee67dcdb5c57884/1?pq-origsite=gscholar&cbl=2043523. Accessed Oct. 3, 2021.

Mallapaty, S. and Callaway, E., 2021. What scientists do and don't know about the Oxford-AstraZeneca COVID vaccine. Nature, 592(7852), pp.15-17. Online at https://www.icpcovid.com/sites/default/files/2021-03/Ep%20123-2%20What%20scientists%20do%20and%20don%E2%80%99t%20know%20about%20the%20Oxford%E2%80%93AstraZeneca%20COVID%20vaccine.pdf. Accessed Oct. 3, 2021.

National Weather Service (NWS). 2021. How Dangerous is Lightning? Online at https://www.weather.gov/safety/lightning-odds. Accessed Oct. 3, 2021.

Noor, R. 2021. Developmental Status of the Potential Vaccines for the Mitigation of the COVID-19 Pandemic and a Focus on the Effectiveness of the Pfizer-BioNTech and Moderna mRNA Vaccines. Current clinical microbiology reports, Mar. 3, 2021, pp.1-8. Online at https://link.springer.com/article/10.1007/s40588-021-00162-y. Accessed Oct. 3, 2021.

Oliver, S.E. et. al. 2020. The Advisory Committee on Immunization Practices' Interim Recommendation for Use of Moderna COVID-19 Vaccine—United States, December 2020. MMWR. Morbidity and mortality weekly report, 69. Online at https://www.cdc.gov/mmwr/volumes/69/wr/mm695152e1.htm. Accessed Oct. 3, 2021.

Olliaro, P., Torreele, E. and Vaillant, M. 2021. COVID-19 vaccine efficacy and effectiveness—the elephant (not) in the room. The Lancet Microbe. Online at https://www.thelancet.com/journals/lanmic/article/PIIS2666-5247(21)00069-0/fulltext?s=08. Accessed Oct. 3, 2021.

Polack, F.P., Thomas, S.J., Kitchin, N., Absalon, J., Gurtman, A., Lockhart, S., Perez, J.L., Pérez Marc, G., Moreira, E.D., Zerbini, C. and Bailey, R. 2020. Safety and efficacy of the BNT162b2 mRNA Covid-19 vaccine. New England Journal of Medicine, 383(27), pp.2603-2615. Online at https://www.nejm.org/doi/full/10.1056/NEJMoa2034577. Accessed Oct. 3, 2021.

Ritchie, H., Ortiz-Ospina, E., Beltekian, D., Mathieu, E., Hasell, J., Macdonald, B., Giattino, C., Appel, C., Rodés-Guirao, L., and M. Roser. 2021. Coronavirus (COVID-19) Vaccinations. Our World In Data, May 6, 2021. Online at https://ourworldindata.org/covid-vaccinations. Accessed Oct. 3, 2021.

Rosenberg ES, Holtgrave DR, Dorabawila V, et al. New COVID-19 Cases and Hospitalizations Among Adults, by Vaccination Status — New York, May 3–July 25, 2021. MMWR Morb Mortal Wkly Rep 2021;70:1306–1311. Online at http://dx.doi.org/10.15585/mmwr.mm7037a7. Accessed Oct. 3, 2021.

Rutkowski, K., Mirakian, R., Till, S., Rutkowski, R. and Wagner, A. 2021. Adverse reactions to COVID‐19 vaccines: a practical approach. Clinical & Experimental Allergy. Online at https://onlinelibrary.wiley.com/doi/full/10.1111/cea.13880. Accessed Oct. 3, 2021.

Schiferl, E., 1983. Iconography of Plague Saints in Fifteenth-century Italian Painting. Fifteenth Century Studies, 6, p.205. Online at https://www.proquest.com/openview/b63edc66b065c7024f2bf4ba28c1a661/1?pq-origsite=gscholar&cbl=1818258. Accessed Oct. 3, 2021.

Scobie HM, Johnson AG, Suthar AB, et al. Monitoring Incidence of COVID-19 Cases, Hospitalizations, and Deaths, by Vaccination Status — 13 U.S. Jurisdictions, April 4–July 17, 2021. MMWR Morb Mortal Wkly Rep 2021;70:1284–1290. Sept. 17, 2021. Online at https://www.cdc.gov/mmwr/volumes/70/wr/mm7037e1.htm?s_cid=mm7037e1_w. Accessed Oct. 3, 2021.

Self WH, Tenforde MW, Rhoads JP, et al. Comparative Effectiveness of Moderna, Pfizer-BioNTech, and Janssen (Johnson & Johnson) Vaccines in Preventing COVID-19 Hospitalizations Among Adults Without Immunocompromising Conditions — United States, March–August 2021. MMWR Morb Mortal Wkly Rep. ePub: 17 September 2021. Online at http://dx.doi.org/10.15585/mmwr.mm7038e1. Accessed Oct. 3, 2021.

Shimabukuro, T.T., Cole, M. and Su, J.R., 2021. Reports of anaphylaxis after receipt of mRNA COVID-19 vaccines in the US—December 14, 2020-January 18, 2021. Jama, 325(11), pp.1101-1102. Online at https://jamanetwork.com/journals/jama/article-abstract/2776557. Accessed Oct. 3, 2021.

Smout, A. 2021. English study finds 50-60% reduced risk of COVID for double-vaccinated. Reuters, Aug. 3, 2021. Online at https://www.reuters.com/world/uk/english-study-finds-50-60-reduced-risk-covid-double-vaccinated-2021-08-03/. Accessed Oct. 3, 2021.

Stamatatos, L., Czartoski, J., Wan, Y.H., Homad, L.J., Rubin, V., Glantz, H., Neradilek, M., Seydoux, E., Jennewein, M.F., MacCamy, A.J. and Feng, J., 2021. mRNA vaccination boosts cross-variant neutralizing antibodies elicited by SARS-CoV-2 infection. Science, Vol. 372, No. 6549. Online at https://science.sciencemag.org/content/372/6549/1413. Accessed Oct. 3, 2021.

Tanne, J.H., 2020. Covid-19: FDA panel votes to approve Pfizer BioNTech vaccine. BMJ 2020;371:m4799. Online at https://www.bmj.com/content/371/bmj.m4799. Accessed Oct. 3, 2021.

Tenforde, M.W. et. al. 2021. Effectiveness of Pfizer-BioNTech and Moderna Vaccines Against COVID-19 Among Hospitalized Adults Aged≥ 65 Years—United States, January–March 2021. MMWR. Morbidity and Mortality Weekly Report, 70. Online at https://www.cdc.gov/mmwr/volumes/70/wr/mm7018e1.htm. Accessed Oct. 3, 2021.

Tregoning, J.S., Flight, K.E., Higham, S.L. et al. Progress of the COVID-19 vaccine effort: viruses, vaccines and variants versus efficacy, effectiveness and escape. Nat Rev Immunol (2021). https://doi.org/10.1038/s41577-021-00592-1. Online at https://www.nature.com/articles/s41577-021-00592-1. Accessed Oct. 3, 2021.

University of New South Wales (UNSW). 2021. What We Now Know About the SARS-CoV-2 Delta Variant That's Wreaking Havoc Globally. Press release, Aug. 4, 2021. Online at https://scitechdaily.com/what-we-now-know-about-the-sars-cov-2-delta-variant-thats-wreaking-havoc-globally/. Accessed Oct. 3, 2021.

U.S. Food and Drug Administration (USFDA). 2020. Comirnaty and Pfizer-BioNTech COVID-19 Vaccine. Coronavirus Disease 2019 (COVID-19) press release, Aug. 23, 2021. Online at https://www.fda.gov/coronavirus-disease-2019-covid-19/comirnaty-and-pfizer-biontech-covid-19-vaccine. Accessed Oct. 3, 2021.

Westneat, D. 2021. 'Sophie’s choice, over and over': Death panels are the new phase of the pandemic. Seattle Times, Sept. 11, 2021. Online at https://www.seattletimes.com/seattle-news/health/sophies-choice-over-and-over-death-panels-are-the-new-phase-of-the-pandemic/. Accessed Oct. 3, 2021.

White, A. 2014. Plague and Pleasure: The Renaissance World of Pius II. CUA Press. ISBN: 0813226813, 9780813226811. Online at https://books.google.com/books?id=SfIdBgAAQBAJ. Accessed Oct. 3, 2021.

Posted in History, Theology, Uncategorized | 8 Comments

Creator, Redeemer, and Sanctifier

by Aron Wall Posted on May 30, 2021

Our Father, the Creator

In the beginning God created the heavens and the earth.  (Genesis 1:1)

For us there is but one God, the Father, from whom all things came and for whom we live... (1 Cor 8:6)

Jesus Christ, the Creator

In the beginning was the Word, and the Word was with God, and the Word was God.  He was with God in the beginning.  Through him all things were made; without him nothing was made that has been made.  In him was life, and that life was the light of all mankind.  (John 1:1-3)

...and there is but one Lord, Jesus Christ, through whom all things came and through whom we live.  (1 Cor 8:6)

Holy Spirit, the Creator

Now the earth was formless and empty, darkness was over the surface of the deep, and the Spirit of God was hovering over the waters.  And God said, “Let there be light,” and there was light...  (Genesis 1:2-3)

When you send forth your Spirit, they are created;
And you renew the face of the earth.  (Psalm 104:30)

                                                                                                                                                                     

Our Father, the Redeemer

But it was because the LORD loved you and kept the oath he swore to your ancestors that he brought you out with a mighty hand and redeemed you from the land of slavery, from the power of Pharaoh king of Egypt.  (Deuteronomy 7:8)

But you are our Father, though Abraham does not know us or Israel acknowledge us; you, LORD, are our Father, our Redeemer from of old is your name.  (Isaiah 63:16)

Jesus Christ, the Redeemer

For you know that it was not with perishable things such as silver or gold that you were redeemed from the empty way of life handed down to you from your ancestors, but with the precious blood of Christ, a lamb without blemish or defect.
(1 Peter 1:18-19)

Christ has redeemed us from the curse of the law, having become a curse for us (for it is written, “Cursed is everyone who hangs on a tree”).
(Gal 3:13)

Holy Spirit, the Redeemer

And not only the creation, but we ourselves, who have the firstfruits of the Spirit, groan inwardly as we wait eagerly for adoption as sons, the redemption of our bodies.  (Rom 8:23)

And grieve not the Holy Spirit of God, whereby ye are sealed unto the day of redemption.  (Ephesians 4:30)

                                                                                                                                                                     

Our Father, the Sanctifier

Now may the God of peace Himself sanctify you completely...
(1 Thess 5:23)

"Holy Father, protect them by the power of your name, the name you gave me, so that they may be one as we are one.... Sanctify them by the truth; your word is truth."
(John 17:11,17)

Jesus Christ, the Sanctifier

Husbands, love your wives, even as Christ also loved the church, and gave himself for it; that he might sanctify and cleanse it with the washing of water by the word, that he might present it to himself a glorious church, not having spot, or wrinkle, or any such thing; but that it should be holy and without blemish.
(Ephesians 5:25-27)

for both he who is sanctifying and those sanctified are all of one [family], for which cause he [i.e. Jesus, the only person of the Trinity who became a human] is not ashamed to call them brethren (Hebrews 2:11)

Holy Spirit, the Sanctifier

He gave me the priestly duty of proclaiming the gospel of God, so that the Gentiles might become an offering acceptable to God, sanctified by the Holy Spirit. (Rom 15:16)

But you were washed, you were sanctified, you were justified in the name of the Lord Jesus Christ and by the Spirit of our God.  (1 Cor 6:11)

Posted in Theology | 6 Comments

Comparing Religions IX: Delayed Return

by Aron Wall Posted on May 23, 2021

This is a special bonus post in my Comparing Religions series...  I originally wrote it as a section of the post about evidence of fraud, but it seemed to work better thematically as its own post.

Unfulfilled Prophecies

Another point worth considering is the question of false prophecies, that fail to come true on schedule.  As the Book of Deuteronomy indicates, these are one possible sign of a false prophet:

You may say to yourselves, “How can we know when a message has not been spoken by the Lord?”

If what a prophet proclaims in the name of the Lord does not take place or come true, that is a message the Lord has not spoken. That prophet has spoken presumptuously, so do not be alarmed.  (18:21-22)

As an example, the Watchtower Society is particularly notorious for a history of making false predictions and then creatively reinterpreting them.  For example they claimed Jesus would return to Earth in 1914, and then when that failed to occur decided that that date was when he started reigning "invisibly", a serious anticlimax.

It would be tedious, and require an entire dissertation, to enumerate all of the examples of failed prophecy among various cults.  (To be truly complete I ought to try to examine at least the major religions, but this post will be mainly Christianity-centered.)

(Incidentially, "prophecy" is a much broader concept than predicting the future—a prophet is anyone with a message from God (or one of the gods, in polytheistic religions); and such messages can concern the past or present just as often as predicting the future.  The questions "What is God like?" and "How should people behave?" are central to how prophecy is conceived in Abrahamic religions.  So the colloquial definition of prophecy,as "predicting the future" is far too narrow to describe prophecy as classically conceived.  Neverthless, prophecy in the Bible certainly does also contain numerous predictions about the future, and that is the concern of this post.)

Prophecy and Evidence

Obviously, if a prophecy comes true in a verifiable manner, that counts as (some) evidence for the religion in question.  (How much evidence, depends on a variety of factors, including (1) how certain it is that the prophecy was written down before the events it predicted, (2) how unlikely the event was to occur naturally, and (3) the degree to which the new prophecy is consistent with previous revelations, etc.)

Conversely, if a prophecy has not come to pass, this could count as evidence against the religion.  It is however important to make a distinction between an unfulfilled prophecy, and a falsified prophecy.

An unfulfilled prophecy is one that simply has not happened yet.  For example, the claim of all Abrahamic religions that God will raise every human being from the dead at the Final Judgement has not been fulfilled yet.  However, the fact that this has not happened yet does not mean it is not going to!  After all, events in the future are not (apart from the prophecy itself) observable in the present.  (Of course, the universal resurrection of the dead is quite impossible in a Naturalistic worldview, but here we are discussing religious worldviewsin which God exists, and has the power to do miracles.)

Thus, an unfulfilled prophecy does not necessarily provide much evidence or or against a religion, unless there is good reason to think it should already have happened, or that it is impossible for it to occur.

(In Bayesian terms, if a prophecy being fulfilled counts as evidence for a religion, a prophecy not being fulfilled always counts as some evidence against the religion, so long as there is a nonzero chance that the prophecy could have already been fulfilled by now.  But under favorable circumstances, for example when the prophecy is plausibly about the distant future, the amount of disconfirmation can be quite small.)

On the other hand, a falsified prophecy is one that is definitely not going to occur.  (At least, absent some major reinterpretation of what it means.  Such reinterpretation is often a logically possibility, but one that must be paid for evidentially if the new interpretation is implausible.  One should be especially suspicious when the prophet himself engages in creative reinterpretation, since there are obvious self-justifying motivations there.  Especially if the prophet tried to convince people to take it literally before the events were falsified, and only spins the prophecy after people start complaining it didn't happen.)

The most common reason for a prophecy to be falsified is if the prophet placed some date or time constraint on the prophecy.  If the date comes to pass, and the event didn't occur, and if there is no valid excuse for God to pull a fast one and change his plan, then whoops it looks like you've been following a false prophet!  Time to repent and find a better religious guide.  On the other hand, a merely unfulfilled prophecy is perfectly compatible with the truth of a religion.

Swords to Plowshares

All of this makes it sound like prophecy exists solely for purposes of apologetic arguments.  From this perspective, a not-yet fulfilled prophecy is a wash, and may seem irrelevant.

This is a misconception.  Just because a prophecy is unfulfilled, doesn't mean it isn't important to the present.  In fact, if it weren't spiritually relevant in some way to the time period before the fulfillment, there would be no point in God revealing it.  For example, when Isaiah says that:

[The Lord] will judge between the nations
and will settle disputes for many peoples.
They will beat their swords into plowshares
and their spears into pruning hooks.
Nation will not take up sword against nation,
nor will they train for war anymore.  (2:4)

it is immediately obvious that this prophecy (universal peace) has not yet come true.  But that is not the only thing going on in the mind of a reader.  We are also struck by the thought that it ought to be true.  The goal is accepted as valid by the heart, even before the mind rejects it as a fact.

Ending war is precisely the sort of thing that a benevolent God should do.  And if he has not done it yet, it still tells us something about God that he has promised to do it.  And it tells us something about the human race, that we instinctively accept it as an ideal, even as we fall so far short of the reality.  This is why the prophet goes on to say:

"Come, descendants of Jacob, let us walk in the light of the LORD."  (2:5)

In other words, the belief in future universal peace can inspire us to be peacemakers in a more limited way today.  Even though it will take an act of God to make the reality of peace universal, taking it as the ideal still influences how we see the world of today.  (Indeed, it is probably not be an exaggeration to say that the modern international ideal of working towards "world peace" would probably not exist if the Hebrew prophets had never spoken.  This ethical imperative still inspires us as moderns, even if many have forgotten its source.)

The Second Coming

With this in mind, let us consider Jesus' own claims about his Second Coming, since this is one of the few skeptical objections specific to Christianity which is worth taking seriously.

The ministry of Jesus intersects prophecy along multiple axes.  For example, there is a conversation to be had about the many ways in which Jesus' ministry fulfilled the prophecies in the Hebrew Bible.  This was the topic of some previous posts.

But Jesus also made some predictions about the future, and the most important one has to do with his return to Earth to judge the world (and to usher in the universal peace between nations we've just been discussing!)  This is called the Second Coming.

For those less familiar with Christian theology: it is important that this Second Coming does not refer to some new incarnation as another human person born subsequent to Jesus Christ.  It refers to Jesus himself returning to Earth with the same human flesh that was born of a Jewish girl, nailed to a cross, and which is now immortal and glorified—but still fully human!—in the immediate presence of God.  (Whatever that means... Christians do not believe that God the Father literally has a body, so the sense of "presence" here is some mode other than spatial location.  In the Lord's Prayer, "Heaven" is identified as the place where God's will is perfectly done.)

As it says in Psalm 110, in a verse quoted by the New Testament many times:

The LORD says to my lord:
“Sit at my right hand
until I make your enemies
a footstool for your feet.” (Psalm 110:1)

In Christian interpretation, this passage means: God says to the Messiah, ascend to where I am and rule from there, until some future time when I will make all of your enemies submit to you.  This logically implies, that there will be a period of time after Christ ascends to Heaven, but before everyone recognizes him as their Lord.

Jesus on the Timing

Now obviously, if Jesus really talked about his coming back after an absence, this indicates that he saw at least some chronological gap between his present ministry and that future date.  The Gospels also portray Jesus as foreseeing his own humiliation and death.  This indicates that he had a far better grasp on reality than the typical first-century Messianic claimant, who expected to overthrow the Romans and set up an earthly kingdom in Judea, along the lines of the Maccabean revolt which took place a couple centuries before.

But it is sometimes claimed (especially by certain biblical scholars) that Jesus made a point of predicting that his return would be soon, within a single generation; and that when this failed to occur the Church retrospectively changed their understanding.  This is a serious accusation, and if true would significantly affect the New Testament's credibility.  It is true that there are a few passages in the Gospels which can be interpreted as making such predictions.  But this interpretation is not simple, seeing as there are also a great many passages indicating the opposite.

In fact, in most of his parables about the subject, Jesus usually implies that the Bridegroom's or Master's return will take a long time, and that many people will get tired of waiting.  Again and again, he makes a point of saying that the timing will be a surprise:

“Therefore keep watch, because you do not know on what day your Lord will come.  But understand this: If the owner of the house had known at what time of night the thief was coming, he would have kept watch and would not have let his house be broken into.  So you also must be ready, because the Son of Man will come at an hour when you do not expect him.”  (Matt 24:42)

and that not even he could predict the date:

“But about that day or hour no one knows, not even the angels in heaven, nor the Son, but only the Father.”  (Mark 13:32)

A More Problematic Passage

But what about the passage in which Jesus says:

“Truly I tell you, this generation will certainly not pass away until all these things have happened.” (Matt 24:34) ?

In his essay “The World’s Last Night”, C.S. Lewis interpreted this as a rare example of Jesus being in error, writing that:

It is certainly the most embarrassing verse in the Bible.

but he suggests it is nevertheless compatible with Christian theology because:

The one exhibition of error and the one confession of ignorance [i.e. Mark 13:32] grow side by side.

However I do not accept St. Lewis' interpretation as a valid solution to this problem.  Yes, Jesus did confess ignorance (at least with respect to his human knowledge), but the appropriate response to ignorance is to remain silent, not to make a bold and possibly erroneous prediction!

It is true that in orthodox Chalcedonian theology, Christ is regarded as being fully human as well as fully divine.  His human nature was just like ours in every way but sin.  And ignorance is not the same thing as sin.  Thus, even though Christ was God and therefore knew everything with respect to his divine omniscience, it does not follow that he knew every fact according to human modes of knowledge.  (Presumably an infinite number of facts can't fit into an ordinary human brain, at least in this life, even if that human brain is fully united with the divine Logos.)  Anyway, St. Luke tells us quite explicitly that Jesus "grew in wisdom and stature" (Luke 2:52) as a child, and growth in wisdom implies learning.

However, none of this leads me to think that Christ could have made a major blunder of theology with respect to his public teaching.  After all, Christ's words were guided by the Holy Spirit, even more so than in the case of an ordinary prophet, seeing as he was filled with the Spirit "without measure" (John 3:34).  Christ's teachings in the New Testament have spiritual authority; and thus it would be a major, major problem for Christianity if Jesus had given an untrue prophecy, especially about such a central point.

My Preferred Explanation

I would rather explain this passage with reference to its full context.   All of the verses just quoted are contained within a discourse called the Olivet Discourse, which begins with a question asked by the disciples on the Tuesday before the Crucifixion.  There are three different versions of this speech in different gospels.  Notably, in St. Matthew's version, the disciples' question has two parts (numbers and brackets mine):

Jesus left the temple and was walking away when his disciples came up to him to call his attention to its buildings.  “Do you see all these things?” he asked. “Truly I tell you, not one stone here will be left on another; every one will be thrown down.”

As Jesus was sitting on the Mount of Olives, the disciples came to him privately. “Tell us,” they said,

(1) “when will this happen, [i.e. the Destruction of the Temple]

(2)  and what will be the sign of your coming and of the end of the age?”

It can be seen that these are two separate questions, and that (whatever the disciples might have thought when they asked them) the correct chronological answers two these two questions are also quite different.

Regarding (1), the Temple in Jerusalem was destroyed in AD 70 by the Romans, which is indeed within one generation (the Jews conventionally reckoned a generation as being 40 years long, and Jesus died around 30-33 AD).  So this part of the prophecy is actually a spectacular success.

(Many of Jesus' subsequent predictions also seem to have come true: that Christians would go on to be persecuted, that the Gospel would be preached to all nations, that many false prophets would arise, and that "wars and rumors of wars" would go on during all this time, as they always do.  However, the emphasis of this part of the speech is more about Jesus forewarning the disciples about the problems they will face, rather than gratifying the disciples' curiosity about the exact shape of future history.)

Regarding (2), Jesus has not yet returned, so there's been a delay of at least 1988 years, as of the time of this blog post.

And we can give up any idea of an "invisible" coming, or coming in an obscured way as some other historical person, seeing as Jesus is pretty explicit that his Second Coming will be totally obvious to everyone when it finally happens:

“At that time if anyone says to you, ‘Look, here is the Messiah!’ or, ‘There he is!’ do not believe it.  For false messiahs and false prophets will appear and perform great signs and wonders to deceive, if possible, even the elect.  See, I have told you ahead of time.

So if anyone tells you, ‘There he is, out in the wilderness,’ do not go out; or, ‘Here he is, in the inner rooms,’ do not believe it.  For as lightning that comes from the east is visible even in the west, so will be the coming of the Son of Man.”

So to fully answer the disciples' question, Jesus needs to provide two different chronological answers, and in fact Jesus gives both correct answers—the answer to (1) is "this generation shall certainly not pass away", while the answer to (2) is that nobody has any clue when it will happen, not even the Son himself!  Without this assumption, it is difficult to read the text as even consistent with itself, let alone history.

Indeed, the account in Luke's Gospel does seem to anticipate a chronological gap between (1) and (2), with a pivot at the verse which says:

Jerusalem will be trampled on by the Gentiles until the times of the Gentiles are fulfilled.

which seems to suggest an unknown interval of time, and separates the predictions related to the Destruction of the Temple from the predictions related to the End Times (although not from the sayings about timing).

It is true that the chronological answers to  (1) and (2) are not clearly organized in the Gospels as we have them.  The Synoptic Gospels were most likely written before the Destruction of the Temple (arguments to the contrary tend to be based on the Methodologically Naturalist assumption that predictive prophecy is impossible).

Jesus himself may have been grouping the two events thematically, as two examples of Tribulation/Judgement.  Not unlike how the prophet Isaiah likes to talks about the Resurrection and the Return from Exile in conjunction with each other.  Both are showing history more from God's perspective, rather than from a human perspective.  (We already knew what the human perspective looks like!)

It seems probable that the disciples themselves were confused by this, and did not clearly distinguish Jesus' words about timing with respect to their proper referents.  The fact that the Church preserved four different accounts of Jesus' life, in which the wordings of the same speech is often slightly different, acknowledges the reality that Jesus is a historical figure and that our knowledge of his life is mediated through human witnesses.

(This does not, I think, contradict any Christian doctrines about divine inspiration of the Gospels.  The Christian version of inspiration is that the Holy Spirit guided the writing process so as to reveal the truths he wanted to reveal; and that every single part of the Bible is, in this sense, the word of God; and thus authoritative and Christ-revealing.  It does not mean that all the truths in Scripture are always exposited in an equally clear and manifest fashion, without obscurity.  Nor does it mean that the documents are in no way limited by the human perspectives of their authors, or somehow not subject to the vicissitudes of the textual copying process.  The Bible is divine words and human words at the same time, and neither authorship negates the other.  This means that the Bible is not always the book that Fundamentalists want it to be.  But I very much doubt that having that book would have been good for us!)

Another Verse

As for the similar sounding verse in Mark 9:1:

And he said to them, "Truly I tell you, some who are standing here will not taste death before they see that the kingdom of God has come with power."

I would interpret this verse as referring, not to the Second Coming (nor to the Transfiguration which immediately follows, as the guy who divided up the Bible into chapters apparently thought) but rather to Jesus' Resurrection and the inauguration of the Church, which was indeed the establishment of God's kingdom in Christian theology.

Jesus overcoming human sin and death, appearing to chosen witnesses, and sending the Holy Spirit to soften human hearts, does not seem like quite as much of an inconsequential anti-climax as a hypothetical coming in 1914 that didn't seem to change anything for anyone.  But then I would say that as a Christian, wouldn't I?

Weighing Evidence

Since this is a series about comparing evidence for different religions, the question must be raised: to what extent should these sorts of rationalizations count as plausible explanations to skeptics, or for those in non-Christian traditions?

Here, I think it is important to get over the idea that a problem in biblical theology must either be a killing blow which refutes a religion entirely; or else it is no big deal and can be safely ignored after one accepts a pat explanation.  It is possible for an apparent theological discrepancy to provide some mild evidence against a religion, if there are plausible-sounding explanations, but those explanations also seem a bit contrived in other respects.  To determine how significant the problem is, one would then need to consider the rest of the cumulative case for the religion.

So it is perfectly possible for me to admit that some verses of the Bible provide some evidence against Christian doctrines, without immediately throwing the whole system overboard.  Instead one has to accept some things on the credit of the system as a whole.  I hope I am showing the same courtesy to the non-Christian religions, by not over-emphasizing isolated difficulties, but instead trying to assess what seem to be the key issues.

It would be quite astonishing if there were no difficulties to get over in the interpretation of any text which is thousands of years old, and which purports to reveal the intrusion of something from outside the spacetime continuum.  If there were no difficulties, that would itself be a difficulty, since it would be the mark of a human-made religion with no sharp corners or untidy edges.  (Quantum mechanics is weird, why shouldn't theology be too?)

Descent of the Spirit

OK, somebody might say, but even if you can get over the fact of Jesus' own predictions, it's still true that he didn't fulfill all of the Messianic prophecies, or any of them in the particular way that the Jews were expecting.  The Jews expected the Messiah to set up an earthly kingdom.  Jesus didn't.  Even if you can get over the comments about "this generation", isn't this still an ad hoc attempt to get over the embarrassing problem that Jesus never fulfilled half the stuff he was supposed to do?  The swords were never all beaten into plowshares, and it doesn't look like our nuclear missiles are going to be reforged into tractors anytime soon either!

I agree that this delay may seem strange to a person who is not themselves caught up into the story of Jesus.   But I do not think it is so arbitrary as it might seem at first.  Even in the period between Jesus' Resurrection and his Ascension to Heaven, it was still hard for the disciples to give up the idea of an immediate earthly kingdom:

After his suffering, he presented himself to them and gave many convincing proofs that he was alive. He appeared to them over a period of forty days and spoke about the kingdom of God.

On one occasion, while he was eating with them, he gave them this command: “Do not leave Jerusalem, but wait for the gift my Father promised, which you have heard me speak about.  For John baptized with water, but in a few days you will be baptized with the Holy Spirit.”

Then they gathered around him and asked him, “Lord, are you at this time going to restore the kingdom to Israel?”  (Acts 1:3-6)

Jesus reminds them, quite conspicuously, that the time of the Second Coming is unknown, and re-directs their attention to a different promise:

He said to them: “It is not for you to know the times or dates the Father has set by his own authority.  But you will receive power when the Holy Spirit comes on you; and you will be my witnesses in Jerusalem, and in all Judea and Samaria, and to the ends of the earth.”  (1:7-8, emphasis mine)

Given these words, it seems pretty hard to imagine that St. Luke (the author of Acts) was under the impression that Jesus had committed himself to a definite timetable for the Second Coming.

The central story of Christianity is that of a rejected, suffering, forgiving Messiah.  What is the natural conclusion of the story?  A ruling, peacemaking Messiah, yes; but first something else.  I am afraid that from God's point of view, the next installment of the story involves us.  Christ says to his disciples: "I bled and died for you out of love.  Now you must do the same thing.  And if you are willing to do it, I will give you my Spirit to guide you."  [Not a direct quote, but clear enough from the Gospels.]

I can see why one would not want to hear these words, but from an aesthetic and theological point of view, they make perfect sense.  If we humans are in the image of God, then wherever God leads, we must follow.  As he sacrificed his live for us, we must now sacrifice our lives for one another, even for those who do not yet believe.  We too must live out the Christian life, even if it means we will be rejected and despised (in which case we must also forgive!).

We are called to be saints; the holy ones of God.  How can we think we will be excused from suffering?  If Christ had come in a single generation, then where would St. Francis and St. Corrie Ten Boom and Mother Theresa be?  Where would the martyrs be?  Nowhere; they would not exist.

Nor should we excuse ourselves from the call to holiness.  Even if our own spiritual fruits are not yet so great as these, there is no telling what God may do with us in the future, if we allow him.

Many generations of Christians have been tempted to think that things have gotten bad enough that Christ should return and put an end to human misery.  Yet, looking back on history we can see that the human growth and development of the Church would have been incomplete, without all the chances to build monasteries, universities, reformations, modern science, civil rights movements, etc.  All of these historical situations—with their unique mixes of good and bad—have been settings where the saints have needed to creatively adapt the life of Christ, to new situations.  (In another thousand years, perhaps we will be thinking how much we would have lost if history had ended before space travel!)

We human beings may often fail the tests that history presents, but I do not think this matters quite as much as one might think.  Even failure allows for learning, just as suffering allows for growth.  To be sure, the whole story would come to nothing, if Christ were not coming to deliver us in the end.  But if he does bring the whole thing to a satisfactory conclusion, I think we can see why that conclusion might be better if it comes later, rather than sooner.

Pentecost 2021

Next: Moral Depth

Posted in History, Theological Method | 7 Comments

Friendship with Non-Christians

by Aron Wall Posted on May 8, 2021

I received this email from someone I know:

Hey Aron,

It's been quite a while. How are things going? Enjoying your time across the pond?

I'm curious about your thoughts on having close non-Christian friends. I've known my best friend, who is non-Christian, since college. I was the best man in his wedding. His kids call me 'uncle'. So I clearly see nothing wrong with it. I've come across a number of articles, though, that argue that believers should not have unbelievers as close friends, and that the primary purpose of having a casual friendship with them should be to try and convert them. Take, for example, the following:

"We are called to evangelize the lost, not be intimate with them. There is nothing wrong with building quality friendships with unbelievers – but the primary focus of such a relationship should be to win them to Christ by sharing the Gospel with them and demonstrating God’s saving power in our own lives." (https://www.gotquestions.org/friendships-unbelievers.html)

This seems to be a pretty consistent theme across various articles on the topic. I always like hearing your view on various things so I'm curious to hear what you think.

I replied approximately as follows:

Good to hear from you.  I consider the idea you mention to be a heresy straight from the blackest, stinkiest pit of Hell.

1.  The commandment is to "Love your neighbor as yourself", not "Love your neighbor, but only if they are a fellow Christian."  But love naturally leads to friendship, whenever there are shared interests and interactions making it possible.

The author of this article apparently allows for "quality" friendships, but not for "intimate" or "deep" ones—but I'm not sure this distinction makes very much logical sense.  Leaving romance aside, what could be more intimate than talking about the most important things in one's own spiritual life?

2.  The advice to avoid becoming close doesn't make any sense practically either.  Becoming close friends with somebody is THE most effective form of evangelism (certainly in my own experience), but only if it is done sincerely and in good faith.

You can't know in advance when or if a friendship will lead to an opportunity to explicitly share the Gospel in a way that the other person will be receptive to.  Sometimes it takes 5 years, 10 years, even 50 years to get to that point.  So when are you supposed to show that person the door and eject them as a lost cause?

Imagine saying to a non-Christian: "I'm going to act friendly with you, but all I'm really interested in is converting you.  If you don't show any signs of listening to my gospel shpiels within a few months or so, then I'll put up barriers to make sure this doesn't develop into a close friendship.  Please don't share your deepest heart-concerns with me, unless you make it obvious that it's a possible prelude to conversion.  And I in turn will make sure to never share my deepest struggles with you."

What a horrible thing that would be to say out loud!  It makes me feel sick just to write it.  Wouldn't any non-Christian quite reasonably be offended by that?  Wouldn't it confirm all their worst suspicions about us, as judgmental sanctimonious hypocrites?  That all we care about is using them to score religious points?

But you might ask, isn't trying to lead people to Christ and thus saving their souls the highest form of love?  Isn't that far more important, and thus loving, than say hanging out and talking about movies or football?

Yes and no.  The REALITY of our neighbor's soul is of course infinitely more valuable than any of their worldly interests.  That is why the person who gives up their eye, hand, or even life for salvation will find that their true self is the one that is in Jesus.

But, our own CONCEPT of what is going on in our neighbor's soul is in many ways imaginary, and is therefore often much less real than their secular interests. That's why we are commanded to get involved with our neighbors' lives in concrete ways---like sharing meals with them or visiting them when they are sick.  It is the concrete person, the same one who loves BBQ and funny Youtube videos, whom Christ came to save.  The visible self of our neighbor, is usually the most real self we have access to, and therefore the self we are to love as ourselves.

Of course, the greatest saints share God's perspective on human beings, so it's perfectly fine to tell them to just focus on people's souls. There is not much risk that somebody like Mother Theresa would fail to see somebody's unique individuality because of an excessive focus on spirituality.

But you can't believe any old blowhard neighborhood pamphleteer who claims to have a "passion for souls", if their attitude to the neighbor's kid prattling about Pokemon or something like that is indifference or contempt.

As C.S. Lewis' devil Screwtape writes:

"It is, no doubt, impossible to prevent his praying for his mother, but we have means of rendering the prayers innocuous. Make sure that they are always very 'spiritual', that is is always concerned with the state of her soul and never with her rheumatism. Two advantages will follow. In the first place, his attention will be kept on what he regards as her sins, by which, with a little guidance from you, he can be induced to mean any of her actions which are inconvenient or irritating to himself. Thus you can keep rubbing the wounds of the day a little sorer even while he is on his knees; the operation is not at all difficult and you will find it very entertaining. In the second place, since his ideas about her soul will be very crude and often erroneous, he will, in some degree, be praying for an imaginary person, and it will be your task to make that imaginary person daily less and less like the real mother—the sharp-tongued old lady at the breakfast table. In time you may get the cleavage so wide that no thought or feeling from his prayers for the imagined mother will ever flow over into his treatment of the real one. I have had patients of my own so well in hand that they could be turned at a moment's notice from impassioned prayer for a wife's or son's soul to beating or insulting the real wife or son without any qualm."

That's why evangelism is fraught with temptations and perils.  To regard ourselves as better.  To be more interested in our own (perceived) altruism and righteousness than our neighbor's actual welfare.  (Or, to take these potential pitfalls as excuses not do it at all,)  This battle is not for wusses.  If we reach out it in the face of these fears, it should normally be precisely because our friendship with the person makes us care enough about them to take a risk and share Jesus, ideally in a way that is sensitive to the person's unique interests and needs.

The article also says:

Another detrimental effect of closeness with unbelievers is our tendency to water down the truths of Scripture so as to not offend them. There are difficult truths in the Word of God, truths such as judgment and hell. When we minimize or ignore these doctrines or try to “soft pedal” them, in essence we are calling God a liar for the sake of those already in the grasp of Satan. This is not evangelism.

But being adaptive to a person's needs isn't at all the same as "soft pedalling" the gospel.  It's applying it to an actual, God-loved life.  Argh!  I think this Got Questions author thinks that liking non-Christians actually interferes with evangelism.  What could be more wrongheaded?  It's a bit like somebody who hears about someone injuring themselves at the gym, and thus decides that the healthiest lifestyle must therefore be to never exercise.

3. It's worth noting that articles like the one above are in many ways based on a spirituality of fear, especially fear by authority figures that children and young adults will fall away from the faith.  A parent or teacher who feels responsible for someone else's spiritual development is naturally tempted to be over-protective, and err on the side of caution.  But this is a trap, which prioritizes keeping people safe over obeying the will of the Father.  It blasphemously supposes that Adam is more powerful to condemn, than Christ is to save.

And it leads to the very un-Christian idea, stated quite explicitly in the first 3 sentences of the article, that spirituality is a function of our environment:

As Christians, we have to constantly face temptations and the attacks of the world around us. Everything we see, read, do, hear, put in our bodies, etc., affects us somehow. That’s why, to maintain a close relationship with God, we have to put aside our old ways of doing things—the things we watch on TV, old bad habits (excessive drinking, smoking, etc.), the activities we participate in, and the people we spend our time with.

It is not so!  "To the pure all things are pure." (Titus 1:15),  "A man is not defiled by what enters his mouth, but by what comes out of it.” (Matt 15:11).  Note how these verses DIRECTLY contradict the opening premise of the author's argument, and how this totally unbiblical idea is snuck in before ever giving Christ a chance to speak.

(That doesn't mean you should go out and destroy your body with drugs; or that God can't help you overcome harmful addictions.  But the focus of the above paragraph is entirely in the wrong place.)

Then starting in the fourth sentence, it somehow gets even worse.  The article says:

People are divided into only two categories, those who belong to the world and its ruler, Satan, and those who belong to God (Acts 26:18). These two groups of people are described in terms of opposites all through the Bible; e.g., those in darkness/those in the light; those with eternal life/those with eternal death; those who have peace with God/those who are at war with Him; those who believe the truth/those who believe the lies; those on the narrow path to salvation/those on the broad road to destruction, and many more. Clearly, the message of Scripture is that believers are completely different from nonbelievers, and it is from this perspective that we must discern what kind of friendships we can really have with unbelievers.

This is true in an eschatological sense, but note how he conveniently forgets that Jesus told us it was impossible for even the angels to make this separation into two categories prior to the Final Judgement (Matthew 13:24-30).  Still less is it possible for us human beings here on Earth to make this kind of distinction, without judging people in a way that is forbidden to us.

So this application of Scripture is amateurish at best, and diabolical at worst.

I am not saying that we should not distinguish between those inside and outside of the Church.  But any distinctions we can make between believers and unbelievers in this life must be more nuanced; allowing for more uncertainty and shades of grey, and concerned more with the qualities that are actually observable.  It is reasonable to be hopeful of the salvation of the godly Christians we know whose lives clearly exhibit humility and love (even while recognizing that it isn't our place to judge them).  On the other hand, we should be very reluctant to express a belief that even an obviously wicked person would be damned if they died in their current state.  Because this places limits on God's mercy, and exposes us to the temptation to have contempt for that person.

(I am not saying that such a person can be saved apart from Christ, since none of us are saved apart from Christ.  But I don't pretend to know all the means by which Christ can work.)

Note that the passage in Acts quoted is actually about the conversion of St. Paul, and doesn't at all prove the relevant point.  Paul was commissioned to preach the gospel "so that they may turn from darkness to light", but this did not require him to definitively know exactly which individuals he preached to were "saved" before or after his preaching.  The important thing is that Paul was working to help people be reconciled to God.

Of course, those entering the Church and being baptized should be told that they are renouncing the work of Satan and being reconciled to Christ, because (normatively speaking) that's what ought to be happening.  But this does not exclude hypocrites being falsely numbered as Christians; nor does it exclude the possibility of salvation for certain individuals known to God, who are not visible members of the Church, but are still in some kind of relation to Christ, which is not seen from the outside, and may even come as a surprise to that very person.

4. Finally, it's not the example Jesus gave us.  He was willing to make friends with sinners at parties, including types of companionship that were sufficiently intimate that they caused the Pharisees to question Jesus' own morals!

On this topic, the article you link to also abuses the Book of Proverbs:

The book of Proverbs has a few wise verses on believers befriending non-believers: "The righteous should choose his friends carefully, for the way of the wicked leads them astray" (Proverbs 12:26). We should stay away from foolish people (Proverbs 13:20, 14:7), from people who lose their temper easily (Proverbs 22:24), and from the rebellious (Proverbs 24:21). All these things represent those who have not been saved.

Uh, no.  These proverbs aren't at all about avoiding "non-believers" or the "unsaved".  First of all, that's ahistorical.  "Saved/unsaved" simply wasn't a theological category in Judaism, back when Solomon wrote Proverbs.  (For example, it wasn't until later that the concept of a final judgement and afterlife was explicitly taught by prophets.)

(There is an distinction made in the Old Testament between Israelites and foreigners.  Such passages are a bit more relevant theologically to the relationship between Christians and to those outside the Christian Church.  However, this is not the same distinction as saved/unsaved—since there's nothing in the Old Testament suggesting that all Gentiles were obliged to convert to Judaism, nor that everyone outside of the nation of Israel was automatically condemned by God.  Anyway, the Book of Proverbs does not take much notice this distinction since it is more about categorizing wise behavior in the abstract.  Indeed the word "Israel" is never used in the entire book, after the first verse!)

Secondly, as I've said, the unsaved are undetectable.  We simply can't tell whether people are unsaved by external examination, that's for God to judge.

Finally, this reading defies the literal meaning of the text.  For example, Proverbs 22:24 merely says:

Do not make friends with a hot-tempered person,
do not associate with one easily angered,

which includes many believers I regret to say!  (Conversely, there are many placid nonbelievers which are not described by this verse.)  This verse says zero, zip, nothing, about whether or not the easily angered person is "unsaved", either now or at the Final Judgement.

The reason is given in verse 25:

or you may learn their ways
and get yourself ensnared.

In other words, the goal is to avoid getting your own life caught up in grievance mongering.  There's no magic that prevents this from happening when the angry person is a fellow believer.  (And you certainly don't need to judge the other person's state of salvation to figure out whether they are causing you to get angry more often.)

And like many other proverbs, this is not even a commandment, just practical advice that may or may not be applicable to your particular situation.

Yes, it may sometimes happen that the wisest course of action is to cut off a friendship.  If your association with a specific person is dragging you down morally, without you doing them any good in return, then of course you should re-evaluate that relationship, whether or not the other person is a Christian.  (Assuming the relationship is of a purely voluntary nature, rather than e.g. a close family member, or someone you have a duty to care for.)  But this should not be done priggishly.  In such sad situations the need for separation usually arises from our own moral shortcomings; if we were more like Jesus we would be able to interact with arbitrarily bad sinners without being corrupted by them.

I do agree with the article that Christians should not marry or romantically date non-Christians.  (Although like St. Paul, I would make an exception for pre-existing relationships, since Christ came to heal, not to destroy.)  That is a different situation entirely; since marriage is a vowed, permanent one-flesh union, and there it is essential for the spouses to have union in their fundamental goals, if at all feasible.

The same would hold for any other vow of inescapable fealty to a non-Christian person or institution.  But there are not many such vows available in the modern era, besides marriage!  The medieval world was chalk full of orders of knights, monastic vows etc. while for secular moderns, marriage is pretty much the only vow-based relationship which remains.

Regarding your best friend: (1) are you helping him to become a better person than he would otherwise be?  (2) And is he helping you to become a better person than you would otherwise be?  And (3) does he know that you are a Christian, and that your faith is important to you?  If the answer to all three of these questions is yes, then you have no grounds for concern.

But, you might consider being more intentional about looking for openings to have spiritual conversations with him (unless you are already doing so), when and if the situation arises.  It doesn't need to be stereotyped or overbearing, just leaving a door open in case something develops.  The details depend a lot on the personality of your friend.  Some people live for a theological cage match, while with others you have to tread softly or you'll spook them.  You're the one who knows him, not me.  So you have to trust your own instincts, and the leading of the Spirit.

Blessings,
Aron

Posted in Ethics | 1 Comment

Christian Conscience and the Secular Workplace

by Aron Wall Posted on May 5, 2021

I had the following question from a reader [edited to make the person less identifiable, and posted with permission]:

I've been following your blog for a few months now, and I've found your posts thoughtful and gracious. Thanks for the time you put into it.

I wanted to take a minute and ask you for a line or two of your advice. I was a teacher myself for many years and realize how precious free time can be, so however brief of a response you can afford is appreciated.

Several years ago I made the transition from a more explicit ministry role to a role in the technology/media industry. I had been teaching computing for some time, was starting a family, and the financial penny eventually dropped. So I took a conversion course and made the change. My current job I view primarily as a way of supporting my role in theological education and as a part-time pastor.

The trouble is, along with the secular workplace come certain ethical grays that I hadn't been accustomed to dealing with. Seeing as you work in a secular university, I wondered if you had any thoughts on this.

For example, the net ethical consequences of the technology I work on is still TBD.  [...]  More immediately, our company provides access to an array of films, some of which are of some value, others of which are in direct opposition to the Christian values I espouse and preach.

I do have a degree of influence in the company, and have been able to steer the direction in certain positive ways during my time there. But the fact remains that impacting the nature of the entertainment industry, or influencing the ultimate societal impact of certain technologies is beyond the scope of my influence. So I will inevitably find myself earning a paycheck resulting from the promotion of certain materials that have to do with darkness rather than light.

Do I leave and protect my conscience, or remain and seek to be a light, however dimmed by the surroundings?

Peace,
______

[I wrote back something like the following:]

Peace of Christ to you as well.

It's good that you're carefully thinking through the moral consequences of your job.  I'm not going to pretend that there are always easy answers to these questions.  But maybe I can say a few things that will encourage you in your present circumstances.

1.  Jesus said we were to be "in the world, but not of the world".  It's sounds to me like you're wrestling here more with the "in" part than the "of" part.

Obviously, Christians should not directly endorse or commit acts which they think are sinful.  But when it comes to more indirect forms of enablement, I think that the Spirit of God actually leads different people to adopt different strategies, depending on the individual person.  Some Christians are called to serve God within explicitly Christian sub-communities with a relatively high degree of autonomy from secular culture, while others are called to immerse themselves within a secular culture and be salt and light there.

This isn't moral relativism.  The reason different Christians are called to different positions in society, is that it's a question of different talents and tactics; not a question of who you stand for, which always stays the same.  (There are a variety of gifts, but just one Spirit.)

2.  And sometimes, God moves people from one of these lifestyles to the other one; in other words he can call you to take different strategies at different times in your life.  St. Paul the Apostle was no stranger to this feeling of disorientation.  As he described his experience in 1 Cor 9:

Though I am free and belong to no one, I have made myself a slave to everyone, to win as many as possible.  To the Jews I became like a Jew, to win the Jews. To those under the law I became like one under the law (though I myself am not under the law), so as to win those under the law.  To those not having the law I became like one not having the law (though I am not free from God’s law but am under Christ’s law), so as to win those not having the law.  To the weak I became weak, to win the weak.  I have become all things to all people so that by all possible means I might save some.

There may be some shock of transition, in that if you started off with the "Christian sub-culture" approach, you might feel like you are compromising yourself by being involved with people or things that seem unclean to you.  (Like Peter's reaction to the sheet from heaven.)  And perhaps several of these things really are unclean, and you can't endorse them in your mind; but sometimes it's hard to separate yourself (in an external sense) from those things, without also rejecting the people involved.  That's why it's a judgement call.

The important thing is that you remain faithful to him in whatever situation he's called you to.  If you have heart-righteousness, you can't be compromised by any amount of indecency around you.  This is what St. Paul the apostle called having a "strong" faith in Romans 14-15.

No seriously, you can't be compromised by it if your heart is right.  Not if you have the kind of "innocent as doves and shrewd as serpents" character that Jesus is calling you to have.  And if you don't have that character yet, ask him for it.  He might allow you to make some mistakes along the way that are part of the learning process, but he will be faithful to you in whatever situation he's placed you into, if you place your trust in him.

3.  When I was about 6 years old, I was attending a Baptist school in Los Angeles, and I recall that they had a kids concert where my older sister helped to perform the following "Input / Output" song:

https://www.youtube.com/watch?v=whKay8FCU0I

It's cute and catchy, but I think it fundamentally contradicts Jesus teaching in Matthew 15:10-20.  Jesus says that it isn't the inputs into our life that cause us to sin, but rather the outputs (which come from our heart).  Human beings are not robots, who are mechanically controlled by our programming and data.  Attempts by Christian parents and leaders to create a "safe" environment that prevents children from ever being exposed to evil, can ironically be motivated by an almost Marxist view, where the spirit of a person is controlled by their material circumstances.  So they think that, in order to change people, you have to control them externally, rather than inspiring them from within.

It's a fear-based system (what will happen to the kids if they hear about this idea?) rather than a faith-based system.

4.  In the Old Covenant, when a ceremonially unclean object touched a clean thing, the clean thing became unclean (Haggai 2:10-14).  But in the New Covenant, there is something so perfectly clean, that when it touches an unclean thing, it is the unclean thing that becomes clean, without contaminating the clean thing (Matthew 8:1-4)!  In other words, in the Old Testament, uncleanness was contagious, but in the New Testament, cleanness is contagious, because Jesus has the power to make people clean.  And he lives inside of each Christian.  If you love as he loved, then you will be like that too.

That's why Jesus uses yeast (a reproducing organism) as a metaphor for the Kingdom of Heaven in the Gospels.  (Even though in the Old Testament Passover ritual, yeast had previously been used as a metaphor for sin, again because of its contagiousness.)

The reason uncleanness was contagious in the Old Covenant was that there hadn't yet come into the world a powerful enough love and light and disinfectant to fully cleanse our sin.  So God gave Israel some quarantine rules, as a temporary measure, until Christ entered the world to save it.  But after Christ came, these quarantine rules were no longer so necessary.

That's why Jesus went to dinner parties with prostitutes and tax collectors.  You can be pretty sure that some stuff happened at those parties that you and I would not approve of.  But the Son of Man went to them anyways, to seek and save that which was lost.

Like I said, some people are called to live in Christian sub-cultures, and I'm not in any way trying to minimize or disrespect that choice, since it works well for many people.  But sometimes people conceive of such subcultures wrongly, as a place where we can go to avoid temptations.  But that's just not possible in this life!  A Christian sub-culture just exposes you to a different set of possible temptations.  (Such as the temptation to slap the word "Christian" on schools or music, and assume they've just been redeemed, even though nothing in people's hearts is any different than what happens outside in the "world".)

Don't get me wrong, an unclean thing can still infect you today, if you turn from Christ and your heart lusts after it.  Christians must keep themselves pure from worldly desires (James 4:4, Rev 18:4).  Yet Jesus taught his apostles that the dividing line of purity has to be in the heart, not in walls of separation from other people.  As the famous quotation from St. Solzhenitsyn goes:

Gradually it was disclosed to me that the line separating good and evil passes not through states, nor between classes, nor between political parties either—but right through every human heart—and through all human hearts.

If you work in a secular environment, there may be tendencies for it to look a little bit like Romans chapter 1.  But if you work in a churchy environment, there will be temptations for you to become like Romans chapter 2; and these temptations can sometimes be very subtle, difficult to avoid, and encouraged by the community.  Neither way looks very much like Romans chapter 8, which is where we ought to be living.  If so, we can triumphantly say:

"For I am persuaded, that neither death, nor life, nor angels, nor principalities, nor powers, nor things present, nor things to come, nor height, nor depth, nor [secular culture nor religious culture], shall be able to separate us from the love of God, which is in Christ Jesus our Lord."

5. Your metaphor of "light dimmed by the surroundings" is not really sound.  Darkness is just the absence of light, and hence it has no inherent power of its own to overcome light (John 1:5).

This is certainly true for literal light.  Darkness is not a substance.  There is no such thing as a "dark flashlight" which can emit darkness the way a normal flashlight produces light.  Only if the light is concealed or blocked by an opaque object (so that the light doesn't reach whatever spot you are looking at) can there be darkness somewhere.  And even when the light is blocked by a solid object, it still shines on whatever object is blocking it, and illuminates it.

The light of God is truth.  Do you believe that truth is more powerful than lies?  Do you really believe it?

6.  Reread the Parable of the Wheat and the Tares in Matt 13:24-30.

Part of the point of this story is that no person is smart enough to separate the wheat from the tares; at least, not right now at this stage in history.  (The separation is coming, but this has to wait for the final judgment, when both plants have reached their full maturity.)

You might think you know which movies are "wheat" and which ones are "tares", but art is a funny thing because it can speak to people's hearts in ways that aren't entirely predictable.  It is good that there exist stories of every possible sort, since they enlarge the range of our thinking about the world.

Most of the divines of St. William Shakespeare's day thought it was a sin to attend theatrical performances, because of their ribaldry and because it distracted people from more noble endeavors, but today he is considered "high culture".  Can you imagine where the English language would be, without Hamlet and his other plays?  We can all express our thoughts more vividly, because he existed.

One certainly cannot judge the spiritual value of a work by applying superficial "content filters" (e.g. if the movie depicts adultery or swearing or smoking or gang warfare or alternative sexualities, then it is bad; if it avoids all this stuff and also has an uplifting overall message, then it is good).

There are some deeply spiritual and moral works of literature which portray people committing crimes or serious sins, but they are still wholesome precisely because they shine a light on how this actually affects real people.  As a result of seeing these consequences more clearly, people can be inspired to turn away from destructive actions before they ruin their lives.  Indeed, in some ways it's especially important to have stories portraying sinful deeds, since that's the only possible way for us to learn about sin, without having to actually commit it.

Then there are films and novels that are deeply anti-Christian in their outlook (I'm not talking about straight up XXX pornography here, but rather works which have some artistic merits, but also glorify ungodly values).   Even so, that doesn't automatically imply that it is only bad for the world that they exist.  It could well be that some of these stories help the discerning to see something new about the world, and some might even be the instrument of somebody's conversion to Christ!  After all, I don't think any work can have much artistic value if it doesn't resonate with some important truth about the world (even if that truth might be mixed with lies, in a way that is a trap for the unwary).  And to the extent a work of fiction resonates with any truth, it reveals something about God who is the Truth—even if the person who wrote it is an atheist and never intended for that to happen.

Conversely, a studio which makes a film that is "clean" and "Christian" might still be creating a work with very little artistic value.  Because artistic value is closely connected to truth, this implies that it is (to some degree) telling lies about what humans are like, and what real virtue and vice look like.  Such fiction specializes in equipping people to see the world in an immature and unrealistic manner.  There's a whole Christian film industry which specializes in this type of glop.  (Of course there are also some great Christian films like Chariots of Fire.)

So maybe some of the works which seem to us like "wheat" are actually "tares", or vice versa!  It's not really our place to judge.  (Of course it is fine to judge for yourself what seems spiritually/artistically good, for purposes of deciding what you will watch, or make, or recommend to your friends!  What I mean by "not judging" is more that if somebody else makes something on your platform, and then somebody else enjoys it, you aren't necessarily in a good position to know whether it will have been good or bad for them, in the long run.)

7.  Suppose now that you are a creator of technology.  You can foresee that this technology will be used to produce both good things and bad things.  Some will use it to become more virtuous, while others will use it to sin.  What should you do?

It seems to me you have a pretty obvious role-model here.  I'm talking about God himself.  He created a world, and he could have turned on content filters that made it so bad things weren't possible.  But in his wisdom, he didn't do that.  Instead he put all sorts of things in the world that humans can use both for good purposes and for bad purposes, and he gives us the freedom and space to pick what we will do with them.  Most of the time, he lets people make their own mistakes and learn from them, so we can learn the consequences for ourselves.  Of course, he's provided us with lots of direction and guidance in the Bible, and yet he doesn't even force people to believe he exists, if they don't want to do that!  Yet even so he still provides the same sunshine and rain for the wicked, just as much as to the righteous (Matt 5:45).

As my Dad said in an interview once about the philosophy that motivated him to make the Perl programming language:

The philosophy of TMTOWTDI ("There's more than one way to do it.") is a direct result of observing that the Author of the universe is humble, and chooses to exercise control in subtle rather than in heavy-handed ways. The universe doesn't come with enforced style guidelines. Creative people will develop style on their own. Those are the sort of people that will make heaven a nice place.

8.  New technology often has unforeseen consequences, and can drive social change.  But once again the character of the heart matters more than the nature of the particular medium.

Historically you can find alarmists whenever any new communications media appears (e.g. people freaked out about the printing press, and about radio, and about TV, and about the internet, and about smart phones).  And there have always been people who consumed each of these products in an unhealthy and addicted manner, or were led astray by lies.  But when the dust settles, we've usually found that the essentials of human life are still the same under new technological conditions.

Even in the days of Twitter, print books still exist, and a lot of people still read them.  Or if, someday in the future, Virtual Reality reaches the mass market, it will just be one more thing in the media ecosystem.  People will still meet in person and talk to each other (once the pandemic ends, anyway!)

9.  Before Jesus preached the gospel, he made furniture.  A skilled craftsman has to judge whether they are making good, solid, reliable work.  Whether it is useful to others.  Some people might have used his furniture in morally questionable ways, but a craftsman can't prevent that.  He can only make the best product he can, and leave the rest to the customer.

So if you think whatever you make personally is good in and of itself, and that it will be mostly used in good ways, then I think your job is morally justifiable.  Even if some folks take advantage of the opportunity to sin.  If, however, you think that the evil predominates (e.g. if you were making your money as a loan-shark exploiting poor people) then you'd need to find another line of work.

10.  If I had interpreted 2 Cor 6:14 with excessive rigor, I could never have become a physicist working in my area of interest (my PhD advisor isn't a Christian, and virtually all of the top universities are secular in practice, if not always in theory).  But the rest of St. Paul's writings make it abundantly clear that he never meant that we shouldn't interact with non-Christians socially or in the marketplace.

I don't think working in a secular workplace contradicts this passage, as long as you keep open the option to leave, in the event that you would otherwise be forced to cross a line which violates your own conscience.

I think it is of enormous importance that this line of conscience exists (that it is clear in your own mind, and that your coworkers know there are some things you would never do).  But it is actually not very important for all Christians to draw this line in exactly the same place as each other.  And it's also not wrong to think strategically—in light of your specific circumstances and culture—when you decide exactly where this boundary should be, based on the truths that you think are the most important to witness to.

Refusing to do specific things for specific moral reasons, seems like a far more compelling testimony to outsiders, then simply refusing to associate with them from the outset would be.  Even non-believers often respect and admire people with a strong internal moral compass, as long as they don't come across as judgemental.

(Of course if God makes it clear to you that he's drawing a line you for you in some particular place, then obviously follow the Spirit's prompting, however difficult it may be.  But in such cases there's no need for my advice.)

I can't make this judgement call for you.  But I don't think the situation you've outlined for me is necessarily an ungodly compromise.  Maybe it's exactly where God wants you to be, and you just need to approach the situation with faith, rather than doubting.

Blessings,
Aron

Posted in Ethics | 4 Comments