Part 1: Introducing Black Holes
Part 2: Thermodynamics of Regular Stuff
Part 3: Thermodynamics of Black Holes
Actually, it was Galileo who first discovered the Principle of Relativity (though he didn't call it that). What Einstein did was show how the Principle of Relativity could be consistent with a world in which light always travels at the same speed (in a vacuum) no matter what. In order to reconcile these two ideas there have to be all sorts of counterintuitive effects in which moving objects experience time dilation and length contraction. In a nutshell, measurements of space and time depend on the measuring device's speed.
In Special Relativity, spacetime also comes with a notion of ``causality'' (i.e. rules of cause and effect): there are restrictions on which things can affect which other things. In particular, no information can travel faster than the speed of light in the vacuum `c' (about 3 x 10^8 meters per second). (Perhaps this special speed c really ought to be called the maximum speed of information. After all, light slows down when it travels through a physical medium, such as water, but in Special Relativity that doesn't affect c which is still 3 x 10^8 m/s).
Another well-known implication of Special Relativity is the equivalence of mass m and energy E. It's expressed with the most famous equation of all time, but since you already know that equation, and I promised not to include any equations, I won't write it down here.
I could go into more detail, but there's lots of good popularized descriptions of Special Relativity on the web; the main reason I'm mentioning Special Relativity is so you won't confuse it with an even bigger, badder theory of Einstein's about spacetime: General Relativity. The philosophical implications of Special Relativity are small peas compared to General Relativity. In Special Relativity, space and time behave in a weird way, but that way is fixed once and for all. Spacetime is still what's called a ``background structure'', meaning that it affects the rest of the world but isn't affected by it. It's just the stage on which the play is performed, not an actor in the play itself. (Okay, that was one trite metaphor. I'll try to avoid doing it again).
For example, time travels slightly slower near a massive body like the Earth. Time runs about one part in a billion times slower on the surface of the earth than it does in outer space! This effect may seem exceedingly small, but it is actually the reason why things fall down. You see, there's this ``Principle of Least Action'' which states that objects fall in gravitational fields in such a way as to maximize the total amount of time experienced by the object when travelling between its beginning and ending positions.
For example, suppose you fling a rock way up into the air and catch it exactly 10 seconds later. (That's 10 seconds as measured by your watch.) What trajectory will maximize the amount of time the rock experiences? This involves a tradeoff between special and General Relativity effects. On the one hand, the rock ``wants'' to get as high as possible during its journey, in order to get farther away from the Earth, where time runs faster. On the other hand, if it goes too fast in its ascent and descent, it will be slowed down due to special relativistic time dilation of moving objects. It turns out that the path the rock actually takes (ignoring air resistance) is exactly the path which maximizes the total amount of time spent in transit!
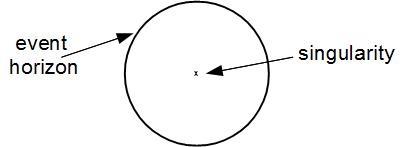
If you concentrate enough mass into the same region of space, then the distortion of spacetime is so severe that you can get a region which cannot affect the outside world. Things can fall in, but they can't come out again. This region of space is called a black hole. Here is a picture of a simple (nonrotating, noncharged) black hole sitting in empty space:

Warnings: This diagram represents space at one time. However, the meaning of ``at one time'' is highly ambiguous in General Relativity and needs to be made precise by choosing a set of coordinates, which has not been done. Distances and travel times are not, and cannot be, adequately represented by the Euclidean distances found on your computer monitor. The diagram is a two dimensional representation of a three dimensional object—the user should pretend that the circle is actually a sphere. THIS DIAGRAM IS NOT INTENDED FOR USE IN NAVIGATION; PRODUCT IS PROVIDED ``AS IS'' WITH NO EXPRESS OR IMPLIED WARRANTY. Please consult a real General Relativity textbook for more information.
The event horizon of a black hole is the surface where, if you fall across it, it is impossible to ever escape again to the outside world. That is because, from the perspective of someone falling across, the event horizon is moving outward at the speed of light (even though it doesn't grow in size). In the case of a nonrotating black hole, the event horizon is spherical in shape. If you're worried about falling into black holes, you may want to know: Just how big is a black hole? And the answer is: It depends. A black hole can be of any size. The radius of a black hole is proportional to the mass of the black hole: the more mass a black hole gets, the bigger it gets. If the sun were to collapse into a black hole (don't worry, it can't) the radius would be about 3 km (much smaller than the sun's current radius of 700,000 km). If this impossible event were to occur, The earth's orbit would not change! That is because the gravitational acceleration towards an object depends only on its mass and the distance. Black holes have no more ``sucking power'' than anything else of the same mass. It's just that the mass is more concentrated.
Although the event horizon is a special place from the perspective of causality, you shouldn't think of it as an actual physical object sitting there in space. If you fell across the event horizon, you wouldn't hit any object as you crossed; it's just empty space. If you look really closely at a point on the event horizon, it would look just like anywhere else in the universe. It's only special from the perspective of the whole spacetime.
If you did fall across the horizon, you would be inevitably sucked further and further in to the center of the black hole. There you would be squashed into the singularity. From the perspective of General Relativity, the distortions of space and time become infinite at the singularity. Since it makes no sense to ask what happens after you hit the singularity, as far as General Relativity in concerned, time comes to an end at the singularity of the black hole. (This is similar to the way time seems to have come into existence in the first place, with the ``Big Bang'' singularity. However, it is also different in that the Big Bang seems to have started time everywhere at once, whereas black hole singularities only end time in one place.)
On the other hand, General Relativity doesn't take into account quantum mechanics. Once one gets close enough to the singularity, quantum mechanical uncertainty in the geometry of space and time ought to become important. Since we don't really know how to make mathematically consistent theories of quantum gravitation, a better answer is that we don't know what really happens right at the singularity. It could be, as some have suggested, that the singularity would be resolved somehow into a portal to some other region of spacetime (perhaps a ``baby universe''). But suggestions like this are all highly speculative. (I myself have argued in one of my published papers that time really does end at the singularity, but of course I don't really know for sure, any more than anyone else does.)
You might say, so now that we've been introduced to black holes, what about their thermodynamics? It's nice that you're so eager to learn about my work. Unfortunately, before we can discuss the thermodynamics of black holes, I'm going to have to bring you up to speed on plain old ordinary thermodynamics first.

At any time, the beverage is in a particular state of being. Its state can be described by a bunch of properties such as volume, pressure, and chemical composition. But the properties which are most important in thermodynamics are the energy, the entropy, and the temperature.
``But what is energy?'' you might ask. The most insightful description I can give in a hurry is this: energy is momentum in the time direction. Einstein taught us with his theory of Special Relativity that time is a dimension, which should be treated similarly to space. This leads to a sort of non-discrimination principle in physics: for any very-important conserved quantity which points in a spatial direction (such as momentum) there has to be a corresponding very-important quantity which points in the time direction.
There's a famous theorem in physics proven by a mathematician named Emmy Noether. She showed that for any symmetry in physics, there's always a corresponding quantity which is conserved. For example, the laws of physics have spatial translation symmetry: they are the same in all places. This implies that momentum is conserved. The laws of physics also have time translation symmetry: they are the same at all times. This implies that energy is conserved.
Still confused about what energy is? That's okay. In order to understand what's coming, you don't need to know anything about the energy other than that it's conserved. It also helps to know that things moving around faster tend to have more energy than things moving slower, all other things being equal. If you're willing to take it on faith that there is indeed such a thing as energy, keep reading!
So far I've been talking about entropy almost as though it were a physical substance, but that isn't quite right. It's really about the statistics of the atoms in the substance. People who write popularized physics textbooks sometimes call it the amount of disorder, but I find that most people are confused by that phrase; states with high entropy (like a box of gas) can seem very ordered and uniform to human beings. A better way to think about it is this:
Entropy is a number which counts the total number of possible ways for the atoms in an object to be arranged.
Let's discuss this in terms of our mug of addictive beverage. There are lots of different ways that the atoms could be arranged in your favorite beverage such that it would look and taste just the same to you at a macroscopic scale. Since atoms are really tiny, there are a huge number of possible ways. But the total number of ways is finite, since there are a finite number of atoms in the beverage.
(You might have thought that there are actually an infinite number of possible configurations since each atom can have any position in space, and space is continuous. But this is not so because of quantum mechanics. Heisenberg's Uncertainty Principle says that the more accurately you measure the position of an atom, the less accurately its momentum can be determined. This means that effectively there are only a finite number of configurations which can be distinguished from each other. In order to measure the positions of the beverage atoms more accurately, we would have to increase the uncertainty in the momentum, which would mean the atoms would be flying around faster on average, which would require adding energy to the system to heat it up.)
I've made one small simplification in the definition of the entropy. Physicists usually define the entropy a little differently that what I've done above, as the logarithm of the total number of ways for the system to be. Don't panic if you don't know what a logarithm is, since it's not very important to understanding the basic meaning of the entropy. Instead let me explain why the physicists added in this unpleasant extra wrinkle. Suppose we have two different systems: say a mug of coffee on the left and a mug of tea on the right:


There is a total number of ways for the atoms in the tea molecules to be arranged, and there is also a total number of ways for the atoms in the coffee molecules to be arranged. But suppose we are interested in the combined system which contains the tea AND the coffee. How many ways are there for the atoms in this system to be arranged? It turns out to be the number of ways for the tea to be arranged times the number of ways for the coffee to be arranged. But this times business is kind of ugly; it messes up the narrative in which we can think of the entropy as being like a substance which can be added up. For example, the total energy of the mugs is the energy of the left mug plus the energy in the right mug. We want entropy to work the same way, so that the entropy of both mugs is the sum of the entropy in each mug. Now, the logarithm is just a clever function math people came up with that turns multiplication problems into addition problems. That's why we define the entropy as the logarithm of the number of configurations.
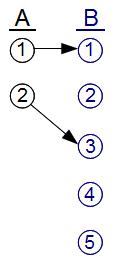
Let's label the first set of ``microstates'' A1 and A2, and the second set B1 through B5, for a total of 7 microstates. Because there are more ways for B to be arranged than A, B has the higher entropy.
Now suppose we prepare a system in state A, the lower entropy state. In reality, of course, the atoms of A have to be arranged in a specific configuration, either A1 or A2. But since we have no idea which of the two microstates it is, if we prepare the system in state A, we should really think of it as having a 1/2 probability to be in each of the 2 microstates. (If we did know something about which microstate it was in, this information should have been included in the macrostate.) Similarly, if we prepare a system in macrostate B, it should have a 1/5 chance to be in each of the five microstates B1 through B5.
Now we know that as time passes, things evolve. (Unlike biologists, who use the word ``evolution'' to describe the change of species with time, physicists use the word evolution to refer to changes in anything as time passes.) For example, if we prepare the system in state A, wait one minute, and then check up on it, we might find that the system has changed into state B. This would be an entropy increasing process. Or we might prepare the system in state B, and then check to see if it has changed into state A. That would be an entropy decreasing process. But are both of these possible?
The key is to realize that in any transition of a system from one macrostate to another macrostate, each microstate needs to have a consistent, distinct history. States which are distinct at one time must remain distinct for all times. So if after one minute, state A1 evolves into, e.g. B1, then state A2 couldn't also evolve into state B1, it would have to evolve into some other state (such as B2). Different timelines can't merge into each other. Another way to put this is that at the atomic scale, the laws of physics are ``reversible'': not only can you predict the future from the past, you can also predict the past from the future.
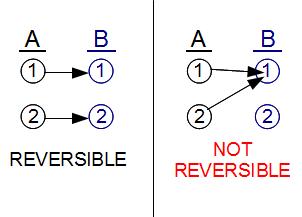
(In order to keep things simple, I've been talking as though the laws of physics are deterministic, so that A1 would evolve to B1 with 100% probability. You might have read that quantum mechanics is not deterministic, meaning that in quantum mechanics there is a fundamental role for chance or probability. For example, maybe after one minute, state A1 would have an 83% probability to evolve to B1, a 12% chance to evolve to B2, and a 5% chance to evolve to some other state. Even though I've used quantum mechanics to argue that there are only a finite number of possible atomic configurations, I'm going to ignore this complication and assume that time evolution is deterministic. However, one gets the same answer when one takes quantum mechanics into account. The key point is that even though quantum mechanics is indeterministic, it turns out to still be reversible: one can predict the past from the future probabilistically, in the same sense that one can predict the future from the past. (That the laws of physics are both probabilistic AND reversible is one of those bizarre paradoxes of quantum mechanics; understanding how both properties are compatible would require discussing crazy things like quantum superpositions and interference—which I don't have time for here.))
Ironically, the fact that the evolution of matter is reversible on the atomic scale turns out to imply that there are irreversible, one-way processes at macroscopic human sized scales. The laws of physics can change lower entropy macrostates into higher entropy macrostates, but not vice versa. But don't take my word for this: we'll check it right now for the example macrostates A and B (which have 2 and 5 microstates respectively). The only thing we'll assume about the laws of physics is that they are reversible.
The laws of physics might conceivably say that A must evolve into B, because B has more microstates. There are enough possible microstates in B, that each microstate in A can evolve into a different microstate in B. Since in this example, I haven't actually told you what the laws of physics are, we can't know for sure that A will evolve into B. But it's logically possible that A could evolve into B, since there's no conflict with reversibility. For example:
On the other hand, the laws of physics CANNOT say that B will evolve into A, because there are not enough distinct microstates of A. The best that could happen is that 2 out of the 5 possible B microstates might evolve into A microstates, while the remaining 3 states would either remain in the B macrostate, or perhaps turn into some other macrostate C. Because the ratio of microstates is 2:5, the probability of evolution from B to A can be at most 2/5.
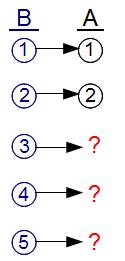
So it actually is possible for the entropy to decrease, it's just less likely than entropy increasing processes. This makes the Second Law of thermodynamics what's called a statistical law, meaning it holds on average, but can sometimes be violated in individual cases. (Even if the laws of physics were deterministic, we would still have to use probabilities in thermodynamics. This is not a fundamental uncertainty like in quantum mechanics. Instead the uncertainty comes from our practical inability to track the exact positions of every atom in a material substance.)
You may say, 2/5 isn't that small of a probability for something to happen. But in real life examples, the ratios of microstates tend to be much, much huger than 2:5. We're talking about gigantic probability ratios like 1:10^(10^25). So the probability that the entropy will decrease by a noticable macroscopic amount is so small that for all practical purposes one might as well treat it as impossible. This is why the Second Law is usually stated in an absolute form: the total entropy of a closed system cannot decrease as time passes.
The Second Law of thermodynamics accounts for all the irreversible processes we see on a day to day basis, such as eggs breaking, rain falling, and friction slowing things down and heating things up. For almost any physical process you can think of that only happens in one direction, it's because the final state has more entropy than the initial state. It's what makes the past different from the future. For reasons not currently understood by scientists, the universe started out in a very low entropy state. Given this unexplained initial condition, the Second Law says that the universe will produce more and more entropy until eventually it reaches whatever state has the maximum possible entropy, in which no more one-way processes (like life) can occur.
People often give the Second Law a bad rap because of this life-ending conclusion. But you shouldn't think of entropy as being intrinsically evil. It's true that the increase of entropy guarantees that we are all going to die one day (though I imagine most of us will perish long before the heat death of the universe). But remember that without entropy increase there wouldn't be birth, growth, perception, or memory. All of these are one-way processes without which we could not exist.
In every day speech, we use the terms ``heat'' and ``hot temperature'' roughly interchangeably, but in physics heat and temperature mean two different, but related, things. Heat just means the the amount of energy which is stored in the motion of atoms at the microscopic scale. When the atoms an object is made out of are all moving in the same direction, then the object itself is in motion, and has kinetic energy. But when the atoms in an object are moving in random different directions, the object looks like it's standing still macroscopically even though there may be lots of kinetic energy in the individual atoms. That kind of random energy is called heat. In the case of a liquid or a gas, the heat comes because the molecules are flying around in lots of different directions. In the case of a solid, the atoms are stuck in a fixed pattern, but they can still jiggle around back and forth a little. Either way, we call the energy stored in the atoms of a substance by the name heat.
One can see just from this that heat doesn't mean the same thing as temperature. Consider once again the two mugs of alluring beverage:


This time let's say both mugs are identical. Since heat is just a kind of thing (energy) stored in the mugs, obviously there's got to be twice as much heat stored in two mugs, as there is heat stored in one mug. But it doesn't work that way for temperature. If one mug has a temperature of 300 degrees above absolute zero, it's not true that both mugs together have a temperature of 600 degrees. Temperature doesn't work that way. (In physics language, we call a quantity ``extensive'' if you can find out the total amount in an object by adding up the amounts in all of the object's parts. Mass, energy, and entropy are all extensive quantities. The temperature, however, is an ``intensive'' quantity, meaning that it represents a quality which is equally present in each part of the system.)
So if heat is energy, what is the temperature? It turns out that you can define temperature in terms of the energy and entropy of a system. It is defined as follows:
The temperature of an object is proportional to the amount of heat it takes to raise the entropy of that object by a given small amount.
Remember that the entropy counts the total number of ways for a system to be, and that this count is finite because there is only a limited amount of energy available in the system. In most systems, if you increase the amount of heat energy in the system, the atoms will start flying around faster, and this will increase the number of possible ways for the atoms to be arranged. So in order to increase the entropy a little bit, the energy has to increase too by a little bit. The question is, how much energy do you need per unit of entropy?
In a system with high temperature, it takes a lot of energy to raise the entropy by a unit amount. In a system with low temperature, it takes only a little bit of energy to raise the entropy by a unit amount. This relationship between energy, entropy, and temperature is known as the Clausius relation, after a German scientist named Rudolph Clausius, who first introduced the idea of entropy. (This was before anyone knew that entropy counted possible configurations of atoms. Instead, he defined the entropy in terms of temperature and heat by using the Clausius relation.)
When we put the Clausius relation together with the First and Second Law of thermodynamics, one can derive a profound conclusion:
Heat always flows from hotter objects to colder objects, never vice versa.
Of course, we already know from our personal experience. The exciting thing is that we can prove it HAD to be that way from first principles. The proof is simple: By the First Law of thermodynamics, energy is conserved. That means that heat can't come from nowhere: if it leaves one object it has to go to the other object, and vice versa. By the Second Law of thermodynamics, entropy has to increase, not decrease. But the Clausius relation says that energy is more efficiently used to produce entropy in the colder object than the hotter object. That means that the entropy will increase if energy flows from the hotter object to the colder one.
This is why, if you leave a mug of hot beverage on the table, it will eventually cool down to room temperature. It is because there are an astronomically huger number of ways for the room to be when the heat is distributed more equally. The random interactions between the beverage and its surroundings are therefore each more likely to cool the beverage down than to heat it up.
Even if the mug weren't actually touching any other objects, it would still eventually reach room temperature, by radiating photons (particles of light) out from its edges. (You've probably heard already that quantum mechanics, particles and waves are the same thing, so hopefully you won't be too shocked to hear me talk about ``wavelengths'' of particles.) All hot objects radiate these photons, but at room temperature these photons of ``heat radiation'' are in the infrared wavelengths where we can't see them (though sometimes we can feel them). That's why most things don't glow in the dark. However, when things get hotter they start emitting radiation in shorter and shorter wavelengths. That's why if you heat something up hot enough, it becomes first ``red hot'' and then ``white hot'', as the photons include first red, and then the whole visible spectrum of wavelengths.
No, the surprise is that black holes—or more specifically their event horizons—obey the same laws of thermodynamics as regular objects, even though it seems like they shouldn't! In particular, the horizon, in its interactions with the rest of the universe (stuff outside the event horizon) seems to obey the First Law (energy conservation), the Second Law (entropy increase), as well as the Clausius relationship between energy, entropy, and temperature.
This is strange, because normally these laws of thermodynamics only apply to a closed system, that does not interact with the rest of the universe. (For example, the energy of the whole universe is conserved, but the energy of an individual part of the universe is not conserved, since energy can be transferred from one object to another. Similarly, the entropy of the whole universe has to go up, but entropy can be transferred from one system to another.) In General Relativity, the outside of the black hole is NOT a closed system. That is because stuff can fall into the black hole and disappear. Nevertheless, the black hole obeys the laws of thermodynamics, without worrying about what's inside the event horizon.
Let's look at this in more detail:
So you might think that the energy which falls into black holes is effectively lost forever. But you would be wrong. The reason is gravity. You can tell how much energy (or mass) a black hole has without jumping in by measuring it's gravitational field. For example, you could put a satellite in orbit very far away from the black hole, and measure the total mass of the black hole by measuring how much gravity is exerted on that satellite.
This is the answer to the question people sometimes ask ``If nothing can escape from a black hole, how can the gravity escape from the black hole?'' The answer is that the gravitational field was never trapped in the black hole in the first place. Gravity is a distortion of spacetime which extends out from any object with mass, going all the way out to infinity. You can tell how much mass is present from very, very far away. No matter what happens to the mass on the inside, the gravitational field far from the black hole just stays the same.
Therefore, energy is conserved even outside of the black hole, without reference to anything that happens on the inside. This is the First Law of thermodynamics as applied to black holes.
It might seem like a black hole should be considered to have a temperature of absolute zero. The definition of the black hole is that stuff can only fall in, it can't escape. This suggests that in any interaction with something else (such as a whirling disk of plasma spiraling around the black hole) heat can flow into the black hole, but not out of it. Since heat always flows from the hotter object to the colder object, it seems like a black hole has to be as cold as possible. In other words, absolute zero.
This argument turns out to be completely correct if you ignore quantum mechanical effects. However, if you take into account quantum mechanics, it turns out black holes do emit radiation into empty space, just like any other object with a temperature. This is called ``Hawking radiation'' after Stephen Hawking who first calculated it. The temperature of the radiation coming out can then be thought of as the temperature of the black hole.
How is it possible for this Hawking radiation to escape the black hole? After all, nothing can escape past the event horizon. The answer is that this radiation was never stored inside the horizon to begin with. It actually comes from just outside the event horizon. If you zoom in really close to the event horizon, you would see that right at the event horizon, there are particles of every sort there.
Actually, that's true if you zoom in on any point anywhere in the universe, not just near the event horizon. Even in empty space these so-called ``virtual'' particles exist, temporarily popping into existence and then disappearing again. That's because the vacuum is defined as the state which has the lowest possible energy, not a state in which no particles exist. In fact there are infinitely many different particles of every kind in the vacuum. The closer you look, the more you would see.
So in this respect, the event horizon isn't different from anywhere else. What's special about the event horizon is a certain sort of ``stretching'' effect occurs. Particles just slightly outside of the event horizon can escape the black hole (if they are going fast enough outwards), while particles just slightly inside have to fall in and hit the singularity. So virtual particles which start out being very close end up being separated. At the same time, the ``wavelength'' of the particles gets stretched out too. Particles with arbitrarily tiny wavelengths, scrunched very close to the horizon, end up being stretched out to wavelengths of roughly the same length as the radius of the black hole.
How hot is the black hole? It depends. The bigger a black hole is, the longer the wavelength of the photons coming out. That corresponds to a lower temperature. For the 3 km black hole with the mass of the sun, the photons are radio waves. That corresponds to 6 x 10^(-9) °C above absolute zero, which is way too cold to have any chance to measure the Hawking radiation. Thus, although we have good observational evidence for the existence of black holes, the Hawking radiation is purely theoretical right now. The only way we would have any chance of observing it is if we found some way to manufacture or discover a much smaller (and therefore hotter) black hole.
The entropy of a black hole is proportional to the surface area of its event horizon.
So bigger black holes have more entropy. But does this entropy really behave like the entropy of an ordinary system? If so, it should obey the Second Law of thermodynamics: the entropy should always increase as time passes. For a black hole, this becomes the ``Generalized Second Law'' of black hole thermodynamics:
The area of a black hole event horizon, plus the entropy of any stuff outside of the event horizon, cannot decrease as time passes.
In order to see whether this is true, physicists have tried to imagine all sorts of scenarios in which the entropy might decrease. But no matter how hard they try, it always seems like it always increases. For example, if you dump something with entropy into the black hole, the entropy outside the event horizon goes down. But the stuff always carries energy into the black hole, and eating energy makes the black hole grow bigger. The resulting increase in the area of the event horizon is always big enough to make the total entropy go up.
On the other hand, if you put a black hole into empty space, it will lose energy through Hawking radiation. This makes the black hole shrink, and lose entropy. However, the Hawking radiation leaving the black hole itself contains entropy (because there's lots of different possible configurations for the outgoing radiation). Once again, the total entropy increases.
It used to be that we didn't understand the thermodynamics of ordinary stuff either. That was because thermodynamics was discovered before the atomic theory. Once scientists realized that matter was made out of atoms, they figured out why the Second Law of thermodynamics was true.
In General Relativity, a black hole is a very simple object. If you know the mass of a black hole, and how fast it is spinning, you know everything about the black hole. But if black holes actually carry a huge amount of entropy, it seems like there has to be some sort of object whose possible configurations we are counting. Thing is, though, the black hole isn't made out of ordinary stuff, it's made out of pure gravity. And gravity is just distortions in space and time. So it seems like in order to understand why black holes have entropy, we would need something like an atomic theory of spacetime.
In order to account for the entropy of a black hole, we would need to figure out what spacetime itself is made out of. Just like matter is made out of little tiny bits called atoms, which account for its thermodynamical properties, maybe spacetime is made out of even tinier little ``chunks'' of some sort. The entropy of the black hole would come from counting the number of ways for these unknown structures to be arranged. Even though space and time look continuous, that could just be because the things it is made out of are so small that you can't see them individually, so spacetime looks smooth at human scales. That's what black hole entropy seems to suggest, anyway.
We think this ``atomic theory'' of spacetime probably occurs at distance scales of about 10^(-35) meters. That's about 20 orders of magnitude smaller than the size of a proton or neutron. It's much, much, much smaller than anything that particle physicists are able to measure experimentally in the laboratory. This is the scale of ``quantum gravity'', where the energy flows due to virtual particles become so great that our concepts of spacetime break down. No one knows what spacetime looks like on these scales, and we have very little in the way of experimental clues.
That's why black hole thermodynamics is so important, because it provides hints about the behavior of whatever it is space and time are made out of. Can we find a theory of discrete spacetime which explains how big the entropy is? Why is it proportional to the area? (In most substances, the entropy is proportional to the volume.) Why does it increase? Why should spacetime behave like a continuum on large distance scales despite all this strange stuff happening at short distances? These challenging questions are goalposts for a yet-to-be-formulated theory of what the world is made out of.
Aron Wall's Homepage
Go to Top
You can email me by using my first name, followed by my last name, followed by umd.edu (a***w***@umd.edu).